17.1.2勾股定理的应用练习
图片预览
文档简介
登陆21世纪教育 助您教考全无忧
《勾股定理》练习
一、选择——基础知识运用
1.同一平面内有A、B、C三点,A、B两点相距5cm,点C到直线AB的距离为2cm,且△ABC为直角三角形,则满足上述条件的点C有( )21·cn·jy·com
A. 2个
B. 4个
C. 6个
D. 8个
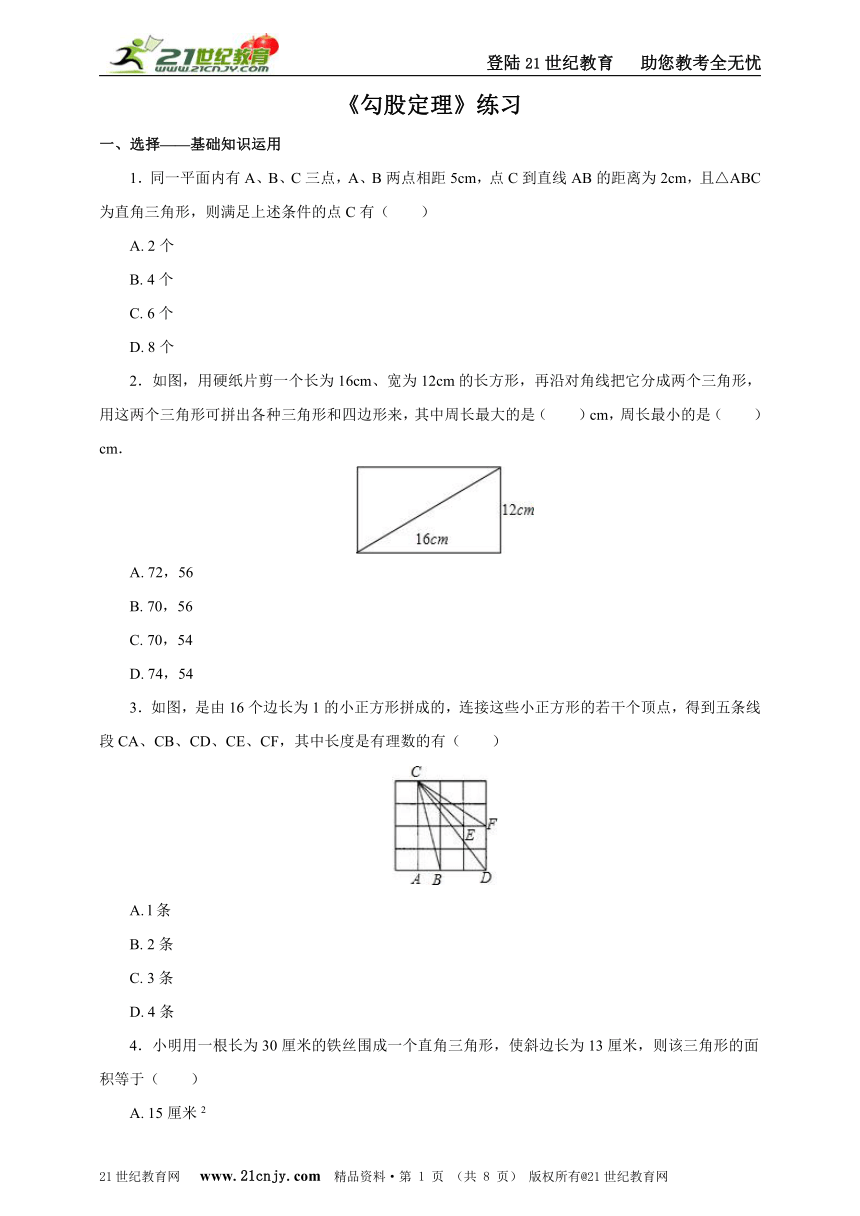
2.如图,用硬纸片剪一个长为16cm、宽 ( http: / / www.21cnjy.com )为12cm的长方形,再沿对角线把它分成两个三角形,用这两个三角形可拼出各种三角形和四边形来,其中周长最大的是( )cm,周长最小的是( )cm.21世纪教育网版权所有
( http: / / www.21cnjy.com / )
A. 72,56
B. 70,56
C. 70,54
D. 74,54
3.如图,是由16个边长为1的小正方形拼成 ( http: / / www.21cnjy.com )的,连接这些小正方形的若干个顶点,得到五条线段CA、CB、CD、CE、CF,其中长度是有理数的有( )2·1·c·n·j·y
( http: / / www.21cnjy.com / )
A. l条
B. 2条
C. 3条
D. 4条
4.小明用一根长为30厘米的铁丝围成一个直角三角形,使斜边长为13厘米,则该三角形的面积等于( )21·世纪*教育网
A. 15厘米2
B. 30厘米2
C. 45厘米2
D. 60厘米2
5.如图,在矩形ABCD中,AE,AF三等分∠BAD,若BE=2,CF=1,则最接近矩形面积的是( )www-2-1-cnjy-com
A. 13
B. 14
C. 15
D. 162
二、解答——知识提高运用
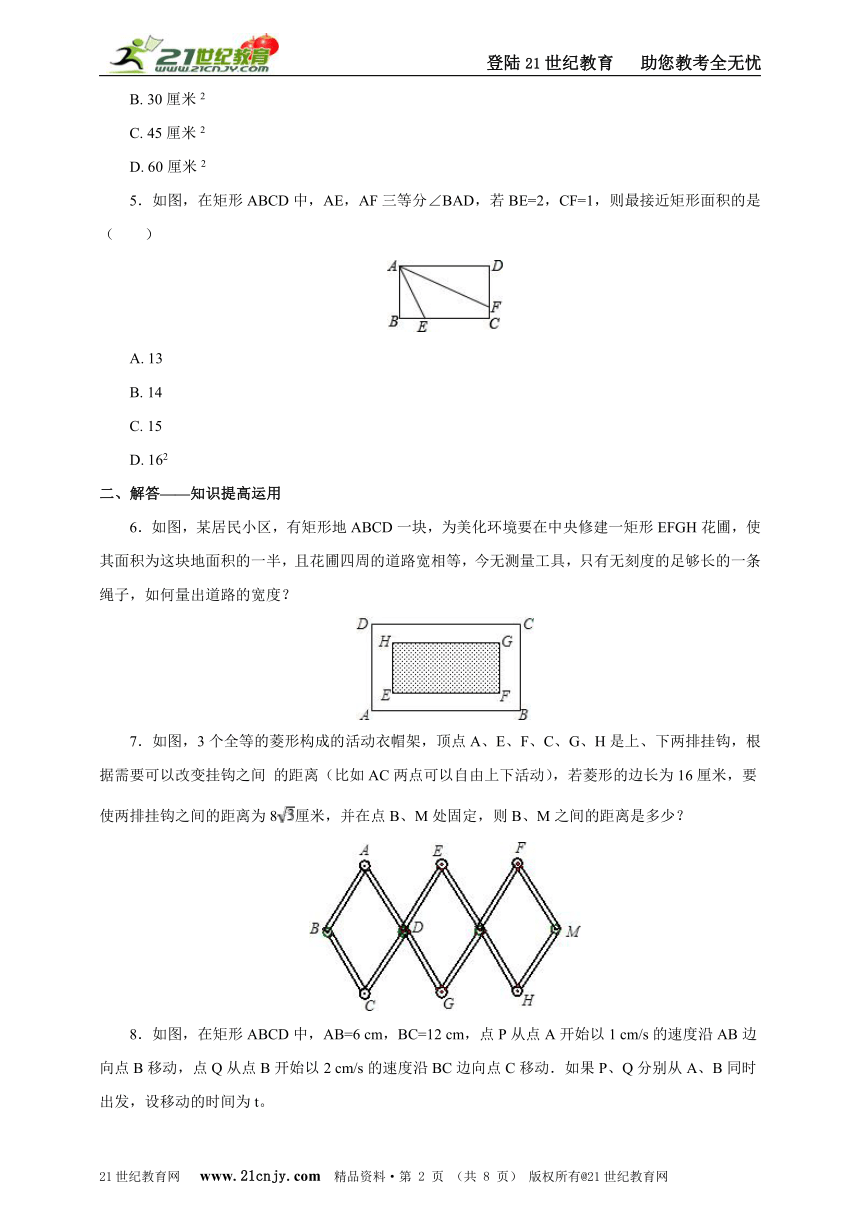
6.如图,某居民小区,有矩形地ABCD一块 ( http: / / www.21cnjy.com ),为美化环境要在中央修建一矩形EFGH花圃,使其面积为这块地面积的一半,且花圃四周的道路宽相等,今无测量工具,只有无刻度的足够长的一条绳子,如何量出道路的宽度?【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com / )
7.如图,3个全等的菱形构 ( http: / / www.21cnjy.com )成的活动衣帽架,顶点A、E、F、C、G、H是上、下两排挂钩,根据需要可以改变挂钩之间 的距离(比如AC两点可以自由上下活动),若菱形的边长为16厘米,要使两排挂钩之间的距离为8厘米,并在点B、M处固定,则B、M之间的距离是多少?
( http: / / www.21cnjy.com / )
8.如图,在矩形ABCD中,AB=6 ( http: / / www.21cnjy.com )cm,BC=12 cm,点P从点A开始以1 cm/s的速度沿AB边向点B移动,点Q从点B开始以2 cm/s的速度沿BC边向点C移动.如果P、Q分别从A、B同时出发,设移动的时间为t。21cnjy.com
( http: / / www.21cnjy.com / )
求:(1)当t为多少时,△PBQ的面积等于8 cm2?
(2)当t为多少时,△PQD是以PD为斜边的直角三角形?
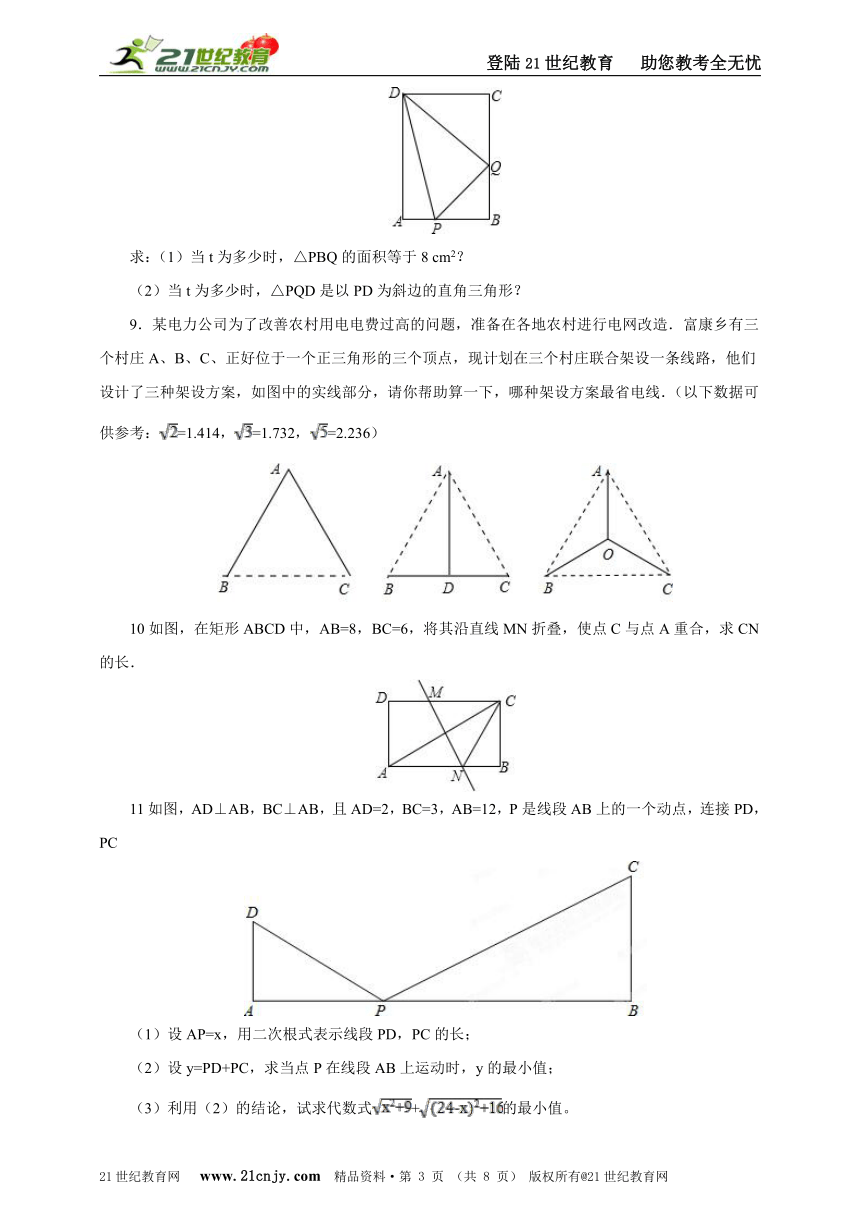
9.某电力公司为了改善农村用电电费 ( http: / / www.21cnjy.com )过高的问题,准备在各地农村进行电网改造.富康乡有三个村庄A、B、C、正好位于一个正三角形的三个顶点,现计划在三个村庄联合架设一条线路,他们设计了三种架设方案,如图中的实线部分,请你帮助算一下,哪种架设方案最省电线.(以下数据可供参考:=1.414,=1.732,=2.236)2-1-c-n-j-y
( http: / / www.21cnjy.com / )
10如图,在矩形ABCD中,AB=8,BC=6,将其沿直线MN折叠,使点C与点A重合,求CN的长.
( http: / / www.21cnjy.com / )
11如图,AD⊥AB,BC⊥AB,且AD=2,BC=3,AB=12,P是线段AB上的一个动点,连接PD,PC【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com / )
(1)设AP=x,用二次根式表示线段PD,PC的长;
(2)设y=PD+PC,求当点P在线段AB上运动时,y的最小值;
(3)利用(2)的结论,试求代数式+的最小值。
参考答案
一、选择——基础知识运用
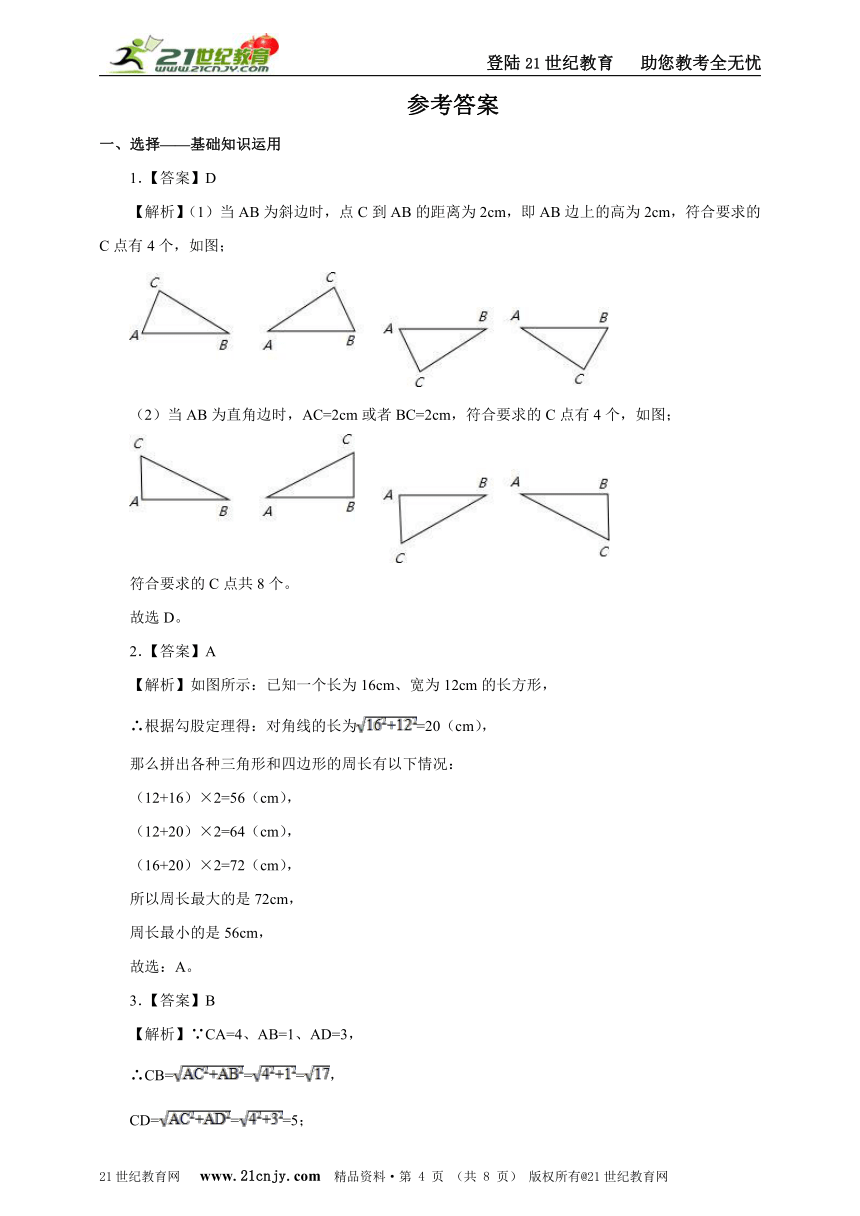
1.【答案】D
【解析】(1)当AB为斜边时,点C到AB的距离为2cm,即AB边上的高为2cm,符合要求的C点有4个,如图;www.21-cn-jy.com
( http: / / www.21cnjy.com / )
(2)当AB为直角边时,AC=2cm或者BC=2cm,符合要求的C点有4个,如图;
( http: / / www.21cnjy.com / )
符合要求的C点共8个。
故选D。
2.【答案】A
【解析】如图所示:已知一个长为16cm、宽为12cm的长方形,
∴根据勾股定理得:对角线的长为=20(cm),
那么拼出各种三角形和四边形的周长有以下情况:
(12+16)×2=56(cm),
(12+20)×2=64(cm),
(16+20)×2=72(cm),
所以周长最大的是72cm,
周长最小的是56cm,
故选:A。
3.【答案】B
【解析】∵CA=4、AB=1、AD=3,
∴CB===,
CD===5;
CE==2;
CF==,
∴长度为有理数的一共有2条,
故选B。
4.【答案】B
【解析】设一直角边为x,
x2+(30-13-x)2=132,
解得x=12或x=5,
当x=12时 另一边为30-13-12=5,
当x=5时 另一边为30-13-5=12,
所以面积为×12×5=30。
故选B。
5.【答案】C
【解析】矩形ABCD,∠B=∠D=∠BAD=90°,AB=CD
∵AE,AF三等分∠BAD,
∴∠BAE=∠EAF=∠DAF=30°,
∵BE=2,CF=1,
∴AE=4,
由勾股定理得:AB==2,
∴CD=2,
即:DF=2-1,
∴AF=2DF=4-2,
由勾股定理得:AD=6-,
∴矩形的面积是:AB×AD=(6-)×2=12-6≈14.784.
故选C。
二、解答——知识提高运用
6.【答案】设道路的宽为x,AB=a,AD=b,
则(a-2x)(b-2x)=ab,
x=,
∵2x=>>b(不合题意,舍去)
故x= =.
具体做法是:用绳量出AB+AD,再减去BD之长,将余下的AB+AD-BD对折两次,即得道路的宽x=。21*cnjy*com
7.【答案】连接AC,BD交于点O,
( http: / / www.21cnjy.com / )
∵四边形ABCD是菱形,
∴AO=AC=4
∴BO= ==4,
∴BD=8,
BM=24。
8.【答案】(1)AP=t,BP=6-t,BQ=2t,
△PBQ的面积等于8cm2
则(6-t)×2t=8
整理得t2-6t+8=0,解得t1=2,t2=4
即当t为2秒或4秒时,△PBQ的面积等于8cm2;
(2)易得PD2=t2+122,PQ2=(6-t)2+(2t)2,QD2=(12-2t)2+62,
∵△PQD是以PD为斜边的直角三角形
∴PD2=PQ2+QD2,即t2+122=(6-t)2+(2t)2+(12-2t)2+62,
整理得2t2-15t+18=0,解之得t1=6,t2=,
即当t为秒或6秒时,△PQD是以PD为斜边的直角三角形。
9.【答案】∵AB=BC=AC,
∴△ABC是等边三角形,
( http: / / www.21cnjy.com / )
设边长为2a,
则图(1)中电线长度为:l1=2a×2=4a;
图(2)中,电线的长度为:l2=2a+2a sin60°=2a+2a×=2a+a≈3.73a;
图(3)中,电线的长度为:l3=3× =3× =2a≈3.46a,【出处:21教育名师】
故l1>l2>l3。
故第3种方案最省电线。
10.【答案】设CN=x,则AN=CN=x,
∵AB=8,
∴BN=8-x,
∵四边形ABCD为矩形,
∴∠B=90°,
∴在Rt△CBN中,CN2=NB2+BC2,
又∵BC=6,
∴x2=(8-x)2+62
解得,x=6.25
答:CN的长为6.25。
11.【答案】(1)在直角△ADP中,∵∠A=90°,AD=2,AP=x,
∴PD==;
在直角△BCP中,∵∠B=90°,AD=3,PB=AB-AP=12-x,
∴PC==;
(2)如右图.作D点关于AB的对称点D′,连接CD′,交AB于P,则PD′=PD,CD′=PD′+PC=PD+PC,即为y的最小值。21教育网
( http: / / www.21cnjy.com / )
过D′作AB的平行线,交CB的延长线于E.
在△CED′中,∠E=90°,D′E=AB=12,CE=CB+BE=CB+AD=3+2=5,
由勾股定理,得CD′==13,
故y的最小值为13;
(3)如图.构造图形,AB=24,AD⊥AB,AD=3,BC=4,PA=x,PB=24-x,
PD=,PC=,
由对称性可知,PC+PD的最小值为PC+PD′=CD′==25.
故代数式的最小值为25。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 7 页 (共 8 页) 版权所有@21世纪教育网
《勾股定理》练习
一、选择——基础知识运用
1.同一平面内有A、B、C三点,A、B两点相距5cm,点C到直线AB的距离为2cm,且△ABC为直角三角形,则满足上述条件的点C有( )21·cn·jy·com
A. 2个
B. 4个
C. 6个
D. 8个
2.如图,用硬纸片剪一个长为16cm、宽 ( http: / / www.21cnjy.com )为12cm的长方形,再沿对角线把它分成两个三角形,用这两个三角形可拼出各种三角形和四边形来,其中周长最大的是( )cm,周长最小的是( )cm.21世纪教育网版权所有
( http: / / www.21cnjy.com / )
A. 72,56
B. 70,56
C. 70,54
D. 74,54
3.如图,是由16个边长为1的小正方形拼成 ( http: / / www.21cnjy.com )的,连接这些小正方形的若干个顶点,得到五条线段CA、CB、CD、CE、CF,其中长度是有理数的有( )2·1·c·n·j·y
( http: / / www.21cnjy.com / )
A. l条
B. 2条
C. 3条
D. 4条
4.小明用一根长为30厘米的铁丝围成一个直角三角形,使斜边长为13厘米,则该三角形的面积等于( )21·世纪*教育网
A. 15厘米2
B. 30厘米2
C. 45厘米2
D. 60厘米2
5.如图,在矩形ABCD中,AE,AF三等分∠BAD,若BE=2,CF=1,则最接近矩形面积的是( )www-2-1-cnjy-com
A. 13
B. 14
C. 15
D. 162
二、解答——知识提高运用
6.如图,某居民小区,有矩形地ABCD一块 ( http: / / www.21cnjy.com ),为美化环境要在中央修建一矩形EFGH花圃,使其面积为这块地面积的一半,且花圃四周的道路宽相等,今无测量工具,只有无刻度的足够长的一条绳子,如何量出道路的宽度?【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com / )
7.如图,3个全等的菱形构 ( http: / / www.21cnjy.com )成的活动衣帽架,顶点A、E、F、C、G、H是上、下两排挂钩,根据需要可以改变挂钩之间 的距离(比如AC两点可以自由上下活动),若菱形的边长为16厘米,要使两排挂钩之间的距离为8厘米,并在点B、M处固定,则B、M之间的距离是多少?
( http: / / www.21cnjy.com / )
8.如图,在矩形ABCD中,AB=6 ( http: / / www.21cnjy.com )cm,BC=12 cm,点P从点A开始以1 cm/s的速度沿AB边向点B移动,点Q从点B开始以2 cm/s的速度沿BC边向点C移动.如果P、Q分别从A、B同时出发,设移动的时间为t。21cnjy.com
( http: / / www.21cnjy.com / )
求:(1)当t为多少时,△PBQ的面积等于8 cm2?
(2)当t为多少时,△PQD是以PD为斜边的直角三角形?
9.某电力公司为了改善农村用电电费 ( http: / / www.21cnjy.com )过高的问题,准备在各地农村进行电网改造.富康乡有三个村庄A、B、C、正好位于一个正三角形的三个顶点,现计划在三个村庄联合架设一条线路,他们设计了三种架设方案,如图中的实线部分,请你帮助算一下,哪种架设方案最省电线.(以下数据可供参考:=1.414,=1.732,=2.236)2-1-c-n-j-y
( http: / / www.21cnjy.com / )
10如图,在矩形ABCD中,AB=8,BC=6,将其沿直线MN折叠,使点C与点A重合,求CN的长.
( http: / / www.21cnjy.com / )
11如图,AD⊥AB,BC⊥AB,且AD=2,BC=3,AB=12,P是线段AB上的一个动点,连接PD,PC【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com / )
(1)设AP=x,用二次根式表示线段PD,PC的长;
(2)设y=PD+PC,求当点P在线段AB上运动时,y的最小值;
(3)利用(2)的结论,试求代数式+的最小值。
参考答案
一、选择——基础知识运用
1.【答案】D
【解析】(1)当AB为斜边时,点C到AB的距离为2cm,即AB边上的高为2cm,符合要求的C点有4个,如图;www.21-cn-jy.com
( http: / / www.21cnjy.com / )
(2)当AB为直角边时,AC=2cm或者BC=2cm,符合要求的C点有4个,如图;
( http: / / www.21cnjy.com / )
符合要求的C点共8个。
故选D。
2.【答案】A
【解析】如图所示:已知一个长为16cm、宽为12cm的长方形,
∴根据勾股定理得:对角线的长为=20(cm),
那么拼出各种三角形和四边形的周长有以下情况:
(12+16)×2=56(cm),
(12+20)×2=64(cm),
(16+20)×2=72(cm),
所以周长最大的是72cm,
周长最小的是56cm,
故选:A。
3.【答案】B
【解析】∵CA=4、AB=1、AD=3,
∴CB===,
CD===5;
CE==2;
CF==,
∴长度为有理数的一共有2条,
故选B。
4.【答案】B
【解析】设一直角边为x,
x2+(30-13-x)2=132,
解得x=12或x=5,
当x=12时 另一边为30-13-12=5,
当x=5时 另一边为30-13-5=12,
所以面积为×12×5=30。
故选B。
5.【答案】C
【解析】矩形ABCD,∠B=∠D=∠BAD=90°,AB=CD
∵AE,AF三等分∠BAD,
∴∠BAE=∠EAF=∠DAF=30°,
∵BE=2,CF=1,
∴AE=4,
由勾股定理得:AB==2,
∴CD=2,
即:DF=2-1,
∴AF=2DF=4-2,
由勾股定理得:AD=6-,
∴矩形的面积是:AB×AD=(6-)×2=12-6≈14.784.
故选C。
二、解答——知识提高运用
6.【答案】设道路的宽为x,AB=a,AD=b,
则(a-2x)(b-2x)=ab,
x=,
∵2x=>>b(不合题意,舍去)
故x= =.
具体做法是:用绳量出AB+AD,再减去BD之长,将余下的AB+AD-BD对折两次,即得道路的宽x=。21*cnjy*com
7.【答案】连接AC,BD交于点O,
( http: / / www.21cnjy.com / )
∵四边形ABCD是菱形,
∴AO=AC=4
∴BO= ==4,
∴BD=8,
BM=24。
8.【答案】(1)AP=t,BP=6-t,BQ=2t,
△PBQ的面积等于8cm2
则(6-t)×2t=8
整理得t2-6t+8=0,解得t1=2,t2=4
即当t为2秒或4秒时,△PBQ的面积等于8cm2;
(2)易得PD2=t2+122,PQ2=(6-t)2+(2t)2,QD2=(12-2t)2+62,
∵△PQD是以PD为斜边的直角三角形
∴PD2=PQ2+QD2,即t2+122=(6-t)2+(2t)2+(12-2t)2+62,
整理得2t2-15t+18=0,解之得t1=6,t2=,
即当t为秒或6秒时,△PQD是以PD为斜边的直角三角形。
9.【答案】∵AB=BC=AC,
∴△ABC是等边三角形,
( http: / / www.21cnjy.com / )
设边长为2a,
则图(1)中电线长度为:l1=2a×2=4a;
图(2)中,电线的长度为:l2=2a+2a sin60°=2a+2a×=2a+a≈3.73a;
图(3)中,电线的长度为:l3=3× =3× =2a≈3.46a,【出处:21教育名师】
故l1>l2>l3。
故第3种方案最省电线。
10.【答案】设CN=x,则AN=CN=x,
∵AB=8,
∴BN=8-x,
∵四边形ABCD为矩形,
∴∠B=90°,
∴在Rt△CBN中,CN2=NB2+BC2,
又∵BC=6,
∴x2=(8-x)2+62
解得,x=6.25
答:CN的长为6.25。
11.【答案】(1)在直角△ADP中,∵∠A=90°,AD=2,AP=x,
∴PD==;
在直角△BCP中,∵∠B=90°,AD=3,PB=AB-AP=12-x,
∴PC==;
(2)如右图.作D点关于AB的对称点D′,连接CD′,交AB于P,则PD′=PD,CD′=PD′+PC=PD+PC,即为y的最小值。21教育网
( http: / / www.21cnjy.com / )
过D′作AB的平行线,交CB的延长线于E.
在△CED′中,∠E=90°,D′E=AB=12,CE=CB+BE=CB+AD=3+2=5,
由勾股定理,得CD′==13,
故y的最小值为13;
(3)如图.构造图形,AB=24,AD⊥AB,AD=3,BC=4,PA=x,PB=24-x,
PD=,PC=,
由对称性可知,PC+PD的最小值为PC+PD′=CD′==25.
故代数式的最小值为25。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 7 页 (共 8 页) 版权所有@21世纪教育网
