18.1.1平行四边形的性质练习
图片预览


文档简介
《平行四边形的性质》练习
一、选择——基础知识运用
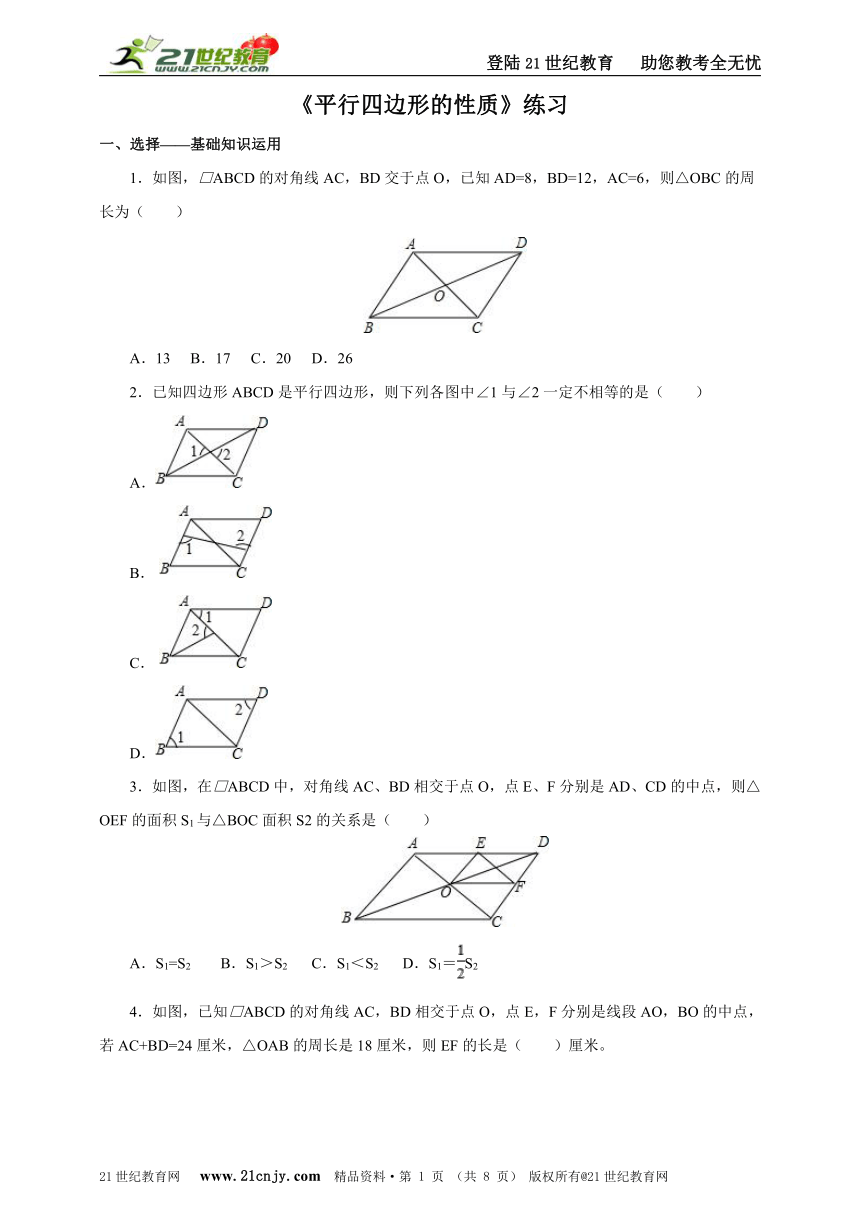
1.如图,□ABCD的对角线AC,BD交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为( )21世纪教育网版权所有
A.13 B.17 C.20 D.26
2.已知四边形ABCD是平行四边形,则下列各图中∠1与∠2一定不相等的是( )
A.
B.
C.
D.
3.如图,在□ABCD中,对角线AC、BD相交于点O,点E、F分别是AD、CD的中点,则△OEF的面积S1与△BOC面积S2的关系是( )21教育网
A.S1=S2 B.S1>S2 C.S1<S2 D.S1=S2
4.如图,已知□ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=24厘米,△OAB的周长是18厘米,则EF的长是( )厘米。
A.6 B.9 C.12 D.3
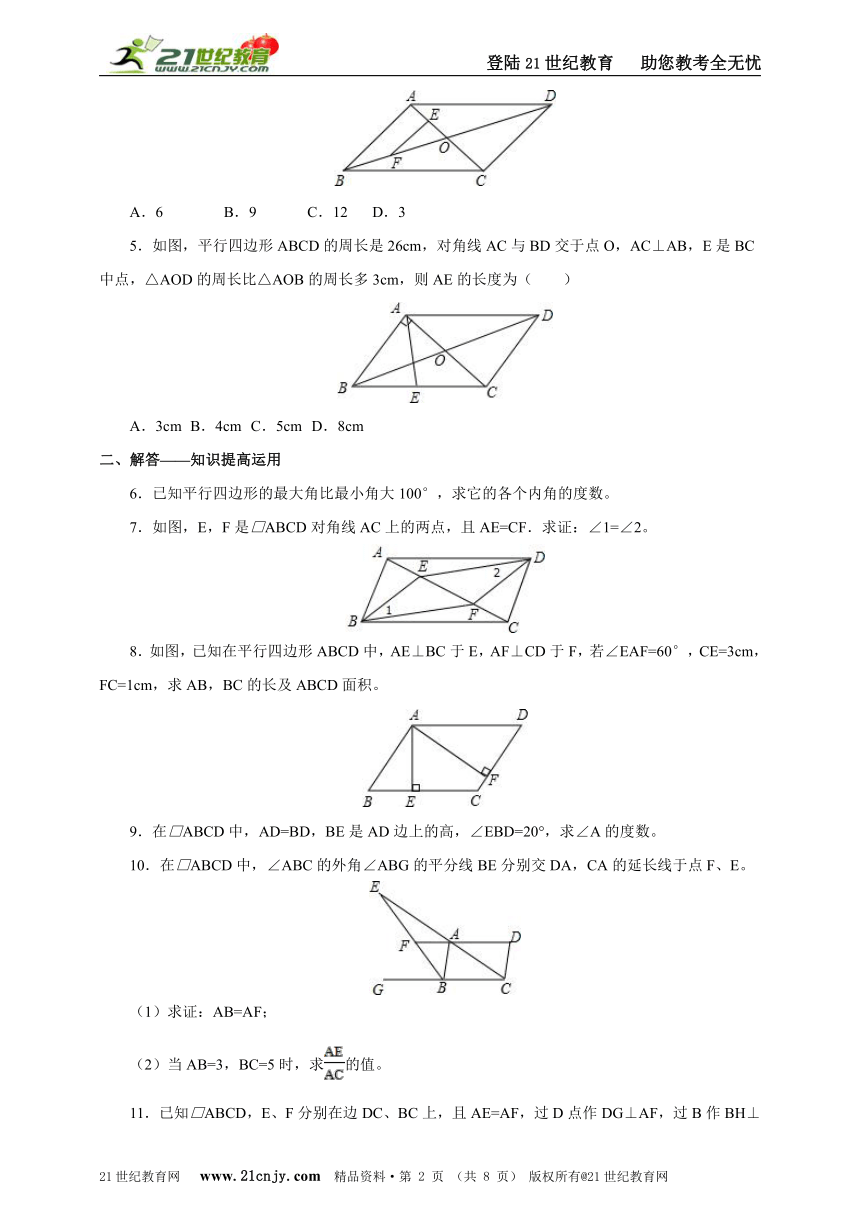
5.如图,平行四边形ABCD的周长是26cm,对角线AC与BD交于点O,AC⊥AB,E是BC中点,△AOD的周长比△AOB的周长多3cm,则AE的长度为( )21cnjy.com
A.3cm B.4cm C.5cm D.8cm
二、解答——知识提高运用
6.已知平行四边形的最大角比最小角大100°,求它的各个内角的度数。
7.如图,E,F是□ABCD对角线AC上的两点,且AE=CF.求证:∠1=∠2。
8.如图,已知在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,若∠EAF=60°,CE=3cm,FC=1cm,求AB,BC的长及ABCD面积。21·cn·jy·com
9.在□ABCD中,AD=BD,BE是AD边上的高,∠EBD=20°,求∠A的度数。
10.在□ABCD中,∠ABC的外角∠ABG的平分线BE分别交DA,CA的延长线于点F、E。
(1)求证:AB=AF;
(2)当AB=3,BC=5时,求的值。
11.已知□ABCD,E、F分别在边DC、BC上,且AE=AF,过D点作DG⊥AF,过B作BH⊥AE,求证:DG=BH。www.21-cn-jy.com
参考答案
一、选择——基础知识运用
1.【答案】B
【解析】∵四边形ABCD是平行四边形,
∴OA=OC=3,OB=OD=6,BC=AD=8,
∴△OBC的周长=OB+OC+AD=3+6+8=17。
故选:B。
2.【答案】C
【解析】
A正确;
∵∠1和∠2是对顶角,
∴∠1=∠2;
B、D正确;
∵四边形ABCD是平行四边形,
∴∠B=∠D,AB∥CD,
∴∠1=∠2;
C不正确;
故选:C。
3.【答案】D
【解析】∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,OB=OD,
∵点E、F分别是AD、CD的中点,
∴DE= AD= BC,OF= BC,OF∥BC,
∴DE∥OF,DE∥OF,
∴四边形OFDE是平行四边形,
∴△OEF的面积=△ODF的面积= △BCD的面积= △BOC的面积,
即S1=S2,
故选:D。
4.【答案】D
【解析】∵□ABCD的对角线AC,BD相交于点O,
∴OA=OC,OB=OD,
∵AC+BD=24厘米,
∴OB+0A=12厘米,
∵△OAB的周长是18厘米,
∴AB=18-12=6厘米,
∵点E,F分别是线段AO,BO的中点,
∴EF是△OAB的中位线,
∴EF=AB=3厘米,
故选:D。
5.【答案】B
【解析】∵□ABCD的周长为26cm,
∴AB+AD=13cm,OB=OD,
∵△AOD的周长比△AOB的周长多3cm,
∴(OA+OD+AD)-(OA+OB+AB)=AD-AB=3cm,
∴AB=5cm,AD=8cm。
∴BC=AD=8cm。
∵AC⊥AB,E是BC中点,
∴AE= BC=4cm;
故选:B。
二、解答——知识提高运用
6.【答案】
如图所示:
∵四边形ABCD是平行四边形,
∴∠A=∠C,∠B=∠D,
∴∠A+∠C+∠B+∠D=360°,
∴∠A+∠B=180°,
又∵∠A-∠B=100°,
∴∠A=140°,∠B=40°,
∴∠A=∠C=140°,∠B=∠D=40°。
7.【答案】连接BD,如图所示:
∵四边形ABCD是平行四边形,
∴OB=OD,OA=OC,
∵AE=CF,
∴OE=OF,
∴四边形BFDE是平行四边形,
∴∠1=∠2。
8.【答案】∵AE⊥BC,AF⊥CD,∠EAF=60°,
∴∠AEC=∠AFC=90°,
∴∠C=360°-∠AEC-∠EAF-∠AFC=120°,
∵四边形ABCD是平行四边形,
∴∠C+∠B=180°,
∴∠B=60°,
∴∠BAE=30°,
∴AB=2BE,
设BE=a,则AB=2a,
∵CE=3cm,FC=1cm,
∴DF=2a-1,
又∵∠AFD=90°,∠D=60°,
∴∠DAF=30°,
∴AD=2DF=4a-2,
∵AD=BC=a+3,
解得a=,
∴AB=2a= ,BC=a+3= +3= ,
∵∠AEB=90°,AB= ,BE=,
∴AE= ,
∴平行四边形ABCD的面积是:BC?AE= ×=,
即AB的长是cm,BC的长是cm,平行四边形ABCD的面积是cm2.。
9.【答案】根据平行四边形的性质和题意画出图形,分三种情况:①如图1所示
∵BE是AD边上的高,∠EBD=20°,
∴∠BDE=90°-20°=70°,
∵AD=BD,
∴∠A=∠ABD= (180°-70°)=55°;
②如图2所示:同①得:∠BDE=70°,
∵AD=BD,
∴∠A=∠ABD,
∴∠A=70°÷2=35°;
上所述:∠A的度数为55°或35°.
10.【答案】证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴DF∥BC,
∴∠AFB=∠FBG,
∵BF平分∠ABG,
∴∠ABF=∠FBG,
∴∠ABF=∠AFB,
∴AB=AF;
(2)解:∵FD∥CG,
∴△EFA∽△EBC,
∴===,
∴ =
11.【答案】连接BE、DF,如图所示:
∵△ADF的面积= AD?AD边上的高,△ABE的面积= AB?AB边上的高,
平行四边形ABCD的面积=AD?AD边上的高=AB?AB边上的高,
∴△ADF的面积= 平行四边形ABCD的面积=△ABE的面积,
∴AF?DG= AE?BH,
又∵AE=AF,
∴DG=BH。
一、选择——基础知识运用
1.如图,□ABCD的对角线AC,BD交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为( )21世纪教育网版权所有
A.13 B.17 C.20 D.26
2.已知四边形ABCD是平行四边形,则下列各图中∠1与∠2一定不相等的是( )
A.
B.
C.
D.
3.如图,在□ABCD中,对角线AC、BD相交于点O,点E、F分别是AD、CD的中点,则△OEF的面积S1与△BOC面积S2的关系是( )21教育网
A.S1=S2 B.S1>S2 C.S1<S2 D.S1=S2
4.如图,已知□ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=24厘米,△OAB的周长是18厘米,则EF的长是( )厘米。
A.6 B.9 C.12 D.3
5.如图,平行四边形ABCD的周长是26cm,对角线AC与BD交于点O,AC⊥AB,E是BC中点,△AOD的周长比△AOB的周长多3cm,则AE的长度为( )21cnjy.com
A.3cm B.4cm C.5cm D.8cm
二、解答——知识提高运用
6.已知平行四边形的最大角比最小角大100°,求它的各个内角的度数。
7.如图,E,F是□ABCD对角线AC上的两点,且AE=CF.求证:∠1=∠2。
8.如图,已知在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,若∠EAF=60°,CE=3cm,FC=1cm,求AB,BC的长及ABCD面积。21·cn·jy·com
9.在□ABCD中,AD=BD,BE是AD边上的高,∠EBD=20°,求∠A的度数。
10.在□ABCD中,∠ABC的外角∠ABG的平分线BE分别交DA,CA的延长线于点F、E。
(1)求证:AB=AF;
(2)当AB=3,BC=5时,求的值。
11.已知□ABCD,E、F分别在边DC、BC上,且AE=AF,过D点作DG⊥AF,过B作BH⊥AE,求证:DG=BH。www.21-cn-jy.com
参考答案
一、选择——基础知识运用
1.【答案】B
【解析】∵四边形ABCD是平行四边形,
∴OA=OC=3,OB=OD=6,BC=AD=8,
∴△OBC的周长=OB+OC+AD=3+6+8=17。
故选:B。
2.【答案】C
【解析】
A正确;
∵∠1和∠2是对顶角,
∴∠1=∠2;
B、D正确;
∵四边形ABCD是平行四边形,
∴∠B=∠D,AB∥CD,
∴∠1=∠2;
C不正确;
故选:C。
3.【答案】D
【解析】∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,OB=OD,
∵点E、F分别是AD、CD的中点,
∴DE= AD= BC,OF= BC,OF∥BC,
∴DE∥OF,DE∥OF,
∴四边形OFDE是平行四边形,
∴△OEF的面积=△ODF的面积= △BCD的面积= △BOC的面积,
即S1=S2,
故选:D。
4.【答案】D
【解析】∵□ABCD的对角线AC,BD相交于点O,
∴OA=OC,OB=OD,
∵AC+BD=24厘米,
∴OB+0A=12厘米,
∵△OAB的周长是18厘米,
∴AB=18-12=6厘米,
∵点E,F分别是线段AO,BO的中点,
∴EF是△OAB的中位线,
∴EF=AB=3厘米,
故选:D。
5.【答案】B
【解析】∵□ABCD的周长为26cm,
∴AB+AD=13cm,OB=OD,
∵△AOD的周长比△AOB的周长多3cm,
∴(OA+OD+AD)-(OA+OB+AB)=AD-AB=3cm,
∴AB=5cm,AD=8cm。
∴BC=AD=8cm。
∵AC⊥AB,E是BC中点,
∴AE= BC=4cm;
故选:B。
二、解答——知识提高运用
6.【答案】
如图所示:
∵四边形ABCD是平行四边形,
∴∠A=∠C,∠B=∠D,
∴∠A+∠C+∠B+∠D=360°,
∴∠A+∠B=180°,
又∵∠A-∠B=100°,
∴∠A=140°,∠B=40°,
∴∠A=∠C=140°,∠B=∠D=40°。
7.【答案】连接BD,如图所示:
∵四边形ABCD是平行四边形,
∴OB=OD,OA=OC,
∵AE=CF,
∴OE=OF,
∴四边形BFDE是平行四边形,
∴∠1=∠2。
8.【答案】∵AE⊥BC,AF⊥CD,∠EAF=60°,
∴∠AEC=∠AFC=90°,
∴∠C=360°-∠AEC-∠EAF-∠AFC=120°,
∵四边形ABCD是平行四边形,
∴∠C+∠B=180°,
∴∠B=60°,
∴∠BAE=30°,
∴AB=2BE,
设BE=a,则AB=2a,
∵CE=3cm,FC=1cm,
∴DF=2a-1,
又∵∠AFD=90°,∠D=60°,
∴∠DAF=30°,
∴AD=2DF=4a-2,
∵AD=BC=a+3,
解得a=,
∴AB=2a= ,BC=a+3= +3= ,
∵∠AEB=90°,AB= ,BE=,
∴AE= ,
∴平行四边形ABCD的面积是:BC?AE= ×=,
即AB的长是cm,BC的长是cm,平行四边形ABCD的面积是cm2.。
9.【答案】根据平行四边形的性质和题意画出图形,分三种情况:①如图1所示
∵BE是AD边上的高,∠EBD=20°,
∴∠BDE=90°-20°=70°,
∵AD=BD,
∴∠A=∠ABD= (180°-70°)=55°;
②如图2所示:同①得:∠BDE=70°,
∵AD=BD,
∴∠A=∠ABD,
∴∠A=70°÷2=35°;
上所述:∠A的度数为55°或35°.
10.【答案】证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴DF∥BC,
∴∠AFB=∠FBG,
∵BF平分∠ABG,
∴∠ABF=∠FBG,
∴∠ABF=∠AFB,
∴AB=AF;
(2)解:∵FD∥CG,
∴△EFA∽△EBC,
∴===,
∴ =
11.【答案】连接BE、DF,如图所示:
∵△ADF的面积= AD?AD边上的高,△ABE的面积= AB?AB边上的高,
平行四边形ABCD的面积=AD?AD边上的高=AB?AB边上的高,
∴△ADF的面积= 平行四边形ABCD的面积=△ABE的面积,
∴AF?DG= AE?BH,
又∵AE=AF,
∴DG=BH。
