18.2.5正方形练习
图片预览


文档简介
《正方形》练习
一、选择——基础知识运用
1.下列命题中,真命题是( )
A.对角线相等的四边形是矩形
B.对角线互相垂直的四边形是菱形
C.对角线互相平分的四边形是平行四边形
D.对角线互相垂直平分的四边形是正方形
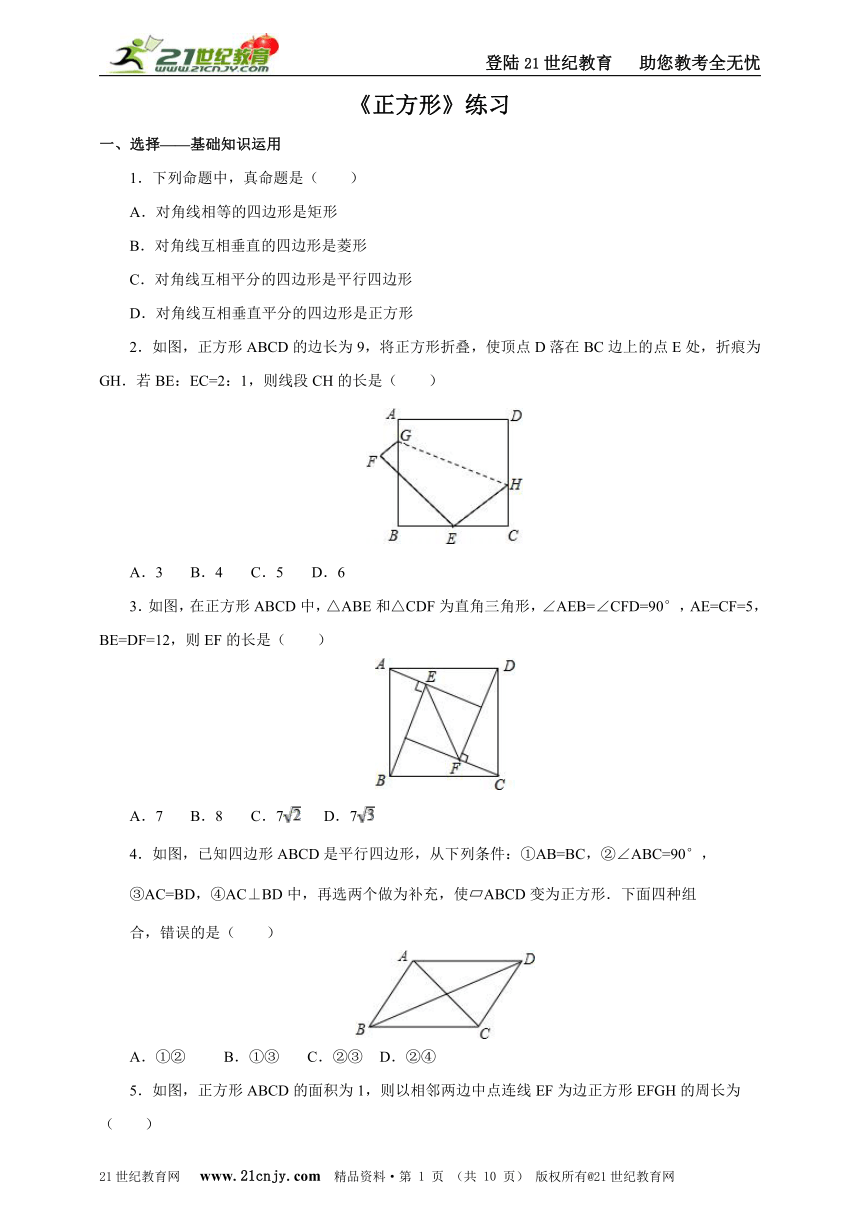
2.如图,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH.若BE:EC=2:1,则线段CH的长是( )21世纪教育网版权所有
A.3 B.4 C.5 D.6
3.如图,在正方形ABCD中,△ABE和△CDF为直角三角形,∠AEB=∠CFD=90°,AE=CF=5,BE=DF=12,则EF的长是( )21教育网
A.7 B.8 C.7 D.7
4.如图,已知四边形ABCD是平行四边形,从下列条件:①AB=BC,②∠ABC=90°,
③AC=BD,④AC⊥BD中,再选两个做为补充,使?ABCD变为正方形.下面四种组
合,错误的是( )
A.①② B.①③ C.②③ D.②④
5.如图,正方形ABCD的面积为1,则以相邻两边中点连线EF为边正方形EFGH的周长为( )
A. B.2C.+1 D.2+1
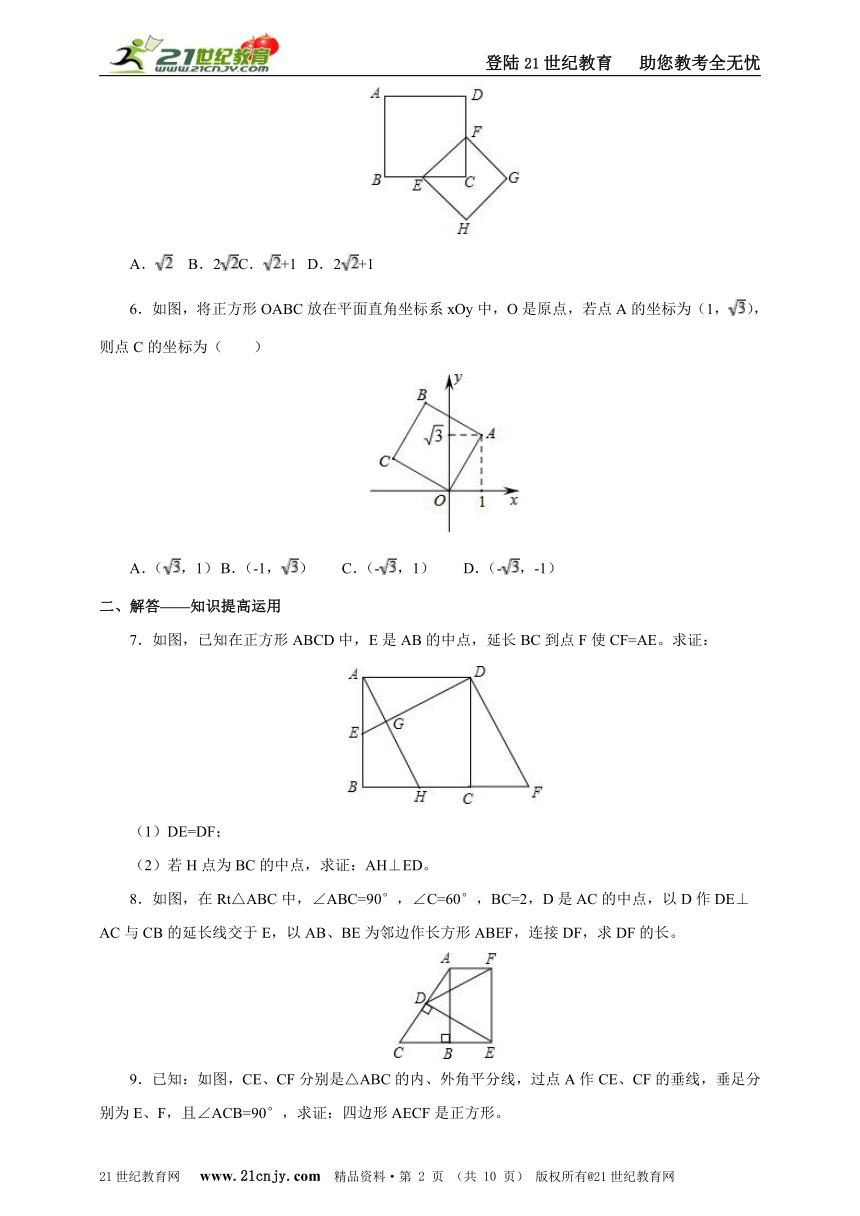
6.如图,将正方形OABC放在平面直角坐标系xOy中,O是原点,若点A的坐标为(1,),则点C的坐标为( )21cnjy.com
A.(,1) B.(-1,) C.(-,1) D.(-,-1)
二、解答——知识提高运用
7.如图,已知在正方形ABCD中,E是AB的中点,延长BC到点F使CF=AE。求证:
(1)DE=DF;
(2)若H点为BC的中点,求证:AH⊥ED。
8.如图,在Rt△ABC中,∠ABC=90°,∠C=60°,BC=2,D是AC的中点,以D作DE⊥AC与CB的延长线交于E,以AB、BE为邻边作长方形ABEF,连接DF,求DF的长。
9.已知:如图,CE、CF分别是△ABC的内、外角平分线,过点A作CE、CF的垂线,垂足分别为E、F,且∠ACB=90°,求证:四边形AECF是正方形。21·cn·jy·com
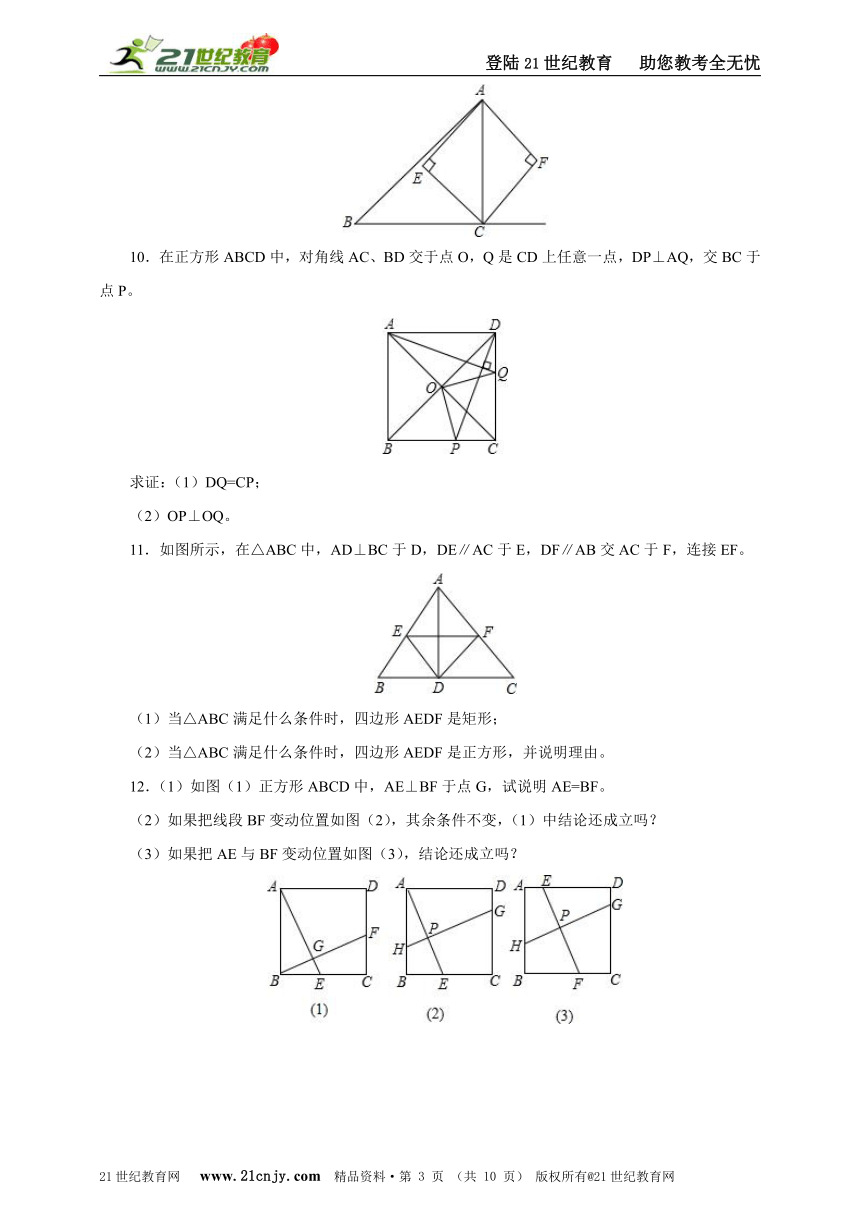
10.在正方形ABCD中,对角线AC、BD交于点O,Q是CD上任意一点,DP⊥AQ,交BC于点P。
求证:(1)DQ=CP;
(2)OP⊥OQ。
11.如图所示,在△ABC中,AD⊥BC于D,DE∥AC于E,DF∥AB交AC于F,连接EF。
(1)当△ABC满足什么条件时,四边形AEDF是矩形;
(2)当△ABC满足什么条件时,四边形AEDF是正方形,并说明理由。
12.(1)如图(1)正方形ABCD中,AE⊥BF于点G,试说明AE=BF。
(2)如果把线段BF变动位置如图(2),其余条件不变,(1)中结论还成立吗?
(3)如果把AE与BF变动位置如图(3),结论还成立吗?
参考答案
一、选择——基础知识运用
1.【答案】C
【解析】A、两条对角线相等且相互平分的四边形为矩形;故本选项错误;
B、对角线互相垂直的平行四边形是菱形;故本选项错误;
C、对角线互相平分的四边形是平行四边形;故本选项正确;
D、对角线互相垂直平分且相等的四边形是正方形;故本选项错误;
故选C。
2.【答案】B
【解析】设CH=x,则DH=EH=9-x,
∵BE:EC=2:1,BC=9,
∴CE= BC=3,
∴在Rt△ECH中,EH2=EC2+CH2,
即(9-x)2=32+x2,
解得:x=4,
即CH=4。
故选B。
3.【答案】C
【解析】∵四边形ABCD是正方形,
∴∠BAD=∠ABC=∠BCD=∠ADC=90°,AB=BC=CD=AD,
∴∠BAE+∠DAG=90°,
在△ABE和△CDF中,
AB=CD ;AE=CF ;BE=DF ,
∴△ABE≌△CDF(SSS),
∴∠ABE=∠CDF,
∵∠AEB=∠CFD=90°,
∴∠ABE+∠BAE=90°,
∴∠ABE=∠DAG=∠CDF,
同理:∠ABE=∠DAG=∠CDF=∠BCH,
∴∠DAG+∠ADG=∠CDF+∠ADG=90°,
即∠DGA=90°,
同理:∠CHB=90°,
在△ABE和△ADG中,
∠ABE=∠DAG ;∠AEB=∠DGA=90° ;AB=DA ,
∴△ABE≌△ADG(AAS),
∴AE=DG,BE=AG,
同理:AE=DG=CF=BH=5,BE=AG=DF=CH=12,
∴EG=GF=FH=EF=12-5=7,
∵∠GEH=180°-90°=90°,
∴四边形EGFH是正方形,
∴EF=EG=7;
故选:C。
4.【答案】C
【解析】A、由①得有一组邻边相等的平行四边形是菱形,由②得有一个角是直角的平行四边形是矩形,
所以平行四边形ABCD是正方形,正确,故本选项不符合题意;
B、由①得有一组邻边相等的平行四边形是菱形,由③得对角线相等的平行四边形是矩形,
所以平行四边形ABCD是正方形,正确,故本选项不符合题意;
C、由②得有一个角是直角的平行四边形是矩形,由③得对角线相等的平行四边形是矩形,
所以不能得出平行四边形ABCD是正方形,错误,故本选项符合题意;
D、由②得有一个角是直角的平行四边形是矩形,由④得对角线互相垂直的平行四边形是菱形,
所以平行四边形ABCD是正方形,正确,故本选项不符合题意;
故选:C。
5.【答案】B
【解析】∵正方形ABCD的面积为1,
∴BC=CD=1,∠BCD=90°,
∵E、F分别是BC、CD的中点,
∴CE= BC= ,CF= CD= ,
∴CE=CF,
∴△CEF是等腰直角三角形,
∴EF=CE=,
∴正方形EFGH的周长=4EF=4×=2;
故选:B。
6.【答案】C
【解析】作AD⊥轴于D,作CE⊥x轴于E,如图所示:
则∠ADO=∠OEC=90°,
∴∠1+∠2=90°,
∵点A的坐标为(1,),
∴OD=1,AD=,
∵四边形OABC是正方形,
∴∠AOC=90°,OC=AO,
∴∠1+∠3=90°,
∴∠3=∠2,
在△OCE和△AOD中,
∠OEC=∠ADO ;∠3=∠2 ;OC=AO ,
∴△OCE≌△AOD(AAS),
∴OE=AD=,CE=OD=1,
∴点C的坐标为(-,1);
故选:C。
二、解答——知识提高运用
7.【答案】(1)在△AED和△DFC中,
CF=AE;∠DCF=∠DAE;AD=CD,
∴△ADE≌△CDF,(SAS)
∴DE=DF;
(2)在Rt△ADE和Rt△BAH中,
DA=AB;∠DAE=∠ABH;AE=BH,
∴△DAE≌△ABH(SAS),
∴∠EAG=∠ADG,
∵∠ADG+∠AEG=90°,
∴∠EAG+∠AEG=90°,
∴∠AGE=180°-∠EAG-∠AEG=90°,
即AH⊥DE。
8.【答案】∵△ABC为直角三角形,∠C=60°,
∴∠BAC=30°,
∴BC= AC,
∵D为AC的中点,
∴BC=DC,
∴在△DEC≌△BAC中,
BC=DC;∠C=∠C;∠ABC=∠EDC,
∴△DEC≌△BAC,
即AB=DE,∠DEB=30°,
∴∠FED=60°,
∵EF=AB,∴EF=DE,
∴△DEF为等边三角形,
即DF=AB,
在直角三角形ABC中,BC=2,则AC=4
AB=2。
答:DF的长为2。
9.【答案】∵CE、CF分别是△ABC的内外角平分线,
∴∠ACE+∠ACF= ×180°=90°,
∵AE⊥CE,AF⊥CF,
∴∠AEC=∠AFC=90°,
∴四边形AECF是矩形,
∵∠ACE= ∠ACB=45°,
∴∠EAC=45°=∠ACE,
∴AE=CE,
∴四边形AECF是正方形.°。
10.【答案】(1)∵AD=CD,∠DCP=∠ADQ,
∠DQM+∠PDC=90°,∠DQM+∠DAQ=90°,
∴∠PDC=∠QAD,
在△DCP和△ADQ中,
∠PDC=∠DAQ;CD=AD;∠PCD=∠QDA,
∴△DCP≌△ADQ,
∴DQ=CP。
(2)证:
在△OPC和△OQD中,
∵CP=DQ;∠OCP=∠ODQ;DO=CO,
∴△OPC≌△OQD,
∴∠POC=∠QOD,
∵∠QOD+∠QOC=90°
∴∠POC+∠QOC=∠POQ=90°,即OQ⊥OP。
11.【答案】(1)当△ABC满足∠BAC=90°时,四边形AEDF是矩形;理由如下:
∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,
又∵∠BAC=90°,
∴四边形AEDF是矩形;
故答案为:∠BAC=90°;
(2)当△ABC满足∠BAC=90°,且AB=AC时,四边形AEDF是正方形;理由如下:
由(1)得:当∠BAC=90°时,四边形AEDF是矩形,
又∵AB=AC,
∴∠B=∠C=45°,
∵AD⊥BC,
∴△ABD和△ACD是等腰直角三角形,
∵DE∥AC,
∴DE⊥AB,
∴AE=BE,
∴DE= AB,
同理:DF=AC,
∴DE=DF,
∴四边形AEDF是正方形;
故答案为:∠BAC=90°,且AB=AC。
12.【答案】
(1)AE=BF,
理由是:∵正方形ABCD,AE⊥BF,
∴AB=BC,∠C=∠ABE=∠AGB=90°,
∴∠BAE+∠ABG=90°,∠ABG+∠CBF=90°,
∴∠BAE=∠FBC,
在△ABE和△BCF中
∠ABE=∠C;AB=BC;∠BAE=∠CBF,
∴△ABE≌△BCF,
∴AE=BF。
(2)结论还成立,
理由是:过H作HM⊥CD于M,
∵正方形ABCD,AE⊥HG,
∴AB=BC=HM,∠B=∠APH=∠HMG=∠AHM=90°,
∴∠BAE+∠AHP=90°,∠GHM+∠AHP=90°,
∴∠BAE=∠GHM,
与(1)证法类似:证△ABE≌△HMG,
即AE=HG。
(3)结论还成立,
理由是:过E作EN⊥BC于N,
由EN∥AB∥CD,HM∥BC∥AD,EN=AB=BC=HM,
∵∠EPH=∠HOE=90°,∠EQP=∠HQN,
∴∠NEF=∠GHM,
在△ENF和△HMG中
∠ENF=∠HMG;EN=HM;∠NEF=∠MHG,
∴△ENF≌△HMG,
∴EF=HG。
一、选择——基础知识运用
1.下列命题中,真命题是( )
A.对角线相等的四边形是矩形
B.对角线互相垂直的四边形是菱形
C.对角线互相平分的四边形是平行四边形
D.对角线互相垂直平分的四边形是正方形
2.如图,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH.若BE:EC=2:1,则线段CH的长是( )21世纪教育网版权所有
A.3 B.4 C.5 D.6
3.如图,在正方形ABCD中,△ABE和△CDF为直角三角形,∠AEB=∠CFD=90°,AE=CF=5,BE=DF=12,则EF的长是( )21教育网
A.7 B.8 C.7 D.7
4.如图,已知四边形ABCD是平行四边形,从下列条件:①AB=BC,②∠ABC=90°,
③AC=BD,④AC⊥BD中,再选两个做为补充,使?ABCD变为正方形.下面四种组
合,错误的是( )
A.①② B.①③ C.②③ D.②④
5.如图,正方形ABCD的面积为1,则以相邻两边中点连线EF为边正方形EFGH的周长为( )
A. B.2C.+1 D.2+1
6.如图,将正方形OABC放在平面直角坐标系xOy中,O是原点,若点A的坐标为(1,),则点C的坐标为( )21cnjy.com
A.(,1) B.(-1,) C.(-,1) D.(-,-1)
二、解答——知识提高运用
7.如图,已知在正方形ABCD中,E是AB的中点,延长BC到点F使CF=AE。求证:
(1)DE=DF;
(2)若H点为BC的中点,求证:AH⊥ED。
8.如图,在Rt△ABC中,∠ABC=90°,∠C=60°,BC=2,D是AC的中点,以D作DE⊥AC与CB的延长线交于E,以AB、BE为邻边作长方形ABEF,连接DF,求DF的长。
9.已知:如图,CE、CF分别是△ABC的内、外角平分线,过点A作CE、CF的垂线,垂足分别为E、F,且∠ACB=90°,求证:四边形AECF是正方形。21·cn·jy·com
10.在正方形ABCD中,对角线AC、BD交于点O,Q是CD上任意一点,DP⊥AQ,交BC于点P。
求证:(1)DQ=CP;
(2)OP⊥OQ。
11.如图所示,在△ABC中,AD⊥BC于D,DE∥AC于E,DF∥AB交AC于F,连接EF。
(1)当△ABC满足什么条件时,四边形AEDF是矩形;
(2)当△ABC满足什么条件时,四边形AEDF是正方形,并说明理由。
12.(1)如图(1)正方形ABCD中,AE⊥BF于点G,试说明AE=BF。
(2)如果把线段BF变动位置如图(2),其余条件不变,(1)中结论还成立吗?
(3)如果把AE与BF变动位置如图(3),结论还成立吗?
参考答案
一、选择——基础知识运用
1.【答案】C
【解析】A、两条对角线相等且相互平分的四边形为矩形;故本选项错误;
B、对角线互相垂直的平行四边形是菱形;故本选项错误;
C、对角线互相平分的四边形是平行四边形;故本选项正确;
D、对角线互相垂直平分且相等的四边形是正方形;故本选项错误;
故选C。
2.【答案】B
【解析】设CH=x,则DH=EH=9-x,
∵BE:EC=2:1,BC=9,
∴CE= BC=3,
∴在Rt△ECH中,EH2=EC2+CH2,
即(9-x)2=32+x2,
解得:x=4,
即CH=4。
故选B。
3.【答案】C
【解析】∵四边形ABCD是正方形,
∴∠BAD=∠ABC=∠BCD=∠ADC=90°,AB=BC=CD=AD,
∴∠BAE+∠DAG=90°,
在△ABE和△CDF中,
AB=CD ;AE=CF ;BE=DF ,
∴△ABE≌△CDF(SSS),
∴∠ABE=∠CDF,
∵∠AEB=∠CFD=90°,
∴∠ABE+∠BAE=90°,
∴∠ABE=∠DAG=∠CDF,
同理:∠ABE=∠DAG=∠CDF=∠BCH,
∴∠DAG+∠ADG=∠CDF+∠ADG=90°,
即∠DGA=90°,
同理:∠CHB=90°,
在△ABE和△ADG中,
∠ABE=∠DAG ;∠AEB=∠DGA=90° ;AB=DA ,
∴△ABE≌△ADG(AAS),
∴AE=DG,BE=AG,
同理:AE=DG=CF=BH=5,BE=AG=DF=CH=12,
∴EG=GF=FH=EF=12-5=7,
∵∠GEH=180°-90°=90°,
∴四边形EGFH是正方形,
∴EF=EG=7;
故选:C。
4.【答案】C
【解析】A、由①得有一组邻边相等的平行四边形是菱形,由②得有一个角是直角的平行四边形是矩形,
所以平行四边形ABCD是正方形,正确,故本选项不符合题意;
B、由①得有一组邻边相等的平行四边形是菱形,由③得对角线相等的平行四边形是矩形,
所以平行四边形ABCD是正方形,正确,故本选项不符合题意;
C、由②得有一个角是直角的平行四边形是矩形,由③得对角线相等的平行四边形是矩形,
所以不能得出平行四边形ABCD是正方形,错误,故本选项符合题意;
D、由②得有一个角是直角的平行四边形是矩形,由④得对角线互相垂直的平行四边形是菱形,
所以平行四边形ABCD是正方形,正确,故本选项不符合题意;
故选:C。
5.【答案】B
【解析】∵正方形ABCD的面积为1,
∴BC=CD=1,∠BCD=90°,
∵E、F分别是BC、CD的中点,
∴CE= BC= ,CF= CD= ,
∴CE=CF,
∴△CEF是等腰直角三角形,
∴EF=CE=,
∴正方形EFGH的周长=4EF=4×=2;
故选:B。
6.【答案】C
【解析】作AD⊥轴于D,作CE⊥x轴于E,如图所示:
则∠ADO=∠OEC=90°,
∴∠1+∠2=90°,
∵点A的坐标为(1,),
∴OD=1,AD=,
∵四边形OABC是正方形,
∴∠AOC=90°,OC=AO,
∴∠1+∠3=90°,
∴∠3=∠2,
在△OCE和△AOD中,
∠OEC=∠ADO ;∠3=∠2 ;OC=AO ,
∴△OCE≌△AOD(AAS),
∴OE=AD=,CE=OD=1,
∴点C的坐标为(-,1);
故选:C。
二、解答——知识提高运用
7.【答案】(1)在△AED和△DFC中,
CF=AE;∠DCF=∠DAE;AD=CD,
∴△ADE≌△CDF,(SAS)
∴DE=DF;
(2)在Rt△ADE和Rt△BAH中,
DA=AB;∠DAE=∠ABH;AE=BH,
∴△DAE≌△ABH(SAS),
∴∠EAG=∠ADG,
∵∠ADG+∠AEG=90°,
∴∠EAG+∠AEG=90°,
∴∠AGE=180°-∠EAG-∠AEG=90°,
即AH⊥DE。
8.【答案】∵△ABC为直角三角形,∠C=60°,
∴∠BAC=30°,
∴BC= AC,
∵D为AC的中点,
∴BC=DC,
∴在△DEC≌△BAC中,
BC=DC;∠C=∠C;∠ABC=∠EDC,
∴△DEC≌△BAC,
即AB=DE,∠DEB=30°,
∴∠FED=60°,
∵EF=AB,∴EF=DE,
∴△DEF为等边三角形,
即DF=AB,
在直角三角形ABC中,BC=2,则AC=4
AB=2。
答:DF的长为2。
9.【答案】∵CE、CF分别是△ABC的内外角平分线,
∴∠ACE+∠ACF= ×180°=90°,
∵AE⊥CE,AF⊥CF,
∴∠AEC=∠AFC=90°,
∴四边形AECF是矩形,
∵∠ACE= ∠ACB=45°,
∴∠EAC=45°=∠ACE,
∴AE=CE,
∴四边形AECF是正方形.°。
10.【答案】(1)∵AD=CD,∠DCP=∠ADQ,
∠DQM+∠PDC=90°,∠DQM+∠DAQ=90°,
∴∠PDC=∠QAD,
在△DCP和△ADQ中,
∠PDC=∠DAQ;CD=AD;∠PCD=∠QDA,
∴△DCP≌△ADQ,
∴DQ=CP。
(2)证:
在△OPC和△OQD中,
∵CP=DQ;∠OCP=∠ODQ;DO=CO,
∴△OPC≌△OQD,
∴∠POC=∠QOD,
∵∠QOD+∠QOC=90°
∴∠POC+∠QOC=∠POQ=90°,即OQ⊥OP。
11.【答案】(1)当△ABC满足∠BAC=90°时,四边形AEDF是矩形;理由如下:
∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,
又∵∠BAC=90°,
∴四边形AEDF是矩形;
故答案为:∠BAC=90°;
(2)当△ABC满足∠BAC=90°,且AB=AC时,四边形AEDF是正方形;理由如下:
由(1)得:当∠BAC=90°时,四边形AEDF是矩形,
又∵AB=AC,
∴∠B=∠C=45°,
∵AD⊥BC,
∴△ABD和△ACD是等腰直角三角形,
∵DE∥AC,
∴DE⊥AB,
∴AE=BE,
∴DE= AB,
同理:DF=AC,
∴DE=DF,
∴四边形AEDF是正方形;
故答案为:∠BAC=90°,且AB=AC。
12.【答案】
(1)AE=BF,
理由是:∵正方形ABCD,AE⊥BF,
∴AB=BC,∠C=∠ABE=∠AGB=90°,
∴∠BAE+∠ABG=90°,∠ABG+∠CBF=90°,
∴∠BAE=∠FBC,
在△ABE和△BCF中
∠ABE=∠C;AB=BC;∠BAE=∠CBF,
∴△ABE≌△BCF,
∴AE=BF。
(2)结论还成立,
理由是:过H作HM⊥CD于M,
∵正方形ABCD,AE⊥HG,
∴AB=BC=HM,∠B=∠APH=∠HMG=∠AHM=90°,
∴∠BAE+∠AHP=90°,∠GHM+∠AHP=90°,
∴∠BAE=∠GHM,
与(1)证法类似:证△ABE≌△HMG,
即AE=HG。
(3)结论还成立,
理由是:过E作EN⊥BC于N,
由EN∥AB∥CD,HM∥BC∥AD,EN=AB=BC=HM,
∵∠EPH=∠HOE=90°,∠EQP=∠HQN,
∴∠NEF=∠GHM,
在△ENF和△HMG中
∠ENF=∠HMG;EN=HM;∠NEF=∠MHG,
∴△ENF≌△HMG,
∴EF=HG。
