第5周 3.1图形的平移-3.2图形的旋转同步测试
文档属性
| 名称 | 第5周 3.1图形的平移-3.2图形的旋转同步测试 |

|
|
| 格式 | zip | ||
| 文件大小 | 178.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-11 00:00:00 | ||
图片预览


文档简介
【新北师大版八年级数学(下)周周测】
第 5周测试卷
(测试范围:3.1图形的平移——3.2图形的旋转)
班级:___________ 姓名:___________ 得分:___________
一、选择题:(每小题3分共30分)
1. 观察下面图案,在A、B、C、D四幅图案中,能通过图案(1)的平移得到的是( )
2.如图,△ABC沿着由点B到点E的方向,平移到△DEF,已知BC=5.EC=3,那么平移的距离为( ).21教育网
A.2 B.3 C.5 D.7
3.下列运动属于平移的是( )
A.荡秋千
B.地球绕着太阳转
C.风筝在空中随风飘动
D.急刹车时,汽车在地面上的滑动
4.如图,在平面直角坐标系中,点A的坐标为(0,3),△OAB沿x轴向右平移后得到△O′A′B′,点A的对应点在直线y=x上一点,则点B与其对应点B′间的距离为( )
A. B.3 C.4 D.5
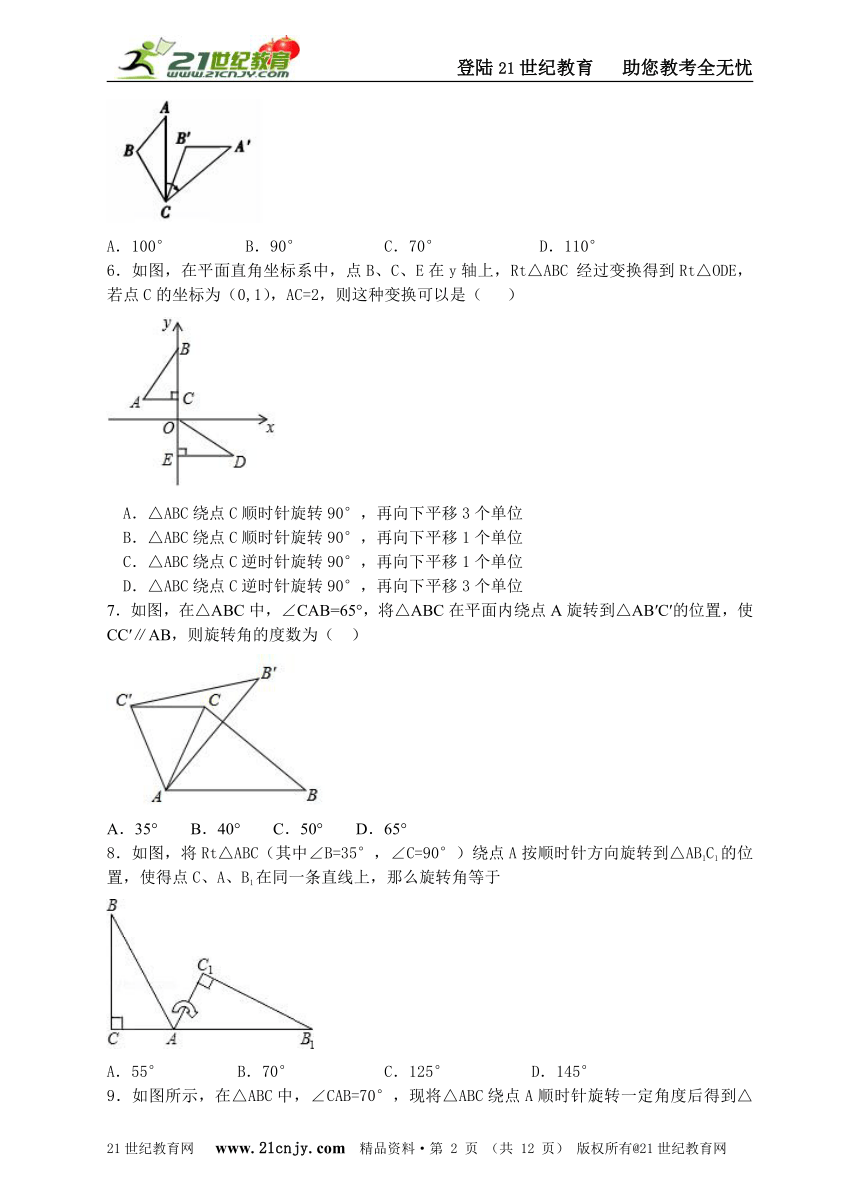
5.如图,将△ABC绕着点C顺时针旋转60°后得到△A?B?C,若∠A=40°,∠B=110°,则∠BCA?的度数是( )2-1-c-n-j-y
A.100° B.90° C.70° D.110°
6.如图,在平面直角坐标系中,点B、C、E在y轴上,Rt△ABC 经过变换得到Rt△ODE,若点C的坐标为(0,1),AC=2,则这种变换可以是( )21·世纪*教育网
A.△ABC绕点C顺时针旋转90°,再向下平移3个单位
B.△ABC绕点C顺时针旋转90°,再向下平移1个单位
C.△ABC绕点C逆时针旋转90°,再向下平移1个单位
D.△ABC绕点C逆时针旋转90°,再向下平移3个单位
7.如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )【来源:21cnj*y.co*m】
A.35° B.40° C.50° D.65°
8.如图,将Rt△ABC(其中∠B=35°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么旋转角等于【出处:21教育名师】
A.55° B.70° C.125° D.145°
9.如图所示,在△ABC中,∠CAB=70°,现将△ABC绕点A顺时针旋转一定角度后得到△AB′C′,连接BB′,若BB′∥AC′,则∠CAB′的度数为( )21教育名师原创作品
A.20° B.25° C.30° D.40°
10.如图,将等腰直角三角形ABC绕点A逆时针旋转15°后得到△AB′C′,若AC=1,则图中阴影部分的面积为( )21*cnjy*com
A. B. C. D.
二、填空题:(每小题3分共30分)
11.等边三角形至少旋转 度才能与自身重合.
12.如图,将△ABC绕点A按顺时针方向旋转60°得△ADE,则∠BAD= 度.
13.如图,在Rt△OAB中,∠AOB=30°,将△OAB绕点O逆时针旋转100°得到△OA1B1,则∠A1OB= °.【版权所有:21教育】
14.在平面直角坐标系中,线段AB的端点A的坐标为(-3,2),将其先向右平移4个单位,再向下平移3个单位,得到线段A′B′,则点A对应点A′的坐标为 .
15.已知一副直角三角板如图放置,其中BC=3,EF=4,把30°的三角板向右平移,使顶点B落在45°的三角板的斜边DF上,则两个三角板重叠部分(阴影部分)的面积为 .
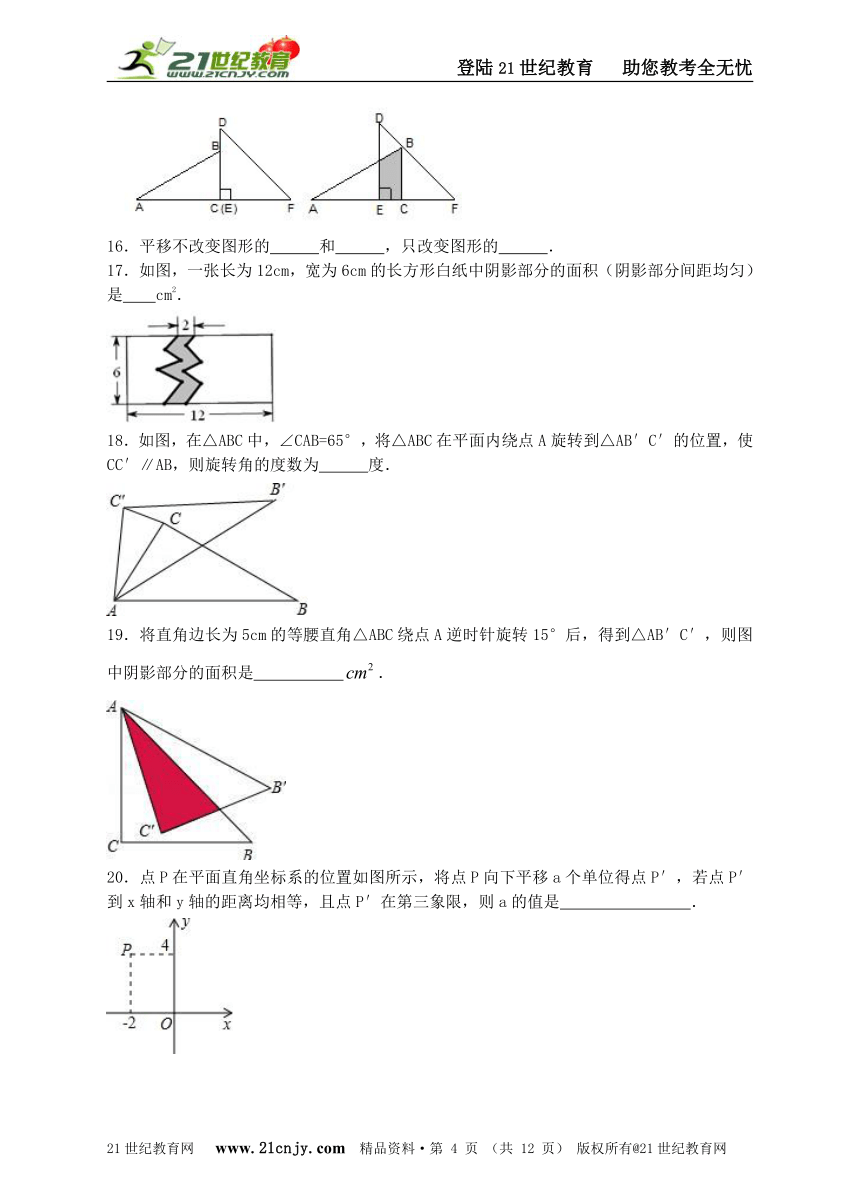
16.平移不改变图形的 和 ,只改变图形的 .
17.如图,一张长为12cm,宽为6cm的长方形白纸中阴影部分的面积(阴影部分间距均匀)是 cm2.
18.如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为 度.【来源:21·世纪·教育·网】
19.将直角边长为5cm的等腰直角△ABC绕点A逆时针旋转15°后,得到△AB′C′,则图中阴影部分的面积是 .
20.点P在平面直角坐标系的位置如图所示,将点P向下平移a个单位得点P′,若点P′到x轴和y轴的距离均相等,且点P′在第三象限,则a的值是 .
三、解答题:(共40分)
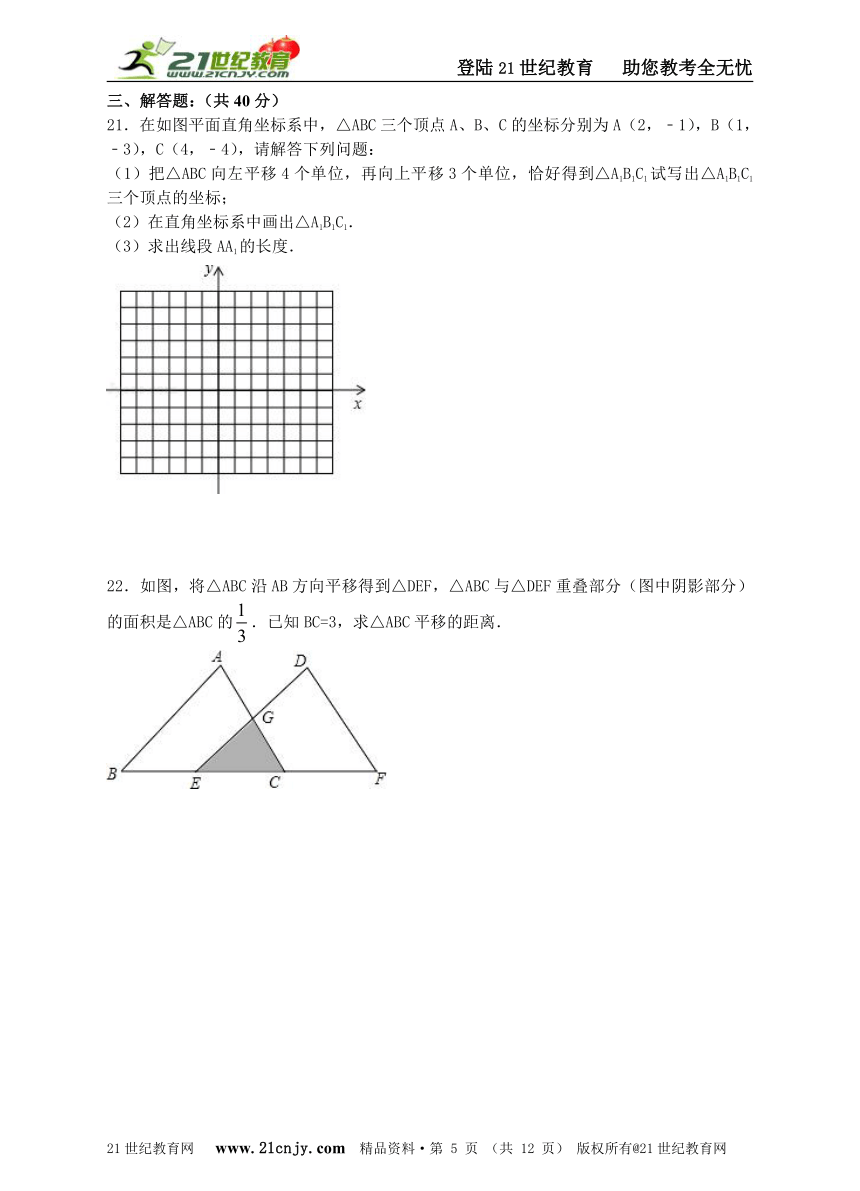
21.在如图平面直角坐标系中,△ABC三个顶点A、B、C的坐标分别为A(2,﹣1),B(1,﹣3),C(4,﹣4),请解答下列问题:
(1)把△ABC向左平移4个单位,再向上平移3个单位,恰好得到△A1B1C1试写出△A1B1C1三个顶点的坐标;
(2)在直角坐标系中画出△A1B1C1.
(3)求出线段AA1的长度.
22.如图,将△ABC沿AB方向平移得到△DEF,△ABC与△DEF重叠部分(图中阴影部分)的面积是△ABC的.已知BC=3,求△ABC平移的距离. 21世纪教育网版权所有
23.如图,在平面直角坐标系中,O为坐标原点,每个小方格的边长为1个单位长度.正方形ABCD顶点都在格点上,其中,点A的坐标为(1,1).
(1)将正方形ABCD绕点A顺时针方向旋转90°画出旋转后的图形;
(2)若点B到达点,点C到达点,点D到达点,写出点、、的坐标.
24.如图,等腰Rt△ABC中,BA=BC,∠ABC=90°,点D在AC上,将△ABD绕点B沿顺时针方向旋转90°后,得到△CBE.
(1)求∠DCE的度数;
(2)若AB=4,CD=3AD,求DE的长.
参考答案
1.C
【解析】
试题分析:根据平移的性质,一个图形延某个方向移动一定的距离,可得答案为C.
故选:C
2.A.
【解析】
试题分析:观察图象,发现平移前后,B、E对应,C、F对应,根据平移的性质,易得平移的距离=BE=5﹣3=2.21·cn·jy·com
故选:A.
3.D
【解析】解:A、荡秋千不符合平移的性质,不属于平移,故本选项错误;
B、地球绕着太阳转不符合平移的性质,不属于平移,故本选项错误;
C、风筝在空中随风飘动,不符合平移的性质,故本选项错误;
D、急刹车时,汽车在地面上的滑动,符合平移的性质,故本选项正确.
故选D.
4.C.
【解析】
试题解析:如图,连接AA′、BB′.
∵点A的坐标为(0,3),△OAB沿x轴向右平移后得到△O′A′B′,
∴点A′的纵坐标是3.
又∵点A的对应点在直线y=x上一点,
∴3=x,解得x=4.
∴点A′的坐标是(4,3),
∴AA′=4.
∴根据平移的性质知BB′=AA′=4.
故选C.
5.B
【解析】
试题分析:根据三角形内角和定理可得∠ACB=30°,根据旋转的性质可得∠ACA′=60°,则∠BCA′=90°.21cnjy.com
6.A.
【解析】
试题解析:根据图形可以看出,△ABC绕点C顺时针旋转90°,再向下平移3个单位可以得到△ODE.
故选A.
7.C.
【解析】
试题分析:∵CC′∥AB,∴∠ACC′=∠CAB=65°,∵△ABC绕点A旋转得到△AB′C′,∴AC=AC′,∴∠CAC′=180°﹣2∠ACC′=180°﹣2×65°=50°,∴∠CAC′=∠BAB′=50°.故选C.
8.C
【解析】
试题分析:根据题意可知:∠是旋转角,因为在Rt△ABC中∠B=35°,∠C=90°,所以∠BAC=90°-35°=55°,所以∠=180°-55°=125°,故选:C.
9.C.
【解析】
试题分析:由旋转的性质得:∠C′AB′=∠CAB=70°,AB′=AB,∴∠AB′B=∠ABB′,∵BB′∥AC′,∴∠AB′B=∠C′AB′=70°,∴∠ABB′=70°,∴∠BAB′=180°﹣70°﹣70°=40°,∴∠CAB′=∠CAB﹣∠BAB′=70°﹣40°=30°;故选C.
10.B.
【解析】
试题分析:根据题意,AC′=AC=1,
∵∠B′AB=15°,
∴∠BAC′=45°﹣15°=30°,
∴C′D=AC′tan30°=,
∴S阴影=AC′?C′D=×1×=.
故选B.
11.120度
【解析】
试题分析:等边三角形的中心到三个顶点的距离相等,相邻顶点与中心连线的夹角相等,求旋转角即可.
解:因为等边三角形的中心到三个顶点的距离相等,相邻顶点与中心连线的夹角相等,
所以,旋转角为360°÷3=120°,故至少旋转120度才能与自身重合.
12.60.
【解析】
试题分析:∵将△ABC绕点A按顺时针方向旋转60°得△ADE,∴∠BAD=60度.故答案为:60.
13.70.
【解析】
试题分析:根据旋转的性质可知,∠A1OA=100°,因为∠AOB=30°,所以∠A1OB=100°-30°=70°.www-2-1-cnjy-com
故答案为:70.
14.(1,-1).
【解析】
试题解析:将点A(-3,2)向右平移4个单位,再向下平移3个单位,
即把A点的横坐标加4,纵坐标减3即可,即A′的坐标为(1,-1).
15.3-
【解析】
试题分析:根据题意可得AB=2BC=6,AC=3,则△ABC的面积=,设DE与AB的交点为点H,根据平移可得CF=BC=3,则EC=1,AE=3-1,EH=3-,△AEH的面积=-3,所以阴影部分的面积=△ABC的面积-△AEH的面积=-(-3)=3-.
16.形状和大小,位置
【解析】
试题分析:根据平移的性质,可直接得到正确答案.
解:平移不改变图形的形状和大小,只改变图形的位置.
17.12.
【解析】
试题分析:如图,平移后得一个矩形,一边长为2,另一边长为6,所以面积是12.
18.50
【解析】
试题分析:根据两直线平行,内错角相等可得∠ACC′=∠CAB,根据旋转的性质可得AC=AC′,然后利用等腰三角形两底角相等求∠CAC′,再根据∠CAC′、∠BAB′都是旋转角解答.
解:如图,∵CC′∥AB,
∴∠ACC′=∠CAB=65°,
∵△ABC绕点A旋转得到△AB′C′,
∴AC=AC′,
∴∠CAC′=180°﹣2∠ACC′=180°﹣2×65°=50°,
∴∠CAC′=∠BAB′=50°
故答案为:50.
19..
【解析】
试题分析:由旋转的性质可得,阴影部分为直角三角形,且∠C′AB=∠CAB﹣∠CAC′=45°﹣15°=30°,AC′=AC=5,所以阴影部分的面积=×5×tan30°×5=.
故答案为:.
20.6.
【解析】
试题解析:由图得知:P(-2,4),
∵将点P向下平移a个单位得点P′,
∴P′(-2,4-a),
∵点P′到x轴和y轴的距离均相等,且点P′在第三象限,
∴4-a=-2,
∴a=6
21.(1)如图,A1(﹣2,2),B1(﹣3,0),C1(0,﹣1);
(2)如图所示,△A1B1C1即为所求作的三角形;
(3)AA1==5.
【解析】
试题分析:(1)先描出点A、B、C得到△ABC,再根据平移结合平面直角坐标系写出△A1B1C1三个顶点的坐标;2·1·c·n·j·y
(2)根据网格结构找出点A、B、C的对应点A1、B1、C1的位置,然后顺次连接即可;
(3)根据网格结构,找出AA1所在的直角三角形的直角边的长度,然后利用勾股定理列式计算即可得解.
解:(1)如图,A1(﹣2,2),B1(﹣3,0),C1(0,﹣1);
(2)如图所示,△A1B1C1即为所求作的三角形;
(3)AA1==5.
22.3-.
【解析】
试题分析:移动的距离可以视为FC或BE的长度,根据题意可知△ABC与阴影部分为相似三角形,且面积比为3: 1,所以BC:EC=:1,推出EC=,所以BE=3-.
试题解析:∵△ABC沿AB边平移到△DEF的位置,
∴AC∥DF,
∴△ABC∽△DBG,
∴
∴BC:EC=3:1,
∵BC=3,
∴EC=,
∴△ABC平移的距离为:BE=3-.
23.(1)作图详见解析;(2)(2,﹣1),(4,0),(3,2).
【解析】
试题分析:(1)分别画出B、C、D三点绕点A顺时针方向旋转90°后的对应点、、即可;
(2)根据图象写出坐标即可.
试题解析:(1)正方形ABCD绕点A顺时针方向旋转90°,旋转后的图形如图所示.
(2)(2,﹣1),(4,0),(3,2).
24.(1) 90°.(2)
【解析】
试题分析:(1)首先由等腰直角三角形的性质求得∠BAD、∠BCD的度数,然后由旋转的性质可求得∠BCE的度数,故此可求得∠DCE的度数;www.21-cn-jy.com
(2)由(1)可知△DCE是直角三角形,先由勾股定理求得AC的长,然后依据比例关系可得到CE和DC的长,最后依据勾股定理求解即可.21*cnjy*com
试题解析:(1)∵△ABCD为等腰直角三角形,
∴∠BAD=∠BCD=45°.
由旋转的性质可知∠BAD=∠BCE=45°.
∴∠DCE=∠BCE+∠BCA=45°+45°=90°.
(2)∵BA=BC,∠ABC=90°,
∴AC=.
∵CD=3AD,
∴AD=,DC=3.
由旋转的性质可知:AD=EC=.
∴DE=.
第 5周测试卷
(测试范围:3.1图形的平移——3.2图形的旋转)
班级:___________ 姓名:___________ 得分:___________
一、选择题:(每小题3分共30分)
1. 观察下面图案,在A、B、C、D四幅图案中,能通过图案(1)的平移得到的是( )
2.如图,△ABC沿着由点B到点E的方向,平移到△DEF,已知BC=5.EC=3,那么平移的距离为( ).21教育网
A.2 B.3 C.5 D.7
3.下列运动属于平移的是( )
A.荡秋千
B.地球绕着太阳转
C.风筝在空中随风飘动
D.急刹车时,汽车在地面上的滑动
4.如图,在平面直角坐标系中,点A的坐标为(0,3),△OAB沿x轴向右平移后得到△O′A′B′,点A的对应点在直线y=x上一点,则点B与其对应点B′间的距离为( )
A. B.3 C.4 D.5
5.如图,将△ABC绕着点C顺时针旋转60°后得到△A?B?C,若∠A=40°,∠B=110°,则∠BCA?的度数是( )2-1-c-n-j-y
A.100° B.90° C.70° D.110°
6.如图,在平面直角坐标系中,点B、C、E在y轴上,Rt△ABC 经过变换得到Rt△ODE,若点C的坐标为(0,1),AC=2,则这种变换可以是( )21·世纪*教育网
A.△ABC绕点C顺时针旋转90°,再向下平移3个单位
B.△ABC绕点C顺时针旋转90°,再向下平移1个单位
C.△ABC绕点C逆时针旋转90°,再向下平移1个单位
D.△ABC绕点C逆时针旋转90°,再向下平移3个单位
7.如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )【来源:21cnj*y.co*m】
A.35° B.40° C.50° D.65°
8.如图,将Rt△ABC(其中∠B=35°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么旋转角等于【出处:21教育名师】
A.55° B.70° C.125° D.145°
9.如图所示,在△ABC中,∠CAB=70°,现将△ABC绕点A顺时针旋转一定角度后得到△AB′C′,连接BB′,若BB′∥AC′,则∠CAB′的度数为( )21教育名师原创作品
A.20° B.25° C.30° D.40°
10.如图,将等腰直角三角形ABC绕点A逆时针旋转15°后得到△AB′C′,若AC=1,则图中阴影部分的面积为( )21*cnjy*com
A. B. C. D.
二、填空题:(每小题3分共30分)
11.等边三角形至少旋转 度才能与自身重合.
12.如图,将△ABC绕点A按顺时针方向旋转60°得△ADE,则∠BAD= 度.
13.如图,在Rt△OAB中,∠AOB=30°,将△OAB绕点O逆时针旋转100°得到△OA1B1,则∠A1OB= °.【版权所有:21教育】
14.在平面直角坐标系中,线段AB的端点A的坐标为(-3,2),将其先向右平移4个单位,再向下平移3个单位,得到线段A′B′,则点A对应点A′的坐标为 .
15.已知一副直角三角板如图放置,其中BC=3,EF=4,把30°的三角板向右平移,使顶点B落在45°的三角板的斜边DF上,则两个三角板重叠部分(阴影部分)的面积为 .
16.平移不改变图形的 和 ,只改变图形的 .
17.如图,一张长为12cm,宽为6cm的长方形白纸中阴影部分的面积(阴影部分间距均匀)是 cm2.
18.如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为 度.【来源:21·世纪·教育·网】
19.将直角边长为5cm的等腰直角△ABC绕点A逆时针旋转15°后,得到△AB′C′,则图中阴影部分的面积是 .
20.点P在平面直角坐标系的位置如图所示,将点P向下平移a个单位得点P′,若点P′到x轴和y轴的距离均相等,且点P′在第三象限,则a的值是 .
三、解答题:(共40分)
21.在如图平面直角坐标系中,△ABC三个顶点A、B、C的坐标分别为A(2,﹣1),B(1,﹣3),C(4,﹣4),请解答下列问题:
(1)把△ABC向左平移4个单位,再向上平移3个单位,恰好得到△A1B1C1试写出△A1B1C1三个顶点的坐标;
(2)在直角坐标系中画出△A1B1C1.
(3)求出线段AA1的长度.
22.如图,将△ABC沿AB方向平移得到△DEF,△ABC与△DEF重叠部分(图中阴影部分)的面积是△ABC的.已知BC=3,求△ABC平移的距离. 21世纪教育网版权所有
23.如图,在平面直角坐标系中,O为坐标原点,每个小方格的边长为1个单位长度.正方形ABCD顶点都在格点上,其中,点A的坐标为(1,1).
(1)将正方形ABCD绕点A顺时针方向旋转90°画出旋转后的图形;
(2)若点B到达点,点C到达点,点D到达点,写出点、、的坐标.
24.如图,等腰Rt△ABC中,BA=BC,∠ABC=90°,点D在AC上,将△ABD绕点B沿顺时针方向旋转90°后,得到△CBE.
(1)求∠DCE的度数;
(2)若AB=4,CD=3AD,求DE的长.
参考答案
1.C
【解析】
试题分析:根据平移的性质,一个图形延某个方向移动一定的距离,可得答案为C.
故选:C
2.A.
【解析】
试题分析:观察图象,发现平移前后,B、E对应,C、F对应,根据平移的性质,易得平移的距离=BE=5﹣3=2.21·cn·jy·com
故选:A.
3.D
【解析】解:A、荡秋千不符合平移的性质,不属于平移,故本选项错误;
B、地球绕着太阳转不符合平移的性质,不属于平移,故本选项错误;
C、风筝在空中随风飘动,不符合平移的性质,故本选项错误;
D、急刹车时,汽车在地面上的滑动,符合平移的性质,故本选项正确.
故选D.
4.C.
【解析】
试题解析:如图,连接AA′、BB′.
∵点A的坐标为(0,3),△OAB沿x轴向右平移后得到△O′A′B′,
∴点A′的纵坐标是3.
又∵点A的对应点在直线y=x上一点,
∴3=x,解得x=4.
∴点A′的坐标是(4,3),
∴AA′=4.
∴根据平移的性质知BB′=AA′=4.
故选C.
5.B
【解析】
试题分析:根据三角形内角和定理可得∠ACB=30°,根据旋转的性质可得∠ACA′=60°,则∠BCA′=90°.21cnjy.com
6.A.
【解析】
试题解析:根据图形可以看出,△ABC绕点C顺时针旋转90°,再向下平移3个单位可以得到△ODE.
故选A.
7.C.
【解析】
试题分析:∵CC′∥AB,∴∠ACC′=∠CAB=65°,∵△ABC绕点A旋转得到△AB′C′,∴AC=AC′,∴∠CAC′=180°﹣2∠ACC′=180°﹣2×65°=50°,∴∠CAC′=∠BAB′=50°.故选C.
8.C
【解析】
试题分析:根据题意可知:∠是旋转角,因为在Rt△ABC中∠B=35°,∠C=90°,所以∠BAC=90°-35°=55°,所以∠=180°-55°=125°,故选:C.
9.C.
【解析】
试题分析:由旋转的性质得:∠C′AB′=∠CAB=70°,AB′=AB,∴∠AB′B=∠ABB′,∵BB′∥AC′,∴∠AB′B=∠C′AB′=70°,∴∠ABB′=70°,∴∠BAB′=180°﹣70°﹣70°=40°,∴∠CAB′=∠CAB﹣∠BAB′=70°﹣40°=30°;故选C.
10.B.
【解析】
试题分析:根据题意,AC′=AC=1,
∵∠B′AB=15°,
∴∠BAC′=45°﹣15°=30°,
∴C′D=AC′tan30°=,
∴S阴影=AC′?C′D=×1×=.
故选B.
11.120度
【解析】
试题分析:等边三角形的中心到三个顶点的距离相等,相邻顶点与中心连线的夹角相等,求旋转角即可.
解:因为等边三角形的中心到三个顶点的距离相等,相邻顶点与中心连线的夹角相等,
所以,旋转角为360°÷3=120°,故至少旋转120度才能与自身重合.
12.60.
【解析】
试题分析:∵将△ABC绕点A按顺时针方向旋转60°得△ADE,∴∠BAD=60度.故答案为:60.
13.70.
【解析】
试题分析:根据旋转的性质可知,∠A1OA=100°,因为∠AOB=30°,所以∠A1OB=100°-30°=70°.www-2-1-cnjy-com
故答案为:70.
14.(1,-1).
【解析】
试题解析:将点A(-3,2)向右平移4个单位,再向下平移3个单位,
即把A点的横坐标加4,纵坐标减3即可,即A′的坐标为(1,-1).
15.3-
【解析】
试题分析:根据题意可得AB=2BC=6,AC=3,则△ABC的面积=,设DE与AB的交点为点H,根据平移可得CF=BC=3,则EC=1,AE=3-1,EH=3-,△AEH的面积=-3,所以阴影部分的面积=△ABC的面积-△AEH的面积=-(-3)=3-.
16.形状和大小,位置
【解析】
试题分析:根据平移的性质,可直接得到正确答案.
解:平移不改变图形的形状和大小,只改变图形的位置.
17.12.
【解析】
试题分析:如图,平移后得一个矩形,一边长为2,另一边长为6,所以面积是12.
18.50
【解析】
试题分析:根据两直线平行,内错角相等可得∠ACC′=∠CAB,根据旋转的性质可得AC=AC′,然后利用等腰三角形两底角相等求∠CAC′,再根据∠CAC′、∠BAB′都是旋转角解答.
解:如图,∵CC′∥AB,
∴∠ACC′=∠CAB=65°,
∵△ABC绕点A旋转得到△AB′C′,
∴AC=AC′,
∴∠CAC′=180°﹣2∠ACC′=180°﹣2×65°=50°,
∴∠CAC′=∠BAB′=50°
故答案为:50.
19..
【解析】
试题分析:由旋转的性质可得,阴影部分为直角三角形,且∠C′AB=∠CAB﹣∠CAC′=45°﹣15°=30°,AC′=AC=5,所以阴影部分的面积=×5×tan30°×5=.
故答案为:.
20.6.
【解析】
试题解析:由图得知:P(-2,4),
∵将点P向下平移a个单位得点P′,
∴P′(-2,4-a),
∵点P′到x轴和y轴的距离均相等,且点P′在第三象限,
∴4-a=-2,
∴a=6
21.(1)如图,A1(﹣2,2),B1(﹣3,0),C1(0,﹣1);
(2)如图所示,△A1B1C1即为所求作的三角形;
(3)AA1==5.
【解析】
试题分析:(1)先描出点A、B、C得到△ABC,再根据平移结合平面直角坐标系写出△A1B1C1三个顶点的坐标;2·1·c·n·j·y
(2)根据网格结构找出点A、B、C的对应点A1、B1、C1的位置,然后顺次连接即可;
(3)根据网格结构,找出AA1所在的直角三角形的直角边的长度,然后利用勾股定理列式计算即可得解.
解:(1)如图,A1(﹣2,2),B1(﹣3,0),C1(0,﹣1);
(2)如图所示,△A1B1C1即为所求作的三角形;
(3)AA1==5.
22.3-.
【解析】
试题分析:移动的距离可以视为FC或BE的长度,根据题意可知△ABC与阴影部分为相似三角形,且面积比为3: 1,所以BC:EC=:1,推出EC=,所以BE=3-.
试题解析:∵△ABC沿AB边平移到△DEF的位置,
∴AC∥DF,
∴△ABC∽△DBG,
∴
∴BC:EC=3:1,
∵BC=3,
∴EC=,
∴△ABC平移的距离为:BE=3-.
23.(1)作图详见解析;(2)(2,﹣1),(4,0),(3,2).
【解析】
试题分析:(1)分别画出B、C、D三点绕点A顺时针方向旋转90°后的对应点、、即可;
(2)根据图象写出坐标即可.
试题解析:(1)正方形ABCD绕点A顺时针方向旋转90°,旋转后的图形如图所示.
(2)(2,﹣1),(4,0),(3,2).
24.(1) 90°.(2)
【解析】
试题分析:(1)首先由等腰直角三角形的性质求得∠BAD、∠BCD的度数,然后由旋转的性质可求得∠BCE的度数,故此可求得∠DCE的度数;www.21-cn-jy.com
(2)由(1)可知△DCE是直角三角形,先由勾股定理求得AC的长,然后依据比例关系可得到CE和DC的长,最后依据勾股定理求解即可.21*cnjy*com
试题解析:(1)∵△ABCD为等腰直角三角形,
∴∠BAD=∠BCD=45°.
由旋转的性质可知∠BAD=∠BCE=45°.
∴∠DCE=∠BCE+∠BCA=45°+45°=90°.
(2)∵BA=BC,∠ABC=90°,
∴AC=.
∵CD=3AD,
∴AD=,DC=3.
由旋转的性质可知:AD=EC=.
∴DE=.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
