2017湘教版八年级数学下册期中测试(含答案)
文档属性
| 名称 | 2017湘教版八年级数学下册期中测试(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 380.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-12 10:03:59 | ||
图片预览

文档简介
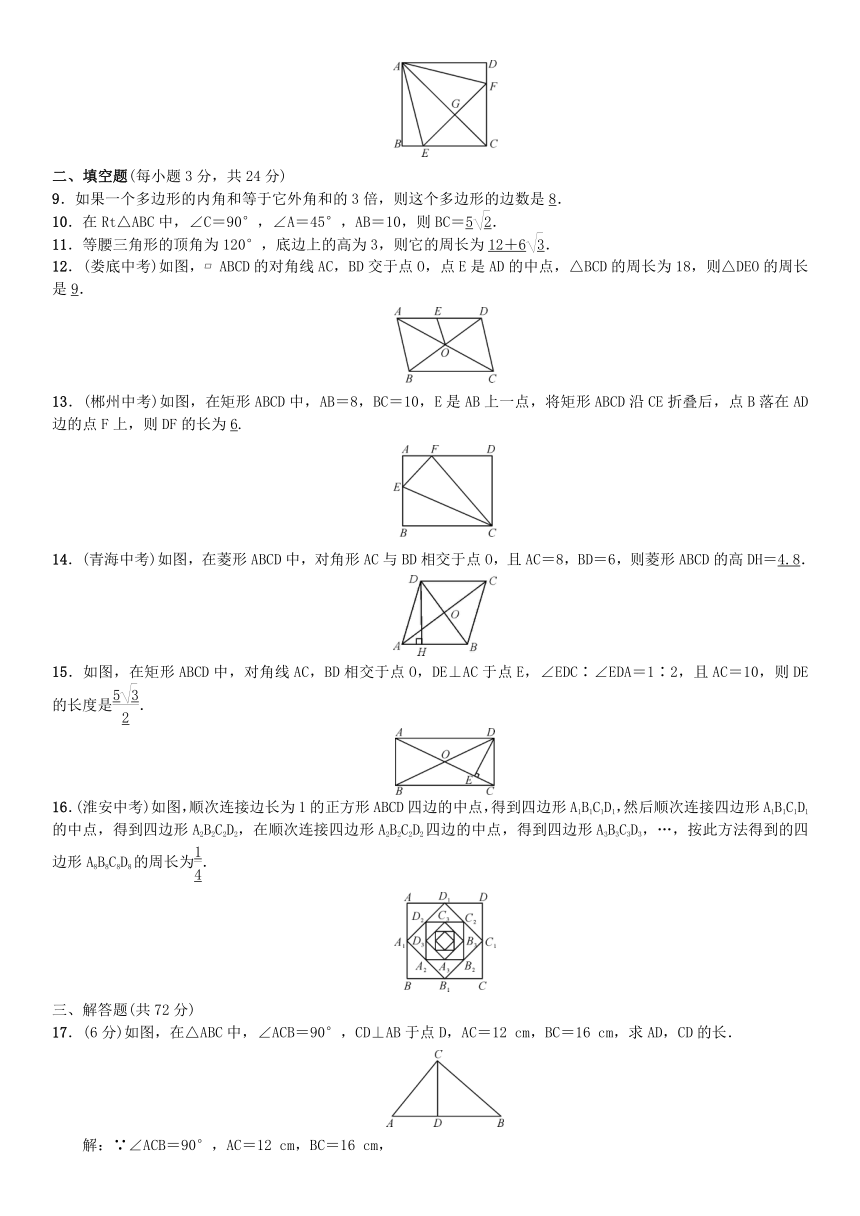
期中测试
(时间:90分钟 满分:120分)
题号
一
二
三
总分
合分人
复分人
得分
一、选择题(每小题3分,共24分)
1.在一个直角三角形中,有一个锐角等于60°,则另一个锐角的度数是(D)
A.75°
B.60°
C.45°
D.30°
2.(天水中考)下列汽车标志中既是轴对称图形又是中心对称图形的是(C)
,A) ,B) ,C) ,D)
3.(重庆B卷)如图,在矩形ABCD中,对角线AC,BD相交于点O,∠ACB=30°,则∠AOB的大小为(B)
A.30°
B.60°
C.90°
D.120°
4.在△ABC内部取一点P,使得点P到△ABC的三边距离相等,则点P应是△ABC的哪三条线的交点(B)
A.高
B.角平分线
C.中线
D.三边的垂直平分线
5.如图,四边形ABCD是菱形,过点A作BD的平行线交CD的延长线于点E,则下列式子不成立的是(B)
A.DA=DE
B.BD=CE
C.∠EAC=90°
D.∠ABC=2∠E
6.如图,一个梯子AB长2.5米,顶端A靠在墙AC上,这时梯子下端B与墙角C距离为1.5米,梯子滑动后停在DE的位置上,测得BD长为0.5米,则梯子顶端A下落了(A)
A.0.5米
B.1米
C.1.5米
D.2米
7.(眉山中考)如图,在Rt△ABC中,∠B=90°,∠A=30°,DE垂直平分斜边AC,交AB于D,E是垂足,连接CD.若BD=1,则AC的长是(A)
A.2
B.2
C.4
D.4
8.如图,在正方形ABCD中,点E,F分别在BC,CD上,△AEF是等边三角形,连接AC交EF于点G,下列结论:①BE=DF;②∠DAF=15°;③AC垂直平分EF;④BE+DF=EF;⑤S△CEF=2S△ABE.其中正确结论的个数为(C)
A.2
B.3
C.4
D.5
二、填空题(每小题3分,共24分)
9.如果一个多边形的内角和等于它外角和的3倍,则这个多边形的边数是8.
10.在Rt△ABC中,∠C=90°,∠A=45°,AB=10,则BC=5.
11.等腰三角形的顶角为120°,底边上的高为3,则它的周长为12+6.
12.(娄底中考)如图, ABCD的对角线AC,BD交于点O,点E是AD的中点,△BCD的周长为18,则△DEO的周长是9.
13.(郴州中考)如图,在矩形ABCD中,AB=8,BC=10,E是AB上一点,将矩形ABCD沿CE折叠后,点B落在AD边的点F上,则DF的长为6.
14.(青海中考)如图,在菱形ABCD中,对角形AC与BD相交于点O,且AC=8,BD=6,则菱形ABCD的高DH=4.8.
15.如图,在矩形ABCD中,对角线AC,BD相交于点O,DE⊥AC于点E,∠EDC∶∠EDA=1∶2,且AC=10,则DE的长度是.
16.(淮安中考)如图,顺次连接边长为1的正方形ABCD四边的中点,得到四边形A1B1C1D1,然后顺次连接四边形A1B1C1D1的中点,得到四边形A2B2C2D2,在顺次连接四边形A2B2C2D2四边的中点,得到四边形A3B3C3D3,…,按此方法得到的四边形A8B8C8D8的周长为.
三、解答题(共72分)
17.(6分)如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,AC=12
cm,BC=16
cm,求AD,CD的长.
解:∵∠ACB=90°,AC=12
cm,BC=16
cm,
∴AB=20
cm.
根据直角三角形的面积公式,得CD==9.6
cm.
在Rt△ACD中,AD==7.2
cm.
18.(6分)如图,在四边形ABCD中,E,F,G,H分别是AD,BD,BC,AC上的中点,AB=5,CD=7.求四边形EFGH的周长.
解:∵E,F,G,H分别是AD,BD,BC,AC上的中点,AB=5,CD=7.
∴EF∥AB∥GH,EH∥CD∥FG,EF=2.5,EH=3.5.
∴四边形EFGH为平行四边形.
∴四边形EFGH的周长为2(EF+EH)=2×6=12.
19.(8分)(益阳中考)如图,在 ABCD中,AE⊥BD于点E,CF⊥BD于点F,连接AF,CE.求证:AF=CE.
证明:∵四边形ABCD是平行四边形,
∴AD=BC,∠ADB=∠CBD.
又∵AE⊥BD,CF⊥BD,
∴∠AED=∠CFB,AE∥CF.
∴△AED≌△CFB(AAS).
∴AE=CF.
∴四边形AECF是平行四边形.
∴AF=CE.
20.(10分)如图,点P是∠MON中一点,PA⊥OM于点A,PB⊥ON于点B,连接AB,∠PAB=∠PBA.
(1)求证:OP平分∠MON;
(2)若∠MON=80°,求∠PAB的度数.
解:(1)证明:∵∠PAB=∠PBA,
∴PA=PB.
∵PA⊥OM,PB⊥ON,
∴OP平分∠MON.
(2)∵∠MON=80°,PA⊥OM,PB⊥ON,
∴∠APB=360°-90°×2-80°=100°.
∵∠PAB=∠PBA,
∴∠PAB=×(180°-100°)=40°.
21.(10分)(眉山中考)如图,在方格网中已知格点△ABC和点O.
(1)画△A′B′C′和△ABC关于点O成中心对称;
(2)请在方格网中标出所有使以点A,O,C′,D为顶点的四边形是平行四边形的D点.
解:(1)如图所示.
(2)根据题意画图如下:
22.(10分)(雅安中考)如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE.连接DE.
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.
解:(1)证明:∵△BAD是由△BEC绕点B旋转60°而得,
∴DB=CB,∠ABD=∠EBC,∠ABE=60°.
又∵AB⊥BC,∴∠ABC=90°.∴∠DBE=∠CBE=30°.
在△BDE和△BCE中,∴△BDE≌△BCE(SAS).
(2)四边形ABED是菱形.理由:由(1)得△BDE≌△BCE.
又∵△BAD是由△BEC旋转得到,∴△BAD≌△BEC.
∴BA=BE,AD=ED=EC.又∵BE=CE,∴AB=BE=ED=DA.
∴四边形ABED是菱形.
23.(10分)如图,P是正方形ABCD对角线AC上一点,点E在BC上,且PE=PB.
(1)求证:PE=PD;
(2)连接DE,试求∠PED的度数.
解:(1)证明:∵四边形ABCD是正方形,
∴BC=CD,∠ACB=∠ACD,
在△PBC和△PDC中,
∴△PBC≌△PDC(SAS).
∴PB=PD.
∵PE=PB.
∴PE=PD.
(2)∵四边形ABCD是正方形,
∴∠BCD=90°.
∵△PBC≌△PDC,
∴∠PBC=∠PDC.
∵PE=PB,
∴∠PBC=∠PEB.
∴∠PDC=∠PEB.
∵∠PEB+∠PEC=180°,
∴∠PDC+∠PEC=180°.
在四边形PECD中,∠EPD=360°-
(∠PDC+∠PEC)-∠BCD=360°-180°-90°=90°,
又∵PE=PD,
∴△PDE是等腰直角三角形.
∴∠PED=45°.
24.(12分)(兰州中考)给出定义,若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称该四边形为勾股四边形.
(1)在你学过的特殊四边形中,写出两种勾股四边形的名称;
(2)如图,将△ABC绕顶点B按顺时针方向旋转60°得到△DBE,连接AD,DC,CE,已知:∠DCB=30°.
①求证:△BCE是等边三角形;
②求证:DC2+BC2=AC2,即四边形ABCD是勾股四边形.
解:(1)正方形、矩形.
(2)证明:①由旋转的性质得△ABC≌△DBE,
∴BC=BE.
∵∠CBE=60°,∴△BCE是等边三角形.
②∵△ABC≌△DBE,
∴BE=BC,AC=DE.
∵△BCE为等边三角形,
∴BC=CE,∠BCE=60°.
∵∠DCB=30°,∴∠DCE=90°.
在Rt△DCE中,DC2+CE2=DE2,
∴DC2+BC2=AC2.
(时间:90分钟 满分:120分)
题号
一
二
三
总分
合分人
复分人
得分
一、选择题(每小题3分,共24分)
1.在一个直角三角形中,有一个锐角等于60°,则另一个锐角的度数是(D)
A.75°
B.60°
C.45°
D.30°
2.(天水中考)下列汽车标志中既是轴对称图形又是中心对称图形的是(C)
,A) ,B) ,C) ,D)
3.(重庆B卷)如图,在矩形ABCD中,对角线AC,BD相交于点O,∠ACB=30°,则∠AOB的大小为(B)
A.30°
B.60°
C.90°
D.120°
4.在△ABC内部取一点P,使得点P到△ABC的三边距离相等,则点P应是△ABC的哪三条线的交点(B)
A.高
B.角平分线
C.中线
D.三边的垂直平分线
5.如图,四边形ABCD是菱形,过点A作BD的平行线交CD的延长线于点E,则下列式子不成立的是(B)
A.DA=DE
B.BD=CE
C.∠EAC=90°
D.∠ABC=2∠E
6.如图,一个梯子AB长2.5米,顶端A靠在墙AC上,这时梯子下端B与墙角C距离为1.5米,梯子滑动后停在DE的位置上,测得BD长为0.5米,则梯子顶端A下落了(A)
A.0.5米
B.1米
C.1.5米
D.2米
7.(眉山中考)如图,在Rt△ABC中,∠B=90°,∠A=30°,DE垂直平分斜边AC,交AB于D,E是垂足,连接CD.若BD=1,则AC的长是(A)
A.2
B.2
C.4
D.4
8.如图,在正方形ABCD中,点E,F分别在BC,CD上,△AEF是等边三角形,连接AC交EF于点G,下列结论:①BE=DF;②∠DAF=15°;③AC垂直平分EF;④BE+DF=EF;⑤S△CEF=2S△ABE.其中正确结论的个数为(C)
A.2
B.3
C.4
D.5
二、填空题(每小题3分,共24分)
9.如果一个多边形的内角和等于它外角和的3倍,则这个多边形的边数是8.
10.在Rt△ABC中,∠C=90°,∠A=45°,AB=10,则BC=5.
11.等腰三角形的顶角为120°,底边上的高为3,则它的周长为12+6.
12.(娄底中考)如图, ABCD的对角线AC,BD交于点O,点E是AD的中点,△BCD的周长为18,则△DEO的周长是9.
13.(郴州中考)如图,在矩形ABCD中,AB=8,BC=10,E是AB上一点,将矩形ABCD沿CE折叠后,点B落在AD边的点F上,则DF的长为6.
14.(青海中考)如图,在菱形ABCD中,对角形AC与BD相交于点O,且AC=8,BD=6,则菱形ABCD的高DH=4.8.
15.如图,在矩形ABCD中,对角线AC,BD相交于点O,DE⊥AC于点E,∠EDC∶∠EDA=1∶2,且AC=10,则DE的长度是.
16.(淮安中考)如图,顺次连接边长为1的正方形ABCD四边的中点,得到四边形A1B1C1D1,然后顺次连接四边形A1B1C1D1的中点,得到四边形A2B2C2D2,在顺次连接四边形A2B2C2D2四边的中点,得到四边形A3B3C3D3,…,按此方法得到的四边形A8B8C8D8的周长为.
三、解答题(共72分)
17.(6分)如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,AC=12
cm,BC=16
cm,求AD,CD的长.
解:∵∠ACB=90°,AC=12
cm,BC=16
cm,
∴AB=20
cm.
根据直角三角形的面积公式,得CD==9.6
cm.
在Rt△ACD中,AD==7.2
cm.
18.(6分)如图,在四边形ABCD中,E,F,G,H分别是AD,BD,BC,AC上的中点,AB=5,CD=7.求四边形EFGH的周长.
解:∵E,F,G,H分别是AD,BD,BC,AC上的中点,AB=5,CD=7.
∴EF∥AB∥GH,EH∥CD∥FG,EF=2.5,EH=3.5.
∴四边形EFGH为平行四边形.
∴四边形EFGH的周长为2(EF+EH)=2×6=12.
19.(8分)(益阳中考)如图,在 ABCD中,AE⊥BD于点E,CF⊥BD于点F,连接AF,CE.求证:AF=CE.
证明:∵四边形ABCD是平行四边形,
∴AD=BC,∠ADB=∠CBD.
又∵AE⊥BD,CF⊥BD,
∴∠AED=∠CFB,AE∥CF.
∴△AED≌△CFB(AAS).
∴AE=CF.
∴四边形AECF是平行四边形.
∴AF=CE.
20.(10分)如图,点P是∠MON中一点,PA⊥OM于点A,PB⊥ON于点B,连接AB,∠PAB=∠PBA.
(1)求证:OP平分∠MON;
(2)若∠MON=80°,求∠PAB的度数.
解:(1)证明:∵∠PAB=∠PBA,
∴PA=PB.
∵PA⊥OM,PB⊥ON,
∴OP平分∠MON.
(2)∵∠MON=80°,PA⊥OM,PB⊥ON,
∴∠APB=360°-90°×2-80°=100°.
∵∠PAB=∠PBA,
∴∠PAB=×(180°-100°)=40°.
21.(10分)(眉山中考)如图,在方格网中已知格点△ABC和点O.
(1)画△A′B′C′和△ABC关于点O成中心对称;
(2)请在方格网中标出所有使以点A,O,C′,D为顶点的四边形是平行四边形的D点.
解:(1)如图所示.
(2)根据题意画图如下:
22.(10分)(雅安中考)如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE.连接DE.
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.
解:(1)证明:∵△BAD是由△BEC绕点B旋转60°而得,
∴DB=CB,∠ABD=∠EBC,∠ABE=60°.
又∵AB⊥BC,∴∠ABC=90°.∴∠DBE=∠CBE=30°.
在△BDE和△BCE中,∴△BDE≌△BCE(SAS).
(2)四边形ABED是菱形.理由:由(1)得△BDE≌△BCE.
又∵△BAD是由△BEC旋转得到,∴△BAD≌△BEC.
∴BA=BE,AD=ED=EC.又∵BE=CE,∴AB=BE=ED=DA.
∴四边形ABED是菱形.
23.(10分)如图,P是正方形ABCD对角线AC上一点,点E在BC上,且PE=PB.
(1)求证:PE=PD;
(2)连接DE,试求∠PED的度数.
解:(1)证明:∵四边形ABCD是正方形,
∴BC=CD,∠ACB=∠ACD,
在△PBC和△PDC中,
∴△PBC≌△PDC(SAS).
∴PB=PD.
∵PE=PB.
∴PE=PD.
(2)∵四边形ABCD是正方形,
∴∠BCD=90°.
∵△PBC≌△PDC,
∴∠PBC=∠PDC.
∵PE=PB,
∴∠PBC=∠PEB.
∴∠PDC=∠PEB.
∵∠PEB+∠PEC=180°,
∴∠PDC+∠PEC=180°.
在四边形PECD中,∠EPD=360°-
(∠PDC+∠PEC)-∠BCD=360°-180°-90°=90°,
又∵PE=PD,
∴△PDE是等腰直角三角形.
∴∠PED=45°.
24.(12分)(兰州中考)给出定义,若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称该四边形为勾股四边形.
(1)在你学过的特殊四边形中,写出两种勾股四边形的名称;
(2)如图,将△ABC绕顶点B按顺时针方向旋转60°得到△DBE,连接AD,DC,CE,已知:∠DCB=30°.
①求证:△BCE是等边三角形;
②求证:DC2+BC2=AC2,即四边形ABCD是勾股四边形.
解:(1)正方形、矩形.
(2)证明:①由旋转的性质得△ABC≌△DBE,
∴BC=BE.
∵∠CBE=60°,∴△BCE是等边三角形.
②∵△ABC≌△DBE,
∴BE=BC,AC=DE.
∵△BCE为等边三角形,
∴BC=CE,∠BCE=60°.
∵∠DCB=30°,∴∠DCE=90°.
在Rt△DCE中,DC2+CE2=DE2,
∴DC2+BC2=AC2.
同课章节目录
