浙江省温州市重点高中2016年保送生文化水平测试九年级数学试卷及答案
文档属性
| 名称 | 浙江省温州市重点高中2016年保送生文化水平测试九年级数学试卷及答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 466.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-11 00:00:00 | ||
图片预览



文档简介
温州市重点高中2016年保送生文化水平测试九年级数学试卷
2016.1
(本卷满分:150分
考试时间:100分钟)
注:不得使用计算器及其他任何电子产品
一、单项选择题(本大题分5小题,每题4分,共20分)
若可以写成个连续的正整数之和,则的最大值为············(
)
A、65
B、64
C、54
D、27
已知中,BC=a,AC=b,AB=c,且2b=a+c,延长CA到D,使AD=AB
连结BD,则的值为·······················(
)
A、
B、
C、
D、
方程组的有理数解的个数为·············(
)
A、1
B、2
C、3
D、4
有n个人,已知他们中的任意两人至多通电话
( http: / / www.21cnjy.com )一次,他们中的任意n-2个人之间通电话的次数相等,都是3k次,其中k是自然数,则n的所有可能值有(
)
A、1个
B、2个
C、3个
D、4个
如图,正方形ABCD内接于⊙O,P为劣弧上一点,PA交BD于点M,PB交AC于点N,记∠PAC=θ,若MN⊥PA,则2-的值为········(
)
A、1
B、
C、
D、
二、简答题(本大题分10小题,每空5分,共50分)
北京市实行汽车限行,每一辆车周一到周五工作
( http: / / www.21cnjy.com )日5天内限行一天,某公司因工作需要,周一到周四要用9辆车,周五要用11辆车,如果公司能够自行选择车辆的停驶日期,那么该公司至少应有
辆车.
在9×9的方格表中,共有81个小方格.在每
( http: / / www.21cnjy.com )一个小方格中,写上一个数.如果只要每行、每列至多有三个不同的数,就能保证在方格表中存在一个数,这个数在某一行中至少出现n次,在某一列中也至少出现n次,那么,n的最大值是
.
设等边的内切圆半径为2,圆心为.若点满足,则与的面积之比的最大值为
.
对一个5×n的方格阵用红蓝
( http: / / www.21cnjy.com )两色进行染色.如果对任意一种染色方案,总可以找到由3行及3列相交所得到的同色9个方格,则n的最小值为
.
抛物线族(m是参数)与为圆心、1为半径的圆内部相交部分的面积为
.
某市发出车牌号码均由6个数字(从0到9
( http: / / www.21cnjy.com ))组成,该市规定:任意2个车牌至少要有2对同一某市发出车牌号码均由6个数字(从0到9)组成,该市规定:任意2个车牌至少要有2对同一数位上的数字不同(如车牌号038471和030471不能同时使用).则该市最多能发出
个不同车牌.
在锐角三角形ABC中,AB上的高C
( http: / / www.21cnjy.com )E与AC上的高BD相交于点H,以DE为直径的圆分别交AB、AC于F、G两点,FG与AH相交于点K,已知BC=25,BD=20,BE=7,则AK的长为
.
从1,2,…,2008中选出总和为
( http: / / www.21cnjy.com )1009000的1004个数,并且这1004个数中的任意两数之和都不等于2009.则这1004个数的平方和等于
.
在平面直角坐标系中,点O为坐标原点,点A,B,C,P的坐标分别为(6,0),(6,3),(,),(4,2),过点P的直线l与四边形OABC一组对边相交,将四边形OABC分为两个四边形,则其中以点O为顶点的四边形的面积的最大值为
.
三个半径为r的圆能覆盖边长为16的正方形,则r的最小值为
.
三、分析解答题(本大题分6小题,分值依次为15分、15分、15分、15分、20分、20分,20、21题选做一题,共80分)
(15分)如图,在四边形ABCD中,对角线A
( http: / / www.21cnjy.com )C平分∠BAD.在CD上取一点E,BE与AC相交于F,延长DF交BC于G.求证:∠GAC=∠EAC.
[证明]
(15分)设是十进制中的素数,证明:b2-4ac不是完全平方数.
[证明]
(15分)试求出所有满足下
( http: / / www.21cnjy.com )列条件的正整数a,b,c,d,其中1(15分)已知有限张卡片
( http: / / www.21cnjy.com ),每张卡片上各写有一个小于30的正数,所有卡片上数的和为1080.现将这些卡片按下列要求一批一批地取走(不放回)直至取完.首先从这些卡片中取出第一批卡片,其数字之和为S1,满足S1≤120,且S1要尽可能地大;然后在取出第一批卡片后,对余下的卡片按第一批的取卡要求构成第二批卡片(其数字之和为S2);如此继续构成第三批(其数字之和为S3);第四批(其数字之和为S4);…直到第N批(其数字之和为SN)取完所有卡片为止.
(1)
判断S1,S2,…,SN的大小关系,并指出除第N批外,每批至少取走的卡片数为多少?
(2)
当n=1,2,3,…,N-2时,求证:;
(3)
对于任意满足条件的有限张卡片,证明:N≤11.
[注意]
20、21题选做一题,如有时间空余两题均正确者,得分乘80%计入总分
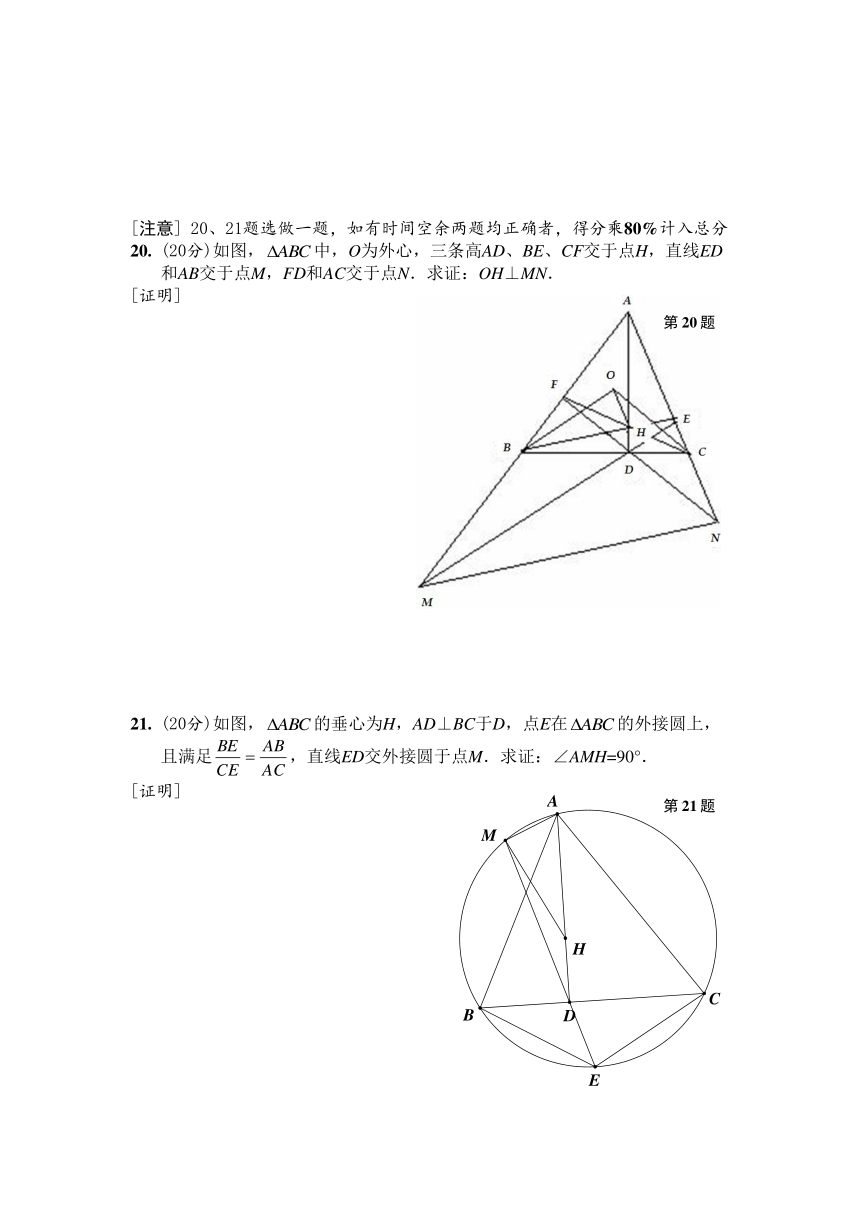
(20分)如图,中,O为外心,三条高AD、BE、CF交于点H,直线ED和AB交于点M,FD和AC交于点N.求证:OH⊥MN.
[证明]
(20分)如图,的垂心为H,AD⊥BC于D,点E在的外接圆上,且满足,直线ED交外接圆于点M.求证:∠AMH=90°.
[证明]
2016年重高保送生文化水平测试
数学试卷
参
考
答
案
及
评
分
建
议
[改卷须知]
本卷20、21题选做一题,如有时间空余两题均正确者,得分乘80%计入总分
一、单项选择题(本大题分5小题,每题4分,共20分)
[
1~5
]
C
B
B
B
A
二、简答题(本大题分10小题,每空5分,共50分)
[本大题评分建议:若数字书写不清晰,不给分]
6、
12
7、
3
8、
9、
41
10、
11、
105
12、
13、
1351373940
14、
10
15、
三、分析解答题(本大题分6小题,分值依次为15分、15分、15分、15分、20分、20分,共80分)
16、(10分)(4分+2分+2分+2分=10分)
【证明】连结BD交AC于H.对BCD用塞瓦定理,可得
因为AH是∠BAD的平分线,由角平分线定理,可得.(4分)
故.(2分)
过点C作AB的平行线AG的延长线于I,过点C作AD的平行线交AE的延长线于J.
则,.所以,
从而,CI=CJ.(2分)
又因为
CI∥AB,CJ∥AD,
故∠ACI=π-∠ABC=π-∠DAC=∠ACJ.
因此,ACI≌ACJ.(2分)
从而,∠IAC=∠JAC,即
∠GAC=∠EAC
17、(10分)(可能有多种解法)
( http: / / www.21cnjy.com )
18、(15分)(解法可能有多种)【解】
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
19、(3+5+7=15分)
【解答】(1)解:对于任意满足条件的有
( http: / / www.21cnjy.com )限张卡片,满足S1≥S2≥…≥SN;假设每批取出卡片不多于3张,则这3张卡片上的数之和不大于90,而剩下的每个数不大于30,由已知条件知,应该选4张,与假设矛盾,除第N批外,每批至少取走的卡片数为4张.
(2)证明:当取出第n批后,因为n=1,2,3,…,N-2,此时第n+1批卡片还没取完,此时余下的每个数必大于120-Sn+1,余下数之和更大于120-Sn+1,即1080-(S1+S2+…+Sn+1)>120-Sn+1,由此可得S1+S2+…+Sn<960,因为nSn≤S1+S2+…+Sn,从而;
(3)证明:假设N>11,即第11批卡片取走后,还有卡片没被分完,由已知可知余下的每个数都大于120-S11,且120-S11≥120-S10,故余下的每个数>120-S11≥120-S10>120-=24,因为第11组卡片中至少含有4张,所以第11组卡片上的所有数之和S11大于24×4=96,从而S10≥S11>96,这与(2)中的S10<96矛盾,所以N≤11.
20、(20分)(解法可能有多种,细致
( http: / / www.21cnjy.com )找分点,给分分为5档:0分、5分、10分、15分、20分,注:学生可能用“易证”、“可证”等词骗取分数,此题需慢改)
【证明】(1)∵A、C、D、F四点共圆
∴∠BDF=∠BAC
又∠OBC=(180°-∠BOC)=90°-∠BAC
∴OB⊥DF.
(2)∵CF⊥MA∴MC
2-MH
2=AC
2-AH
2(①)
∵BE⊥NA∴NB
2-NH
2=AB
2-AH
2
(②)
∵DA⊥BC∴BD
2-CD
2=BA
2-AC
2
(③)
∵OB⊥DF∴BN
2-BD
2=ON
2-OD
2
(④)
∵OC⊥DE∴CM
2-CD
2=OM
2-OD
2(⑤)………………………………15分
①-②+③+④-⑤,得NH
2-MH
2=ON
2-OM
2
MO
2-MH
2=NO
2-NH
2
∴OH⊥MN………………………………………………………………20分
【另证】以BC所在直线为x轴,D为原点建立直角坐标系,设A(0,a),B(b,0),C(c,0),则
∴直线AC的方程为,直线BE的方程为由
,得E点坐标为E(),
同理可得F(),直线AC的垂直平分线方程为,直线BC的垂直平分线方程为,由
得O(),
,
∵,∴OB⊥DF.同理可证OC⊥DE.在直线BE的方程中令x=0得H(0,).∴,直线DF的方程为,由,得N
().同理可得M
(),∴,∵kOH
·kMN
=-1,∴OH⊥MN.
21、(20分)(解法可能有多种,
( http: / / www.21cnjy.com )细致找分点,给分分为5档:0分、5分、10分、15分、20分,注:学生可能用“易证”、“可证”等词骗取分数,此题需慢改)
【证明】作高BP、CQ.连结MB、MC、MP、MQ、PQ.一方面,,另一方面,由Ceva定理(塞瓦定理):,由①、②,,又∠MBA=∠MCA.得,于是M、A、P、Q四点共圆,即M、A、P、Q、H五点共圆,而AH为直径,∴∠AMH=90°.
【另证】取BC中点G,连结AG、EG、GC、BH、CI、BI(作点令,连结交⊙O于I),有,四边形BHCI为平行四边形,A、、D、G四点共圆
第5题
第12题
第16题
第20题
第21题
第16题解
2016.1
(本卷满分:150分
考试时间:100分钟)
注:不得使用计算器及其他任何电子产品
一、单项选择题(本大题分5小题,每题4分,共20分)
若可以写成个连续的正整数之和,则的最大值为············(
)
A、65
B、64
C、54
D、27
已知中,BC=a,AC=b,AB=c,且2b=a+c,延长CA到D,使AD=AB
连结BD,则的值为·······················(
)
A、
B、
C、
D、
方程组的有理数解的个数为·············(
)
A、1
B、2
C、3
D、4
有n个人,已知他们中的任意两人至多通电话
( http: / / www.21cnjy.com )一次,他们中的任意n-2个人之间通电话的次数相等,都是3k次,其中k是自然数,则n的所有可能值有(
)
A、1个
B、2个
C、3个
D、4个
如图,正方形ABCD内接于⊙O,P为劣弧上一点,PA交BD于点M,PB交AC于点N,记∠PAC=θ,若MN⊥PA,则2-的值为········(
)
A、1
B、
C、
D、
二、简答题(本大题分10小题,每空5分,共50分)
北京市实行汽车限行,每一辆车周一到周五工作
( http: / / www.21cnjy.com )日5天内限行一天,某公司因工作需要,周一到周四要用9辆车,周五要用11辆车,如果公司能够自行选择车辆的停驶日期,那么该公司至少应有
辆车.
在9×9的方格表中,共有81个小方格.在每
( http: / / www.21cnjy.com )一个小方格中,写上一个数.如果只要每行、每列至多有三个不同的数,就能保证在方格表中存在一个数,这个数在某一行中至少出现n次,在某一列中也至少出现n次,那么,n的最大值是
.
设等边的内切圆半径为2,圆心为.若点满足,则与的面积之比的最大值为
.
对一个5×n的方格阵用红蓝
( http: / / www.21cnjy.com )两色进行染色.如果对任意一种染色方案,总可以找到由3行及3列相交所得到的同色9个方格,则n的最小值为
.
抛物线族(m是参数)与为圆心、1为半径的圆内部相交部分的面积为
.
某市发出车牌号码均由6个数字(从0到9
( http: / / www.21cnjy.com ))组成,该市规定:任意2个车牌至少要有2对同一某市发出车牌号码均由6个数字(从0到9)组成,该市规定:任意2个车牌至少要有2对同一数位上的数字不同(如车牌号038471和030471不能同时使用).则该市最多能发出
个不同车牌.
在锐角三角形ABC中,AB上的高C
( http: / / www.21cnjy.com )E与AC上的高BD相交于点H,以DE为直径的圆分别交AB、AC于F、G两点,FG与AH相交于点K,已知BC=25,BD=20,BE=7,则AK的长为
.
从1,2,…,2008中选出总和为
( http: / / www.21cnjy.com )1009000的1004个数,并且这1004个数中的任意两数之和都不等于2009.则这1004个数的平方和等于
.
在平面直角坐标系中,点O为坐标原点,点A,B,C,P的坐标分别为(6,0),(6,3),(,),(4,2),过点P的直线l与四边形OABC一组对边相交,将四边形OABC分为两个四边形,则其中以点O为顶点的四边形的面积的最大值为
.
三个半径为r的圆能覆盖边长为16的正方形,则r的最小值为
.
三、分析解答题(本大题分6小题,分值依次为15分、15分、15分、15分、20分、20分,20、21题选做一题,共80分)
(15分)如图,在四边形ABCD中,对角线A
( http: / / www.21cnjy.com )C平分∠BAD.在CD上取一点E,BE与AC相交于F,延长DF交BC于G.求证:∠GAC=∠EAC.
[证明]
(15分)设是十进制中的素数,证明:b2-4ac不是完全平方数.
[证明]
(15分)试求出所有满足下
( http: / / www.21cnjy.com )列条件的正整数a,b,c,d,其中1
( http: / / www.21cnjy.com ),每张卡片上各写有一个小于30的正数,所有卡片上数的和为1080.现将这些卡片按下列要求一批一批地取走(不放回)直至取完.首先从这些卡片中取出第一批卡片,其数字之和为S1,满足S1≤120,且S1要尽可能地大;然后在取出第一批卡片后,对余下的卡片按第一批的取卡要求构成第二批卡片(其数字之和为S2);如此继续构成第三批(其数字之和为S3);第四批(其数字之和为S4);…直到第N批(其数字之和为SN)取完所有卡片为止.
(1)
判断S1,S2,…,SN的大小关系,并指出除第N批外,每批至少取走的卡片数为多少?
(2)
当n=1,2,3,…,N-2时,求证:;
(3)
对于任意满足条件的有限张卡片,证明:N≤11.
[注意]
20、21题选做一题,如有时间空余两题均正确者,得分乘80%计入总分
(20分)如图,中,O为外心,三条高AD、BE、CF交于点H,直线ED和AB交于点M,FD和AC交于点N.求证:OH⊥MN.
[证明]
(20分)如图,的垂心为H,AD⊥BC于D,点E在的外接圆上,且满足,直线ED交外接圆于点M.求证:∠AMH=90°.
[证明]
2016年重高保送生文化水平测试
数学试卷
参
考
答
案
及
评
分
建
议
[改卷须知]
本卷20、21题选做一题,如有时间空余两题均正确者,得分乘80%计入总分
一、单项选择题(本大题分5小题,每题4分,共20分)
[
1~5
]
C
B
B
B
A
二、简答题(本大题分10小题,每空5分,共50分)
[本大题评分建议:若数字书写不清晰,不给分]
6、
12
7、
3
8、
9、
41
10、
11、
105
12、
13、
1351373940
14、
10
15、
三、分析解答题(本大题分6小题,分值依次为15分、15分、15分、15分、20分、20分,共80分)
16、(10分)(4分+2分+2分+2分=10分)
【证明】连结BD交AC于H.对BCD用塞瓦定理,可得
因为AH是∠BAD的平分线,由角平分线定理,可得.(4分)
故.(2分)
过点C作AB的平行线AG的延长线于I,过点C作AD的平行线交AE的延长线于J.
则,.所以,
从而,CI=CJ.(2分)
又因为
CI∥AB,CJ∥AD,
故∠ACI=π-∠ABC=π-∠DAC=∠ACJ.
因此,ACI≌ACJ.(2分)
从而,∠IAC=∠JAC,即
∠GAC=∠EAC
17、(10分)(可能有多种解法)
( http: / / www.21cnjy.com )
18、(15分)(解法可能有多种)【解】
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
19、(3+5+7=15分)
【解答】(1)解:对于任意满足条件的有
( http: / / www.21cnjy.com )限张卡片,满足S1≥S2≥…≥SN;假设每批取出卡片不多于3张,则这3张卡片上的数之和不大于90,而剩下的每个数不大于30,由已知条件知,应该选4张,与假设矛盾,除第N批外,每批至少取走的卡片数为4张.
(2)证明:当取出第n批后,因为n=1,2,3,…,N-2,此时第n+1批卡片还没取完,此时余下的每个数必大于120-Sn+1,余下数之和更大于120-Sn+1,即1080-(S1+S2+…+Sn+1)>120-Sn+1,由此可得S1+S2+…+Sn<960,因为nSn≤S1+S2+…+Sn,从而;
(3)证明:假设N>11,即第11批卡片取走后,还有卡片没被分完,由已知可知余下的每个数都大于120-S11,且120-S11≥120-S10,故余下的每个数>120-S11≥120-S10>120-=24,因为第11组卡片中至少含有4张,所以第11组卡片上的所有数之和S11大于24×4=96,从而S10≥S11>96,这与(2)中的S10<96矛盾,所以N≤11.
20、(20分)(解法可能有多种,细致
( http: / / www.21cnjy.com )找分点,给分分为5档:0分、5分、10分、15分、20分,注:学生可能用“易证”、“可证”等词骗取分数,此题需慢改)
【证明】(1)∵A、C、D、F四点共圆
∴∠BDF=∠BAC
又∠OBC=(180°-∠BOC)=90°-∠BAC
∴OB⊥DF.
(2)∵CF⊥MA∴MC
2-MH
2=AC
2-AH
2(①)
∵BE⊥NA∴NB
2-NH
2=AB
2-AH
2
(②)
∵DA⊥BC∴BD
2-CD
2=BA
2-AC
2
(③)
∵OB⊥DF∴BN
2-BD
2=ON
2-OD
2
(④)
∵OC⊥DE∴CM
2-CD
2=OM
2-OD
2(⑤)………………………………15分
①-②+③+④-⑤,得NH
2-MH
2=ON
2-OM
2
MO
2-MH
2=NO
2-NH
2
∴OH⊥MN………………………………………………………………20分
【另证】以BC所在直线为x轴,D为原点建立直角坐标系,设A(0,a),B(b,0),C(c,0),则
∴直线AC的方程为,直线BE的方程为由
,得E点坐标为E(),
同理可得F(),直线AC的垂直平分线方程为,直线BC的垂直平分线方程为,由
得O(),
,
∵,∴OB⊥DF.同理可证OC⊥DE.在直线BE的方程中令x=0得H(0,).∴,直线DF的方程为,由,得N
().同理可得M
(),∴,∵kOH
·kMN
=-1,∴OH⊥MN.
21、(20分)(解法可能有多种,
( http: / / www.21cnjy.com )细致找分点,给分分为5档:0分、5分、10分、15分、20分,注:学生可能用“易证”、“可证”等词骗取分数,此题需慢改)
【证明】作高BP、CQ.连结MB、MC、MP、MQ、PQ.一方面,,另一方面,由Ceva定理(塞瓦定理):,由①、②,,又∠MBA=∠MCA.得,于是M、A、P、Q四点共圆,即M、A、P、Q、H五点共圆,而AH为直径,∴∠AMH=90°.
【另证】取BC中点G,连结AG、EG、GC、BH、CI、BI(作点令,连结交⊙O于I),有,四边形BHCI为平行四边形,A、、D、G四点共圆
第5题
第12题
第16题
第20题
第21题
第16题解
同课章节目录
