七年级数学下册5.2.2平行线的判定课件
文档属性
| 名称 | 七年级数学下册5.2.2平行线的判定课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 724.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-12 00:00:00 | ||
图片预览









文档简介
课件40张PPT。第五章 相交线与平行线5.2.2 平行线的判定?教学新知方法1:平行线的定义。
方法2:两条直线都与第三条直线平行,那么这两条直线也平行。
方法3:同位角相等,两直线平行。
方法4:内错角角相等,两直线平行。
方法5:同旁内角互补,两直线平行。知识要点2.会用平行线的判定方法判定两直线平行,初步学会用几何语言进行简单推理和表述。1.从“用三角尺和直尺画平行线的活动过程中发现”同位角相等,两直线平行;培养学生动手操作,主动探究及合作交流的能力。知识梳理知识点1:平行线的画法.画平行线的口诀:一放、二靠、三移、四画.【例】如图5-2-20,过A点画出底边的平行线.知识梳理【讲解】把三角板的一条直角边与已知直线重合,用直尺靠紧三角板的另一条直角边,沿直尺移动三角板,使三角板的原来和已知直线重合的直角边和A点重合,过A点沿三角板的直角边画直线即可.画图如图5-2-21所示.知识梳理【方法小结】利用直尺和三角板画过直线外一点的已知直线的平行线,是几何画图的基本技能之一.一放:把三角板一边落在已知直线上;二靠:用直尺紧靠三角板的另一边;三移:沿直尺移动三角板,使三角板与已知直线重合的边过已知点;四画:沿三角板过已知点的边画直线.【小练习】
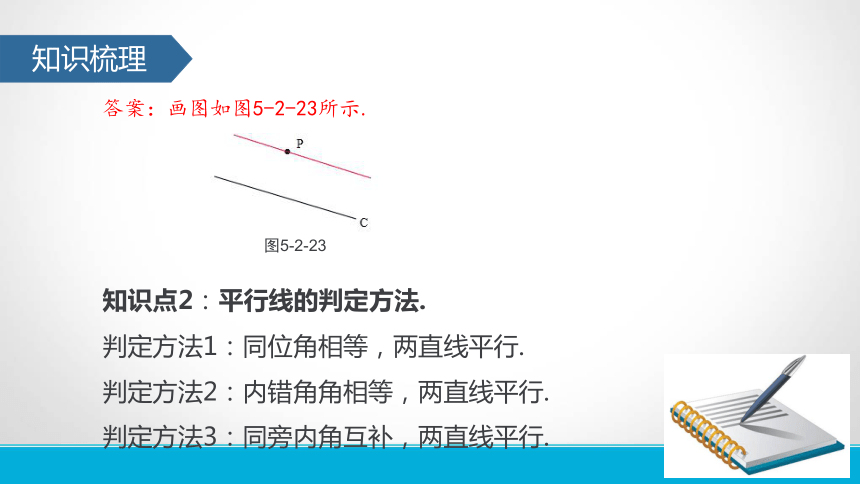
如图5-2-22,过P点画直线c的平行线.知识梳理答案:画图如图5-2-23所示.知识点2:平行线的判定方法.判定方法1:同位角相等,两直线平行.
判定方法2:内错角角相等,两直线平行.
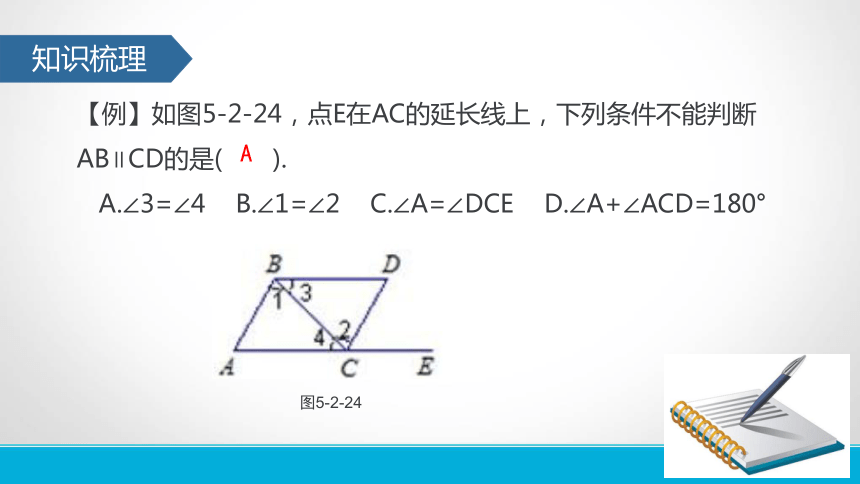
判定方法3:同旁内角互补,两直线平行.知识梳理【例】如图5-2-24,点E在AC的延长线上,下列条件不能判断AB∥CD的是( ).
A.∠3=∠4 B.∠1=∠2 C.∠A=∠DCE D.∠A+∠ACD=180°A知识梳理【讲解】根据图形可知,∠3与∠4是BD与AE被BC所截得到的内错角,由∠3=∠4可以得到BD∥AE;∠1与∠2是AB与CD被BC所截得到的内错角,由∠1=∠2可以得到AB∥CD;∠A=∠DCE是AB与CD被AE所截得到的同位角,由∠A=∠DCE可以得到AB∥CD;∠A与∠ACD是AB与CD被AE所截得到的同旁内角,由∠A+∠ACD=180°可以得到AB∥CD,所以本题的答案应选择A.【方法小结】准确地识别三种角是判断哪两条直线平行的前提条件,一般地“F”形中有同位角,“N”形中有内错角,“U”形中有同旁内角.每一对角的公共边所在的直线是截线,另外两边所在的直线是被截线,即判断平行的两条直线.知识梳理【小练习】
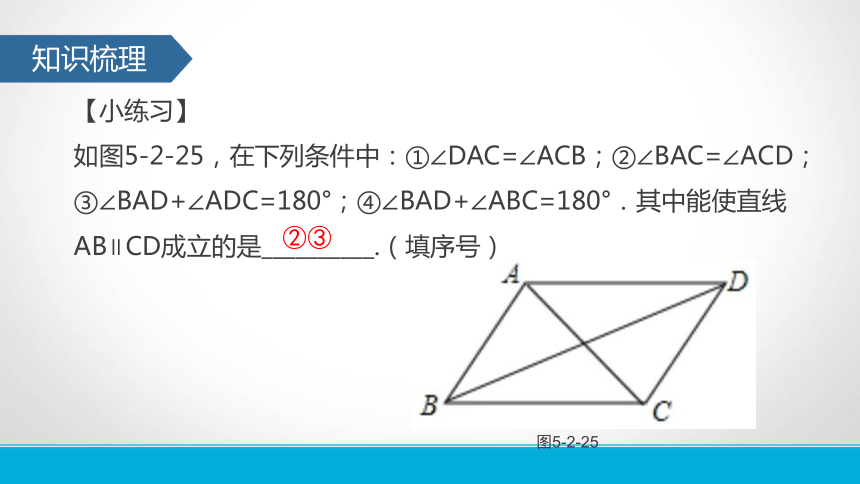
如图5-2-25,在下列条件中:①∠DAC=∠ACB;②∠BAC=∠ACD;③∠BAD+∠ADC=180°;④∠BAD+∠ABC=180°.其中能使直线AB∥CD成立的是__________.(填序号) ②③知识梳理2.如图5-2-26,根据下列条件,可以判定哪两条直线平行?并说明判定的根据是什么.
①∠2=∠B;②∠1=∠D;③∠3+∠F=180°.知识梳理答案:解:①∠2=∠B,可判断AB∥ED,根据“同位角相等,两直线平行”;②∠1=∠D,可判断AC∥FD,根据“内错角相等,两直线平行”;③∠3+∠F=180°,可判断AC∥FD,根据“同旁内角互补,两直线平行”.中考在线
考点:平行线的判定【例1】(2015?黔南州)如图5-2-27,下列说法错误的是( ).
A.若a∥b,b∥c,则a∥c B.若∠1=∠2,则a∥c
C.若∠3=∠2,则b∥c D.若∠3+∠5=180°,则a∥cC知识梳理【解析】根据平行线的判定进行判断:A.若a∥b,b∥c,则a∥c,利用了平行公理,正确;B.若∠1=∠2,则a∥c,利用了内错角相等,两直线平行,正确;C.∠3=∠2,不能判断b∥c,错误;D.若∠3+∠5=180°,则a∥c,利用同旁内角互补,两直线平行,正确;故选C.知识梳理【方法小结】此题考查平行线的判定,关键是根据几种平行线判定的方法进行分析.实战演练
1.(2015?福州)下列图形中,由∠1=∠2能得到AB∥CD的是( ).B知识梳理2.(2014?汕尾)如图5-2-28,能判定EB∥AC的条件是( ).
A.∠C=∠ABE B.∠A=∠EBD C.∠C=∠ABC D.∠A=∠ABED知识梳理3.(2014?湘潭)如图5-2-29,直线a、b被直线c所截,若满足________________________________________,则a、b平行. ∠1=∠2或∠2=∠3或∠3+∠4=180°知识梳理4.(2014?汕尾)已知a,b,c为平面内三条不同直线,若a⊥b,c⊥b,则a与c的位置关系是_______________. 平行课堂练习1.如图5-2-35,己知∠1=145°,∠2=145°,则AB∥CD,依据是___________________________.同位角相等,两直线平行课堂练习2.如图5-2-36 是一条街道的两个拐角,∠ABC与∠BCD均为140°,则街道AB与CD的关系是_________,这是因___________________. 答案:平行;内错角相等,两直线平行。课堂练习3.如图5-2-37一个弯形管道ABCD的拐角∠ABC=120°,∠BCD
=60°,这时说管道AB∥CD,是根据_________________________. 同旁内角互补,两直线平行课堂练习4.如图5-2-38:(1)由∠A=∠3可以判断_____∥_____,根据是____________________________;
(2)由∠2=∠E可以判断_____∥_____,根据是_________________
_______________;
(3)由∠C+∠DBC=180°可以判断______∥______,根据是_____
______________________________.图5-2-38BEAD同位角相等,两直线平行CEBDCEBD内错角相等,两直线平行同旁内角互补,两直线平行答案:(1)AD,BE,同位角相等,两直线平行;(2)BD,CE,内错角相等,两直线平行;(3)BD,CE,同旁内角互补,两直线平行.课堂练习5.如图5-2-39,请完成下列各题:
(1)如果∠1=______,那么DE∥AC(_______________________);
(2)如果∠1=______,那么EF∥BC(_______________________);∠C同位角相等,两直线平行内错角相等,两直线平行∠FED课堂练习(3)如果∠FED+_______=180°,那么AC∥ED(______________
______________);
(4)如果∠2+__________=180°,那么AB∥DF(______________
_______________).∠EFC∠AED同旁内角互补,两直线平行同旁内角互补,两直线平行课堂练习讲评:本题考查的是平行线的判定,根据平行线的判定定理对各选项进行逐一分析即可.6.如图5-2-40,已知:AB∥CD,∠1=∠2,则AB与EF有怎样的位置关系?为什么?课堂练习答案:AB∥EF.因为∠1=∠2,所以CD∥EF,又因为AB∥CD,所以AB∥EF(平行于同一条直线的两条直线互相平行).讲评:本题考查平行线判定方法的灵活使用,以及探究、推理能力.先根据∠1=∠2,得出CD∥EF,再根据AB∥CD,利用平行公理推论解答.7.已知:如图5-2-41,∠BCD=∠B+∠D,试说明AB∥ED.课堂练习答案:如图5-2-42,过点C作∠BCF=∠B,∴AB∥CF.∵∠BCD=∠B+∠D,∠BCD=∠BCF+∠DCF,∴∠DCF=∠D,∴ED∥CF,∴AB∥ED(平行于同一条直线的两条直线互相平行).讲评:本题考查平行线判定方法的应用.解答时,需要添加辅助线,构造角的关系来完成说明.8.如图5-2-43,AB⊥BD,CD⊥MN,垂足分别是B、D点,∠FDC
=∠EBA.
(1)判断CD与AB的位置关系;(2)BE与DF平行吗?为什么?课堂练习答案:(1)CD∥AB,理由是:∵AB⊥BD,∴∠ABD=90°,同理∠CDM=90°,∴∠ABD=∠CDM,∴CD∥AB(同位角相等,两直线平行).
(2)BE∥DF,理由是:∵∠ABD=∠CDM=90°,∠FDC=∠EBA,∴∠ABD-∠EBA=∠CDM-∠FDC,∴∠EBM=∠FDM,∴BE∥DF(同位角相等,两直线平行).课堂练习讲评:解答此类要判定两直线平行的题,可围绕截线找同位角、内错角和同旁内角.(1)利用垂直得一对同位角相等来判断两条直线平行;(2)利用等角的余角相等,得出一对同位角相等来判定两直线平行.课后习题1.如图5-2-44,给出了过直线外一点作已知直线的平行线的方法,其依据是( ).
A.两直线平行,同位角相等 B.内错角相等,两直线平行
C.同旁内角互补,两直线平行 D.同位角相等,两直线平行D课后习题2.用两块相同的三角板按如图5-2-45所示的方式作平行线AB和CD,能解释其中的道理的依据是( )
A.内错角相等,两直线平行 B.同位角相等,两直线平行
C.同旁内角互补,两直线平行 D.平等于同一直线的两直线平行A课后习题3.如图5-2-46,直线a,b都与直线c相交,给出的下列条件:①∠1=∠7;②∠3=∠5;③∠1+∠8=180°;④∠3=∠6.其中能判断a∥b的是( ).
A.①③ B.②③ C.③④ D.①②③D课后习题4.如图5-2-47,下面推理中,正确的是( ).
A.∵∠A+∠D=180°,∴AD∥BC B.∵∠C+∠D=180°,∴AB∥CD
C.∵∠A+∠D=180°,∴AB∥CD D.∵∠A+∠C=180°,∴AB∥CDC课后习题5.如图5-2-48所示,点E在AC的延长线上,下列条件中能判断AB∥CD的是( ).
A.∠3=∠4 B.∠1=∠2 C.∠D=∠DCE
D.∠D+∠ACD=180°B课后习题6.已知:如图5-2-49,∠EAD=∠DCF,要得到AB∥CD,则需要的条件______________.(填一个你认为正确的条件即可)∠EAD=∠B课后习题7.如图5-2-50,BC平分∠DBA,∠1=∠2,填空:因为BC平分∠DBA,所以∠1=_________,所以∠2=___________,所以AB∥
_______.∠CBA∠CBACD课后习题8.已知:如图5-2-51,AB⊥BC,BC⊥CD且∠1=∠2,求证:BE∥CF.答案:证明:∵AB⊥BC,BC⊥CD,∴∠ABC=∠DCB=90°,∵∠1=∠2,∴∠ABC-∠1=∠DCB-∠2,∴∠CBE=∠BCF,∴BE∥CF.课后习题9.如图5-2-52,已知∠1=50°,∠2=65°,CD平分∠ECF,则CD∥FG.请说明理由.课后习题?10.将一副直角三角尺拼成如图5-2-53所示的图形,过点C作CF平分∠DCE交DE于点F,试判断CF与AB是否平行,并说明理由.?课后习题11.如图5-2-54所示,要想判断AB是否与CD平行,我们可以测量哪些角;请你写出三种方案,并说明理由.课后习题答案:解:(1)可以测量∠EAB与∠D,如果∠EAB=∠D,那么根据同位角相等,两直线平行,得出AB与CD平行.(2)可以测量∠BAC与∠C,如果∠BAC=∠C,那么根据内错角相等,两直线平行,得出AB与CD平行.(3)可以测量∠BAD与∠D,如果∠BAD+∠D=180°,那么根据同旁内角互补,两直线平行,得出AB与CD平行.
方法2:两条直线都与第三条直线平行,那么这两条直线也平行。
方法3:同位角相等,两直线平行。
方法4:内错角角相等,两直线平行。
方法5:同旁内角互补,两直线平行。知识要点2.会用平行线的判定方法判定两直线平行,初步学会用几何语言进行简单推理和表述。1.从“用三角尺和直尺画平行线的活动过程中发现”同位角相等,两直线平行;培养学生动手操作,主动探究及合作交流的能力。知识梳理知识点1:平行线的画法.画平行线的口诀:一放、二靠、三移、四画.【例】如图5-2-20,过A点画出底边的平行线.知识梳理【讲解】把三角板的一条直角边与已知直线重合,用直尺靠紧三角板的另一条直角边,沿直尺移动三角板,使三角板的原来和已知直线重合的直角边和A点重合,过A点沿三角板的直角边画直线即可.画图如图5-2-21所示.知识梳理【方法小结】利用直尺和三角板画过直线外一点的已知直线的平行线,是几何画图的基本技能之一.一放:把三角板一边落在已知直线上;二靠:用直尺紧靠三角板的另一边;三移:沿直尺移动三角板,使三角板与已知直线重合的边过已知点;四画:沿三角板过已知点的边画直线.【小练习】
如图5-2-22,过P点画直线c的平行线.知识梳理答案:画图如图5-2-23所示.知识点2:平行线的判定方法.判定方法1:同位角相等,两直线平行.
判定方法2:内错角角相等,两直线平行.
判定方法3:同旁内角互补,两直线平行.知识梳理【例】如图5-2-24,点E在AC的延长线上,下列条件不能判断AB∥CD的是( ).
A.∠3=∠4 B.∠1=∠2 C.∠A=∠DCE D.∠A+∠ACD=180°A知识梳理【讲解】根据图形可知,∠3与∠4是BD与AE被BC所截得到的内错角,由∠3=∠4可以得到BD∥AE;∠1与∠2是AB与CD被BC所截得到的内错角,由∠1=∠2可以得到AB∥CD;∠A=∠DCE是AB与CD被AE所截得到的同位角,由∠A=∠DCE可以得到AB∥CD;∠A与∠ACD是AB与CD被AE所截得到的同旁内角,由∠A+∠ACD=180°可以得到AB∥CD,所以本题的答案应选择A.【方法小结】准确地识别三种角是判断哪两条直线平行的前提条件,一般地“F”形中有同位角,“N”形中有内错角,“U”形中有同旁内角.每一对角的公共边所在的直线是截线,另外两边所在的直线是被截线,即判断平行的两条直线.知识梳理【小练习】
如图5-2-25,在下列条件中:①∠DAC=∠ACB;②∠BAC=∠ACD;③∠BAD+∠ADC=180°;④∠BAD+∠ABC=180°.其中能使直线AB∥CD成立的是__________.(填序号) ②③知识梳理2.如图5-2-26,根据下列条件,可以判定哪两条直线平行?并说明判定的根据是什么.
①∠2=∠B;②∠1=∠D;③∠3+∠F=180°.知识梳理答案:解:①∠2=∠B,可判断AB∥ED,根据“同位角相等,两直线平行”;②∠1=∠D,可判断AC∥FD,根据“内错角相等,两直线平行”;③∠3+∠F=180°,可判断AC∥FD,根据“同旁内角互补,两直线平行”.中考在线
考点:平行线的判定【例1】(2015?黔南州)如图5-2-27,下列说法错误的是( ).
A.若a∥b,b∥c,则a∥c B.若∠1=∠2,则a∥c
C.若∠3=∠2,则b∥c D.若∠3+∠5=180°,则a∥cC知识梳理【解析】根据平行线的判定进行判断:A.若a∥b,b∥c,则a∥c,利用了平行公理,正确;B.若∠1=∠2,则a∥c,利用了内错角相等,两直线平行,正确;C.∠3=∠2,不能判断b∥c,错误;D.若∠3+∠5=180°,则a∥c,利用同旁内角互补,两直线平行,正确;故选C.知识梳理【方法小结】此题考查平行线的判定,关键是根据几种平行线判定的方法进行分析.实战演练
1.(2015?福州)下列图形中,由∠1=∠2能得到AB∥CD的是( ).B知识梳理2.(2014?汕尾)如图5-2-28,能判定EB∥AC的条件是( ).
A.∠C=∠ABE B.∠A=∠EBD C.∠C=∠ABC D.∠A=∠ABED知识梳理3.(2014?湘潭)如图5-2-29,直线a、b被直线c所截,若满足________________________________________,则a、b平行. ∠1=∠2或∠2=∠3或∠3+∠4=180°知识梳理4.(2014?汕尾)已知a,b,c为平面内三条不同直线,若a⊥b,c⊥b,则a与c的位置关系是_______________. 平行课堂练习1.如图5-2-35,己知∠1=145°,∠2=145°,则AB∥CD,依据是___________________________.同位角相等,两直线平行课堂练习2.如图5-2-36 是一条街道的两个拐角,∠ABC与∠BCD均为140°,则街道AB与CD的关系是_________,这是因___________________. 答案:平行;内错角相等,两直线平行。课堂练习3.如图5-2-37一个弯形管道ABCD的拐角∠ABC=120°,∠BCD
=60°,这时说管道AB∥CD,是根据_________________________. 同旁内角互补,两直线平行课堂练习4.如图5-2-38:(1)由∠A=∠3可以判断_____∥_____,根据是____________________________;
(2)由∠2=∠E可以判断_____∥_____,根据是_________________
_______________;
(3)由∠C+∠DBC=180°可以判断______∥______,根据是_____
______________________________.图5-2-38BEAD同位角相等,两直线平行CEBDCEBD内错角相等,两直线平行同旁内角互补,两直线平行答案:(1)AD,BE,同位角相等,两直线平行;(2)BD,CE,内错角相等,两直线平行;(3)BD,CE,同旁内角互补,两直线平行.课堂练习5.如图5-2-39,请完成下列各题:
(1)如果∠1=______,那么DE∥AC(_______________________);
(2)如果∠1=______,那么EF∥BC(_______________________);∠C同位角相等,两直线平行内错角相等,两直线平行∠FED课堂练习(3)如果∠FED+_______=180°,那么AC∥ED(______________
______________);
(4)如果∠2+__________=180°,那么AB∥DF(______________
_______________).∠EFC∠AED同旁内角互补,两直线平行同旁内角互补,两直线平行课堂练习讲评:本题考查的是平行线的判定,根据平行线的判定定理对各选项进行逐一分析即可.6.如图5-2-40,已知:AB∥CD,∠1=∠2,则AB与EF有怎样的位置关系?为什么?课堂练习答案:AB∥EF.因为∠1=∠2,所以CD∥EF,又因为AB∥CD,所以AB∥EF(平行于同一条直线的两条直线互相平行).讲评:本题考查平行线判定方法的灵活使用,以及探究、推理能力.先根据∠1=∠2,得出CD∥EF,再根据AB∥CD,利用平行公理推论解答.7.已知:如图5-2-41,∠BCD=∠B+∠D,试说明AB∥ED.课堂练习答案:如图5-2-42,过点C作∠BCF=∠B,∴AB∥CF.∵∠BCD=∠B+∠D,∠BCD=∠BCF+∠DCF,∴∠DCF=∠D,∴ED∥CF,∴AB∥ED(平行于同一条直线的两条直线互相平行).讲评:本题考查平行线判定方法的应用.解答时,需要添加辅助线,构造角的关系来完成说明.8.如图5-2-43,AB⊥BD,CD⊥MN,垂足分别是B、D点,∠FDC
=∠EBA.
(1)判断CD与AB的位置关系;(2)BE与DF平行吗?为什么?课堂练习答案:(1)CD∥AB,理由是:∵AB⊥BD,∴∠ABD=90°,同理∠CDM=90°,∴∠ABD=∠CDM,∴CD∥AB(同位角相等,两直线平行).
(2)BE∥DF,理由是:∵∠ABD=∠CDM=90°,∠FDC=∠EBA,∴∠ABD-∠EBA=∠CDM-∠FDC,∴∠EBM=∠FDM,∴BE∥DF(同位角相等,两直线平行).课堂练习讲评:解答此类要判定两直线平行的题,可围绕截线找同位角、内错角和同旁内角.(1)利用垂直得一对同位角相等来判断两条直线平行;(2)利用等角的余角相等,得出一对同位角相等来判定两直线平行.课后习题1.如图5-2-44,给出了过直线外一点作已知直线的平行线的方法,其依据是( ).
A.两直线平行,同位角相等 B.内错角相等,两直线平行
C.同旁内角互补,两直线平行 D.同位角相等,两直线平行D课后习题2.用两块相同的三角板按如图5-2-45所示的方式作平行线AB和CD,能解释其中的道理的依据是( )
A.内错角相等,两直线平行 B.同位角相等,两直线平行
C.同旁内角互补,两直线平行 D.平等于同一直线的两直线平行A课后习题3.如图5-2-46,直线a,b都与直线c相交,给出的下列条件:①∠1=∠7;②∠3=∠5;③∠1+∠8=180°;④∠3=∠6.其中能判断a∥b的是( ).
A.①③ B.②③ C.③④ D.①②③D课后习题4.如图5-2-47,下面推理中,正确的是( ).
A.∵∠A+∠D=180°,∴AD∥BC B.∵∠C+∠D=180°,∴AB∥CD
C.∵∠A+∠D=180°,∴AB∥CD D.∵∠A+∠C=180°,∴AB∥CDC课后习题5.如图5-2-48所示,点E在AC的延长线上,下列条件中能判断AB∥CD的是( ).
A.∠3=∠4 B.∠1=∠2 C.∠D=∠DCE
D.∠D+∠ACD=180°B课后习题6.已知:如图5-2-49,∠EAD=∠DCF,要得到AB∥CD,则需要的条件______________.(填一个你认为正确的条件即可)∠EAD=∠B课后习题7.如图5-2-50,BC平分∠DBA,∠1=∠2,填空:因为BC平分∠DBA,所以∠1=_________,所以∠2=___________,所以AB∥
_______.∠CBA∠CBACD课后习题8.已知:如图5-2-51,AB⊥BC,BC⊥CD且∠1=∠2,求证:BE∥CF.答案:证明:∵AB⊥BC,BC⊥CD,∴∠ABC=∠DCB=90°,∵∠1=∠2,∴∠ABC-∠1=∠DCB-∠2,∴∠CBE=∠BCF,∴BE∥CF.课后习题9.如图5-2-52,已知∠1=50°,∠2=65°,CD平分∠ECF,则CD∥FG.请说明理由.课后习题?10.将一副直角三角尺拼成如图5-2-53所示的图形,过点C作CF平分∠DCE交DE于点F,试判断CF与AB是否平行,并说明理由.?课后习题11.如图5-2-54所示,要想判断AB是否与CD平行,我们可以测量哪些角;请你写出三种方案,并说明理由.课后习题答案:解:(1)可以测量∠EAB与∠D,如果∠EAB=∠D,那么根据同位角相等,两直线平行,得出AB与CD平行.(2)可以测量∠BAC与∠C,如果∠BAC=∠C,那么根据内错角相等,两直线平行,得出AB与CD平行.(3)可以测量∠BAD与∠D,如果∠BAD+∠D=180°,那么根据同旁内角互补,两直线平行,得出AB与CD平行.
