北师大版九年级数学下《3.1圆》课件
图片预览







文档简介
课件33张PPT。北师大版九年级下册第三章《圆》3.1 圆学习目标:
理解圆的概念,理解点和圆的位置关系,并能根据条件画出符合条件的点或圆形,初步形成集合的观念;经历形成圆的概念的过程与点和圆位置关系的过程。
学习重点:圆及其有关概念,点与圆的位置关系。
学习难点:用集合的观念描述圆。生活剪影一石激起千层浪奥运五环乐在其中小憩片刻祥子1.从下面的图片中你能发现哪种常见的图形?一、交流预习2.观察车轮,
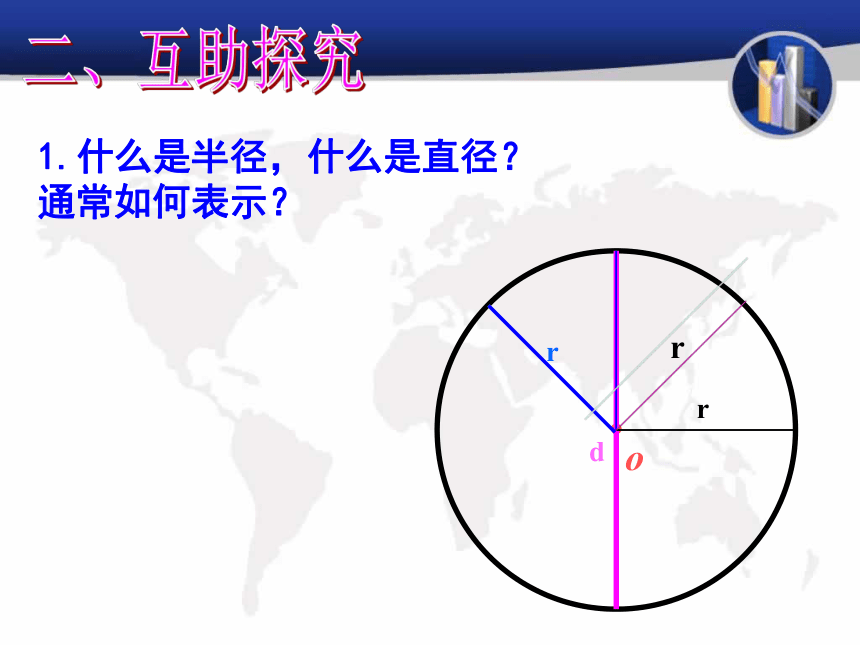
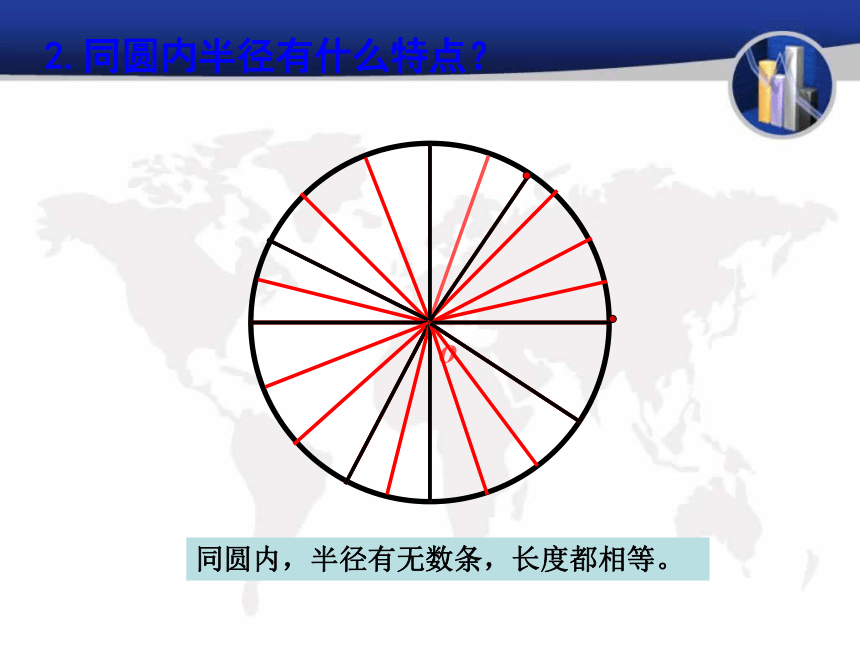
你发现了什么?二、互助探究o?drrr1.什么是半径,什么是直径?通常如何表示?o?同圆内,半径有无数条,长度都相等。2.同圆内半径有什么特点?观察画圆过程回答:(1)圆上各点到定点 (圆心)的距离都等于 。 定长(半径r)(2)到定点的距离等于定长的点都在 。 同一个圆上 圆心为O、半径为r的圆可以看成是所有到定点O的距离等于定长r的点组成的图形。
3.确定一个圆的要素:圆心确定其位置,一是圆心,二是半径,半径确定其大小.
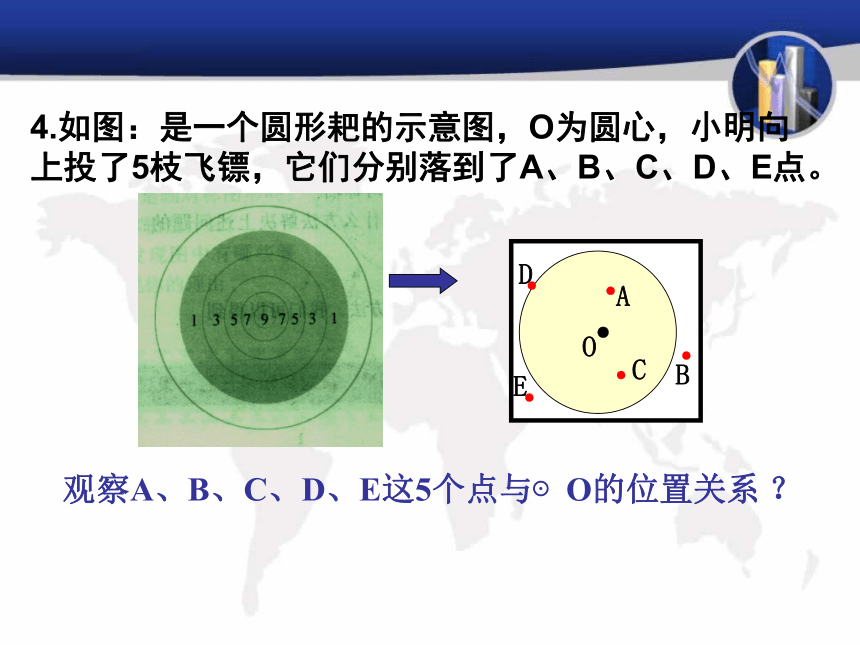
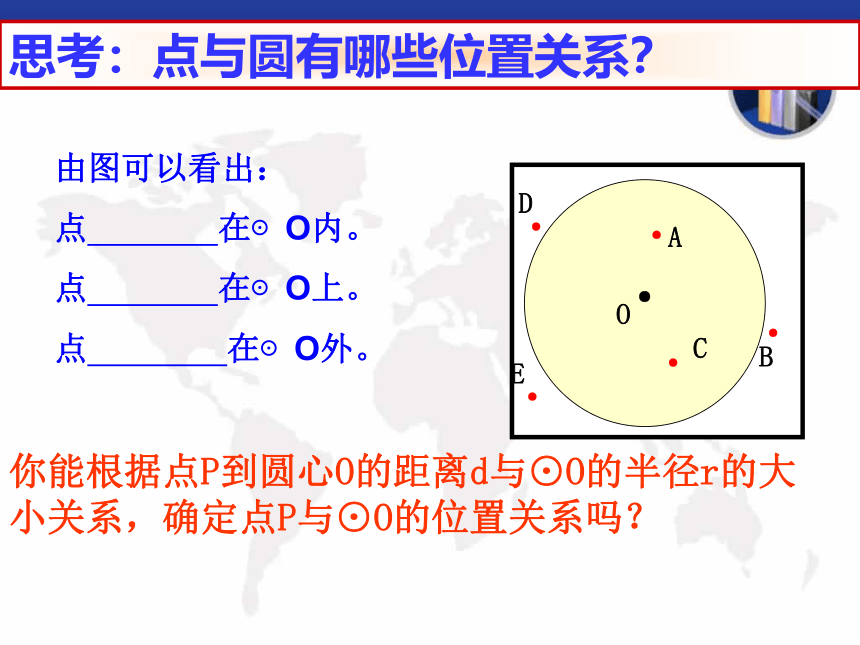
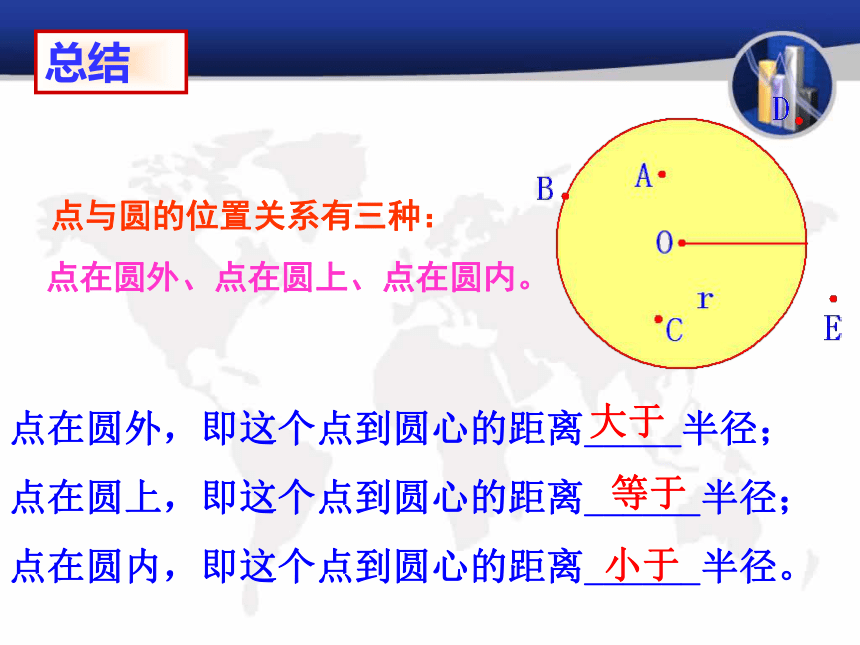
观察A、B、C、D、E这5个点与⊙O的位置关系 ?4.如图:是一个圆形耙的示意图,O为圆心,小明向上投了5枝飞镖,它们分别落到了A、B、C、D、E点。 由图可以看出:
点 在⊙O内。
点 在⊙O上。
点 在⊙O外。你能根据点P到圆心O的距离d与⊙O的半径r的大小关系,确定点P与⊙O的位置关系吗? 点与圆的位置关系有三种:
点在圆外、点在圆上、点在圆内。点在圆外,即这个点到圆心的距离_____半径;
点在圆上,即这个点到圆心的距离______半径;
点在圆内,即这个点到圆心的距离______半径。大于等于小于1、填空:
(1)根据圆的定义,“圆”指的是“ ”,而不是“圆面”。
(2)圆心和半径是确定一个圆的两个必需条件,圆心决定圆的 ,半径决定圆的 ,二者缺一不可。
圆周位置大小三、分层提高 2. 如图所示,一些学生正在做投圈游戏,他们呈“一”字排开。 问题:这样的队形对每一人都公平吗?你认为他们应当排成什么样的队形? 4.已知⊙O的面积为9π,判断点P与⊙O的位置关系.
(1)若PO=4.5,则点P在 ;
(2)若PO=2,则点P在 ;
(3)若PO= ,则点P在圆上. 圆外圆内35.老师现在站住教室中央。我要A同学与我的距离为3m,那么他应当站在哪里呢?是一个固定的位置吗?请同学们通过画图来说明。 . .(1)若现在要求B同学与A同学距离等于2m,那么他应站在哪儿?(2)若现在要求C同学与老师的距离等于2m,那么他又应站在哪儿?老师A6.我现在与A同学的距离为3m:
画图说明下列问题 (4)现在要求B和A与我的距离都小于2m,那么他又应站在哪儿?有几个位置呢? (3)现在要求B同学和A与我的距离都等于2m,那么他又应站在哪儿?有几个位置? . .老师A车轮为什么做成圆形? 7.想 一 想 用这节课学习有关圆的知识来说明为什么
车轮要做成圆形的?中心与路面距离相等
中心与边缘距离相等中心与边缘距离不相等
中心与路面距离不相等 把车轮做成圆形,车轮上各点到车轮中心(圆心)的距离都等于车轮的半径,当车轮在平面上滚动时,车轮中心与平面的距离保持不变,因此,当车辆在平坦的路上行驶时,坐车的人会感到非常平稳,这就是车轮都做成圆形的数学道路。
四、总结归纳通过本节课的学习:
你知道了什么?
最感兴趣的是什么?
学会了哪些方法?
还有哪些疑惑?
还想知道什么?
大家一起分享!师友总结1.如图所示, 一根3m长的绳子,一端栓在柱子上,另一端栓着一只羊,请画出羊的活动区域. 五、巩固提高2.如图所示,一根5m长的绳子,一端栓在柱子上,另一端栓着一只羊,请画出羊的活动区域. 3.如图,一根6m长的绳子,一端栓在柱子上,另一端栓着一只羊,请画出羊的活动区域. 64.如果⊙O的半径为r,点P到圆心O的距离为d,那么:
①点P在⊙O外,则 ______;?
②点P在⊙O外, 则 ———;
③点P在⊙O外, 则 ———.5.如果⊙O的半径为r,点P到圆心O的距离为d,那么:
①___________,则 d>r ;?
②___________, 则 d=r;
③___________, 则 d 古希腊的数学家毕达
哥拉斯认为:“一切立体图
形中最美的是球,一切平面
图形中最美的是圆”。 圆是一种基本的几何图形,圆形物体在生活中随处可见。结束寄语
如果用小圆代表你们学到的知识,用大圆代表我学到的知识,那么大圆的面积是多一点,但两圆之外的空白都是我们的无知面,圆越大其周围接触的无知面就越多。希望同学们努力学习,掌握更多的知识。
一 、回顾本节知识点.
二、 课本后面读一读与试一试
三、 课后习题集
四、 课外收集习题,互相交流
理解圆的概念,理解点和圆的位置关系,并能根据条件画出符合条件的点或圆形,初步形成集合的观念;经历形成圆的概念的过程与点和圆位置关系的过程。
学习重点:圆及其有关概念,点与圆的位置关系。
学习难点:用集合的观念描述圆。生活剪影一石激起千层浪奥运五环乐在其中小憩片刻祥子1.从下面的图片中你能发现哪种常见的图形?一、交流预习2.观察车轮,
你发现了什么?二、互助探究o?drrr1.什么是半径,什么是直径?通常如何表示?o?同圆内,半径有无数条,长度都相等。2.同圆内半径有什么特点?观察画圆过程回答:(1)圆上各点到定点 (圆心)的距离都等于 。 定长(半径r)(2)到定点的距离等于定长的点都在 。 同一个圆上 圆心为O、半径为r的圆可以看成是所有到定点O的距离等于定长r的点组成的图形。
3.确定一个圆的要素:圆心确定其位置,一是圆心,二是半径,半径确定其大小.
观察A、B、C、D、E这5个点与⊙O的位置关系 ?4.如图:是一个圆形耙的示意图,O为圆心,小明向上投了5枝飞镖,它们分别落到了A、B、C、D、E点。 由图可以看出:
点 在⊙O内。
点 在⊙O上。
点 在⊙O外。你能根据点P到圆心O的距离d与⊙O的半径r的大小关系,确定点P与⊙O的位置关系吗? 点与圆的位置关系有三种:
点在圆外、点在圆上、点在圆内。点在圆外,即这个点到圆心的距离_____半径;
点在圆上,即这个点到圆心的距离______半径;
点在圆内,即这个点到圆心的距离______半径。大于等于小于1、填空:
(1)根据圆的定义,“圆”指的是“ ”,而不是“圆面”。
(2)圆心和半径是确定一个圆的两个必需条件,圆心决定圆的 ,半径决定圆的 ,二者缺一不可。
圆周位置大小三、分层提高 2. 如图所示,一些学生正在做投圈游戏,他们呈“一”字排开。 问题:这样的队形对每一人都公平吗?你认为他们应当排成什么样的队形? 4.已知⊙O的面积为9π,判断点P与⊙O的位置关系.
(1)若PO=4.5,则点P在 ;
(2)若PO=2,则点P在 ;
(3)若PO= ,则点P在圆上. 圆外圆内35.老师现在站住教室中央。我要A同学与我的距离为3m,那么他应当站在哪里呢?是一个固定的位置吗?请同学们通过画图来说明。 . .(1)若现在要求B同学与A同学距离等于2m,那么他应站在哪儿?(2)若现在要求C同学与老师的距离等于2m,那么他又应站在哪儿?老师A6.我现在与A同学的距离为3m:
画图说明下列问题 (4)现在要求B和A与我的距离都小于2m,那么他又应站在哪儿?有几个位置呢? (3)现在要求B同学和A与我的距离都等于2m,那么他又应站在哪儿?有几个位置? . .老师A车轮为什么做成圆形? 7.想 一 想 用这节课学习有关圆的知识来说明为什么
车轮要做成圆形的?中心与路面距离相等
中心与边缘距离相等中心与边缘距离不相等
中心与路面距离不相等 把车轮做成圆形,车轮上各点到车轮中心(圆心)的距离都等于车轮的半径,当车轮在平面上滚动时,车轮中心与平面的距离保持不变,因此,当车辆在平坦的路上行驶时,坐车的人会感到非常平稳,这就是车轮都做成圆形的数学道路。
四、总结归纳通过本节课的学习:
你知道了什么?
最感兴趣的是什么?
学会了哪些方法?
还有哪些疑惑?
还想知道什么?
大家一起分享!师友总结1.如图所示, 一根3m长的绳子,一端栓在柱子上,另一端栓着一只羊,请画出羊的活动区域. 五、巩固提高2.如图所示,一根5m长的绳子,一端栓在柱子上,另一端栓着一只羊,请画出羊的活动区域. 3.如图,一根6m长的绳子,一端栓在柱子上,另一端栓着一只羊,请画出羊的活动区域. 64.如果⊙O的半径为r,点P到圆心O的距离为d,那么:
①点P在⊙O外,则 ______;?
②点P在⊙O外, 则 ———;
③点P在⊙O外, 则 ———.5.如果⊙O的半径为r,点P到圆心O的距离为d,那么:
①___________,则 d>r ;?
②___________, 则 d=r;
③___________, 则 d
哥拉斯认为:“一切立体图
形中最美的是球,一切平面
图形中最美的是圆”。 圆是一种基本的几何图形,圆形物体在生活中随处可见。结束寄语
如果用小圆代表你们学到的知识,用大圆代表我学到的知识,那么大圆的面积是多一点,但两圆之外的空白都是我们的无知面,圆越大其周围接触的无知面就越多。希望同学们努力学习,掌握更多的知识。
一 、回顾本节知识点.
二、 课本后面读一读与试一试
三、 课后习题集
四、 课外收集习题,互相交流
