3.4圆周角和圆心角的关系(第2课时)课件
文档属性
| 名称 | 3.4圆周角和圆心角的关系(第2课时)课件 |  | |
| 格式 | zip | ||
| 文件大小 | 436.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-12 19:16:13 | ||
图片预览




文档简介
课件16张PPT。北师大版九年级下册第三章《圆》3.4 圆周角与圆心角的关系(2) 学习目标:
掌握圆周角定理的2个推论的内容,会熟
练运用推论解决问题.
学习重点:圆周角定理的几个推论的应
用.
学习难点:理解几个推论的“题设”和
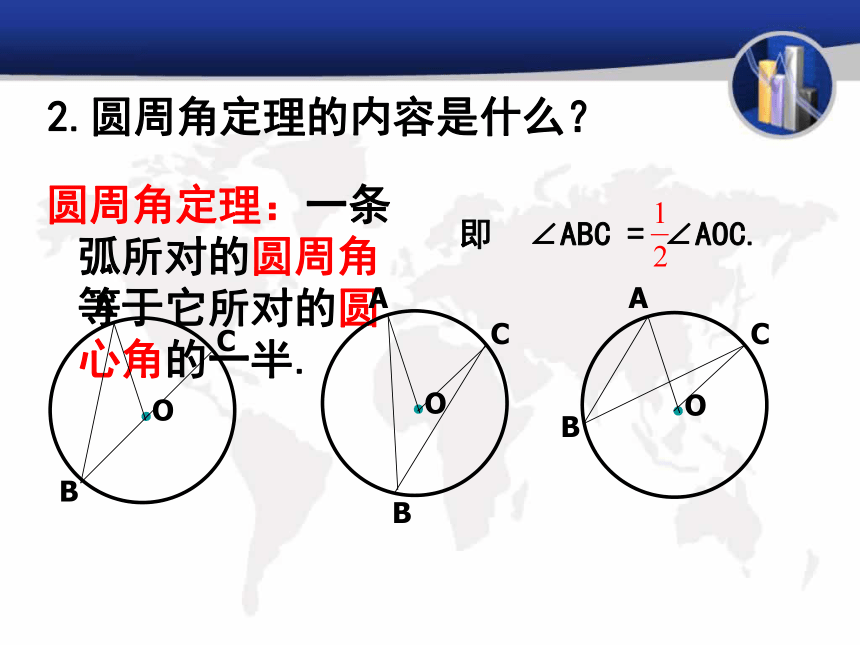
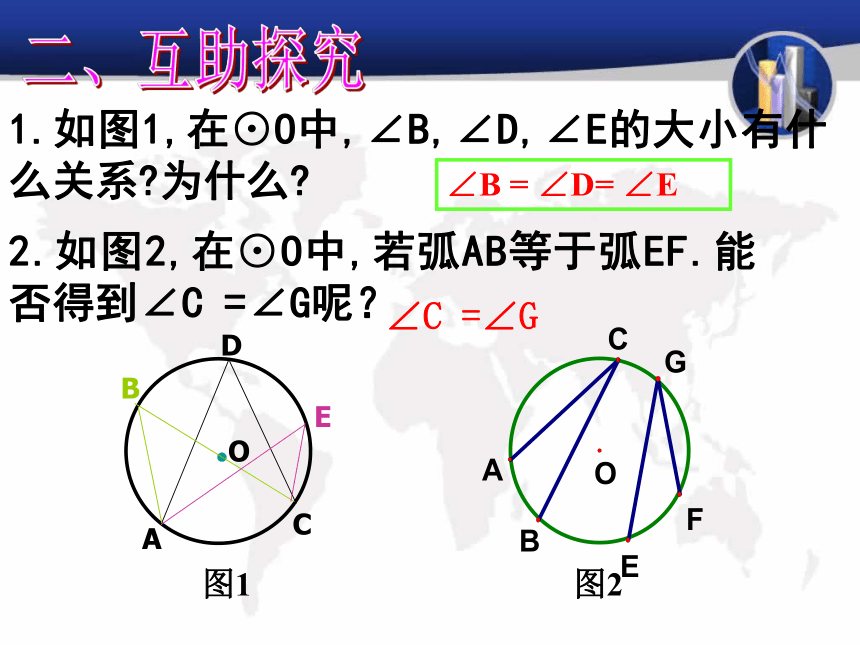
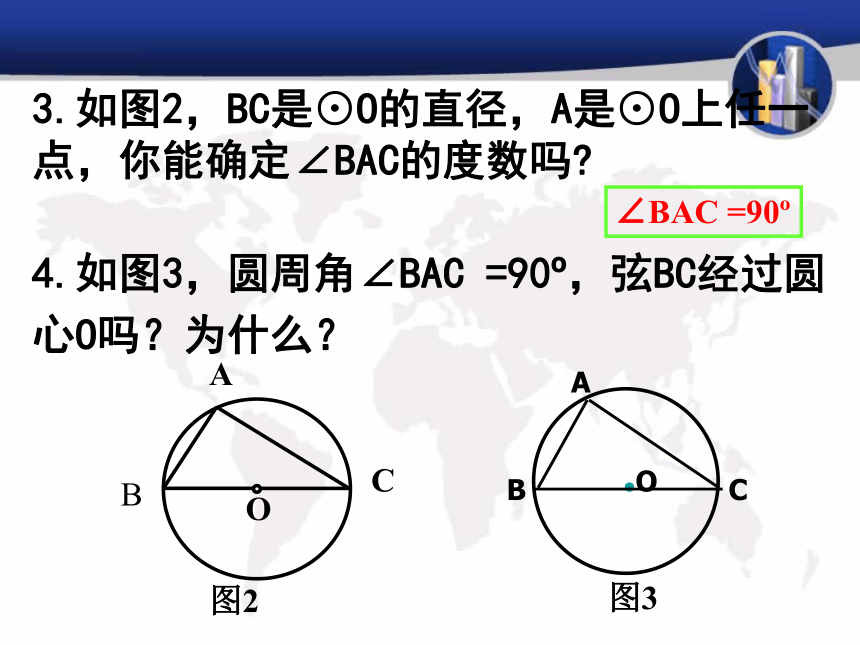
“结论”.特征:① 角的顶点在圆上.② 角的两边都与圆相交.圆周角定义: 顶点在圆上,并且两边都和圆相交的角叫圆周角.1.什么是圆周角?一、交流预习2.圆周角定理的内容是什么?圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半.2.如图2,在⊙O中,若弧AB等于弧EF.能否得到∠C =∠G呢?1.如图1,在⊙O中,∠B,∠D,∠E的大小有什么关系?为什么?∠B = ∠D= ∠E图1∠C =∠G二、互助探究3.如图2,BC是⊙O的直径,A是⊙O上任一点,你能确定∠BAC的度数吗?4.如图3,圆周角∠BAC =90o,弦BC经过圆心O吗?为什么?∠BAC =90o5.问题解答(1)圆周角定理的推论1:同圆或等圆中,同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧也相等.(2)圆周角定理的推论2:用于找相等的角用于找相等的弧用于判断某个圆周角是否是直角用于判断某条线是否过圆心半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径.6.圆内接四边形:1.如图,在⊙O中,∠BAD=50°,求∠C的大小.圆周角定理推论:
圆内接四边形对角互补.2.若∠BAD=80°,求∠C的大小.3.若∠BCD=120°,求∠A的大小.(顶点都在圆上的四边形叫圆内接四边形)证明:连接AD.∵AB是圆的直径,点D在圆上,∴∠ADB=90°,∴AD⊥BC,∵AB=AC,∴AD平分顶角∠BAC,即∠BAD=∠CAD,∴ ⌒ ⌒BD= DE(同圆或等圆中,相等的圆周角所对弧相等)。1.如图.⊙O的直径AB=10cm,C是⊙O上的一点.∠ABC =30°.求AC的长.解:∵ AB是直径∴ ∠ACB= 90o即:AC = 5cm∵∠ABC= 30°∴AC= AB三、分层提高2.小明想用直角尺检查某些工件是否恰好为半圆形. 根据下图, 你能判断哪个是半圆形吗?为什么?四、总结归纳通过本节课的学习:
你知道了什么?
最感兴趣的是什么?
学会了哪些方法?
还有哪些疑惑?
还想知道什么?
大家一起分享!师友总结2.如图,哪个角与∠BAC 相等?1.为什么有些电影院的坐位排列(横排)呈圆弧形?说一说这种设计的合理性?五、巩固提高3.如图,P是△ABC的外接圆上的一点, ∠APC=∠CPB
=60°,求证:△ABC是等边三角形
∴∠ABC=∠APC=60°(同弧所对的圆周角相等)同理,∵∠BAC和∠CPB都是⌒ 所对的圆周角,BC∴∠BAC=∠CPB=60°。∴△ABC等边三角形。4.我手中有一个量角器和一个直角三角尺,你用什么方法可以确定量角器是半圆形? 5.如图,CD是⊙O的直径,弦AB⊥CD于E,那么你能得到什么结论?结论:
(1)AE = BE,AC = BC,AD = BD
(2)AC = BC,∠CAB = ∠ABC = ∠D,
∠ACE =∠BCE =∠DAB
(3)BC2 = AC2 = CE · CD,AD2 = DE · DC
BE2 = AE2 = DE · CE
掌握圆周角定理的2个推论的内容,会熟
练运用推论解决问题.
学习重点:圆周角定理的几个推论的应
用.
学习难点:理解几个推论的“题设”和
“结论”.特征:① 角的顶点在圆上.② 角的两边都与圆相交.圆周角定义: 顶点在圆上,并且两边都和圆相交的角叫圆周角.1.什么是圆周角?一、交流预习2.圆周角定理的内容是什么?圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半.2.如图2,在⊙O中,若弧AB等于弧EF.能否得到∠C =∠G呢?1.如图1,在⊙O中,∠B,∠D,∠E的大小有什么关系?为什么?∠B = ∠D= ∠E图1∠C =∠G二、互助探究3.如图2,BC是⊙O的直径,A是⊙O上任一点,你能确定∠BAC的度数吗?4.如图3,圆周角∠BAC =90o,弦BC经过圆心O吗?为什么?∠BAC =90o5.问题解答(1)圆周角定理的推论1:同圆或等圆中,同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧也相等.(2)圆周角定理的推论2:用于找相等的角用于找相等的弧用于判断某个圆周角是否是直角用于判断某条线是否过圆心半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径.6.圆内接四边形:1.如图,在⊙O中,∠BAD=50°,求∠C的大小.圆周角定理推论:
圆内接四边形对角互补.2.若∠BAD=80°,求∠C的大小.3.若∠BCD=120°,求∠A的大小.(顶点都在圆上的四边形叫圆内接四边形)证明:连接AD.∵AB是圆的直径,点D在圆上,∴∠ADB=90°,∴AD⊥BC,∵AB=AC,∴AD平分顶角∠BAC,即∠BAD=∠CAD,∴ ⌒ ⌒BD= DE(同圆或等圆中,相等的圆周角所对弧相等)。1.如图.⊙O的直径AB=10cm,C是⊙O上的一点.∠ABC =30°.求AC的长.解:∵ AB是直径∴ ∠ACB= 90o即:AC = 5cm∵∠ABC= 30°∴AC= AB三、分层提高2.小明想用直角尺检查某些工件是否恰好为半圆形. 根据下图, 你能判断哪个是半圆形吗?为什么?四、总结归纳通过本节课的学习:
你知道了什么?
最感兴趣的是什么?
学会了哪些方法?
还有哪些疑惑?
还想知道什么?
大家一起分享!师友总结2.如图,哪个角与∠BAC 相等?1.为什么有些电影院的坐位排列(横排)呈圆弧形?说一说这种设计的合理性?五、巩固提高3.如图,P是△ABC的外接圆上的一点, ∠APC=∠CPB
=60°,求证:△ABC是等边三角形
∴∠ABC=∠APC=60°(同弧所对的圆周角相等)同理,∵∠BAC和∠CPB都是⌒ 所对的圆周角,BC∴∠BAC=∠CPB=60°。∴△ABC等边三角形。4.我手中有一个量角器和一个直角三角尺,你用什么方法可以确定量角器是半圆形? 5.如图,CD是⊙O的直径,弦AB⊥CD于E,那么你能得到什么结论?结论:
(1)AE = BE,AC = BC,AD = BD
(2)AC = BC,∠CAB = ∠ABC = ∠D,
∠ACE =∠BCE =∠DAB
(3)BC2 = AC2 = CE · CD,AD2 = DE · DC
BE2 = AE2 = DE · CE
