陕西省榆林市府谷县麻镇中学2016-2017学年高一(上)期末数学试卷(解析版)
文档属性
| 名称 | 陕西省榆林市府谷县麻镇中学2016-2017学年高一(上)期末数学试卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 205.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-13 18:27:08 | ||
图片预览




文档简介
2016-2017学年陕西省榆林市府谷县麻镇中学高一(上)期末数学试卷
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.直线x﹣=0的倾斜角是( )
A.45°
B.60°
C.90°
D.不存在
2.圆x2+y2﹣4x+6y=0的圆心坐标是( )
A.(﹣2,3)
B.(2,3)
C.(﹣2,﹣3)
D.(2,﹣3)
3.已知ac<0,bc<0,则直线ax+by+c=0通过( )
A.第一、二、三象限
B.第一、二、四象限
C.第一、三、四象限
D.第二、三、四象限
4.设m、n是两条不同的直线,α、β是两个不同的平面,则下列命题正确的是( )
A.若m∥α,n∥α,则m∥n
B.若m∥α,m∥β,则α∥β
C.若m∥n,m⊥α,则n⊥α
D.若m∥α,α⊥β,则m⊥β
5.如图所示,在四面体中,若直线EF和GH相交,则它们的交点一定( )
A.在直线DB上
B.在直线AB上
C.在直线CB上
D.都不对
6.已知A(2,5,﹣6),点P在y轴上,|PA|=7,则点P的坐标是( )
A.(0,8,0)
B.(0,2,0)
C.(0,8,0)或(0,2,0)
D.(0,﹣8,0)
7.若直线l经过第二、四象限,则直线l的倾斜角的范围是( )
A.[0°,90°)
B.[0°,180°)
C.[90°,180°)
D.(90°,180°)
8.已知直线l1:ax+2y﹣1=0,直线l2:8x+ay+2﹣a=0,若l1∥l2,则实数a的值为( )
A.±4
B.﹣4
C.4
D.±2
9.已知圆x2+y2+Dx+Ey=0的圆心在直线x+y=l上则D与E的关系是( )
A.D+E=2
B.D+E=1
C.D+E=﹣1
D.D+E=﹣2
10.已知直线a,b,平面α,满足a α,则使b∥α的条件为( )
A.b∥a
B.b∥a且b α
C.a与b异面
D.a与b不相交
11.已知点P(2,1)在圆C:x2+y2+ax﹣2y+b=0上,点P关于直线x+y﹣1=0的对称点也在圆C上,则圆C的圆心坐标为( )
A.(0,1)
B.(1,0)
C.(2,1)
D.(1,2)
12.圆O1:x2+y2﹣2x=0和圆O2:x2+y2﹣4y=0的位置关系是( )
A.相离
B.相交
C.外切
D.内切
二、填空题(每题5分,满分20分,将答案填在答题纸上)
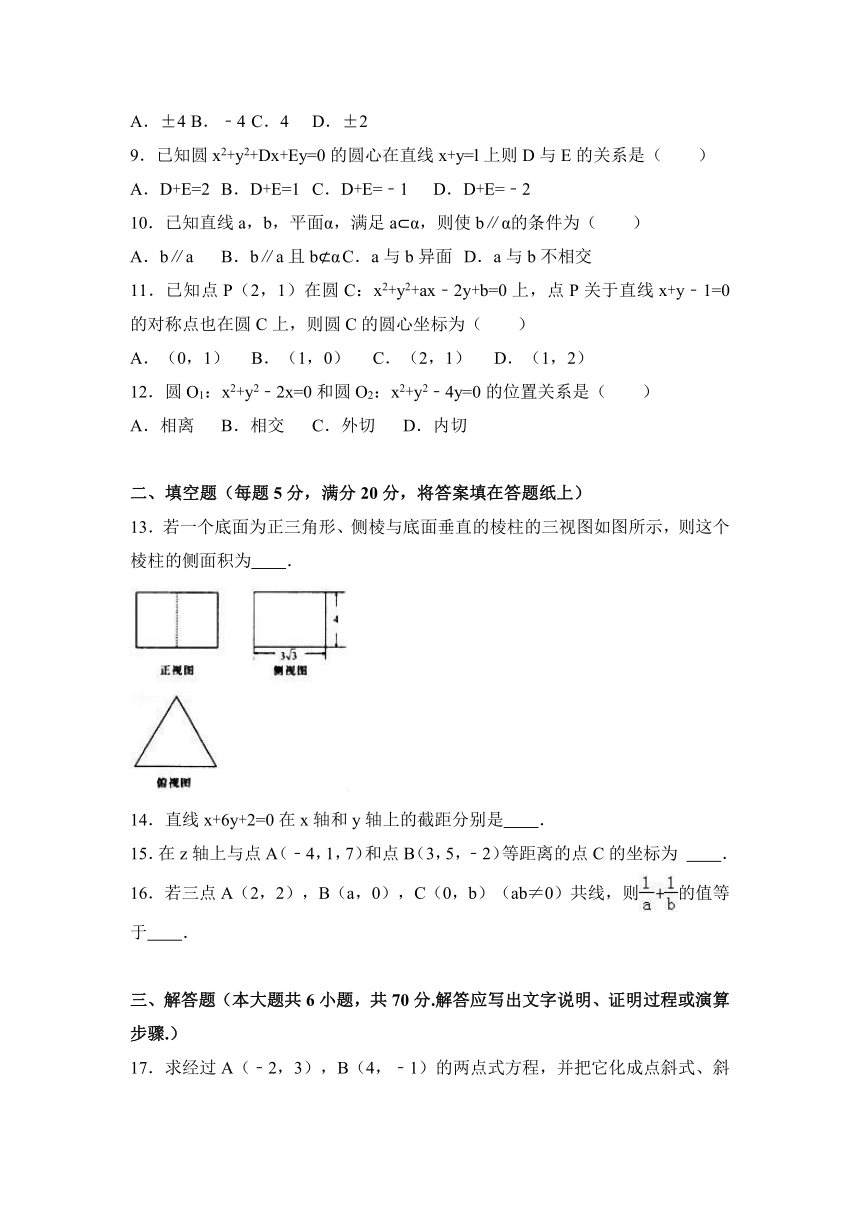
13.若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如图所示,则这个棱柱的侧面积为 .
14.直线x+6y+2=0在x轴和y轴上的截距分别是 .
15.在z轴上与点A(﹣4,1,7)和点B(3,5,﹣2)等距离的点C的坐标为
.
16.若三点A(2,2),B(a,0),C(0,b)(ab≠0)共线,则的值等于 .
三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17.求经过A(﹣2,3),B(4,﹣1)的两点式方程,并把它化成点斜式、斜截式、截距式和一般式.
18.经过两条直线2x+y+2=0和3x+4y﹣2=0的交点,且垂直于直线3x﹣2y+4=0的直线方程为 .
19.如图建立空间直角坐标系,已知正方体的棱长为2.
(1)求正方体各顶点的坐标;
(2)求A1C的长度.
20.已知圆C同时满足下列三个条件:①与y轴相切;②半径为4;③圆心在直线x﹣3y=0上.求圆C的方程.
21.若圆C经过坐标原点和点(4,0),且与直线y=1相切,则圆C的方程是 .
22.如图,在直三棱柱ABC﹣A1B1C1中,A1B1=A1C1,D,E分别是棱BC,CC1上的点(点D
不同于点C),且AD⊥DE,F为B1C1的中点.求证:
(1)平面ADE⊥平面BCC1B1;
(2)直线A1F∥平面ADE.
2016-2017学年陕西省榆林市府谷县麻镇中学高一(上)期末数学试卷
参考答案与试题解析
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.直线x﹣=0的倾斜角是( )
A.45°
B.60°
C.90°
D.不存在
【考点】直线的倾斜角.
【分析】利用直线x﹣=0的斜率不存在,直线和x轴垂直,根据
直线的倾斜角的定义,求出其倾斜角的大小.
【解答】解:直线x﹣=0的斜率不存在,直线和x轴垂直,故倾斜角等于
90°,
故选
C.
2.圆x2+y2﹣4x+6y=0的圆心坐标是( )
A.(﹣2,3)
B.(2,3)
C.(﹣2,﹣3)
D.(2,﹣3)
【考点】圆的标准方程.
【分析】把圆的方程配方得到圆的标准方程后,找出圆心坐标即可.
【解答】解:把圆的方程化为标准方程得:
(x﹣2)2+(y+3)2=13,
所以此圆的圆心坐标为(2,﹣3).
故选D
3.已知ac<0,bc<0,则直线ax+by+c=0通过( )
A.第一、二、三象限
B.第一、二、四象限
C.第一、三、四象限
D.第二、三、四象限
【考点】确定直线位置的几何要素.
【分析】由条件得到直线的斜率和直线的截距,即可得到直线的位置.
【解答】解:直线的斜截式方程为,
∵ac<0,bc<0,
∴ab>0,
即直线的斜率k=,截距,
∴直线ax+by+c=0通过第一,二,四象限.
故选:B.
4.设m、n是两条不同的直线,α、β是两个不同的平面,则下列命题正确的是( )
A.若m∥α,n∥α,则m∥n
B.若m∥α,m∥β,则α∥β
C.若m∥n,m⊥α,则n⊥α
D.若m∥α,α⊥β,则m⊥β
【考点】空间中直线与平面之间的位置关系;空间中直线与直线之间的位置关系;平面与平面之间的位置关系.
【分析】用直线与平面平行的性质定理判断A的正误;用直线与平面平行的性质定理判断B的正误;用线面垂直的判定定理判断C的正误;通过面面垂直的判定定理进行判断D的正误.
【解答】解:A、m∥α,n∥α,则m∥n,m与n可能相交也可能异面,所以A不正确;
B、m∥α,m∥β,则α∥β,还有α与β可能相交,所以B不正确;
C、m∥n,m⊥α,则n⊥α,满足直线与平面垂直的性质定理,故C正确.
D、m∥α,α⊥β,则m⊥β,也可能m∥β,也可能m∩β=A,所以D不正确;
故选C.
5.如图所示,在四面体中,若直线EF和GH相交,则它们的交点一定( )
A.在直线DB上
B.在直线AB上
C.在直线CB上
D.都不对
【考点】平面的基本性质及推论.
【分析】直线EF和GH相交,设交点为M,运用公理2,由此能判断EF与HG的交点在直线BD上.
【解答】解:直线EF和GH相交,设交点为M,
∵EF 平面ABD,HG 平面CBD,
∴M∈平面ABD,且M∈平面CBD,
∵平面ABD∩平面BCD=BD,
∴M∈BD,
∴EF与HG的交点在直线BD上.
故选:A.
6.已知A(2,5,﹣6),点P在y轴上,|PA|=7,则点P的坐标是( )
A.(0,8,0)
B.(0,2,0)
C.(0,8,0)或(0,2,0)
D.(0,﹣8,0)
【考点】空间两点间的距离公式.
【分析】设出P的坐标,利用两点距离公式,求出P的坐标.
【解答】解:由题意设P(0,y,0),
因为|PA|=7,
所以=7,
所以y=2或y=8,
所以点P的坐标为:(0,2,0)或(0,8,0).
故选:C.
7.若直线l经过第二、四象限,则直线l的倾斜角的范围是( )
A.[0°,90°)
B.[0°,180°)
C.[90°,180°)
D.(90°,180°)
【考点】直线的倾斜角.
【分析】由直线l经过第二、四象限,则直线l的斜率小于零,故直线的倾斜角为钝角.
【解答】解:若直线l经过第二、四象限,则直线l的斜率小于零,故直线的倾斜角为钝角,
故选D.
8.已知直线l1:ax+2y﹣1=0,直线l2:8x+ay+2﹣a=0,若l1∥l2,则实数a的值为( )
A.±4
B.﹣4
C.4
D.±2
【考点】直线的一般式方程与直线的平行关系.
【分析】利用直线平行的性质求解.
【解答】解:∵直线l1:ax+2y﹣1=0,直线l2:8x+ay+2﹣a=0,l1∥l2,
∴﹣=﹣,且≠
解得a=﹣4.
故选:B.
9.已知圆x2+y2+Dx+Ey=0的圆心在直线x+y=l上则D与E的关系是( )
A.D+E=2
B.D+E=1
C.D+E=﹣1
D.D+E=﹣2
【考点】直线与圆相交的性质.
【分析】求出圆的圆心坐标,代入直线方程,即可得到D、E的关系.
【解答】解:圆的圆心坐标是(),圆x2+y2+Dx+Ey=0的圆心在直线x+y=l上,所以,即D+E=﹣2.
故选D
10.已知直线a,b,平面α,满足a α,则使b∥α的条件为( )
A.b∥a
B.b∥a且b α
C.a与b异面
D.a与b不相交
【考点】直线与平面平行的性质.
【分析】利用直线与平面平行的判定定理进行判断.
【解答】解:∵a α,
∴b∥a b∥α,或b α,故A不成立;
b∥a且b α b∥α,故B成立;
a与b异面 b∥α或b与α相交,故C不成立;
a与b不相交 b∥α或b α或b与α相交,故D不成立.
故选:B.
11.已知点P(2,1)在圆C:x2+y2+ax﹣2y+b=0上,点P关于直线x+y﹣1=0的对称点也在圆C上,则圆C的圆心坐标为( )
A.(0,1)
B.(1,0)
C.(2,1)
D.(1,2)
【考点】关于点、直线对称的圆的方程.
【分析】根据点P关于直线x+y﹣1=0的对称点也在圆C上,可知圆心在直线x+y﹣1=0上,从而可求a的值,故问题得解.
【解答】解:由题意圆心C(﹣,1)在直线x+y﹣1=0上,从而有﹣+1﹣1=0,∴a=0,
∴圆C的圆心坐标为(0,1),
故选A.
12.圆O1:x2+y2﹣2x=0和圆O2:x2+y2﹣4y=0的位置关系是( )
A.相离
B.相交
C.外切
D.内切
【考点】圆与圆的位置关系及其判定.
【分析】求出半径,求出圆心,看两个圆的圆心距与半径的关系即可.
【解答】解:圆O1:x2+y2﹣2x=0,即(x﹣1)2+y2=1,圆心是O1(1,0),半径是r1=1
圆O2:x2+y2﹣4y=0,即x2+(y﹣2)2=4,圆心是O2(0,2),半径是r2=2
∵|O1O2|=,故|r1﹣r2|<|O1O2|<|r1+r2|
∴两圆的位置关系是相交.
故选
B
二、填空题(每题5分,满分20分,将答案填在答题纸上)
13.若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如图所示,则这个棱柱的侧面积为 72 .
【考点】棱柱、棱锥、棱台的体积;由三视图求面积、体积.
【分析】根据已知中的三视图可求出棱柱的底面周长和高,进而可得棱柱的侧面积.
【解答】解:由已知中的三视图可得:该棱柱的底面高为3,
故该棱柱的底面边长为:6,
故该棱柱的底面周长为:18,
又由棱柱的高h=4,
故棱柱的侧面积为18×4=72,
故答案为:72
14.直线x+6y+2=0在x轴和y轴上的截距分别是 ﹣2,﹣ .
【考点】直线的一般式方程.
【分析】将直线化为截距式方程,即可得到横截距和纵截距或者分别令x=0或y=0也可以进行求解.
【解答】解:方法1:
将直线的方程x+6y+2=0转化截距式方程为:
,
∴在x轴和y轴上的截距分别是﹣2,﹣.
方法2:
∵直线x+6y+2=0,
∴当x=0时,y=﹣,
当y=0时,x=﹣2,
即在x轴和y轴上的截距分别是﹣2,﹣.
故答案为:﹣2,﹣.
15.在z轴上与点A(﹣4,1,7)和点B(3,5,﹣2)等距离的点C的坐标为
(0,0,) .
【考点】空间两点间的距离公式.
【分析】根据C点是z轴上的点,设出C点的坐标(0,0,z),根据C点到A和B的距离相等,写出关于z的方程,解方程即可得到C的竖标,写出点C的坐标.
【解答】解:由题意设C(0,0,z),
∵C与点A(﹣4,1,7)和点B(3,5,﹣2)等距离,
∴|AC|=|BC|,
∴=,
∴18z=28,
∴z=,
∴C点的坐标是(0,0,)
故答案为:(0,0,)
16.若三点A(2,2),B(a,0),C(0,b)(ab≠0)共线,则的值等于 .
【考点】平面向量共线(平行)的坐标表示;平面向量的坐标运算.
【分析】三点共线得两向量共线,用两向量共线的坐标公式列方程求解.
【解答】解:,,
依题意知,
有(a﹣2) (b﹣2)﹣4=0
即ab﹣2a﹣2b=0,变形为ab=2(a+b),
所以==
故答案为
三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17.求经过A(﹣2,3),B(4,﹣1)的两点式方程,并把它化成点斜式、斜截式、截距式和一般式.
【考点】直线的一般式方程;直线的点斜式方程;直线的斜截式方程;直线的截距式方程.
【分析】利用直线方程的求法即可得出.
【解答】解:过A,B两点的直线方程是,
点斜式为:,斜截式为:,
截距式为:,一般式为:2x+3y﹣5=0.
18.经过两条直线2x+y+2=0和3x+4y﹣2=0的交点,且垂直于直线3x﹣2y+4=0的直线方程为 2x+3y﹣2=0 .
【考点】直线的一般式方程与直线的垂直关系.
【分析】联立直线的方程可得交点的坐标,由垂直关系可得所求直线的斜率,由此可得直线的点斜式方程,化为一般式即可.
【解答】解:联立,解之可得,
故可得交点的坐标为(﹣2,2),
又可得直线3x﹣2y+4=0的斜率为,
故所求直线的斜率为﹣,
故可得直线的方程为:y﹣2=﹣(x+2),
化为一般式可得2x+3y﹣2=0.
故答案为:2x+3y﹣2=0.
19.如图建立空间直角坐标系,已知正方体的棱长为2.
(1)求正方体各顶点的坐标;
(2)求A1C的长度.
【考点】空间两点间的距离公式;空间中的点的坐标.
【分析】(1)由已知利用坐标意义即可得出.
(2)解法一:利用两点之间的距离公式即可得出.
解法二:利用勾股定理即可得出.
【解答】解:(1)正方体各顶点的坐标如下:A1(0,0,0),B1(0,2,0),C1(2,2,0),D1(2,0,0),A(0,0,2),B(0,2,2),C(2,2,2),D(2,0,2)
(2)解法一:.
解法二:∵,
在Rt△AA1C1中,,
∴,∴,∴.
20.已知圆C同时满足下列三个条件:①与y轴相切;②半径为4;③圆心在直线x﹣3y=0上.求圆C的方程.
【考点】圆的标准方程.
【分析】根据题意,设圆的圆心为(3b,b),则有|3b|=4,求得b的值,可得圆的标准方程.
【解答】解:∵圆C同时满足下列三个条件:①与y轴相切;②半径为4;③圆心在直线x﹣3y=0上,
设圆的圆心为(3b,b),则|3b|=4,∴b=±,
故要求的圆的方程为(x﹣4)2+=16,或(x+4)2+=16.
21.若圆C经过坐标原点和点(4,0),且与直线y=1相切,则圆C的方程是 .
【考点】圆的标准方程.
【分析】设出圆的圆心坐标与半径,利用已知条件列出方程组,求出圆的圆心坐标与半径,即可得到圆的方程.
【解答】解:设圆的圆心坐标(a,b),半径为r,
因为圆C经过坐标原点和点(4,0),且与直线y=1相切,
所以,
解得,
所求圆的方程为:.
故答案为:.
22.如图,在直三棱柱ABC﹣A1B1C1中,A1B1=A1C1,D,E分别是棱BC,CC1上的点(点D
不同于点C),且AD⊥DE,F为B1C1的中点.求证:
(1)平面ADE⊥平面BCC1B1;
(2)直线A1F∥平面ADE.
【考点】平面与平面垂直的判定;直线与平面平行的判定.
【分析】(1)根据三棱柱ABC﹣A1B1C1是直三棱柱,得到CC1⊥平面ABC,从而AD⊥CC1,结合已知条件AD⊥DE,DE、CC1是平面BCC1B1内的相交直线,得到AD⊥平面BCC1B1,从而平面ADE⊥平面BCC1B1;
(2)先证出等腰三角形△A1B1C1中,A1F⊥B1C1,再用类似(1)的方法,证出A1F⊥平面BCC1B1,结合AD⊥平面BCC1B1,得到A1F∥AD,最后根据线面平行的判定定理,得到直线A1F∥平面ADE.
【解答】解:(1)∵三棱柱ABC﹣A1B1C1是直三棱柱,
∴CC1⊥平面ABC,
∵AD 平面ABC,
∴AD⊥CC1
又∵AD⊥DE,DE、CC1是平面BCC1B1内的相交直线
∴AD⊥平面BCC1B1,
∵AD 平面ADE
∴平面ADE⊥平面BCC1B1;
(2)∵△A1B1C1中,A1B1=A1C1,F为B1C1的中点
∴A1F⊥B1C1,
∵CC1⊥平面A1B1C1,A1F 平面A1B1C1,
∴A1F⊥CC1
又∵B1C1、CC1是平面BCC1B1内的相交直线
∴A1F⊥平面BCC1B1
又∵AD⊥平面BCC1B1,
∴A1F∥AD
∵A1F 平面ADE,AD 平面ADE,
∴直线A1F∥平面ADE.
2017年3月11日
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.直线x﹣=0的倾斜角是( )
A.45°
B.60°
C.90°
D.不存在
2.圆x2+y2﹣4x+6y=0的圆心坐标是( )
A.(﹣2,3)
B.(2,3)
C.(﹣2,﹣3)
D.(2,﹣3)
3.已知ac<0,bc<0,则直线ax+by+c=0通过( )
A.第一、二、三象限
B.第一、二、四象限
C.第一、三、四象限
D.第二、三、四象限
4.设m、n是两条不同的直线,α、β是两个不同的平面,则下列命题正确的是( )
A.若m∥α,n∥α,则m∥n
B.若m∥α,m∥β,则α∥β
C.若m∥n,m⊥α,则n⊥α
D.若m∥α,α⊥β,则m⊥β
5.如图所示,在四面体中,若直线EF和GH相交,则它们的交点一定( )
A.在直线DB上
B.在直线AB上
C.在直线CB上
D.都不对
6.已知A(2,5,﹣6),点P在y轴上,|PA|=7,则点P的坐标是( )
A.(0,8,0)
B.(0,2,0)
C.(0,8,0)或(0,2,0)
D.(0,﹣8,0)
7.若直线l经过第二、四象限,则直线l的倾斜角的范围是( )
A.[0°,90°)
B.[0°,180°)
C.[90°,180°)
D.(90°,180°)
8.已知直线l1:ax+2y﹣1=0,直线l2:8x+ay+2﹣a=0,若l1∥l2,则实数a的值为( )
A.±4
B.﹣4
C.4
D.±2
9.已知圆x2+y2+Dx+Ey=0的圆心在直线x+y=l上则D与E的关系是( )
A.D+E=2
B.D+E=1
C.D+E=﹣1
D.D+E=﹣2
10.已知直线a,b,平面α,满足a α,则使b∥α的条件为( )
A.b∥a
B.b∥a且b α
C.a与b异面
D.a与b不相交
11.已知点P(2,1)在圆C:x2+y2+ax﹣2y+b=0上,点P关于直线x+y﹣1=0的对称点也在圆C上,则圆C的圆心坐标为( )
A.(0,1)
B.(1,0)
C.(2,1)
D.(1,2)
12.圆O1:x2+y2﹣2x=0和圆O2:x2+y2﹣4y=0的位置关系是( )
A.相离
B.相交
C.外切
D.内切
二、填空题(每题5分,满分20分,将答案填在答题纸上)
13.若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如图所示,则这个棱柱的侧面积为 .
14.直线x+6y+2=0在x轴和y轴上的截距分别是 .
15.在z轴上与点A(﹣4,1,7)和点B(3,5,﹣2)等距离的点C的坐标为
.
16.若三点A(2,2),B(a,0),C(0,b)(ab≠0)共线,则的值等于 .
三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17.求经过A(﹣2,3),B(4,﹣1)的两点式方程,并把它化成点斜式、斜截式、截距式和一般式.
18.经过两条直线2x+y+2=0和3x+4y﹣2=0的交点,且垂直于直线3x﹣2y+4=0的直线方程为 .
19.如图建立空间直角坐标系,已知正方体的棱长为2.
(1)求正方体各顶点的坐标;
(2)求A1C的长度.
20.已知圆C同时满足下列三个条件:①与y轴相切;②半径为4;③圆心在直线x﹣3y=0上.求圆C的方程.
21.若圆C经过坐标原点和点(4,0),且与直线y=1相切,则圆C的方程是 .
22.如图,在直三棱柱ABC﹣A1B1C1中,A1B1=A1C1,D,E分别是棱BC,CC1上的点(点D
不同于点C),且AD⊥DE,F为B1C1的中点.求证:
(1)平面ADE⊥平面BCC1B1;
(2)直线A1F∥平面ADE.
2016-2017学年陕西省榆林市府谷县麻镇中学高一(上)期末数学试卷
参考答案与试题解析
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.直线x﹣=0的倾斜角是( )
A.45°
B.60°
C.90°
D.不存在
【考点】直线的倾斜角.
【分析】利用直线x﹣=0的斜率不存在,直线和x轴垂直,根据
直线的倾斜角的定义,求出其倾斜角的大小.
【解答】解:直线x﹣=0的斜率不存在,直线和x轴垂直,故倾斜角等于
90°,
故选
C.
2.圆x2+y2﹣4x+6y=0的圆心坐标是( )
A.(﹣2,3)
B.(2,3)
C.(﹣2,﹣3)
D.(2,﹣3)
【考点】圆的标准方程.
【分析】把圆的方程配方得到圆的标准方程后,找出圆心坐标即可.
【解答】解:把圆的方程化为标准方程得:
(x﹣2)2+(y+3)2=13,
所以此圆的圆心坐标为(2,﹣3).
故选D
3.已知ac<0,bc<0,则直线ax+by+c=0通过( )
A.第一、二、三象限
B.第一、二、四象限
C.第一、三、四象限
D.第二、三、四象限
【考点】确定直线位置的几何要素.
【分析】由条件得到直线的斜率和直线的截距,即可得到直线的位置.
【解答】解:直线的斜截式方程为,
∵ac<0,bc<0,
∴ab>0,
即直线的斜率k=,截距,
∴直线ax+by+c=0通过第一,二,四象限.
故选:B.
4.设m、n是两条不同的直线,α、β是两个不同的平面,则下列命题正确的是( )
A.若m∥α,n∥α,则m∥n
B.若m∥α,m∥β,则α∥β
C.若m∥n,m⊥α,则n⊥α
D.若m∥α,α⊥β,则m⊥β
【考点】空间中直线与平面之间的位置关系;空间中直线与直线之间的位置关系;平面与平面之间的位置关系.
【分析】用直线与平面平行的性质定理判断A的正误;用直线与平面平行的性质定理判断B的正误;用线面垂直的判定定理判断C的正误;通过面面垂直的判定定理进行判断D的正误.
【解答】解:A、m∥α,n∥α,则m∥n,m与n可能相交也可能异面,所以A不正确;
B、m∥α,m∥β,则α∥β,还有α与β可能相交,所以B不正确;
C、m∥n,m⊥α,则n⊥α,满足直线与平面垂直的性质定理,故C正确.
D、m∥α,α⊥β,则m⊥β,也可能m∥β,也可能m∩β=A,所以D不正确;
故选C.
5.如图所示,在四面体中,若直线EF和GH相交,则它们的交点一定( )
A.在直线DB上
B.在直线AB上
C.在直线CB上
D.都不对
【考点】平面的基本性质及推论.
【分析】直线EF和GH相交,设交点为M,运用公理2,由此能判断EF与HG的交点在直线BD上.
【解答】解:直线EF和GH相交,设交点为M,
∵EF 平面ABD,HG 平面CBD,
∴M∈平面ABD,且M∈平面CBD,
∵平面ABD∩平面BCD=BD,
∴M∈BD,
∴EF与HG的交点在直线BD上.
故选:A.
6.已知A(2,5,﹣6),点P在y轴上,|PA|=7,则点P的坐标是( )
A.(0,8,0)
B.(0,2,0)
C.(0,8,0)或(0,2,0)
D.(0,﹣8,0)
【考点】空间两点间的距离公式.
【分析】设出P的坐标,利用两点距离公式,求出P的坐标.
【解答】解:由题意设P(0,y,0),
因为|PA|=7,
所以=7,
所以y=2或y=8,
所以点P的坐标为:(0,2,0)或(0,8,0).
故选:C.
7.若直线l经过第二、四象限,则直线l的倾斜角的范围是( )
A.[0°,90°)
B.[0°,180°)
C.[90°,180°)
D.(90°,180°)
【考点】直线的倾斜角.
【分析】由直线l经过第二、四象限,则直线l的斜率小于零,故直线的倾斜角为钝角.
【解答】解:若直线l经过第二、四象限,则直线l的斜率小于零,故直线的倾斜角为钝角,
故选D.
8.已知直线l1:ax+2y﹣1=0,直线l2:8x+ay+2﹣a=0,若l1∥l2,则实数a的值为( )
A.±4
B.﹣4
C.4
D.±2
【考点】直线的一般式方程与直线的平行关系.
【分析】利用直线平行的性质求解.
【解答】解:∵直线l1:ax+2y﹣1=0,直线l2:8x+ay+2﹣a=0,l1∥l2,
∴﹣=﹣,且≠
解得a=﹣4.
故选:B.
9.已知圆x2+y2+Dx+Ey=0的圆心在直线x+y=l上则D与E的关系是( )
A.D+E=2
B.D+E=1
C.D+E=﹣1
D.D+E=﹣2
【考点】直线与圆相交的性质.
【分析】求出圆的圆心坐标,代入直线方程,即可得到D、E的关系.
【解答】解:圆的圆心坐标是(),圆x2+y2+Dx+Ey=0的圆心在直线x+y=l上,所以,即D+E=﹣2.
故选D
10.已知直线a,b,平面α,满足a α,则使b∥α的条件为( )
A.b∥a
B.b∥a且b α
C.a与b异面
D.a与b不相交
【考点】直线与平面平行的性质.
【分析】利用直线与平面平行的判定定理进行判断.
【解答】解:∵a α,
∴b∥a b∥α,或b α,故A不成立;
b∥a且b α b∥α,故B成立;
a与b异面 b∥α或b与α相交,故C不成立;
a与b不相交 b∥α或b α或b与α相交,故D不成立.
故选:B.
11.已知点P(2,1)在圆C:x2+y2+ax﹣2y+b=0上,点P关于直线x+y﹣1=0的对称点也在圆C上,则圆C的圆心坐标为( )
A.(0,1)
B.(1,0)
C.(2,1)
D.(1,2)
【考点】关于点、直线对称的圆的方程.
【分析】根据点P关于直线x+y﹣1=0的对称点也在圆C上,可知圆心在直线x+y﹣1=0上,从而可求a的值,故问题得解.
【解答】解:由题意圆心C(﹣,1)在直线x+y﹣1=0上,从而有﹣+1﹣1=0,∴a=0,
∴圆C的圆心坐标为(0,1),
故选A.
12.圆O1:x2+y2﹣2x=0和圆O2:x2+y2﹣4y=0的位置关系是( )
A.相离
B.相交
C.外切
D.内切
【考点】圆与圆的位置关系及其判定.
【分析】求出半径,求出圆心,看两个圆的圆心距与半径的关系即可.
【解答】解:圆O1:x2+y2﹣2x=0,即(x﹣1)2+y2=1,圆心是O1(1,0),半径是r1=1
圆O2:x2+y2﹣4y=0,即x2+(y﹣2)2=4,圆心是O2(0,2),半径是r2=2
∵|O1O2|=,故|r1﹣r2|<|O1O2|<|r1+r2|
∴两圆的位置关系是相交.
故选
B
二、填空题(每题5分,满分20分,将答案填在答题纸上)
13.若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如图所示,则这个棱柱的侧面积为 72 .
【考点】棱柱、棱锥、棱台的体积;由三视图求面积、体积.
【分析】根据已知中的三视图可求出棱柱的底面周长和高,进而可得棱柱的侧面积.
【解答】解:由已知中的三视图可得:该棱柱的底面高为3,
故该棱柱的底面边长为:6,
故该棱柱的底面周长为:18,
又由棱柱的高h=4,
故棱柱的侧面积为18×4=72,
故答案为:72
14.直线x+6y+2=0在x轴和y轴上的截距分别是 ﹣2,﹣ .
【考点】直线的一般式方程.
【分析】将直线化为截距式方程,即可得到横截距和纵截距或者分别令x=0或y=0也可以进行求解.
【解答】解:方法1:
将直线的方程x+6y+2=0转化截距式方程为:
,
∴在x轴和y轴上的截距分别是﹣2,﹣.
方法2:
∵直线x+6y+2=0,
∴当x=0时,y=﹣,
当y=0时,x=﹣2,
即在x轴和y轴上的截距分别是﹣2,﹣.
故答案为:﹣2,﹣.
15.在z轴上与点A(﹣4,1,7)和点B(3,5,﹣2)等距离的点C的坐标为
(0,0,) .
【考点】空间两点间的距离公式.
【分析】根据C点是z轴上的点,设出C点的坐标(0,0,z),根据C点到A和B的距离相等,写出关于z的方程,解方程即可得到C的竖标,写出点C的坐标.
【解答】解:由题意设C(0,0,z),
∵C与点A(﹣4,1,7)和点B(3,5,﹣2)等距离,
∴|AC|=|BC|,
∴=,
∴18z=28,
∴z=,
∴C点的坐标是(0,0,)
故答案为:(0,0,)
16.若三点A(2,2),B(a,0),C(0,b)(ab≠0)共线,则的值等于 .
【考点】平面向量共线(平行)的坐标表示;平面向量的坐标运算.
【分析】三点共线得两向量共线,用两向量共线的坐标公式列方程求解.
【解答】解:,,
依题意知,
有(a﹣2) (b﹣2)﹣4=0
即ab﹣2a﹣2b=0,变形为ab=2(a+b),
所以==
故答案为
三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17.求经过A(﹣2,3),B(4,﹣1)的两点式方程,并把它化成点斜式、斜截式、截距式和一般式.
【考点】直线的一般式方程;直线的点斜式方程;直线的斜截式方程;直线的截距式方程.
【分析】利用直线方程的求法即可得出.
【解答】解:过A,B两点的直线方程是,
点斜式为:,斜截式为:,
截距式为:,一般式为:2x+3y﹣5=0.
18.经过两条直线2x+y+2=0和3x+4y﹣2=0的交点,且垂直于直线3x﹣2y+4=0的直线方程为 2x+3y﹣2=0 .
【考点】直线的一般式方程与直线的垂直关系.
【分析】联立直线的方程可得交点的坐标,由垂直关系可得所求直线的斜率,由此可得直线的点斜式方程,化为一般式即可.
【解答】解:联立,解之可得,
故可得交点的坐标为(﹣2,2),
又可得直线3x﹣2y+4=0的斜率为,
故所求直线的斜率为﹣,
故可得直线的方程为:y﹣2=﹣(x+2),
化为一般式可得2x+3y﹣2=0.
故答案为:2x+3y﹣2=0.
19.如图建立空间直角坐标系,已知正方体的棱长为2.
(1)求正方体各顶点的坐标;
(2)求A1C的长度.
【考点】空间两点间的距离公式;空间中的点的坐标.
【分析】(1)由已知利用坐标意义即可得出.
(2)解法一:利用两点之间的距离公式即可得出.
解法二:利用勾股定理即可得出.
【解答】解:(1)正方体各顶点的坐标如下:A1(0,0,0),B1(0,2,0),C1(2,2,0),D1(2,0,0),A(0,0,2),B(0,2,2),C(2,2,2),D(2,0,2)
(2)解法一:.
解法二:∵,
在Rt△AA1C1中,,
∴,∴,∴.
20.已知圆C同时满足下列三个条件:①与y轴相切;②半径为4;③圆心在直线x﹣3y=0上.求圆C的方程.
【考点】圆的标准方程.
【分析】根据题意,设圆的圆心为(3b,b),则有|3b|=4,求得b的值,可得圆的标准方程.
【解答】解:∵圆C同时满足下列三个条件:①与y轴相切;②半径为4;③圆心在直线x﹣3y=0上,
设圆的圆心为(3b,b),则|3b|=4,∴b=±,
故要求的圆的方程为(x﹣4)2+=16,或(x+4)2+=16.
21.若圆C经过坐标原点和点(4,0),且与直线y=1相切,则圆C的方程是 .
【考点】圆的标准方程.
【分析】设出圆的圆心坐标与半径,利用已知条件列出方程组,求出圆的圆心坐标与半径,即可得到圆的方程.
【解答】解:设圆的圆心坐标(a,b),半径为r,
因为圆C经过坐标原点和点(4,0),且与直线y=1相切,
所以,
解得,
所求圆的方程为:.
故答案为:.
22.如图,在直三棱柱ABC﹣A1B1C1中,A1B1=A1C1,D,E分别是棱BC,CC1上的点(点D
不同于点C),且AD⊥DE,F为B1C1的中点.求证:
(1)平面ADE⊥平面BCC1B1;
(2)直线A1F∥平面ADE.
【考点】平面与平面垂直的判定;直线与平面平行的判定.
【分析】(1)根据三棱柱ABC﹣A1B1C1是直三棱柱,得到CC1⊥平面ABC,从而AD⊥CC1,结合已知条件AD⊥DE,DE、CC1是平面BCC1B1内的相交直线,得到AD⊥平面BCC1B1,从而平面ADE⊥平面BCC1B1;
(2)先证出等腰三角形△A1B1C1中,A1F⊥B1C1,再用类似(1)的方法,证出A1F⊥平面BCC1B1,结合AD⊥平面BCC1B1,得到A1F∥AD,最后根据线面平行的判定定理,得到直线A1F∥平面ADE.
【解答】解:(1)∵三棱柱ABC﹣A1B1C1是直三棱柱,
∴CC1⊥平面ABC,
∵AD 平面ABC,
∴AD⊥CC1
又∵AD⊥DE,DE、CC1是平面BCC1B1内的相交直线
∴AD⊥平面BCC1B1,
∵AD 平面ADE
∴平面ADE⊥平面BCC1B1;
(2)∵△A1B1C1中,A1B1=A1C1,F为B1C1的中点
∴A1F⊥B1C1,
∵CC1⊥平面A1B1C1,A1F 平面A1B1C1,
∴A1F⊥CC1
又∵B1C1、CC1是平面BCC1B1内的相交直线
∴A1F⊥平面BCC1B1
又∵AD⊥平面BCC1B1,
∴A1F∥AD
∵A1F 平面ADE,AD 平面ADE,
∴直线A1F∥平面ADE.
2017年3月11日
同课章节目录
