《2.2.2 利用内错角、同旁内角判定两条直线平行》教学课件(20张PPT)
文档属性
| 名称 | 《2.2.2 利用内错角、同旁内角判定两条直线平行》教学课件(20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 111.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-12 00:00:00 | ||
图片预览







文档简介
课件20张PPT。2.2 探索直线平行的条件第二章 相交线与平行线2 利用内错角、同旁内角判定两条直线平行1.理解内错角、同旁内角的概念;
2.结合图形识别内错角、同旁内角;(重点)
3.会运用内错角、同旁内角判定两条直线平行.
(难点)学习目标问题 上节课你学了平行线的哪些内容?如果两条直线都与第三条直线平行,那么这两条直线
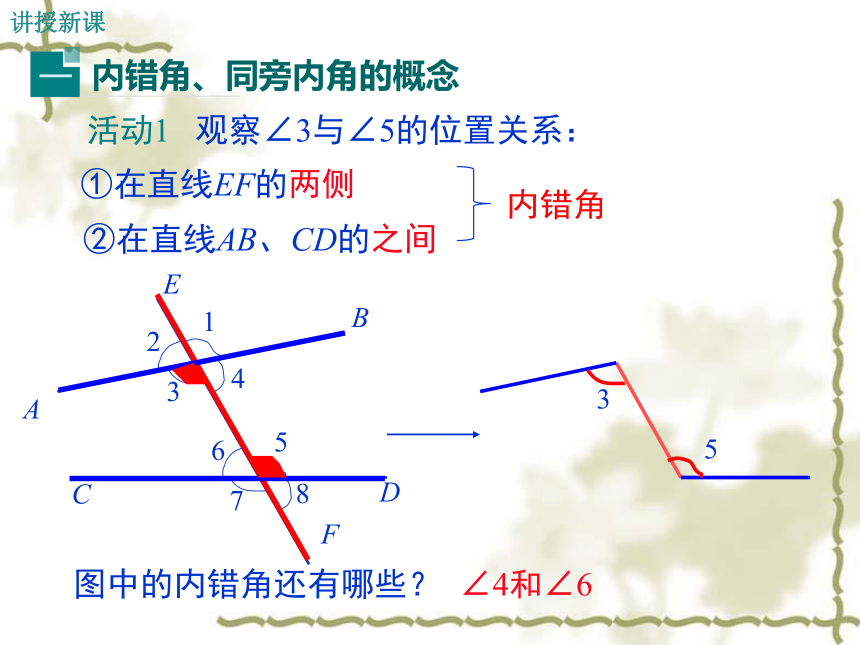
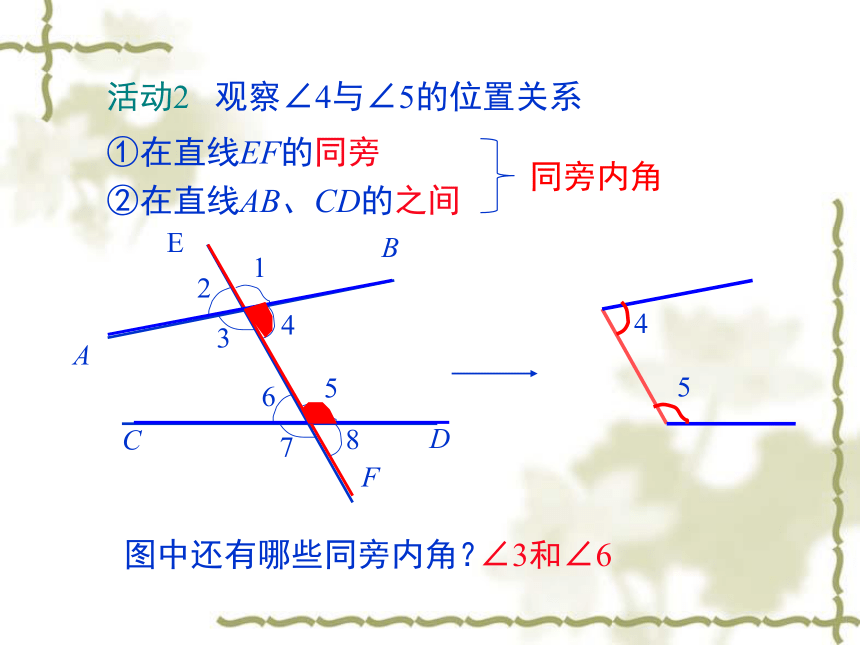
互相平行.经过直线外一点,有且只有一条直线与已知直线平行.导入新课回顾与思考同位角相等,两直线平行.思考 还有其他判定两条直线平行的方法吗?ACBDEF12345678活动1 观察∠3与∠5的位置关系:①在直线EF的两侧②在直线AB、CD的之间∠4和∠6图中的内错角还有哪些?内错角讲授新课变式图形:图中的∠1与∠2都是内错角.图形特征:在形如“Z”的图形中有内错角.ACBDEF12345678活动2 观察∠4与∠5的位置关系①在直线EF的同旁②在直线AB、CD的之间∠3和∠6图中还有哪些同旁内角?同旁内角变式图形:图中的∠1与∠2都是同旁内角.图形特征:在形如“U”的图形中有同旁内角. 之间之间同侧同旁两旁同旁FZU总结归纳 例1 如图,直线DE截AB ,AC,构成8个角,指出所有的同位角,内错角,同旁内角. 解:两条直线是AB,AC,截线是DE,所以8个角中,同位角:∠2与∠5,∠4与∠7,∠1与∠8, ∠6和∠3;内错角:∠4与∠5,∠1与∠6,;同旁内角:∠1与∠5,∠4与∠6.变式:∠A与∠8是哪两条直线被第哪条直线所截的角?它们是什么关系的角?∠A与∠5呢?∠A与∠6呢?EDCBA87654321典例精析 例2 如图,直线DE,BC被直线AB所截.
(1)∠1与∠2, ∠1和∠3,∠1和∠4各是什么角?
解:∠1与∠2是内错角,∠1和∠3同旁内角,∠1和∠4是同旁内角.注意:解题之前要明确哪两条直线被哪条直线所截.解:如果∠1=∠4,由对顶角相等,得∠2=∠4,那么∠1=∠2.因为∠3和∠4互补,即∠4+∠3=180°,又因为∠1=∠4,所以∠4+∠3=180°,即∠1与∠3互补.(2)如果∠1=∠4,那么∠1与∠2相等吗?∠1与∠3互补吗?为什么?问题1 两条直线被第三条直线所截,同时得到同位角、内错角和同旁内角,由同位角相等可以判定两直线平行,那么,能否利用内错角和同旁内角来判定两直线平行呢?如图,由?3=?2,可推出a//b吗?如何推出?解: ∵ ?1=?3(已知),
?3=?2(对顶角相等),
? ?1=?2.
? a//b(同位角相等,两直线平行).判定方法2:两条直线被第三条直线所截 ,如果内错角相等,那么这两条直线平行. 简单说成:内错角相等,两直线平行.∵∠3=∠2(已知)
∴a∥b(内错角相等,两直线平行)应用格式: 总结归纳问题2 如图,如果?1+?2=180° ,你能判定a//b吗?c解:能,
∵?1+?2=180°(已知)
?1+?3=180°(邻补角定义)
??2=?3(同角的补角相等)
?a//b(同位角相等,两直线平行)判定方法3:两条直线被第三条直线所截 ,如果同旁内角互补,那么这两条直线平行. 简单说成:同旁内角互补,两直线平行.应用格式: ∵∠1+∠2=180°(已知)
∴a∥b(内错角相等,两直线平行)总结归纳1.如图,∠1=30°,∠2或∠3满足条件
___________________,则a//b.∠2=150°或∠3=30°当堂练习2.如图.(1)从∠1=∠4,可以推出 ∥ ,
理由是 .(2)从∠ABC +∠ =180°,可以推出AB∥CD ,
理由是 .AB内错角相等,两直线平行CDBCD同旁内角互补,两直线平行3.如图,已知∠1= ∠3,AC平分∠DAB你能判断那两条直线平行?请说明理由?解: AB∥CD. 理由:
∵AC平分∠DAB(已知)
∴∠1=∠2(角平分线定义)
又∵∠1=∠3(已知)
∴∠2=∠3(等量代换)
∴AB∥CD( 内错角相等,两直线平行)1.同位角、内错角、同旁内角的结构特征:三线八角同位角 “F”型内错角 “Z”型同旁内角 “U”型2. 在图形中判断三线八角的方法:描图法: ①把两个角在图中描画出来;②找到两个角的公共直线;③观察所描的角,判断所属“字母”类型,同 位角为“F”型,内错角为“Z”型,同旁内角为“U”型,注意图形的变式(旋转、对称)也是符合的.课堂小结 判定两条直线平行的方法同位角内错角同旁内角∠1=∠2∠3=∠2∠2+∠4=180°abc1243
2.结合图形识别内错角、同旁内角;(重点)
3.会运用内错角、同旁内角判定两条直线平行.
(难点)学习目标问题 上节课你学了平行线的哪些内容?如果两条直线都与第三条直线平行,那么这两条直线
互相平行.经过直线外一点,有且只有一条直线与已知直线平行.导入新课回顾与思考同位角相等,两直线平行.思考 还有其他判定两条直线平行的方法吗?ACBDEF12345678活动1 观察∠3与∠5的位置关系:①在直线EF的两侧②在直线AB、CD的之间∠4和∠6图中的内错角还有哪些?内错角讲授新课变式图形:图中的∠1与∠2都是内错角.图形特征:在形如“Z”的图形中有内错角.ACBDEF12345678活动2 观察∠4与∠5的位置关系①在直线EF的同旁②在直线AB、CD的之间∠3和∠6图中还有哪些同旁内角?同旁内角变式图形:图中的∠1与∠2都是同旁内角.图形特征:在形如“U”的图形中有同旁内角. 之间之间同侧同旁两旁同旁FZU总结归纳 例1 如图,直线DE截AB ,AC,构成8个角,指出所有的同位角,内错角,同旁内角. 解:两条直线是AB,AC,截线是DE,所以8个角中,同位角:∠2与∠5,∠4与∠7,∠1与∠8, ∠6和∠3;内错角:∠4与∠5,∠1与∠6,;同旁内角:∠1与∠5,∠4与∠6.变式:∠A与∠8是哪两条直线被第哪条直线所截的角?它们是什么关系的角?∠A与∠5呢?∠A与∠6呢?EDCBA87654321典例精析 例2 如图,直线DE,BC被直线AB所截.
(1)∠1与∠2, ∠1和∠3,∠1和∠4各是什么角?
解:∠1与∠2是内错角,∠1和∠3同旁内角,∠1和∠4是同旁内角.注意:解题之前要明确哪两条直线被哪条直线所截.解:如果∠1=∠4,由对顶角相等,得∠2=∠4,那么∠1=∠2.因为∠3和∠4互补,即∠4+∠3=180°,又因为∠1=∠4,所以∠4+∠3=180°,即∠1与∠3互补.(2)如果∠1=∠4,那么∠1与∠2相等吗?∠1与∠3互补吗?为什么?问题1 两条直线被第三条直线所截,同时得到同位角、内错角和同旁内角,由同位角相等可以判定两直线平行,那么,能否利用内错角和同旁内角来判定两直线平行呢?如图,由?3=?2,可推出a//b吗?如何推出?解: ∵ ?1=?3(已知),
?3=?2(对顶角相等),
? ?1=?2.
? a//b(同位角相等,两直线平行).判定方法2:两条直线被第三条直线所截 ,如果内错角相等,那么这两条直线平行. 简单说成:内错角相等,两直线平行.∵∠3=∠2(已知)
∴a∥b(内错角相等,两直线平行)应用格式: 总结归纳问题2 如图,如果?1+?2=180° ,你能判定a//b吗?c解:能,
∵?1+?2=180°(已知)
?1+?3=180°(邻补角定义)
??2=?3(同角的补角相等)
?a//b(同位角相等,两直线平行)判定方法3:两条直线被第三条直线所截 ,如果同旁内角互补,那么这两条直线平行. 简单说成:同旁内角互补,两直线平行.应用格式: ∵∠1+∠2=180°(已知)
∴a∥b(内错角相等,两直线平行)总结归纳1.如图,∠1=30°,∠2或∠3满足条件
___________________,则a//b.∠2=150°或∠3=30°当堂练习2.如图.(1)从∠1=∠4,可以推出 ∥ ,
理由是 .(2)从∠ABC +∠ =180°,可以推出AB∥CD ,
理由是 .AB内错角相等,两直线平行CDBCD同旁内角互补,两直线平行3.如图,已知∠1= ∠3,AC平分∠DAB你能判断那两条直线平行?请说明理由?解: AB∥CD. 理由:
∵AC平分∠DAB(已知)
∴∠1=∠2(角平分线定义)
又∵∠1=∠3(已知)
∴∠2=∠3(等量代换)
∴AB∥CD( 内错角相等,两直线平行)1.同位角、内错角、同旁内角的结构特征:三线八角同位角 “F”型内错角 “Z”型同旁内角 “U”型2. 在图形中判断三线八角的方法:描图法: ①把两个角在图中描画出来;②找到两个角的公共直线;③观察所描的角,判断所属“字母”类型,同 位角为“F”型,内错角为“Z”型,同旁内角为“U”型,注意图形的变式(旋转、对称)也是符合的.课堂小结 判定两条直线平行的方法同位角内错角同旁内角∠1=∠2∠3=∠2∠2+∠4=180°abc1243
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
