4.2 图形的全等 课件(14张PPT)
文档属性
| 名称 | 4.2 图形的全等 课件(14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 142.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-12 00:00:00 | ||
图片预览


文档简介
课件14张PPT。4.2 图形的全等第四章 三角形1.了解全等形及全等三角形的概念,掌握全等三
角形的表示方法,理解和掌握全等三角形的性质;
(重点)
2.了解对应边和对应角的概念,能准确找到全等
三角形对应边和对应角;(难点)
3.学生通过观察、发现生活中的全等形和实际操作
中获得全等三角形的体验,在探索和运用全等三
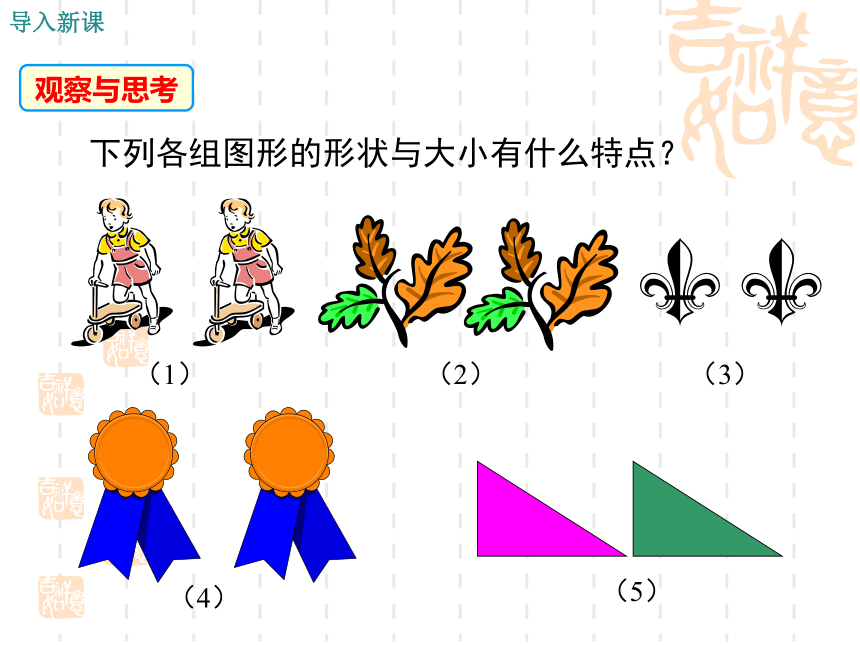
角形性质的过程中感受到数学的乐趣.学习目标导入新课观察与思考下列各组图形的形状与大小有什么特点?(1)(2)(3)(4)(5)一个图形经过平移、旋转、翻折后得到的图形一定与
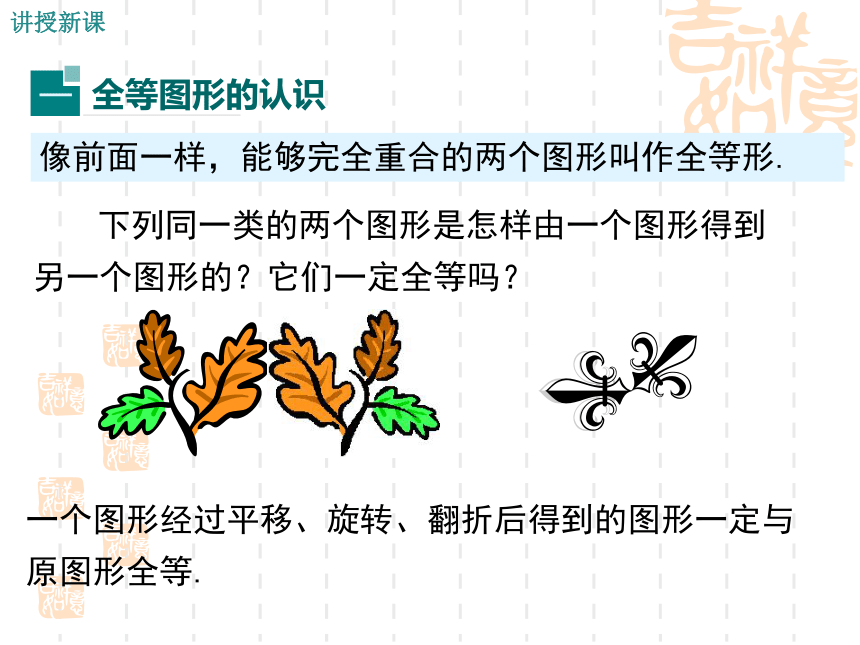
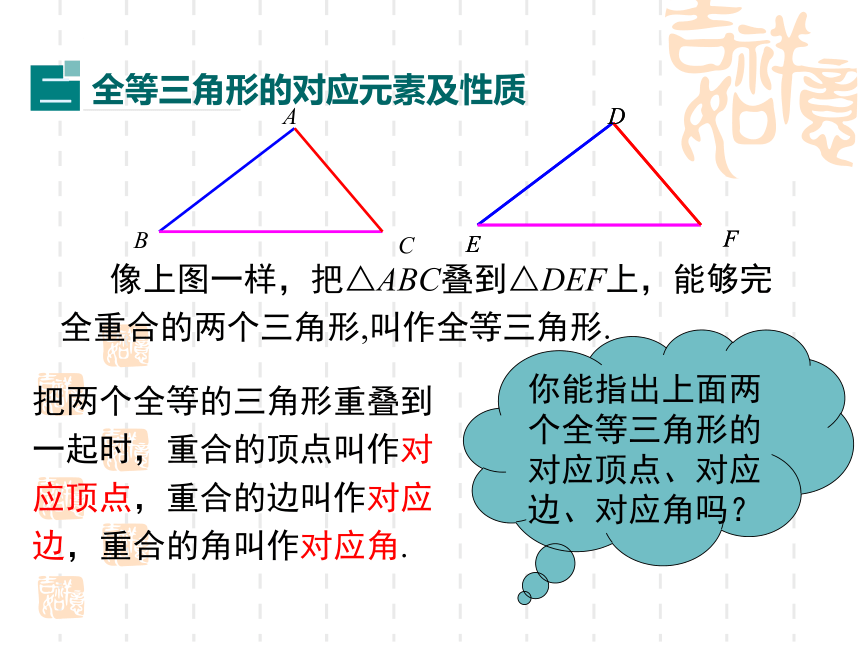
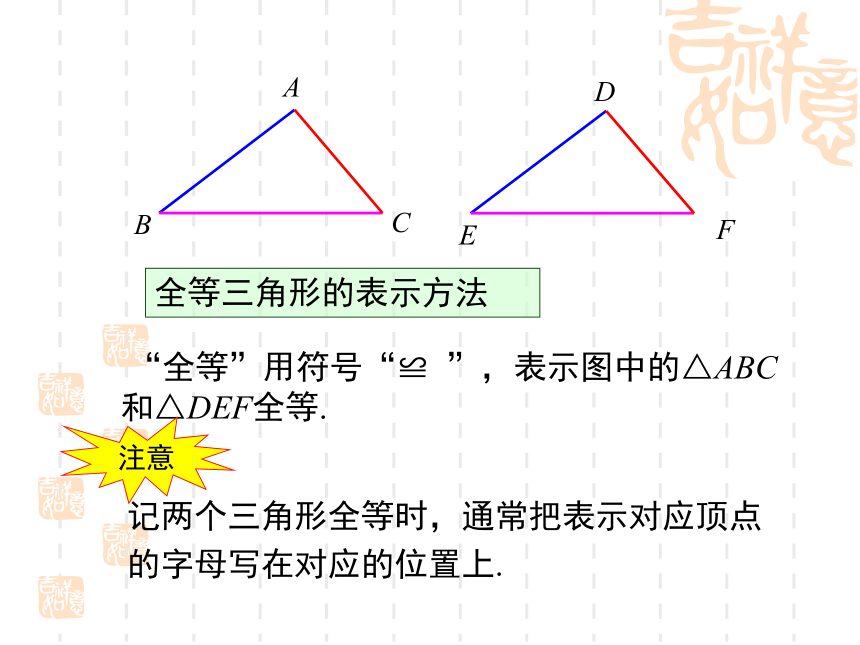
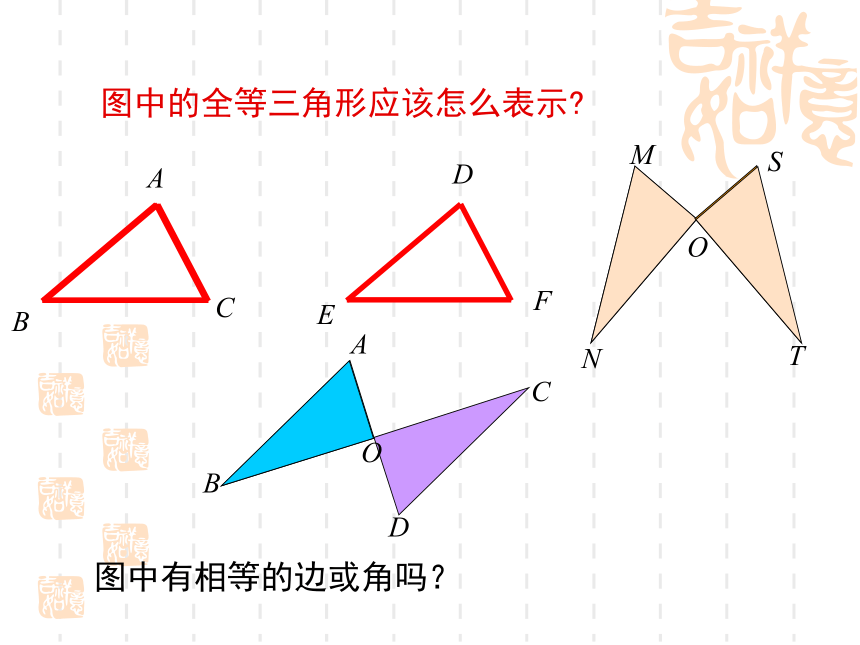
原图形全等. 下列同一类的两个图形是怎样由一个图形得到另一个图形的?它们一定全等吗?像前面一样,能够完全重合的两个图形叫作全等形.讲授新课 像上图一样,把△ABC叠到△DEF上,能够完全重合的两个三角形,叫作全等三角形.把两个全等的三角形重叠到一起时,重合的顶点叫作对应顶点,重合的边叫作对应边,重合的角叫作对应角.你能指出上面两个全等三角形的对应顶点、对应边、对应角吗?A BCEDF “全等”用符号“≌ ”,表示图中的△ABC和△DEF全等.全等三角形的表示方法注意记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.图中的全等三角形应该怎么表示?ABCDEF图中有相等的边或角吗?A BCEDF∵△ABC≌△DEF(已知),∴AB=DE, AC=DF,BC=EF(全等三角形对
应边相等),∠A=∠D, ∠B=∠E, ∠C=∠F(全等三角形对应角相等). 全等三角形的对应边相等;
全等三角形的对应角相等.全等的性质 请你利用自制的一对全等三角形拼出有公共顶点或公共边或公共角的图形.试用全等符号表示它们,分析每个图形,找准对应边、对应角.1.有公共边寻找对应边、对应角有什么规律?探究归纳1. 有公共边,则公共边为对应边;2. 有公共角(对顶角),则公共角(对顶角)为对应角;3.最大边与最大边(最小边与最小边)为对应边;
最大角与最大角(最小角与最小角)为对应角;4. 对应角的对边为对应边;对应边的对角为对应角.2.有公共点总结归纳例 如图,△ABC≌△ CED, ∠ B和∠ DEC是对应角,BC与ED是对应边,说出另两组对应角和对应边.ABCED解: 对应角: ∠ A= ∠ DCE, ∠ D= ∠ ACB; 对应边: AC=CD,AB=CE.典例精析当堂练习1.能够 的两个图形叫做全等形.两个三角形 重合时,互相 的顶点叫做对应顶点.记两个全等三角形时,通常把表示 顶点的字母写在 的位置上.重合重合重合相对应2.如图,△ABC≌ △ADE,若∠D=∠B,
∠C= ∠AED,则∠DAE= ; ∠DAB= . ∠BAC ∠EAC3.如图,△ABC≌△AED,AB是△ABC的最大边,AE是△AED的最大边, ∠BAC 与∠ EAD是对应角,且∠BAC=25°,∠B= 35°,AB=3cm,BC=1cm,求出∠E, ∠ ADE的度数和线段DE,AE 的长度.解:∵ △ABC≌△AED,(已知)∴∠E= ∠B= 35°,(全等三角形对应角
相等)∠ADE=∠ACB=180°-25°-35°
=120 °, (全等三角形对应角相等)DE=BC=1cm, AE=AB=3cm.
(全等三角形对应边相等)全等三角形全等形:能够完全重合的两个图形叫作全等形.课堂小结全等三角形:能够完全重合的两个三角形叫作全等三角形.全等三角形的性质全等三角形的对应边相等全等三角形的对应角相等
角形的表示方法,理解和掌握全等三角形的性质;
(重点)
2.了解对应边和对应角的概念,能准确找到全等
三角形对应边和对应角;(难点)
3.学生通过观察、发现生活中的全等形和实际操作
中获得全等三角形的体验,在探索和运用全等三
角形性质的过程中感受到数学的乐趣.学习目标导入新课观察与思考下列各组图形的形状与大小有什么特点?(1)(2)(3)(4)(5)一个图形经过平移、旋转、翻折后得到的图形一定与
原图形全等. 下列同一类的两个图形是怎样由一个图形得到另一个图形的?它们一定全等吗?像前面一样,能够完全重合的两个图形叫作全等形.讲授新课 像上图一样,把△ABC叠到△DEF上,能够完全重合的两个三角形,叫作全等三角形.把两个全等的三角形重叠到一起时,重合的顶点叫作对应顶点,重合的边叫作对应边,重合的角叫作对应角.你能指出上面两个全等三角形的对应顶点、对应边、对应角吗?A BCEDF “全等”用符号“≌ ”,表示图中的△ABC和△DEF全等.全等三角形的表示方法注意记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.图中的全等三角形应该怎么表示?ABCDEF图中有相等的边或角吗?A BCEDF∵△ABC≌△DEF(已知),∴AB=DE, AC=DF,BC=EF(全等三角形对
应边相等),∠A=∠D, ∠B=∠E, ∠C=∠F(全等三角形对应角相等). 全等三角形的对应边相等;
全等三角形的对应角相等.全等的性质 请你利用自制的一对全等三角形拼出有公共顶点或公共边或公共角的图形.试用全等符号表示它们,分析每个图形,找准对应边、对应角.1.有公共边寻找对应边、对应角有什么规律?探究归纳1. 有公共边,则公共边为对应边;2. 有公共角(对顶角),则公共角(对顶角)为对应角;3.最大边与最大边(最小边与最小边)为对应边;
最大角与最大角(最小角与最小角)为对应角;4. 对应角的对边为对应边;对应边的对角为对应角.2.有公共点总结归纳例 如图,△ABC≌△ CED, ∠ B和∠ DEC是对应角,BC与ED是对应边,说出另两组对应角和对应边.ABCED解: 对应角: ∠ A= ∠ DCE, ∠ D= ∠ ACB; 对应边: AC=CD,AB=CE.典例精析当堂练习1.能够 的两个图形叫做全等形.两个三角形 重合时,互相 的顶点叫做对应顶点.记两个全等三角形时,通常把表示 顶点的字母写在 的位置上.重合重合重合相对应2.如图,△ABC≌ △ADE,若∠D=∠B,
∠C= ∠AED,则∠DAE= ; ∠DAB= . ∠BAC ∠EAC3.如图,△ABC≌△AED,AB是△ABC的最大边,AE是△AED的最大边, ∠BAC 与∠ EAD是对应角,且∠BAC=25°,∠B= 35°,AB=3cm,BC=1cm,求出∠E, ∠ ADE的度数和线段DE,AE 的长度.解:∵ △ABC≌△AED,(已知)∴∠E= ∠B= 35°,(全等三角形对应角
相等)∠ADE=∠ACB=180°-25°-35°
=120 °, (全等三角形对应角相等)DE=BC=1cm, AE=AB=3cm.
(全等三角形对应边相等)全等三角形全等形:能够完全重合的两个图形叫作全等形.课堂小结全等三角形:能够完全重合的两个三角形叫作全等三角形.全等三角形的性质全等三角形的对应边相等全等三角形的对应角相等
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
