4.1.1 三角形的内角和 课件(26张PPT)
文档属性
| 名称 | 4.1.1 三角形的内角和 课件(26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 560.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-12 23:47:06 | ||
图片预览





文档简介
课件26张PPT。4.1 认识三角形第四章 三角形1 三角形的内角和1.了解三角形及相关概念,能正确识别和表示三角形;
2. 会按角的大小对三角形进行分类;
3.掌握三角形的内角和等于180°,并会据此解决简单
的问题.(重点、难点)学习目标导入新课图片导入你能在图中找到三角形吗?在我们的生活中还有
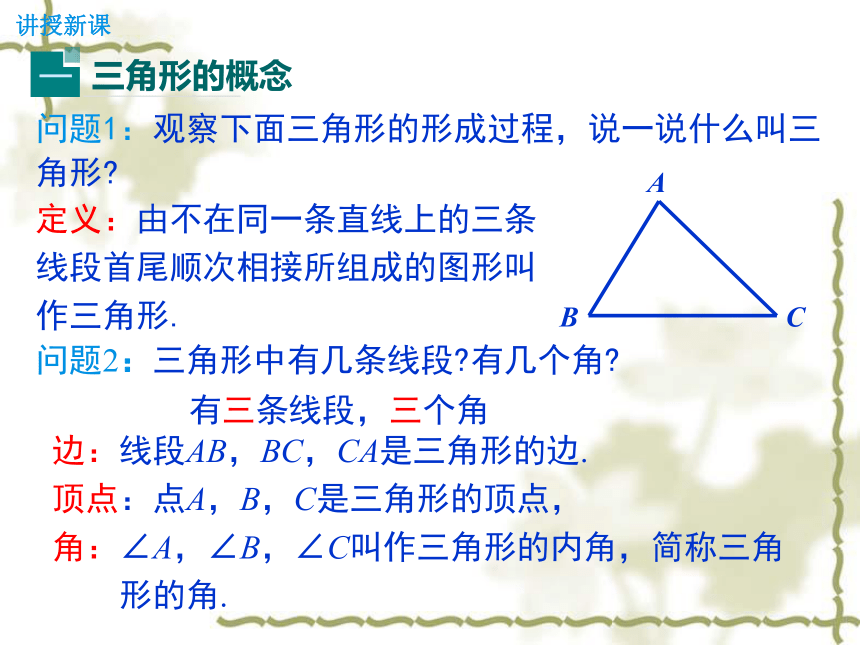
没有这样的图形呢?试举例.讲授新课问题1:观察下面三角形的形成过程,说一说什么叫三角形?定义:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫作三角形.问题2:三角形中有几条线段?有几个角?A B C 边:线段AB,BC,CA是三角形的边.
顶点:点A,B,C是三角形的顶点,
角:∠A,∠B,∠C叫作三角形的内角,简称三角
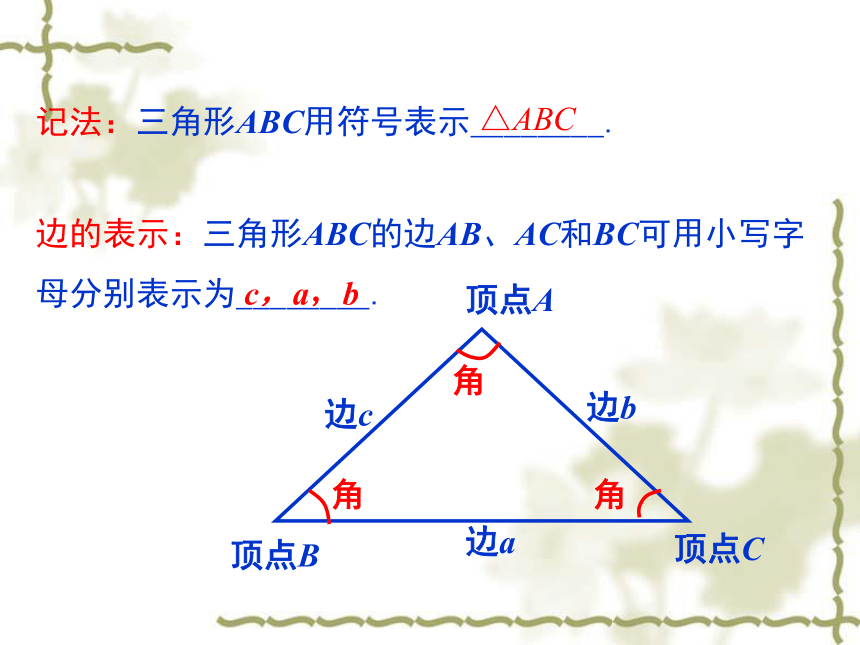
形的角. 有三条线段,三个角记法:三角形ABC用符号表示________.
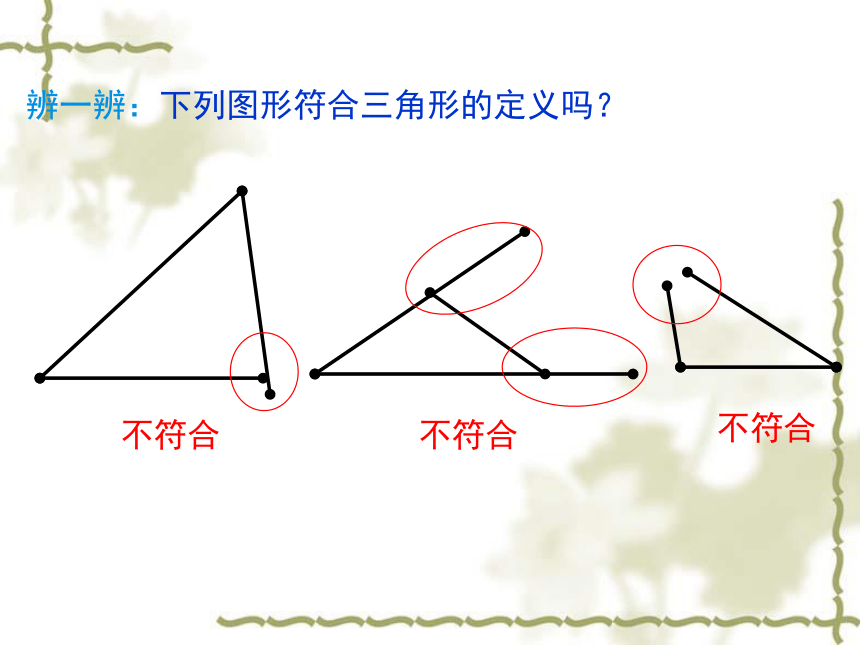
边的表示:三角形ABC的边AB、AC和BC可用小写字母分别表示为________.△ABCc,a,b边c边b边a顶点C角角角顶点A顶点B辨一辨:下列图形符合三角形的定义吗?不符合不符合不符合①位置关系:不在同一直线上;
②联接方式:首尾顺次相接.三角形应满足以下两个条件:要点提醒表示方法:
三角形用符号“△”表示;记作“△ABC”,读作“三角形ABC”,除此△ABC还可记作△BCA,
△ CAB, △ ACB等.基本要素:
三角形的边:边AB、BC、CA;
三角形的顶点:顶点A、B、C;
三角形的内角(简称为三角形的角):∠ A、 ∠ B、 ∠ C.特别规定:
三角形ABC的三边,一般的顶点A所对的边记作a,顶点B所对的边记作b,顶点C所对的边记作c.5个,它们分别是△ABE,△ABC, △BEC,△BCD,△ECD.找一找:(1)图中有几个三角形?用符号表示出这些三角形? (2)以AB为边的三角形有哪些?△ABC、△ABE.(3)以E为顶点的三角形有哪些?△ ABE 、△BCE、 △CDE.(4)以∠D为角的三角形有哪些?△ BCD、 △DEC.(5)说出△BCD的三个角和三个顶点所对的边.△BCD的三个角是∠BCD、∠BDC、∠CBD.顶点B所对应的边为DC,顶点C所对应的边为BD,顶点D所对应的边为BC.内角三兄弟之争 在一个直角三角形里住着三个内角,平时,它们三兄弟非常团结.可是有一天,老二突然不高兴,发起脾气来,它指着老大说:“你凭什么度数最大,我也要和你一样大!”“不行啊!”老大说:“这是不可能的,否则,我们这个家就再也围不起来了……”“为什么?” 老二很纳闷.
同学们,你们知道其中的道理吗?三角形的三个内角和是多少?有什么办法可以验证呢?想一想结论:三角形三个内角的和等于180°. 例1 已知,如图,D是△ABC中BC边延长线上一点,F为AB上一点,直线FD交AC于E,∠DFB=90°,∠A=46°,∠D=50°.求∠ACB的度数.解:在△DFB中,∵∠DFB=90°,∠D=50°,
∠DFB+∠D+∠B=180°,∴∠B=40°.
在△ABC中,∵∠A=46°,∠B=40°,
∴∠ACB=180°-∠A-∠B=94°.典例精析 同学们手中有直角三角板,请再画一个内角都不是90°的三角形.三个角都是锐角的三角形叫作锐角三角形;锐角三角形有一个角是钝角的三角形叫作钝角三角形.钝角三角形有一个角是直角的三角形叫作直角三角形;直角三角形直角边直角边斜边ABC直角三角形ABC可以写成Rt△ABC;直角三角形锐角三角形钝角三角形三角形三角形按角的大小分类根据“三角形的内角和为180°”易得“直角三角形的两个锐角互余”.例2 一个三角形的三个内角的度数之比为1∶2∶3,这个三角形一定是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.无法判定解析:设这个三角形的三个内角的度数分别是x,2x,3x,根据三角形的内角和为180°,得x+2x+3x=180°,解得x=30°,∴这个三角形的三个内角的度数分别是30°,60°,90°,即这个三角形是直角三角形.典例精析A例3 如图,CE⊥AF,垂足为E,CE与BF相交于点D,∠F=40°,∠C=30°,求∠EDF、∠DBC的度数.解:∵CE⊥AF,∴∠DEF=90°,
∴∠EDF=90°-∠F=90°-40°
=50°.由三角形的内角和定理得∠C
+∠DBC+∠CDB=∠F+∠DEF
+∠EDF,又∵∠CDB=∠EDF,
∴30°+∠DBC=40°+90°,
∴∠DBC=100°.1.三角形是指( )
A.由三条线段所组成的封闭图形
B.由不在同一直线上的三条直线首尾顺次相
接组成的图形
C.由不在同一直线上的三条线段首尾顺次相
接组成的图形
D.由三条线段首尾顺次相接组成的图形C当堂练习2.(口答)下列各组角是同一个三角形的内角
吗?为什么?(2)60°, 40°, 90°(3)30°, 60°, 50°(1)3°, 150°, 27° 是 不是不是提醒:三角形的内角和为180°.3.(1)在△ABC中,∠A=35°,∠ B=43°,
则∠ C =_______;(2)在△ABC中,∠C=90°,∠B=50°,
则∠A = _______;(3)在△ABC中, ∠A=40°,∠A=2∠B,
则∠C = ________.102°40°120°4.在△ABC中,∠A的度数是∠B的度数的3倍,
∠C 比∠B 大15°,求∠A,∠B,∠C的度数. 设∠B为x °,则∠A为(3x)°,∠C为(x+ 15)°. 3x+x+(x+15)=180,解得 x=33.所以 3x=99 ,x+15 =48.即∠A,∠B,∠C的度数分别为99°,33°,48°.根据三角形的内角和等于180°, 得解: 5.如图,△ABC中BD⊥AC,垂足为D,∠ABD=54°,
∠DBC=18°,求∠A和∠C的度数.∵∠A+∠ABD+∠ADB=180°,∵BD⊥AC,∴∠ADB=∠CDB=90°.∠ABD=54°,∠ADB=90°,∴∠A=180°-∠ABD-∠ADB=180°-54°-90°=36°.解:∠C=180°-∠A-(∠ABD+∠DBC)=180°-36°-(54°+18°)=72°.三角形三角形的概念:由不在同一条直线上的三条线段首尾依次相接所组成的封闭图形.课堂小结三角形按角分类直角三角形锐角三角形钝角三角形三角形的内角和等于180°直角三角形的两个锐角互余
2. 会按角的大小对三角形进行分类;
3.掌握三角形的内角和等于180°,并会据此解决简单
的问题.(重点、难点)学习目标导入新课图片导入你能在图中找到三角形吗?在我们的生活中还有
没有这样的图形呢?试举例.讲授新课问题1:观察下面三角形的形成过程,说一说什么叫三角形?定义:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫作三角形.问题2:三角形中有几条线段?有几个角?A B C 边:线段AB,BC,CA是三角形的边.
顶点:点A,B,C是三角形的顶点,
角:∠A,∠B,∠C叫作三角形的内角,简称三角
形的角. 有三条线段,三个角记法:三角形ABC用符号表示________.
边的表示:三角形ABC的边AB、AC和BC可用小写字母分别表示为________.△ABCc,a,b边c边b边a顶点C角角角顶点A顶点B辨一辨:下列图形符合三角形的定义吗?不符合不符合不符合①位置关系:不在同一直线上;
②联接方式:首尾顺次相接.三角形应满足以下两个条件:要点提醒表示方法:
三角形用符号“△”表示;记作“△ABC”,读作“三角形ABC”,除此△ABC还可记作△BCA,
△ CAB, △ ACB等.基本要素:
三角形的边:边AB、BC、CA;
三角形的顶点:顶点A、B、C;
三角形的内角(简称为三角形的角):∠ A、 ∠ B、 ∠ C.特别规定:
三角形ABC的三边,一般的顶点A所对的边记作a,顶点B所对的边记作b,顶点C所对的边记作c.5个,它们分别是△ABE,△ABC, △BEC,△BCD,△ECD.找一找:(1)图中有几个三角形?用符号表示出这些三角形? (2)以AB为边的三角形有哪些?△ABC、△ABE.(3)以E为顶点的三角形有哪些?△ ABE 、△BCE、 △CDE.(4)以∠D为角的三角形有哪些?△ BCD、 △DEC.(5)说出△BCD的三个角和三个顶点所对的边.△BCD的三个角是∠BCD、∠BDC、∠CBD.顶点B所对应的边为DC,顶点C所对应的边为BD,顶点D所对应的边为BC.内角三兄弟之争 在一个直角三角形里住着三个内角,平时,它们三兄弟非常团结.可是有一天,老二突然不高兴,发起脾气来,它指着老大说:“你凭什么度数最大,我也要和你一样大!”“不行啊!”老大说:“这是不可能的,否则,我们这个家就再也围不起来了……”“为什么?” 老二很纳闷.
同学们,你们知道其中的道理吗?三角形的三个内角和是多少?有什么办法可以验证呢?想一想结论:三角形三个内角的和等于180°. 例1 已知,如图,D是△ABC中BC边延长线上一点,F为AB上一点,直线FD交AC于E,∠DFB=90°,∠A=46°,∠D=50°.求∠ACB的度数.解:在△DFB中,∵∠DFB=90°,∠D=50°,
∠DFB+∠D+∠B=180°,∴∠B=40°.
在△ABC中,∵∠A=46°,∠B=40°,
∴∠ACB=180°-∠A-∠B=94°.典例精析 同学们手中有直角三角板,请再画一个内角都不是90°的三角形.三个角都是锐角的三角形叫作锐角三角形;锐角三角形有一个角是钝角的三角形叫作钝角三角形.钝角三角形有一个角是直角的三角形叫作直角三角形;直角三角形直角边直角边斜边ABC直角三角形ABC可以写成Rt△ABC;直角三角形锐角三角形钝角三角形三角形三角形按角的大小分类根据“三角形的内角和为180°”易得“直角三角形的两个锐角互余”.例2 一个三角形的三个内角的度数之比为1∶2∶3,这个三角形一定是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.无法判定解析:设这个三角形的三个内角的度数分别是x,2x,3x,根据三角形的内角和为180°,得x+2x+3x=180°,解得x=30°,∴这个三角形的三个内角的度数分别是30°,60°,90°,即这个三角形是直角三角形.典例精析A例3 如图,CE⊥AF,垂足为E,CE与BF相交于点D,∠F=40°,∠C=30°,求∠EDF、∠DBC的度数.解:∵CE⊥AF,∴∠DEF=90°,
∴∠EDF=90°-∠F=90°-40°
=50°.由三角形的内角和定理得∠C
+∠DBC+∠CDB=∠F+∠DEF
+∠EDF,又∵∠CDB=∠EDF,
∴30°+∠DBC=40°+90°,
∴∠DBC=100°.1.三角形是指( )
A.由三条线段所组成的封闭图形
B.由不在同一直线上的三条直线首尾顺次相
接组成的图形
C.由不在同一直线上的三条线段首尾顺次相
接组成的图形
D.由三条线段首尾顺次相接组成的图形C当堂练习2.(口答)下列各组角是同一个三角形的内角
吗?为什么?(2)60°, 40°, 90°(3)30°, 60°, 50°(1)3°, 150°, 27° 是 不是不是提醒:三角形的内角和为180°.3.(1)在△ABC中,∠A=35°,∠ B=43°,
则∠ C =_______;(2)在△ABC中,∠C=90°,∠B=50°,
则∠A = _______;(3)在△ABC中, ∠A=40°,∠A=2∠B,
则∠C = ________.102°40°120°4.在△ABC中,∠A的度数是∠B的度数的3倍,
∠C 比∠B 大15°,求∠A,∠B,∠C的度数. 设∠B为x °,则∠A为(3x)°,∠C为(x+ 15)°. 3x+x+(x+15)=180,解得 x=33.所以 3x=99 ,x+15 =48.即∠A,∠B,∠C的度数分别为99°,33°,48°.根据三角形的内角和等于180°, 得解: 5.如图,△ABC中BD⊥AC,垂足为D,∠ABD=54°,
∠DBC=18°,求∠A和∠C的度数.∵∠A+∠ABD+∠ADB=180°,∵BD⊥AC,∴∠ADB=∠CDB=90°.∠ABD=54°,∠ADB=90°,∴∠A=180°-∠ABD-∠ADB=180°-54°-90°=36°.解:∠C=180°-∠A-(∠ABD+∠DBC)=180°-36°-(54°+18°)=72°.三角形三角形的概念:由不在同一条直线上的三条线段首尾依次相接所组成的封闭图形.课堂小结三角形按角分类直角三角形锐角三角形钝角三角形三角形的内角和等于180°直角三角形的两个锐角互余
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
