鲁教版数学八年级下册课件9.5相似三角形判定定理的证明 (共13张PPT)
文档属性
| 名称 | 鲁教版数学八年级下册课件9.5相似三角形判定定理的证明 (共13张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 98.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-14 00:00:00 | ||
图片预览





文档简介
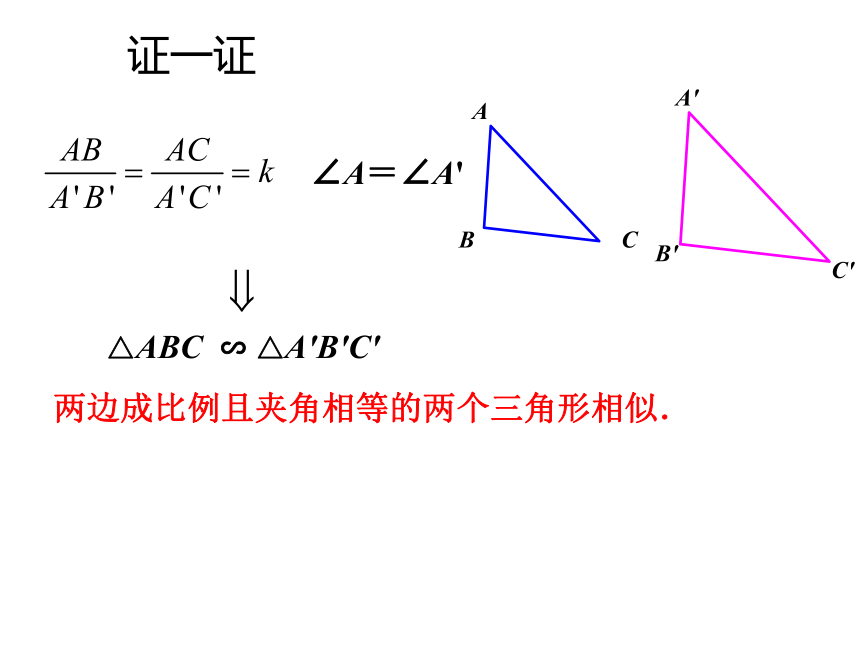
课件13张PPT。9.5 相似三角形判定定理的证明 三角形相似的条件:回顾两边成比例且夹角相等的两个三角形相似.三边对应成比例的两个三角形相似两角分别相等的两个三角形相似.如图,已知△ABC和△A'B'C'中,∠A=∠A', ∠B=∠B',
求证: △ABC∽△A'B'C'证明:在△ABC的边AB(或延长线)上,截取AD=A'B',过点D作DE//BC,交AC于点E,则有△ADE∽△ABC∵∠ADE=∠B, ∠B=∠B',∴∠ADE=∠B'.又∵∠A=∠A',AD=A'B',∴△ADE≌△A'B'C'.∴△A'B'C'∽△ABC.证一证∠A=∠A'△ABC ∽ △A'B'C'两边成比例且夹角相等的两个三角形相似.证一证已知:如图, △A'B'C'和 △ABC中,∠A ' =∠A,A'B':AB=A'C':AC求证:△A'B'C' ∽ △ABC 证明:在△ABC 的边AB、AC(或它们的延长线)上别截取AD=A'B',AE=A'C',连接DE,因∠A ' =∠A,这样△A'B'C' ≌ △ADE ∴ DE//BC.∴ △ADE ∽ △ABC.∴ △A'B'C' ∽ △ABC. A'B'C'ABCDE类似于证明通过两角或两边及夹角判定三角形相似的方法,请你自己证明这个结论.证一证对于△ABC和△A'B'C',如果 ∠B=∠B',这两个三角形一定相似吗?试着画画看. 不 一 定 相 似根据下列条件,判断△ABC与△A'B'C'是否相似,并说明理由:
(1)∠A=120°,AB=7cm,AC=14cm,
∠A'=120°,A'B'=3cm,A'C'=6cm;解:(1)∵又 ∠A=∠A'∴ △ABC∽△A'B'C'例1两三角形的相似比是多少?例题讲解(2)∵要使两三角形相似,不改变AC的长,A'C'的长应当改为多少?△ABC与△A'B'C'的三组对应边的比不等,它们不相似(2)AB=4cm,BC=6cm,AC=8cm.
A'B'=12cm,B'C'=18cm,A'C'=21cm.
1.根据下列条件,判断△ABC与△A'B'C'是否相似,并说明理由:(1)∠A=40°,AB=8,AC=15
∠A' =40°,A'B' =16,A'C' =30
(2)AB=10cm,BC=8cm,AC=16cm
A'B' =16cm,B'C' =12.8cm,A'C' =25.6cm解: (1)∠A=∠A'∴△ABC∽△A'B'C' 练 习∴△ABC∽△A'B'C'(2)2. 图中的两个三角形是否相似?∠ACB=∠ECD∴△ACB∽△ECD对应边的比不相等∴图中两个三角形不相似.解:(1)(2)3.要制作两个形状相同的三角形框架,其中一个三角形框架的三边长分别为4、5、6,另一个三角形框架的一边长为2,它的另外两条边长应当是多少?你有几个答案?方案(1)解:设另外两条边长分别为x , y 练 习方案(3)方案(2) 练 习
求证: △ABC∽△A'B'C'证明:在△ABC的边AB(或延长线)上,截取AD=A'B',过点D作DE//BC,交AC于点E,则有△ADE∽△ABC∵∠ADE=∠B, ∠B=∠B',∴∠ADE=∠B'.又∵∠A=∠A',AD=A'B',∴△ADE≌△A'B'C'.∴△A'B'C'∽△ABC.证一证∠A=∠A'△ABC ∽ △A'B'C'两边成比例且夹角相等的两个三角形相似.证一证已知:如图, △A'B'C'和 △ABC中,∠A ' =∠A,A'B':AB=A'C':AC求证:△A'B'C' ∽ △ABC 证明:在△ABC 的边AB、AC(或它们的延长线)上别截取AD=A'B',AE=A'C',连接DE,因∠A ' =∠A,这样△A'B'C' ≌ △ADE ∴ DE//BC.∴ △ADE ∽ △ABC.∴ △A'B'C' ∽ △ABC. A'B'C'ABCDE类似于证明通过两角或两边及夹角判定三角形相似的方法,请你自己证明这个结论.证一证对于△ABC和△A'B'C',如果 ∠B=∠B',这两个三角形一定相似吗?试着画画看. 不 一 定 相 似根据下列条件,判断△ABC与△A'B'C'是否相似,并说明理由:
(1)∠A=120°,AB=7cm,AC=14cm,
∠A'=120°,A'B'=3cm,A'C'=6cm;解:(1)∵又 ∠A=∠A'∴ △ABC∽△A'B'C'例1两三角形的相似比是多少?例题讲解(2)∵要使两三角形相似,不改变AC的长,A'C'的长应当改为多少?△ABC与△A'B'C'的三组对应边的比不等,它们不相似(2)AB=4cm,BC=6cm,AC=8cm.
A'B'=12cm,B'C'=18cm,A'C'=21cm.
1.根据下列条件,判断△ABC与△A'B'C'是否相似,并说明理由:(1)∠A=40°,AB=8,AC=15
∠A' =40°,A'B' =16,A'C' =30
(2)AB=10cm,BC=8cm,AC=16cm
A'B' =16cm,B'C' =12.8cm,A'C' =25.6cm解: (1)∠A=∠A'∴△ABC∽△A'B'C' 练 习∴△ABC∽△A'B'C'(2)2. 图中的两个三角形是否相似?∠ACB=∠ECD∴△ACB∽△ECD对应边的比不相等∴图中两个三角形不相似.解:(1)(2)3.要制作两个形状相同的三角形框架,其中一个三角形框架的三边长分别为4、5、6,另一个三角形框架的一边长为2,它的另外两条边长应当是多少?你有几个答案?方案(1)解:设另外两条边长分别为x , y 练 习方案(3)方案(2) 练 习
