高中数学(人教)必修4:第一章《 三角函数》单元检测试卷A
文档属性
| 名称 | 高中数学(人教)必修4:第一章《 三角函数》单元检测试卷A |  | |
| 格式 | zip | ||
| 文件大小 | 194.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-14 14:13:07 | ||
图片预览




文档简介
高中数学(人教)必修4:第一章《
三角函数》单元检测试卷A
(测试时间:120分钟 评价分值:150分)
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.sin
120°的值是(
)
A. B.-
C.
D.-
2.把-π表示成θ+2kπ(k∈Z)的形式,使|θ|最小的角θ的值是(
)
A.-
B.-
C.
D.
3.若sin
α>0且tan
α<0,则α是(
)
A.第一象限角
B.第二象限角
C.第三象限角
D.第四象限角
4.集合M=中的元素有(
)
A.无数个
B.4个
C.3个
D.2个
5.如果函数f(x)=sin(πx+θ)(0<θ<2π)的最小正周期为T,且当x=2时,取得最大值,那么(
)
A.T=2,θ=
B.T=1,θ=π
C.T=2,θ=π
D.T=1,θ=
6.已知cos=,且α∈,则tan
α=(
)
A.
B.
C.-
D.±
7.若=2,则tan
α的值为(
)
A.1
B.-1
C.
D.-
8.圆心角为60°的扇形,它的弧长为2π,则它的内切圆的半径为(
)
A.2
B.
C.1
D.
9.使sin
x≤cos
x成立的x的一个区间是(
)
A.
B.
C.
D.[0,π]
10.为了得到函数y=sin(2x+1)的图象,只需把函数y=sin
2x的图象上所有的点(
)
A.向左平行移动个单位长度
B.向右平行移动个单位长度
C.向左平行移动1个单位长度
D.向右平行移动1个单位长度
11.设函数y=sin(2x-1)的最小正周期为T,最大值为A,则(
)
A.T=π,A=1
B.T=2π,A=1
C.T=π,A=2
D.T=2π,A=2
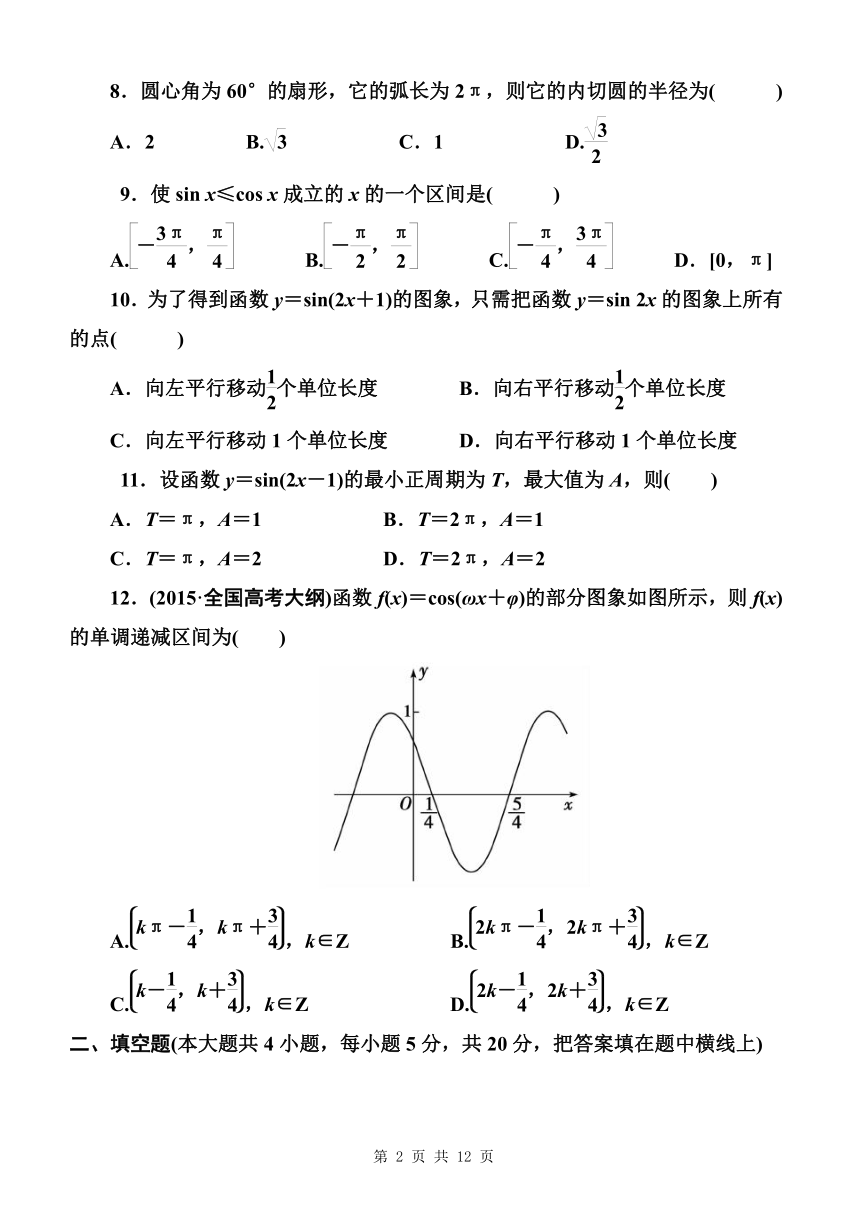
12.(2015·全国高考大纲)函数f(x)=cos(ωx+φ)的部分图象如图所示,则f(x)的单调递减区间为(
)
A.,k∈Z
B.,k∈Z
C.,k∈Z
D.,k∈Z
二、填空题(本大题共4小题,每小题5分,共20分,把答案填在题中横线上)
13.已知α为锐角,且cos=,则sin
α=________.
14.已知角α的终边上一点P与点A(-3,2)关于y轴对称,角β的终边上一点Q与点A关于原点对称,那么sin
α+sin
β的值等于________.
15.函数f(x)=3sin(2x+5θ)的图象关于y轴对称,则θ=________________________.
16.已知函数y=cos
x与函数y=sin(2x+α)(0≤α<π),它们的图象有一个横坐标为的交点,则φ的值是________.
三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分12分)已知α∈,sin
α=.
(1)求sin的值;
(2)求cos的值.
18.(本小题满分12分)已知sin
θ-cos
θ=.
(1)求sin
θ·cos
θ的值;
(2)当0<θ<π时,求tan
θ的值.
19.(本小题满分12分)已知函数y=2acos+b的定义域是,值域是[-5,1],求a、b的值.
20.(本小题满分12分)函数f1(x)=Asin(ωx+φ)的一段图象如下图所示,
(1)求函数f1(x)的解析式;
(2)将函数y=f1(x)的图象向右平移个单位,得函数y=f2(x)的图象,求y=f2(x)的最大值,并求此时自变量x的集合.
21.(本小题满分12分)设函数f(x)=sin(2x+φ)(-π<φ<0),y=f(x)图象的一条对称轴是直线x=.
(1)求φ;
(2)求函数y=f(x)的单调增区间.
22.(本小题满分10分)2013年的元旦,N市从0时到24时的气温变化曲线近似地满足函数y=Asin(ωx+φ)+b(A>0,ω>0,|φ|≤π).从天气台得知:N市在2013年的第一天的温度为1到9度,其中最高气温只出现在下午14时,最低气温只出现在凌晨2时.
(1)求函数y=Asin(ωx+φ)+b的表达式;
(2)若元旦当天M市的气温变化曲线也近似地满足函数y1=A1sin(ω1x+φ1)+b1,且气温变化也为1到9度,只不过最高气温和最低气温出现的时间都比N市迟了4小时.
①求早上7时,N市与M市的两地温差;
②若同一时刻两地的温差不超过2度,我们称之为温度相近,求2013年元旦当日,N市与M市温度相近的时长.
参考答案
一、1.A
2.A
解析:-π=-2π-π,故选A.
3.B
解析:∵sin
α>0,∴α为第一象限角或第二象限角或终边落在y轴非负半轴上,又∵tan
α<0,∴α为第二象限角或第四象限角,∴α为第二象限角.故选B.
4.C
5.A
解析:∵T==2,f(x)=sin(πx+θ),
∴f(2)=sin(2π+θ)=1,θ=.故选A.
6.B
解析:cos=-sin
α=,sin
α=-,
∵α∈,∴cos
α=-,∴tan
α=.故选B.
7.A
8.A
解析:由已知扇形所在圆的半径R==6,设该扇形内切圆半径为r,则6-r=2r,∴r=2,故选A.
9.A
10.A解析:y=sin(2x+1)=sin2,所以只需把y=sin
2x的图象上所有的点向左平移个单位,选A.
11.A
12.D
二、13.答案:
解析:∵α为锐角,∴sin=.∴sin
α=sin=sincos-cossin=×-×=.
14.答案:0
解析:点P的坐标为(3,2),点Q的坐标为(3,-2),∴sin
α==,sin
β==.
∴sin
α+sin
β=0.
15.答案:+(k∈Z)
解析:函数f(x)=3sin(2x+5θ)的图象关于y轴对称,即f(x)在x=0时取得最大值或最小值.由已知得,f(0)=3sin
5θ=±3,即sin
5θ=±1,所以5θ=kπ+(k∈Z),解得θ=+(k∈Z).
16.答案:
解析:由题意cos=sin,即sin=,+φ=kπ+(-1)k,(k∈z),因为0≤φ<π,所以φ=.
三、17.解析:(1)要求sin的值,根据两角和的正弦公式,可知还要求得cos
α,由于已知α∈,所以cos
α<0,利用同角关系可得;
(2)要求cos,由两角差的余弦公式我们知要先求得sin
2α,cos
2α,而这由二倍角公式结合(1)可很容易得到本题应该是三角函数最基本的题型,只要应用公式,不需要作三角函数问题中常见的“角”的变换,“函数名称”的变换等技巧,可以算得上是容易题,当然要正确地解题,也必须牢记公式,及计算正确.
试题解析:(1)由题意cos
α=
-=-,
所以sin=sincos
α+cossin
α=×+×=-.
(2)由(1)得sin
2α=2sin
αcos
α=-,cos
2α=2cos2
α-1=,
所以cos=coscos
2α+sinsin
2α=-×+×=-.
18.解析:(1)(sin
θ-cos
θ)2=1-2sin
θcos
θ== sin
θcos
θ=.
(2)因为0<θ<π且sin
θcos
θ>0,所以
0<θ<.
由
得tan
θ==.
19.解析:∵0≤x≤,∴-≤2x-≤.∴-≤cos≤1.
当a>0时,-a+b≤2acos+b≤2a+b.
由已知得,∴
当a<0时,2a+b≤2acos+b≤-a+b.由已知得,
∴
20.解析:(1)由图象可知,A=2,=-=,∴ω==2.
又∵图象过点,∴2×+φ=kπ(k∈Z).
又∵|φ|<,∴φ=.∴f1(x)=2sin.
(2)∵将函数f1(x)=2sin的图象向右平移个单位,得到函数f2(x)=2sin=2sin的图象.
∵函数f2(x)=2sin的定义域是R,∴函数f2(x)=2sin的最大值是2,
此时2x-=+2kπ,
x=+kπ(k∈Z),∴当函数f2(x)=2sin的最大值是2时,自变量x的集合是.
21.解析:(1)∵x=是函数y=f(x)的图象的对,∴sin=±1,∴+φ=kπ+,k∈Z.
又∵-π<φ<0,∴φ=-.
(2)由(1)知φ=-,因此y=sin.
由题意得2kπ-≤2x-≤2kπ+,k∈Z时,y单调递增.
即kπ+≤x≤kπ+π,k∈Z时,y单调递增.
所以函数y=sin的单调增区间为,k∈Z.
22.解析:由已知可得:b=5,A=4,T=24 ω=.
又最低气温出现在凌晨2时,则有2ω+φ=2kπ-,又|φ|≤π φ=-π.
则所求的函数表达式为y=4sin+5.
(2)由已知得M市的气温变化曲线近似地满足函数y1=4sin+5,y-y1=4
=4
=4sin.
①当x=7时,y-y1=4sin=2.
②由|y-y1|≤2 -2≤4sin≤2 2≤x≤6或14≤x≤18.
则2013年元旦当日,N市与M市温度相近的时长为8小时.
第
1
页
共
8
页
三角函数》单元检测试卷A
(测试时间:120分钟 评价分值:150分)
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.sin
120°的值是(
)
A. B.-
C.
D.-
2.把-π表示成θ+2kπ(k∈Z)的形式,使|θ|最小的角θ的值是(
)
A.-
B.-
C.
D.
3.若sin
α>0且tan
α<0,则α是(
)
A.第一象限角
B.第二象限角
C.第三象限角
D.第四象限角
4.集合M=中的元素有(
)
A.无数个
B.4个
C.3个
D.2个
5.如果函数f(x)=sin(πx+θ)(0<θ<2π)的最小正周期为T,且当x=2时,取得最大值,那么(
)
A.T=2,θ=
B.T=1,θ=π
C.T=2,θ=π
D.T=1,θ=
6.已知cos=,且α∈,则tan
α=(
)
A.
B.
C.-
D.±
7.若=2,则tan
α的值为(
)
A.1
B.-1
C.
D.-
8.圆心角为60°的扇形,它的弧长为2π,则它的内切圆的半径为(
)
A.2
B.
C.1
D.
9.使sin
x≤cos
x成立的x的一个区间是(
)
A.
B.
C.
D.[0,π]
10.为了得到函数y=sin(2x+1)的图象,只需把函数y=sin
2x的图象上所有的点(
)
A.向左平行移动个单位长度
B.向右平行移动个单位长度
C.向左平行移动1个单位长度
D.向右平行移动1个单位长度
11.设函数y=sin(2x-1)的最小正周期为T,最大值为A,则(
)
A.T=π,A=1
B.T=2π,A=1
C.T=π,A=2
D.T=2π,A=2
12.(2015·全国高考大纲)函数f(x)=cos(ωx+φ)的部分图象如图所示,则f(x)的单调递减区间为(
)
A.,k∈Z
B.,k∈Z
C.,k∈Z
D.,k∈Z
二、填空题(本大题共4小题,每小题5分,共20分,把答案填在题中横线上)
13.已知α为锐角,且cos=,则sin
α=________.
14.已知角α的终边上一点P与点A(-3,2)关于y轴对称,角β的终边上一点Q与点A关于原点对称,那么sin
α+sin
β的值等于________.
15.函数f(x)=3sin(2x+5θ)的图象关于y轴对称,则θ=________________________.
16.已知函数y=cos
x与函数y=sin(2x+α)(0≤α<π),它们的图象有一个横坐标为的交点,则φ的值是________.
三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分12分)已知α∈,sin
α=.
(1)求sin的值;
(2)求cos的值.
18.(本小题满分12分)已知sin
θ-cos
θ=.
(1)求sin
θ·cos
θ的值;
(2)当0<θ<π时,求tan
θ的值.
19.(本小题满分12分)已知函数y=2acos+b的定义域是,值域是[-5,1],求a、b的值.
20.(本小题满分12分)函数f1(x)=Asin(ωx+φ)的一段图象如下图所示,
(1)求函数f1(x)的解析式;
(2)将函数y=f1(x)的图象向右平移个单位,得函数y=f2(x)的图象,求y=f2(x)的最大值,并求此时自变量x的集合.
21.(本小题满分12分)设函数f(x)=sin(2x+φ)(-π<φ<0),y=f(x)图象的一条对称轴是直线x=.
(1)求φ;
(2)求函数y=f(x)的单调增区间.
22.(本小题满分10分)2013年的元旦,N市从0时到24时的气温变化曲线近似地满足函数y=Asin(ωx+φ)+b(A>0,ω>0,|φ|≤π).从天气台得知:N市在2013年的第一天的温度为1到9度,其中最高气温只出现在下午14时,最低气温只出现在凌晨2时.
(1)求函数y=Asin(ωx+φ)+b的表达式;
(2)若元旦当天M市的气温变化曲线也近似地满足函数y1=A1sin(ω1x+φ1)+b1,且气温变化也为1到9度,只不过最高气温和最低气温出现的时间都比N市迟了4小时.
①求早上7时,N市与M市的两地温差;
②若同一时刻两地的温差不超过2度,我们称之为温度相近,求2013年元旦当日,N市与M市温度相近的时长.
参考答案
一、1.A
2.A
解析:-π=-2π-π,故选A.
3.B
解析:∵sin
α>0,∴α为第一象限角或第二象限角或终边落在y轴非负半轴上,又∵tan
α<0,∴α为第二象限角或第四象限角,∴α为第二象限角.故选B.
4.C
5.A
解析:∵T==2,f(x)=sin(πx+θ),
∴f(2)=sin(2π+θ)=1,θ=.故选A.
6.B
解析:cos=-sin
α=,sin
α=-,
∵α∈,∴cos
α=-,∴tan
α=.故选B.
7.A
8.A
解析:由已知扇形所在圆的半径R==6,设该扇形内切圆半径为r,则6-r=2r,∴r=2,故选A.
9.A
10.A解析:y=sin(2x+1)=sin2,所以只需把y=sin
2x的图象上所有的点向左平移个单位,选A.
11.A
12.D
二、13.答案:
解析:∵α为锐角,∴sin=.∴sin
α=sin=sincos-cossin=×-×=.
14.答案:0
解析:点P的坐标为(3,2),点Q的坐标为(3,-2),∴sin
α==,sin
β==.
∴sin
α+sin
β=0.
15.答案:+(k∈Z)
解析:函数f(x)=3sin(2x+5θ)的图象关于y轴对称,即f(x)在x=0时取得最大值或最小值.由已知得,f(0)=3sin
5θ=±3,即sin
5θ=±1,所以5θ=kπ+(k∈Z),解得θ=+(k∈Z).
16.答案:
解析:由题意cos=sin,即sin=,+φ=kπ+(-1)k,(k∈z),因为0≤φ<π,所以φ=.
三、17.解析:(1)要求sin的值,根据两角和的正弦公式,可知还要求得cos
α,由于已知α∈,所以cos
α<0,利用同角关系可得;
(2)要求cos,由两角差的余弦公式我们知要先求得sin
2α,cos
2α,而这由二倍角公式结合(1)可很容易得到本题应该是三角函数最基本的题型,只要应用公式,不需要作三角函数问题中常见的“角”的变换,“函数名称”的变换等技巧,可以算得上是容易题,当然要正确地解题,也必须牢记公式,及计算正确.
试题解析:(1)由题意cos
α=
-=-,
所以sin=sincos
α+cossin
α=×+×=-.
(2)由(1)得sin
2α=2sin
αcos
α=-,cos
2α=2cos2
α-1=,
所以cos=coscos
2α+sinsin
2α=-×+×=-.
18.解析:(1)(sin
θ-cos
θ)2=1-2sin
θcos
θ== sin
θcos
θ=.
(2)因为0<θ<π且sin
θcos
θ>0,所以
0<θ<.
由
得tan
θ==.
19.解析:∵0≤x≤,∴-≤2x-≤.∴-≤cos≤1.
当a>0时,-a+b≤2acos+b≤2a+b.
由已知得,∴
当a<0时,2a+b≤2acos+b≤-a+b.由已知得,
∴
20.解析:(1)由图象可知,A=2,=-=,∴ω==2.
又∵图象过点,∴2×+φ=kπ(k∈Z).
又∵|φ|<,∴φ=.∴f1(x)=2sin.
(2)∵将函数f1(x)=2sin的图象向右平移个单位,得到函数f2(x)=2sin=2sin的图象.
∵函数f2(x)=2sin的定义域是R,∴函数f2(x)=2sin的最大值是2,
此时2x-=+2kπ,
x=+kπ(k∈Z),∴当函数f2(x)=2sin的最大值是2时,自变量x的集合是.
21.解析:(1)∵x=是函数y=f(x)的图象的对,∴sin=±1,∴+φ=kπ+,k∈Z.
又∵-π<φ<0,∴φ=-.
(2)由(1)知φ=-,因此y=sin.
由题意得2kπ-≤2x-≤2kπ+,k∈Z时,y单调递增.
即kπ+≤x≤kπ+π,k∈Z时,y单调递增.
所以函数y=sin的单调增区间为,k∈Z.
22.解析:由已知可得:b=5,A=4,T=24 ω=.
又最低气温出现在凌晨2时,则有2ω+φ=2kπ-,又|φ|≤π φ=-π.
则所求的函数表达式为y=4sin+5.
(2)由已知得M市的气温变化曲线近似地满足函数y1=4sin+5,y-y1=4
=4
=4sin.
①当x=7时,y-y1=4sin=2.
②由|y-y1|≤2 -2≤4sin≤2 2≤x≤6或14≤x≤18.
则2013年元旦当日,N市与M市温度相近的时长为8小时.
第
1
页
共
8
页
