第八章平行线的有关证明 检测题含答案
图片预览

文档简介
第八章
平行线的有关证明
检测题
一、精心选一选(每小题3分,共30分)
1.
如图1,已知直线a,b被直线c所截,且a∥b,则得到∠1=∠2的依据是(
)
A.
两直线平行,同位角相等
B.
同位角相等,两直线平行
C.
两直线平行,内错角相等
D.
内错角相等,两直线平行
2.
下列命题中,是真命题的是(
)
A.
点(1,2)在x轴上
B.
三角形的内角和等于360
C.
无理数不是实数
D.
同旁内角互补,两直线平行
3.
如图2,下列条件能判定EC∥AB的是(
)
A.
∠B=∠ACE
B.
∠A=∠ECD
C.
∠B=∠ACB
D.
∠A=∠ACE
4.
(2015年滨州)在△ABC中,∠A︰∠B︰∠C=3︰4︰5,则∠C的度数是(
)
A.
45
B.
60
C.
75
D.
90
5.
如图3,直线a,b,c,d互不平行,对它们截出的一些角的数量关系描述正确的是(
)
A.
∠1<180 -(∠4+∠5)
B.
∠2=∠4+∠5
C.
∠2<∠3
D.
∠1>∠6
6.(2015年南昌)如图4,已知AB∥CD,FE⊥DB,垂足为E,∠1=50 ,则∠2的度数为(
)
A.
60
B.
50
C.
40
D.
30
7.
命题“同角的余角相等”改写成“如果……,那么……”的形式是(
)
A.
如果是同角的余角,那么相等
B.
如果两个角是同一个角的余角,那么这两个角相等
C.
如果两个角是同角,那么这两个角是余角
D.
如果两个角互余,那么这两个角相等
8.(2015年滨州)如图5,直线AC∥BD,AO,BO分别是∠BAC,∠ABD的平分线,那么∠BAO与∠ABO之间关系一定是(
)
A.
互余
B.
相等
C.
互补
D.
不等
9.
甲、乙、丙三位先生是同一家公司的职员,他们的夫人M,N,P也都是这家公司的职员,知情者介绍:M的丈夫是乙的好友,且在三位先生中最年轻,丙的年龄比P的丈夫大.
根据知情者提供的信息,可以推出三对夫妇分别是(
)
A.
甲和M,乙和N,丙和P
B.
甲和M,乙和P,丙和N
C.
甲和N,乙和P,丙和M
D.
甲和P,乙和N,丙和M
10.
如图6,C是∠BAD内一点,连接BC,CD,∠BAD的平分线AE与∠BCD的平分线CE交于点E,延长BC交AD于点F.已知∠D=20 ,∠B=40 ,则∠E的度数是(
)
A.10
B.12
C.14
D.16
二、细心填一填(每小题3分,共24分)
11.
如图7,要判断AB∥CD,需要增加的条件是________________.
12.
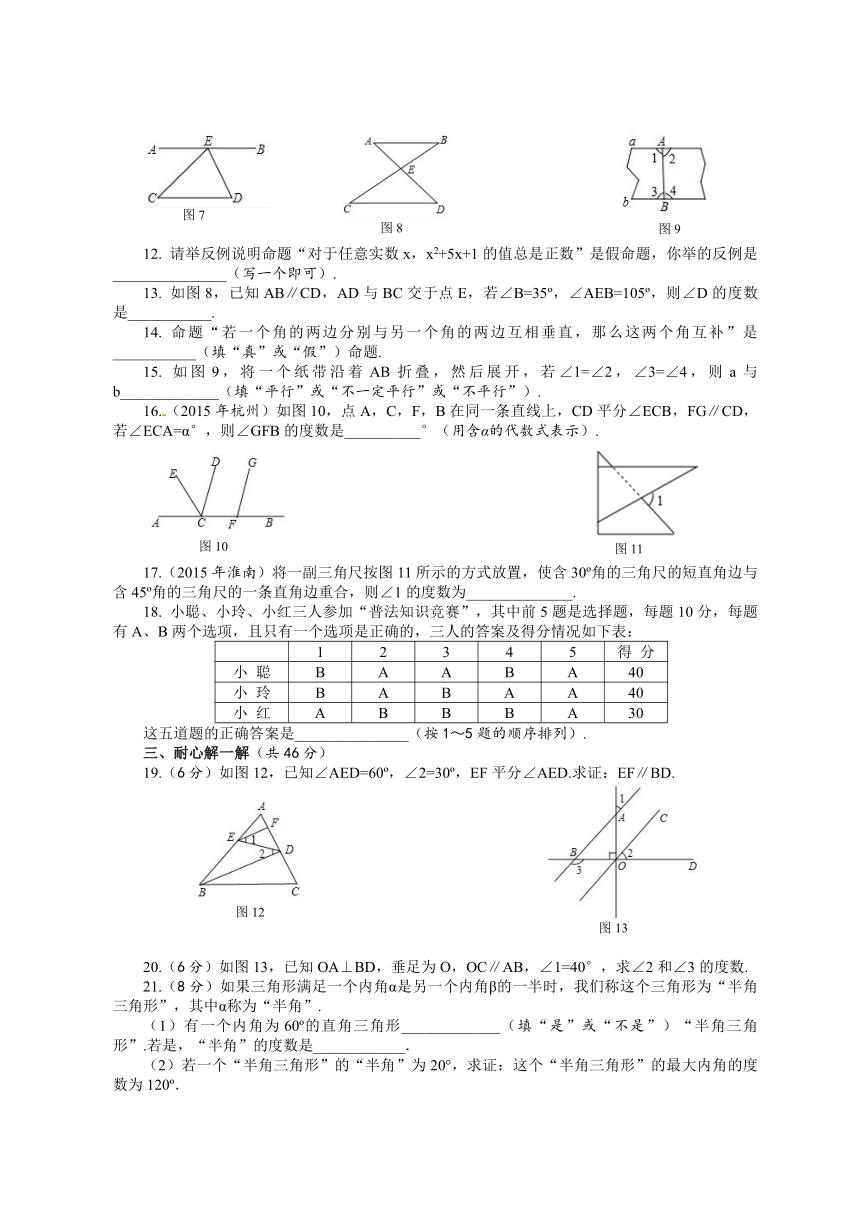
请举反例说明命题“对于任意实数x,x2+5x+1的值总是正数”是假命题,你举的反例是_______________(写一个即可).
13.
如图8,已知AB∥CD,AD与BC交于点E,若∠B=35 ,∠AEB=105 ,则∠D的度数是___________.
14.
命题“若一个角的两边分别与另一个角的两边互相垂直,那么这两个角互补”是___________(填“真”或“假”)命题.
15.
如图9,将一个纸带沿着AB折叠,然后展开,若∠1=∠2,∠3=∠4,则a与b_____________(填“平行”或“不一定平行”或“不平行”).
16.(2015年杭州)如图10,点A,C,F,B在同一条直线上,CD平分∠ECB,FG∥CD,若∠ECA=α°,则∠GFB的度数是__________°(用含α的代数式表示).
17.(2015年淮南)将一副三角尺按图11所示的方式放置,使含30 角的三角尺的短直角边与含45 角的三角尺的一条直角边重合,则∠1的度数为______________.
18.
小聪、小玲、小红三人参加“普法知识竞赛”,其中前5题是选择题,每题10分,每题有A、B两个选项,且只有一个选项是正确的,三人的答案及得分情况如下表:
1
2
3
4
5
得
分
小
聪
B
A
A
B
A
40
小
玲
B
A
B
A
A
40
小
红
A
B
B
B
A
30
这五道题的正确答案是_______________(按1~5题的顺序排列).
三、耐心解一解(共46分)
19.(6分)如图12,已知∠AED=60 ,∠2=30 ,EF平分∠AED.求证:EF∥BD.
20.(6分)如图13,已知OA⊥BD,垂足为O,OC∥AB,∠1=40°,求∠2和∠3的度数.
21.(8分)如果三角形满足一个内角α是另一个内角β的一半时,我们称这个三角形为“半角三角形”,其中α称为“半角”.
(1)有一个内角为60 的直角三角形_____________(填“是”或“不是”)“半角三角形”.若是,“半角”的度数是____________.
(2)若一个“半角三角形”的“半角”为20°,求证:这个“半角三角形”的最大内角的度数为120 .
22.(8分)如图14,在△ABC中,D是AC上一点,连接BD,E是BD上一点,连接CE,已知∠A=60 ,给出如下关系:①∠1+∠3-∠2=60 ;②∠2-∠1-∠3=60 ;③∠1+∠2-∠3=60 .
请选择正确结论的序号,并证明你的结论.
23.(8分)问题情境:如图15,已知AB∥CD,∠1=∠2,求证:∠3=∠4.
解法展示:证明:延长BE交直线CD于点M,如图16所示.
∵AB∥CD,∴∠1=∠BMC(根据1).
∵∠1=∠2,
∴∠2=∠BMC(根据2).
∴BE∥CF(根据3).
∴∠3=∠4(根据4).
反思交流:(1)解法展示中的根据1是______________,根据2是______________,根据3是________________,根据4是________________.
(2)上述命题中,条件记为:①AB∥CD,②∠1=∠2,结论记为:③∠3=∠4.
若把其中的一个条件和结论对调,得到一个新命题,写出这个命题(用序号表示即可),判断新命题的真假,并说明理由.
24.(10分)给出如下命题:“邻补角的平分线互相垂直”.
(1)把这个命题写成“如果……,那么……”的形式;
(2)判断这个命题是真命题还是假命题?若是真命题,写出已知、求证、画出图形,并写出证明过程;若是假命题,举反例说明.
附加题(共20分)
25.(10分)(2015年台湾)大冠买了一包宣纸练习书法,每星期一写1张,每星期二写2张,每星期三写3张,每星期四写4张,每星期五写5张,每星期六写6张,每星期日写7张.若大冠从某年的5月1日开始练习,到5月30日练习完后积累写完的宣纸总数已超过120张,则5月30日可能为星期几?请求出所有可能的答案,并完整说明理由.
26.(10分)如图17—①,△ABC的顶点B,C分别在△DEF的两边DE,DF上,∠A=50 ,∠E+∠F=100 .
(1)求∠ABD+∠ACD的度数;
(2)若将△DEF的位置由图17-①变为图17-②,其他条件不变,求∠ABD+∠ACD的度数;
(3)在图17-②中,是否存在BD和CD同时平分∠ABC和∠ACB?(不必说明理由)
参考答案
一、1.
A
2.
D
3.
D
4.
C
5.
B
6.
C
7.
B
8.
A
9.
B
提示:因为M的丈夫是乙的好友,并在三位先生中最年轻,所以M的丈夫一定不是乙,可能是甲或丙.
因为丙的年龄比P的丈夫大,所以P与丙一定不是夫妻,且M的丈夫一定是甲.所以P的丈夫是乙,N的丈夫是丙.
10.
A
提示:因为∠BFD=∠BAF+∠B,所以∠BCD=∠BFD+∠D=∠BAF+40 +20 =∠BAF+60 .
因为CE平分∠BCD,AE平分∠BAD,所以∠ECB=∠BCD=∠BAF+30 ,∠EAB=∠BAF.因为∠E+∠ECB=∠B+∠EAB,所以∠E+∠BAF+30 =40 +∠BAF.所以∠E=10 .
二、11.
答案不唯一,如∠AEC=∠C
12.
答案不唯一,如x=-1
13.
40
14.
假
15.
平行
16.(90-)
17.
75
18.
BABBA
提示:由得分,知小聪和小玲都是错了1道题,小红错了2道题.因为小聪和小玲第3题和第4题答案不一样,所以这两道题中一人错了一道,故第1,2,5题的答案可以确定分别为BAA.所以小红的第1,2题是错误的,第3,4题的答案是正确的,分别为BB.
三、19.
证明:∵EF平分∠AED,∴∠1=∠AED.
∵∠AED=60 ,∴∠1=×60 =30 .∵∠2=30 ,∴∠1=∠2.∴EF∥BD.
20.
证明:∵OC∥AB,∴∠1=∠AOC.
∵OA⊥BD,∴∠AOC+∠2=90 .∴∠2=90 -40°=50°.
∵∠3是△ABO的一个外角,∴∠3=∠BAO+90 .
又∠BAO=∠1,∴∠3=40°+90 =130°.
21.
解:(1)是
30
(2)由一个“半角三角形”的“半角”为20°,得它的另一个内角为20 ×2=40 .则第三个内角为180 -20 -40 =120 ,即这个“半角三角形”的最大内角的度数为120 .
22.
解:结论正确的是②.
证明:∵∠2是△DEC的一个外角,∴∠2=∠3+∠CDE.
∵∠CDE是△ABD的一个外角,∴∠CDE=∠1+∠A.∴∠2=∠3+∠1+∠A.
∴∠2=∠3+∠1+60 ,即∠2-∠1-∠3=60 .
23.
解:(1)两直线平行,内错角相等
等量代换
同位角相等,两直线平行
两直线平行,内错角相等
(2)交换①和③或交换②和③都是真命题.选择交换②和③,成为新命题.
已知:①③,求证:②.
理由:延长BE交直线CD于点M(同解法展示图).
∵∠3=∠4,∴BE∥CF.∴∠2=∠BMC.
∵AB∥CD,∴∠1=∠BMC.∴∠1=∠2.
24.
解:(1)如果两个角是邻补角,那么这两个角的平分线互相垂直.
(2)这个命题是真命题.
已知:如图,AB,CD相交于点O,OE,OF分别平分∠AOC,∠AOD,求证:OE⊥OF.
证明:因为OE,OF分别平分∠AOC,∠AOD,所以∠AOE=∠AOC,∠AOF=∠AOD.
因为∠AOC+∠AOD=180 ,所以∠AOE+∠AOF=∠AOC+∠AOD=(∠AOC+∠AOD)=×180 =90 .所以OE⊥OF.
25.
解:因为5月1日~30日共30天,包括四个完整的星期,所以5月1日~28日写的张数为.
若5月30日为星期一,所写张数为112+7+1=120;若5月30日为星期二,所写张数为112+1+2<120;若5月30日为星期三,所写张数为112+2+3<120;若5月30日为星期四,所写张数为112+3+4<120;若5月30日为星期五,所写张数为112+4+5>120;若5月30日为星期六,所写张数为112+5+6>120;若5月30日为星期日,所写张数为112+6+7>120.
故5月30日可能是星期五、星期六或星期日.
26.
解:(1)因为∠A+∠ABC+∠ACB=180 ,∠A=50 ,所以∠ABC+∠ACB=180 -50 =130 .
因为∠D+∠DBC+∠DCB=180 ,∠D+∠E+∠F=180 ,所以∠DBC+∠DCB=∠E+∠F
=100 .
所以∠ABD+∠ACD=∠ABC+∠ACB+∠DBC+∠DCB=130 +100 =230 .
(2)因为∠A+∠ABC+∠ACB=180 ,∠A=50 ,所以∠ABC+∠ACB=180 -50 =130 .
因为∠D+∠DBC+∠DCB=180 ,∠D+∠E+∠F=180 ,所以∠DBC+∠DCB=∠E+∠F
=100 .
所以∠ABD+∠ACD=∠ABC+∠ACB-(∠DBC+∠DCB)=130 -100 =30 .
(3)不存在.
图1
1
a
b
c
2
图3
图2
图5
图4
图6
F
图9
图8
图7
图11
图10
图13
图12
图14
1
3
2
图15
图16
A
B
A
F
E
D
C
B
F
E
D
C
①
②
图17
图3
平行线的有关证明
检测题
一、精心选一选(每小题3分,共30分)
1.
如图1,已知直线a,b被直线c所截,且a∥b,则得到∠1=∠2的依据是(
)
A.
两直线平行,同位角相等
B.
同位角相等,两直线平行
C.
两直线平行,内错角相等
D.
内错角相等,两直线平行
2.
下列命题中,是真命题的是(
)
A.
点(1,2)在x轴上
B.
三角形的内角和等于360
C.
无理数不是实数
D.
同旁内角互补,两直线平行
3.
如图2,下列条件能判定EC∥AB的是(
)
A.
∠B=∠ACE
B.
∠A=∠ECD
C.
∠B=∠ACB
D.
∠A=∠ACE
4.
(2015年滨州)在△ABC中,∠A︰∠B︰∠C=3︰4︰5,则∠C的度数是(
)
A.
45
B.
60
C.
75
D.
90
5.
如图3,直线a,b,c,d互不平行,对它们截出的一些角的数量关系描述正确的是(
)
A.
∠1<180 -(∠4+∠5)
B.
∠2=∠4+∠5
C.
∠2<∠3
D.
∠1>∠6
6.(2015年南昌)如图4,已知AB∥CD,FE⊥DB,垂足为E,∠1=50 ,则∠2的度数为(
)
A.
60
B.
50
C.
40
D.
30
7.
命题“同角的余角相等”改写成“如果……,那么……”的形式是(
)
A.
如果是同角的余角,那么相等
B.
如果两个角是同一个角的余角,那么这两个角相等
C.
如果两个角是同角,那么这两个角是余角
D.
如果两个角互余,那么这两个角相等
8.(2015年滨州)如图5,直线AC∥BD,AO,BO分别是∠BAC,∠ABD的平分线,那么∠BAO与∠ABO之间关系一定是(
)
A.
互余
B.
相等
C.
互补
D.
不等
9.
甲、乙、丙三位先生是同一家公司的职员,他们的夫人M,N,P也都是这家公司的职员,知情者介绍:M的丈夫是乙的好友,且在三位先生中最年轻,丙的年龄比P的丈夫大.
根据知情者提供的信息,可以推出三对夫妇分别是(
)
A.
甲和M,乙和N,丙和P
B.
甲和M,乙和P,丙和N
C.
甲和N,乙和P,丙和M
D.
甲和P,乙和N,丙和M
10.
如图6,C是∠BAD内一点,连接BC,CD,∠BAD的平分线AE与∠BCD的平分线CE交于点E,延长BC交AD于点F.已知∠D=20 ,∠B=40 ,则∠E的度数是(
)
A.10
B.12
C.14
D.16
二、细心填一填(每小题3分,共24分)
11.
如图7,要判断AB∥CD,需要增加的条件是________________.
12.
请举反例说明命题“对于任意实数x,x2+5x+1的值总是正数”是假命题,你举的反例是_______________(写一个即可).
13.
如图8,已知AB∥CD,AD与BC交于点E,若∠B=35 ,∠AEB=105 ,则∠D的度数是___________.
14.
命题“若一个角的两边分别与另一个角的两边互相垂直,那么这两个角互补”是___________(填“真”或“假”)命题.
15.
如图9,将一个纸带沿着AB折叠,然后展开,若∠1=∠2,∠3=∠4,则a与b_____________(填“平行”或“不一定平行”或“不平行”).
16.(2015年杭州)如图10,点A,C,F,B在同一条直线上,CD平分∠ECB,FG∥CD,若∠ECA=α°,则∠GFB的度数是__________°(用含α的代数式表示).
17.(2015年淮南)将一副三角尺按图11所示的方式放置,使含30 角的三角尺的短直角边与含45 角的三角尺的一条直角边重合,则∠1的度数为______________.
18.
小聪、小玲、小红三人参加“普法知识竞赛”,其中前5题是选择题,每题10分,每题有A、B两个选项,且只有一个选项是正确的,三人的答案及得分情况如下表:
1
2
3
4
5
得
分
小
聪
B
A
A
B
A
40
小
玲
B
A
B
A
A
40
小
红
A
B
B
B
A
30
这五道题的正确答案是_______________(按1~5题的顺序排列).
三、耐心解一解(共46分)
19.(6分)如图12,已知∠AED=60 ,∠2=30 ,EF平分∠AED.求证:EF∥BD.
20.(6分)如图13,已知OA⊥BD,垂足为O,OC∥AB,∠1=40°,求∠2和∠3的度数.
21.(8分)如果三角形满足一个内角α是另一个内角β的一半时,我们称这个三角形为“半角三角形”,其中α称为“半角”.
(1)有一个内角为60 的直角三角形_____________(填“是”或“不是”)“半角三角形”.若是,“半角”的度数是____________.
(2)若一个“半角三角形”的“半角”为20°,求证:这个“半角三角形”的最大内角的度数为120 .
22.(8分)如图14,在△ABC中,D是AC上一点,连接BD,E是BD上一点,连接CE,已知∠A=60 ,给出如下关系:①∠1+∠3-∠2=60 ;②∠2-∠1-∠3=60 ;③∠1+∠2-∠3=60 .
请选择正确结论的序号,并证明你的结论.
23.(8分)问题情境:如图15,已知AB∥CD,∠1=∠2,求证:∠3=∠4.
解法展示:证明:延长BE交直线CD于点M,如图16所示.
∵AB∥CD,∴∠1=∠BMC(根据1).
∵∠1=∠2,
∴∠2=∠BMC(根据2).
∴BE∥CF(根据3).
∴∠3=∠4(根据4).
反思交流:(1)解法展示中的根据1是______________,根据2是______________,根据3是________________,根据4是________________.
(2)上述命题中,条件记为:①AB∥CD,②∠1=∠2,结论记为:③∠3=∠4.
若把其中的一个条件和结论对调,得到一个新命题,写出这个命题(用序号表示即可),判断新命题的真假,并说明理由.
24.(10分)给出如下命题:“邻补角的平分线互相垂直”.
(1)把这个命题写成“如果……,那么……”的形式;
(2)判断这个命题是真命题还是假命题?若是真命题,写出已知、求证、画出图形,并写出证明过程;若是假命题,举反例说明.
附加题(共20分)
25.(10分)(2015年台湾)大冠买了一包宣纸练习书法,每星期一写1张,每星期二写2张,每星期三写3张,每星期四写4张,每星期五写5张,每星期六写6张,每星期日写7张.若大冠从某年的5月1日开始练习,到5月30日练习完后积累写完的宣纸总数已超过120张,则5月30日可能为星期几?请求出所有可能的答案,并完整说明理由.
26.(10分)如图17—①,△ABC的顶点B,C分别在△DEF的两边DE,DF上,∠A=50 ,∠E+∠F=100 .
(1)求∠ABD+∠ACD的度数;
(2)若将△DEF的位置由图17-①变为图17-②,其他条件不变,求∠ABD+∠ACD的度数;
(3)在图17-②中,是否存在BD和CD同时平分∠ABC和∠ACB?(不必说明理由)
参考答案
一、1.
A
2.
D
3.
D
4.
C
5.
B
6.
C
7.
B
8.
A
9.
B
提示:因为M的丈夫是乙的好友,并在三位先生中最年轻,所以M的丈夫一定不是乙,可能是甲或丙.
因为丙的年龄比P的丈夫大,所以P与丙一定不是夫妻,且M的丈夫一定是甲.所以P的丈夫是乙,N的丈夫是丙.
10.
A
提示:因为∠BFD=∠BAF+∠B,所以∠BCD=∠BFD+∠D=∠BAF+40 +20 =∠BAF+60 .
因为CE平分∠BCD,AE平分∠BAD,所以∠ECB=∠BCD=∠BAF+30 ,∠EAB=∠BAF.因为∠E+∠ECB=∠B+∠EAB,所以∠E+∠BAF+30 =40 +∠BAF.所以∠E=10 .
二、11.
答案不唯一,如∠AEC=∠C
12.
答案不唯一,如x=-1
13.
40
14.
假
15.
平行
16.(90-)
17.
75
18.
BABBA
提示:由得分,知小聪和小玲都是错了1道题,小红错了2道题.因为小聪和小玲第3题和第4题答案不一样,所以这两道题中一人错了一道,故第1,2,5题的答案可以确定分别为BAA.所以小红的第1,2题是错误的,第3,4题的答案是正确的,分别为BB.
三、19.
证明:∵EF平分∠AED,∴∠1=∠AED.
∵∠AED=60 ,∴∠1=×60 =30 .∵∠2=30 ,∴∠1=∠2.∴EF∥BD.
20.
证明:∵OC∥AB,∴∠1=∠AOC.
∵OA⊥BD,∴∠AOC+∠2=90 .∴∠2=90 -40°=50°.
∵∠3是△ABO的一个外角,∴∠3=∠BAO+90 .
又∠BAO=∠1,∴∠3=40°+90 =130°.
21.
解:(1)是
30
(2)由一个“半角三角形”的“半角”为20°,得它的另一个内角为20 ×2=40 .则第三个内角为180 -20 -40 =120 ,即这个“半角三角形”的最大内角的度数为120 .
22.
解:结论正确的是②.
证明:∵∠2是△DEC的一个外角,∴∠2=∠3+∠CDE.
∵∠CDE是△ABD的一个外角,∴∠CDE=∠1+∠A.∴∠2=∠3+∠1+∠A.
∴∠2=∠3+∠1+60 ,即∠2-∠1-∠3=60 .
23.
解:(1)两直线平行,内错角相等
等量代换
同位角相等,两直线平行
两直线平行,内错角相等
(2)交换①和③或交换②和③都是真命题.选择交换②和③,成为新命题.
已知:①③,求证:②.
理由:延长BE交直线CD于点M(同解法展示图).
∵∠3=∠4,∴BE∥CF.∴∠2=∠BMC.
∵AB∥CD,∴∠1=∠BMC.∴∠1=∠2.
24.
解:(1)如果两个角是邻补角,那么这两个角的平分线互相垂直.
(2)这个命题是真命题.
已知:如图,AB,CD相交于点O,OE,OF分别平分∠AOC,∠AOD,求证:OE⊥OF.
证明:因为OE,OF分别平分∠AOC,∠AOD,所以∠AOE=∠AOC,∠AOF=∠AOD.
因为∠AOC+∠AOD=180 ,所以∠AOE+∠AOF=∠AOC+∠AOD=(∠AOC+∠AOD)=×180 =90 .所以OE⊥OF.
25.
解:因为5月1日~30日共30天,包括四个完整的星期,所以5月1日~28日写的张数为.
若5月30日为星期一,所写张数为112+7+1=120;若5月30日为星期二,所写张数为112+1+2<120;若5月30日为星期三,所写张数为112+2+3<120;若5月30日为星期四,所写张数为112+3+4<120;若5月30日为星期五,所写张数为112+4+5>120;若5月30日为星期六,所写张数为112+5+6>120;若5月30日为星期日,所写张数为112+6+7>120.
故5月30日可能是星期五、星期六或星期日.
26.
解:(1)因为∠A+∠ABC+∠ACB=180 ,∠A=50 ,所以∠ABC+∠ACB=180 -50 =130 .
因为∠D+∠DBC+∠DCB=180 ,∠D+∠E+∠F=180 ,所以∠DBC+∠DCB=∠E+∠F
=100 .
所以∠ABD+∠ACD=∠ABC+∠ACB+∠DBC+∠DCB=130 +100 =230 .
(2)因为∠A+∠ABC+∠ACB=180 ,∠A=50 ,所以∠ABC+∠ACB=180 -50 =130 .
因为∠D+∠DBC+∠DCB=180 ,∠D+∠E+∠F=180 ,所以∠DBC+∠DCB=∠E+∠F
=100 .
所以∠ABD+∠ACD=∠ABC+∠ACB-(∠DBC+∠DCB)=130 -100 =30 .
(3)不存在.
图1
1
a
b
c
2
图3
图2
图5
图4
图6
F
图9
图8
图7
图11
图10
图13
图12
图14
1
3
2
图15
图16
A
B
A
F
E
D
C
B
F
E
D
C
①
②
图17
图3
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
