第六章特殊平行四边形 测试题含答案
图片预览

文档简介
第六章
特殊平行四边形
测试题
一、选择题(每小题3分,共30分)
1.
矩形、菱形、正方形都具有的性质是(
)
A.每一条对角线平分一组对角
B.对角线相等
C.对角线互相平分
D.对角线互相垂直
2.小刚和小东在做一道习题,若四边形ABCD是平行四边形,请补充条件,使得四边形ABCD是矩形.小刚补充的条件是:∠A=∠B;小东补充的条件是:∠A+∠C=180°.你认为下列说法正确的是(
)
A.小刚和小东都正确
B.仅小刚正确
C.仅小东正确
D.小刚和小东都错误
3.
(2015年玉林、防城港)如图1,在□ABCD中,BM平分∠ABC,交CD于点M,且MC=2,□ABCD的周长是14,则DM的长为(
)
A.1
B.2
C.3
D.4
4.
(2015年徐州)如图2,在菱形ABCD中,对角线AC,BD交于点O,E为边AD的中点,菱形ABCD的周长为28,则OE的长为(
)
A.3.5
B.4
C.7
D.14
5.
(2015年日照)小明在学习了正方形之后,给同桌小文出了道题.从下列四个条件:①AB=BC;②∠ABC=90°;③AC=BD;④AC⊥BD中选两个作为补充条件,使□ABCD成为正方形(如图3).现有下列四种选法,你认为其中错误的是(
)
A.①②
B.②③
C.①③
D.②④
6.
(2015年安顺)如图4,点O是矩形ABCD对角线的交点,E是AB上的点,折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为(
)
A.2
B.
C.
D.6
7.
如图5,在菱形ABCD中,M,N分别在AB,CD上,且AM=CN,MN与AC交于点O,连接BO.若∠DAC=28°,则∠OBC的度数为(
)
A.28°
B.52°
C.62°
D.72°
8.
如图6,在△ABC中,BD,CE是△ABC的中线,BD与CE相交于点O,点F,G分别是BO,CO的中点,连接AO.若AO=6
cm,BC=8
cm,则四边形DEFG的周长是(
)
A.14
cm
B.18
cm
C.24
cm
D.28
cm
9.
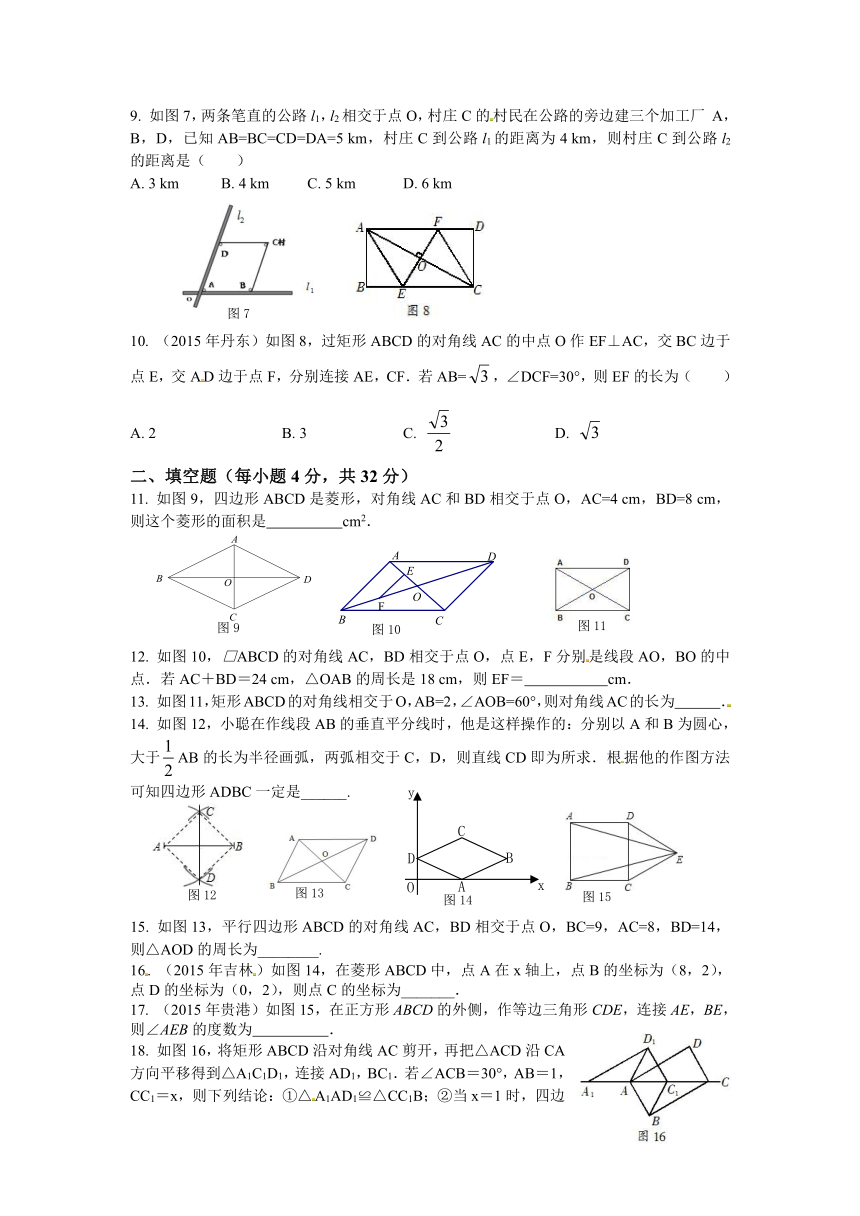
如图7,两条笔直的公路l1,l2相交于点O,村庄C的村民在公路的旁边建三个加工厂
A,B,D,已知AB=BC=CD=DA=5
km,村庄C到公路l1的距离为4
km,则村庄C到公路l2的距离是(
)
A.
3
km
B.
4
km
C.
5
km
D.
6
km
10.
(2015年丹东)如图8,过矩形ABCD的对角线AC的中点O作EF⊥AC,交BC边于点E,交AD边于点F,分别连接AE,CF.若AB=,∠DCF=30°,则EF的长为( )
A.
2
B.
3
C.
D.
二、填空题(每小题4分,共32分)
11.
如图9,四边形ABCD是菱形,对角线AC和BD相交于点O,AC=4
cm,BD=8
cm,则这个菱形的面积是
cm2.
12.
如图10,□ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点.若AC+BD=24
cm,△OAB的周长是18
cm,则EF=
cm.
13.
如图11,矩形ABCD的对角线相交于O,AB=2,∠AOB=60°,则对角线AC的长为
.
14.
如图12,小聪在作线段AB的垂直平分线时,他是这样操作的:分别以A和B为圆心,大于AB的长为半径画弧,两弧相交于C,D,则直线CD即为所求.根据他的作图方法可知四边形ADBC一定是______.
15.
如图13,平行四边形ABCD的对角线AC,BD相交于点O,BC=9,AC=8,BD=14,则△AOD的周长为________.
16.
(2015年吉林)如图14,在菱形ABCD中,点A在x轴上,点B的坐标为(8,2),点D的坐标为(0,2),则点C的坐标为_______.
17.
(2015年贵港)如图15,在正方形ABCD的外侧,作等边三角形CDE,连接AE,BE,则∠AEB的度数为
.
18.
如图16,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连接AD1,BC1.若∠ACB=30°,AB=1,CC1=x,则下列结论:①△A1AD1≌△CC1B;②当x=1时,四边形ABC1D1是菱形;③当x=2时,△BDD1为等边三角形.其中正确的是
.(填序号)
三、解答题(共58分)
19.
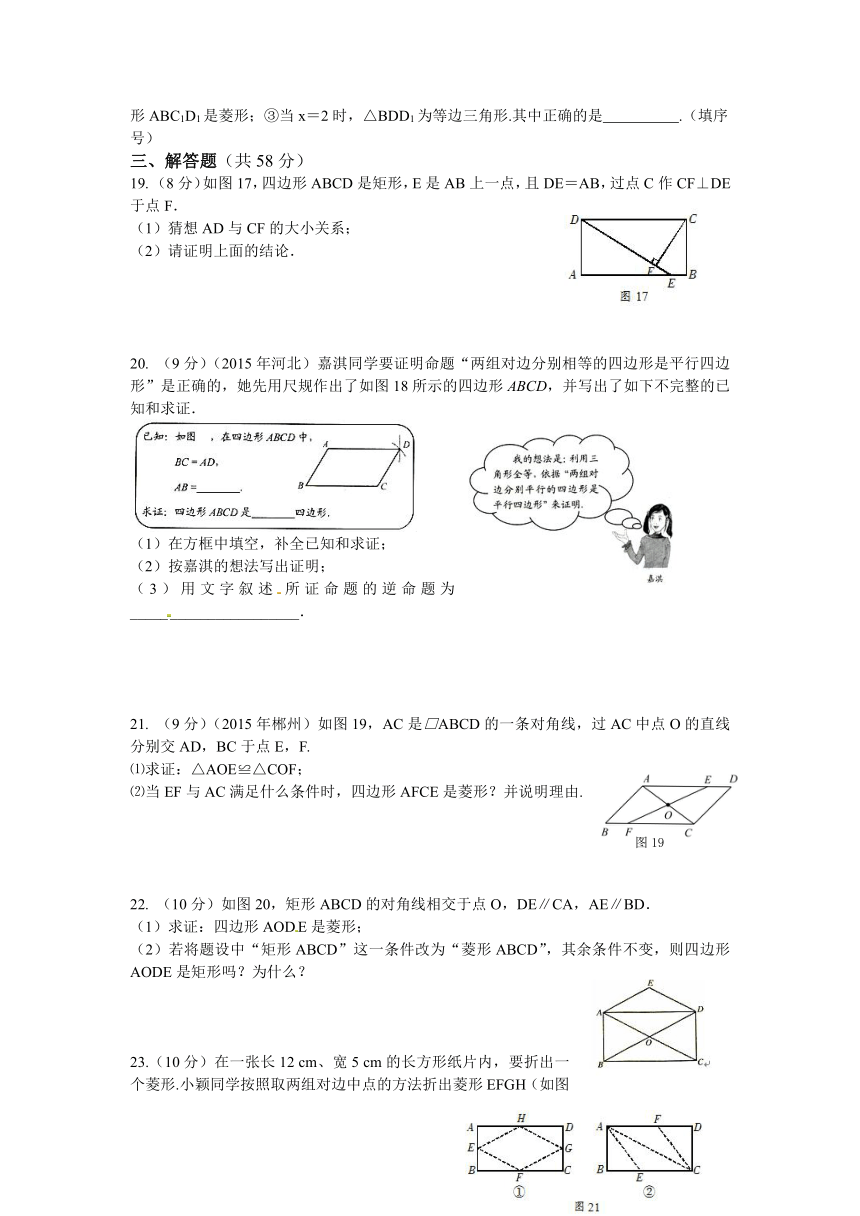
(8分)如图17,四边形ABCD是矩形,E是AB上一点,且DE=AB,过点C作CF⊥DE于点F.
(1)猜想AD与CF的大小关系;
(2)请证明上面的结论.
20.
(9分)(2015年河北)嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图18所示的四边形ABCD,并写出了如下不完整的已知和求证.
(1)在方框中填空,补全已知和求证;
(2)按嘉淇的想法写出证明;
(3)用文字叙述所证命题的逆命题为______________________.
21.
(9分)(2015年郴州)如图19,AC是□ABCD的一条对角线,过AC中点O的直线分别交AD,BC于点E,F.
⑴求证:△AOE≌△COF;
⑵当EF与AC满足什么条件时,四边形AFCE是菱形?并说明理由.
22.
(10分)如图20,矩形ABCD的对角线相交于点O,DE∥CA,AE∥BD.
(1)求证:四边形AODE是菱形;
(2)若将题设中“矩形ABCD”这一条件改为“菱形ABCD”,其余条件不变,则四边形AODE是矩形吗?为什么?
23.(10分)在一张长12
cm、宽5
cm的长方形纸片内,要折出一个菱形.小颖同学按照取两组对边中点的方法折出菱形EFGH(如图21-①),小明同学沿长方形的对角线AC折出∠CAE=∠CAD,∠ACF=∠ACB的方法得到菱形AECF(如图21-②).请问小颖和小明同学的折法中,哪个菱形面积较大?
24.
(12分)如图22-①,在正方形ABCD中,E,F分别是边AD,DC上的点,且AF⊥BE.
(1)求证:AF=BE;
(2)如图22-②,在正方形ABCD中,M,N,P,Q分别是边AB,BC,CD,DA上的点,且MP⊥NQ,那么MP与NQ是否相等?并说明理由.
附加题(15分,不计入总分)
如图,在△ABC中,点O是边AC上一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)探究线段OE与OF的数量关系并加以证明;
(2)当点O在边AC上运动时,四边形BCFE会是菱形吗?若是,请证明,若不是,请说明理由;
(3)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?
参考答案
一、1.
C
2.A
3.
C
4.
A
5.
B
6.
A
7.
C
8.
A
9.
B
10.
A
二、11.
16
12.
3
13.
4
14.
菱形
15.
20
16.(4,4)
17.
30°
18.
①②③
三、19.(1)解:AD=CF.
(2)证明:因为四边形ABCD是矩形,所以AB∥DC.所以∠AED=∠FDC,AB=CD.又DE=AB,所以DE=CD.因为CF⊥DE,所以∠CFD=∠A=90°.所以△ADE≌△FCD.所以AD=CF.
20.
解:(1)CD
平行
(2)证明:如图,连接BD.
在△ABD和△CDB中,AB=CD,AD=CB,BD=DB,所以△ABD≌△CDB.
所以∠1=∠2,∠3=∠4.
所以AB∥CD,AD∥CB.
所以四边形ABCD是平行四边形.
(3)平行四边形的对边相等
21.(1)证明:因为四边形ABCD是平行四边形,所以AD∥BC.
所以∠EAO=∠FCO.
因为O是AC的中点,所以AO=CO.
又∠EOA=∠FOC,所以△AOE≌△COF.
(2)解:当EF⊥AC时,四边形AFCE是菱形.
理由:由(1)知△AOE≌△COF,所以OE=OF.
又AO=CO,所以四边形AFCE是平行四边形.
所以当EF⊥AC时,平行四边形AFCE是菱形.
22.(1)证明:因为DE∥CA,AE∥BD,所以四边形AODE是平行四边形.
因为四边形ABCD是矩形,所以OA=OC,OD=OB,AC=BD.
所以OA=OD.
所以四边形AODE是菱形.
(2)解:四边形AODE是矩形.
理由:因为DE∥CA,AE∥BD,所以四边形AODE是平行四边形.
因为四边形ABCD是菱形,所以AC⊥BD,即∠AOD=90°.
所以四边形AODE是矩形.
23.
解:小颖的折法:S菱形EFGH=×12×5=30(cm2);
小明的折法:设BE=x
cm,则AE=CE=(12-x)cm.
在Rt△ABE中,由勾股定理,得(12-x)2=52+x2,解得x=,则EC=.
所以S菱形AECF=×5=(cm2).
因为30<,所以小明折出的菱形面积较大.
24.(1)证明:在正方形ABCD中,AB=AD,∠BAE=∠D=90°.所以∠DAF+∠BAF=90°.因为AF⊥BE,所以∠ABE+∠BAF=90°.所以∠ABE=∠DAF.所以△ABE≌△DAF.所以AF=BE.
(2)解:MP=NQ.
理由:过点A作AF∥MP交CD于点F,过点B作BE∥NQ交AD于点E,则与(1)的情况完全相同,可得AF=BE,从而MP=NQ.
附加题
解:(1)OE=OF.
证明:因为CE是∠ACB的平分线,所以∠1=∠2.因为MN∥BC,所以∠1=∠3.所以∠2=∠3.所以OE=OC.同理可证OC=OF.所以OE=OF.
(2)四边形BCFE不可能是菱形.
理由:若四边形BCFE为菱形,则BF⊥EC,而由已知易得FC⊥EC,在平面内过同一点F不可能有两条直线同时垂直于一条直线,所以四边形BCFE不可能是菱形.
(3)当点O运动到AC中点时,OE=OF,OA=OC,则四边形AECF为平行四边形,易证∠ECF=90°,所以四边形AECF为矩形.要使AECF为正方形,必须EF⊥AC.因为EF∥BC,所以只要AC⊥BC即可,所以△ABC应是以∠ACB为直角的直角三角形.所以当点O为AC中点且△ABC是以∠ACB为直角的直角三角形时,四边形AECF是正方形.
图1
图2
图3
图6
图5
图4
图7
图9
图10
图11
y
O
x
C
D
A
B
图14
图15
图12
图13
图19
特殊平行四边形
测试题
一、选择题(每小题3分,共30分)
1.
矩形、菱形、正方形都具有的性质是(
)
A.每一条对角线平分一组对角
B.对角线相等
C.对角线互相平分
D.对角线互相垂直
2.小刚和小东在做一道习题,若四边形ABCD是平行四边形,请补充条件,使得四边形ABCD是矩形.小刚补充的条件是:∠A=∠B;小东补充的条件是:∠A+∠C=180°.你认为下列说法正确的是(
)
A.小刚和小东都正确
B.仅小刚正确
C.仅小东正确
D.小刚和小东都错误
3.
(2015年玉林、防城港)如图1,在□ABCD中,BM平分∠ABC,交CD于点M,且MC=2,□ABCD的周长是14,则DM的长为(
)
A.1
B.2
C.3
D.4
4.
(2015年徐州)如图2,在菱形ABCD中,对角线AC,BD交于点O,E为边AD的中点,菱形ABCD的周长为28,则OE的长为(
)
A.3.5
B.4
C.7
D.14
5.
(2015年日照)小明在学习了正方形之后,给同桌小文出了道题.从下列四个条件:①AB=BC;②∠ABC=90°;③AC=BD;④AC⊥BD中选两个作为补充条件,使□ABCD成为正方形(如图3).现有下列四种选法,你认为其中错误的是(
)
A.①②
B.②③
C.①③
D.②④
6.
(2015年安顺)如图4,点O是矩形ABCD对角线的交点,E是AB上的点,折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为(
)
A.2
B.
C.
D.6
7.
如图5,在菱形ABCD中,M,N分别在AB,CD上,且AM=CN,MN与AC交于点O,连接BO.若∠DAC=28°,则∠OBC的度数为(
)
A.28°
B.52°
C.62°
D.72°
8.
如图6,在△ABC中,BD,CE是△ABC的中线,BD与CE相交于点O,点F,G分别是BO,CO的中点,连接AO.若AO=6
cm,BC=8
cm,则四边形DEFG的周长是(
)
A.14
cm
B.18
cm
C.24
cm
D.28
cm
9.
如图7,两条笔直的公路l1,l2相交于点O,村庄C的村民在公路的旁边建三个加工厂
A,B,D,已知AB=BC=CD=DA=5
km,村庄C到公路l1的距离为4
km,则村庄C到公路l2的距离是(
)
A.
3
km
B.
4
km
C.
5
km
D.
6
km
10.
(2015年丹东)如图8,过矩形ABCD的对角线AC的中点O作EF⊥AC,交BC边于点E,交AD边于点F,分别连接AE,CF.若AB=,∠DCF=30°,则EF的长为( )
A.
2
B.
3
C.
D.
二、填空题(每小题4分,共32分)
11.
如图9,四边形ABCD是菱形,对角线AC和BD相交于点O,AC=4
cm,BD=8
cm,则这个菱形的面积是
cm2.
12.
如图10,□ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点.若AC+BD=24
cm,△OAB的周长是18
cm,则EF=
cm.
13.
如图11,矩形ABCD的对角线相交于O,AB=2,∠AOB=60°,则对角线AC的长为
.
14.
如图12,小聪在作线段AB的垂直平分线时,他是这样操作的:分别以A和B为圆心,大于AB的长为半径画弧,两弧相交于C,D,则直线CD即为所求.根据他的作图方法可知四边形ADBC一定是______.
15.
如图13,平行四边形ABCD的对角线AC,BD相交于点O,BC=9,AC=8,BD=14,则△AOD的周长为________.
16.
(2015年吉林)如图14,在菱形ABCD中,点A在x轴上,点B的坐标为(8,2),点D的坐标为(0,2),则点C的坐标为_______.
17.
(2015年贵港)如图15,在正方形ABCD的外侧,作等边三角形CDE,连接AE,BE,则∠AEB的度数为
.
18.
如图16,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连接AD1,BC1.若∠ACB=30°,AB=1,CC1=x,则下列结论:①△A1AD1≌△CC1B;②当x=1时,四边形ABC1D1是菱形;③当x=2时,△BDD1为等边三角形.其中正确的是
.(填序号)
三、解答题(共58分)
19.
(8分)如图17,四边形ABCD是矩形,E是AB上一点,且DE=AB,过点C作CF⊥DE于点F.
(1)猜想AD与CF的大小关系;
(2)请证明上面的结论.
20.
(9分)(2015年河北)嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图18所示的四边形ABCD,并写出了如下不完整的已知和求证.
(1)在方框中填空,补全已知和求证;
(2)按嘉淇的想法写出证明;
(3)用文字叙述所证命题的逆命题为______________________.
21.
(9分)(2015年郴州)如图19,AC是□ABCD的一条对角线,过AC中点O的直线分别交AD,BC于点E,F.
⑴求证:△AOE≌△COF;
⑵当EF与AC满足什么条件时,四边形AFCE是菱形?并说明理由.
22.
(10分)如图20,矩形ABCD的对角线相交于点O,DE∥CA,AE∥BD.
(1)求证:四边形AODE是菱形;
(2)若将题设中“矩形ABCD”这一条件改为“菱形ABCD”,其余条件不变,则四边形AODE是矩形吗?为什么?
23.(10分)在一张长12
cm、宽5
cm的长方形纸片内,要折出一个菱形.小颖同学按照取两组对边中点的方法折出菱形EFGH(如图21-①),小明同学沿长方形的对角线AC折出∠CAE=∠CAD,∠ACF=∠ACB的方法得到菱形AECF(如图21-②).请问小颖和小明同学的折法中,哪个菱形面积较大?
24.
(12分)如图22-①,在正方形ABCD中,E,F分别是边AD,DC上的点,且AF⊥BE.
(1)求证:AF=BE;
(2)如图22-②,在正方形ABCD中,M,N,P,Q分别是边AB,BC,CD,DA上的点,且MP⊥NQ,那么MP与NQ是否相等?并说明理由.
附加题(15分,不计入总分)
如图,在△ABC中,点O是边AC上一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)探究线段OE与OF的数量关系并加以证明;
(2)当点O在边AC上运动时,四边形BCFE会是菱形吗?若是,请证明,若不是,请说明理由;
(3)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?
参考答案
一、1.
C
2.A
3.
C
4.
A
5.
B
6.
A
7.
C
8.
A
9.
B
10.
A
二、11.
16
12.
3
13.
4
14.
菱形
15.
20
16.(4,4)
17.
30°
18.
①②③
三、19.(1)解:AD=CF.
(2)证明:因为四边形ABCD是矩形,所以AB∥DC.所以∠AED=∠FDC,AB=CD.又DE=AB,所以DE=CD.因为CF⊥DE,所以∠CFD=∠A=90°.所以△ADE≌△FCD.所以AD=CF.
20.
解:(1)CD
平行
(2)证明:如图,连接BD.
在△ABD和△CDB中,AB=CD,AD=CB,BD=DB,所以△ABD≌△CDB.
所以∠1=∠2,∠3=∠4.
所以AB∥CD,AD∥CB.
所以四边形ABCD是平行四边形.
(3)平行四边形的对边相等
21.(1)证明:因为四边形ABCD是平行四边形,所以AD∥BC.
所以∠EAO=∠FCO.
因为O是AC的中点,所以AO=CO.
又∠EOA=∠FOC,所以△AOE≌△COF.
(2)解:当EF⊥AC时,四边形AFCE是菱形.
理由:由(1)知△AOE≌△COF,所以OE=OF.
又AO=CO,所以四边形AFCE是平行四边形.
所以当EF⊥AC时,平行四边形AFCE是菱形.
22.(1)证明:因为DE∥CA,AE∥BD,所以四边形AODE是平行四边形.
因为四边形ABCD是矩形,所以OA=OC,OD=OB,AC=BD.
所以OA=OD.
所以四边形AODE是菱形.
(2)解:四边形AODE是矩形.
理由:因为DE∥CA,AE∥BD,所以四边形AODE是平行四边形.
因为四边形ABCD是菱形,所以AC⊥BD,即∠AOD=90°.
所以四边形AODE是矩形.
23.
解:小颖的折法:S菱形EFGH=×12×5=30(cm2);
小明的折法:设BE=x
cm,则AE=CE=(12-x)cm.
在Rt△ABE中,由勾股定理,得(12-x)2=52+x2,解得x=,则EC=.
所以S菱形AECF=×5=(cm2).
因为30<,所以小明折出的菱形面积较大.
24.(1)证明:在正方形ABCD中,AB=AD,∠BAE=∠D=90°.所以∠DAF+∠BAF=90°.因为AF⊥BE,所以∠ABE+∠BAF=90°.所以∠ABE=∠DAF.所以△ABE≌△DAF.所以AF=BE.
(2)解:MP=NQ.
理由:过点A作AF∥MP交CD于点F,过点B作BE∥NQ交AD于点E,则与(1)的情况完全相同,可得AF=BE,从而MP=NQ.
附加题
解:(1)OE=OF.
证明:因为CE是∠ACB的平分线,所以∠1=∠2.因为MN∥BC,所以∠1=∠3.所以∠2=∠3.所以OE=OC.同理可证OC=OF.所以OE=OF.
(2)四边形BCFE不可能是菱形.
理由:若四边形BCFE为菱形,则BF⊥EC,而由已知易得FC⊥EC,在平面内过同一点F不可能有两条直线同时垂直于一条直线,所以四边形BCFE不可能是菱形.
(3)当点O运动到AC中点时,OE=OF,OA=OC,则四边形AECF为平行四边形,易证∠ECF=90°,所以四边形AECF为矩形.要使AECF为正方形,必须EF⊥AC.因为EF∥BC,所以只要AC⊥BC即可,所以△ABC应是以∠ACB为直角的直角三角形.所以当点O为AC中点且△ABC是以∠ACB为直角的直角三角形时,四边形AECF是正方形.
图1
图2
图3
图6
图5
图4
图7
图9
图10
图11
y
O
x
C
D
A
B
图14
图15
图12
图13
图19
