第08周 4.3探索三角形全等的条件---4.5利用三角形全等距离同步测试
文档属性
| 名称 | 第08周 4.3探索三角形全等的条件---4.5利用三角形全等距离同步测试 |

|
|
| 格式 | zip | ||
| 文件大小 | 91.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-14 00:00:00 | ||
图片预览

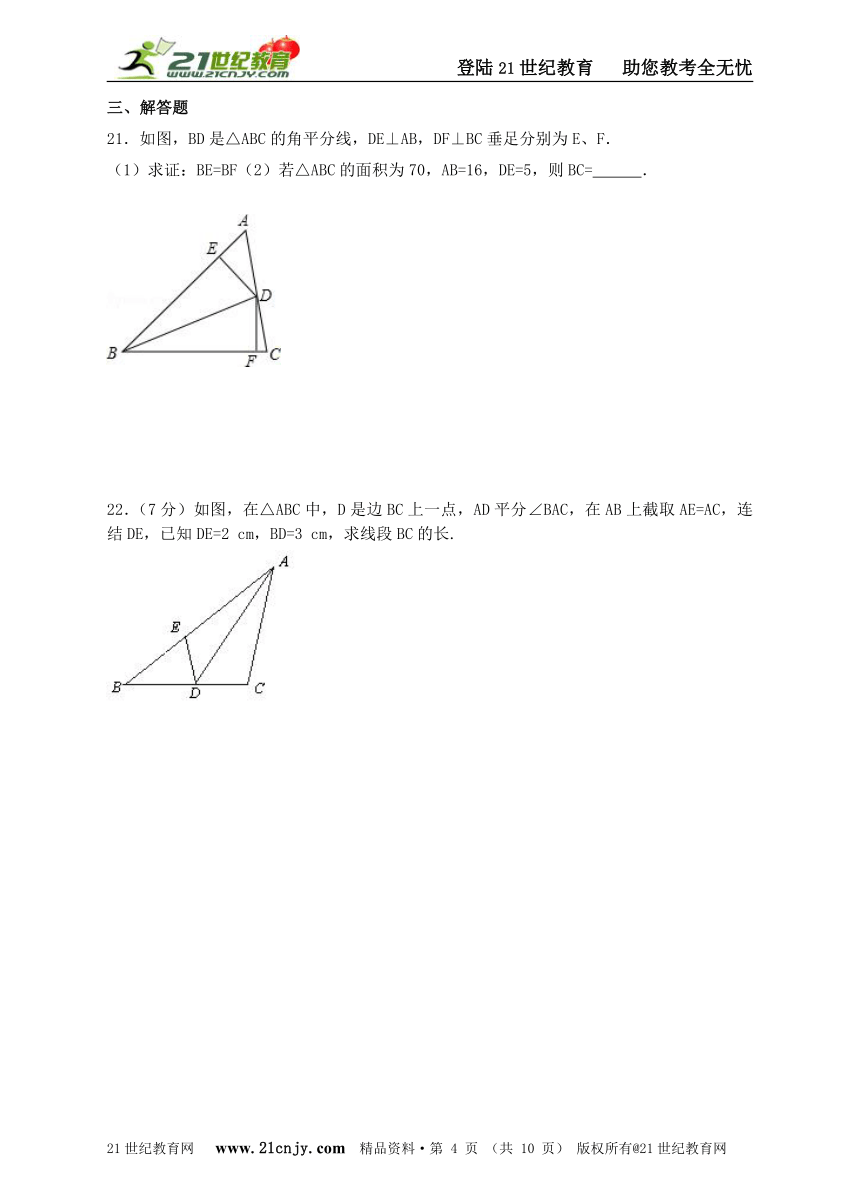
文档简介
【北师大版七年级数学(下)周周测】
第8周测试卷
(测试范围:4.3探索三角形全等的条件---4.5利用三角形全等距离)
班级:___________ 姓名:___________ 得分:___________
一、选择题:(每小题3分共30分)
1.在△ABC和△DEF中,已知AC=DF,BC=EF,要使△ABC≌△DEF,还需要的条件是( )
A、∠A=∠D B、∠C=∠F C、∠B=∠E D、∠C=∠D
2.不能判断两个三个角形全等的条件是…
A. 两角及一边对应相等 B. 两边及夹角对应相等
C. 三条边对应相等 D. 三个角对应相等
3.如图,在△ABC和△DEF中,已知AC=DF,BC=EF,要使△ABC≌△DEF,还需要的条件是( )21·cn·jy·com
A.∠A=∠D B.∠ACB=∠F C.∠B=∠DEF D.∠ACB=∠D
4.尺规作图是指( )
A、用直尺规范作图
B、用刻度尺和圆规作图
C、用没有刻度的直尺和圆规作图
D、直尺和圆规是作图工具
5.如图,AD⊥BC,ED⊥AB,表示点A到直线DE距离的是( )
A.线段AD的长度 B.线段AE的长度
C.线段BE的长度 D.线段DE的长度
6.下列判定直角三角形全等的方法,不正确的是 ( )
A.两条直角边对应相等 B.斜边和一锐角对应相等
C.斜边和一条直角边对应相等 D.两锐角相等
7.下列条件中,能判定两个直角三角形全等的是( )
A.一锐角对应相等 B.两锐角对应相等
C.一条边对应相等 D.两条直角边对应相等
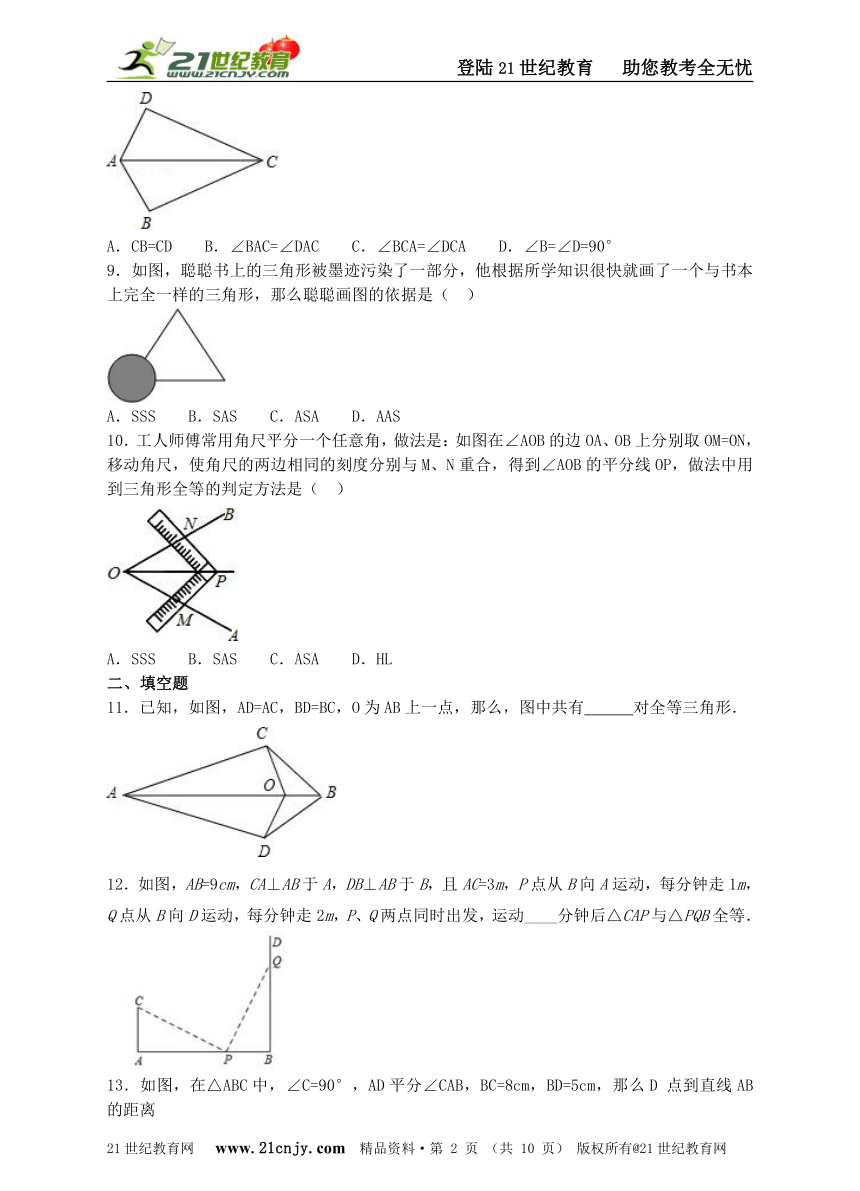
8.如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
A.CB=CD B.∠BAC=∠DAC C.∠BCA=∠DCA D.∠B=∠D=90°
9.如图,聪聪书上的三角形被墨迹污染了一部分,他根据所学知识很快就画了一个与书本上完全一样的三角形,那么聪聪画图的依据是( )21教育网
A.SSS B.SAS C.ASA D.AAS
10.工人师傅常用角尺平分一个任意角,做法是:如图在∠AOB的边OA、OB上分别取OM=ON,移动角尺,使角尺的两边相同的刻度分别与M、N重合,得到∠AOB的平分线OP,做法中用到三角形全等的判定方法是( )21cnjy.com
A.SSS B.SAS C.ASA D.HL
二、填空题
11.已知,如图,AD=AC,BD=BC,O为AB上一点,那么,图中共有 对全等三角形.
12.如图,AB=9cm,CA⊥AB于A,DB⊥AB于B,且AC=3m,P点从B向A运动,每分钟走1m,Q点从B向D运动,每分钟走2m,P、Q两点同时出发,运动____分钟后△CAP与△PQB全等.
13.如图,在△ABC中,∠C=90°,AD平分∠CAB,BC=8cm,BD=5cm,那么D点到直线AB的距离www.21-cn-jy.com
是 cm。
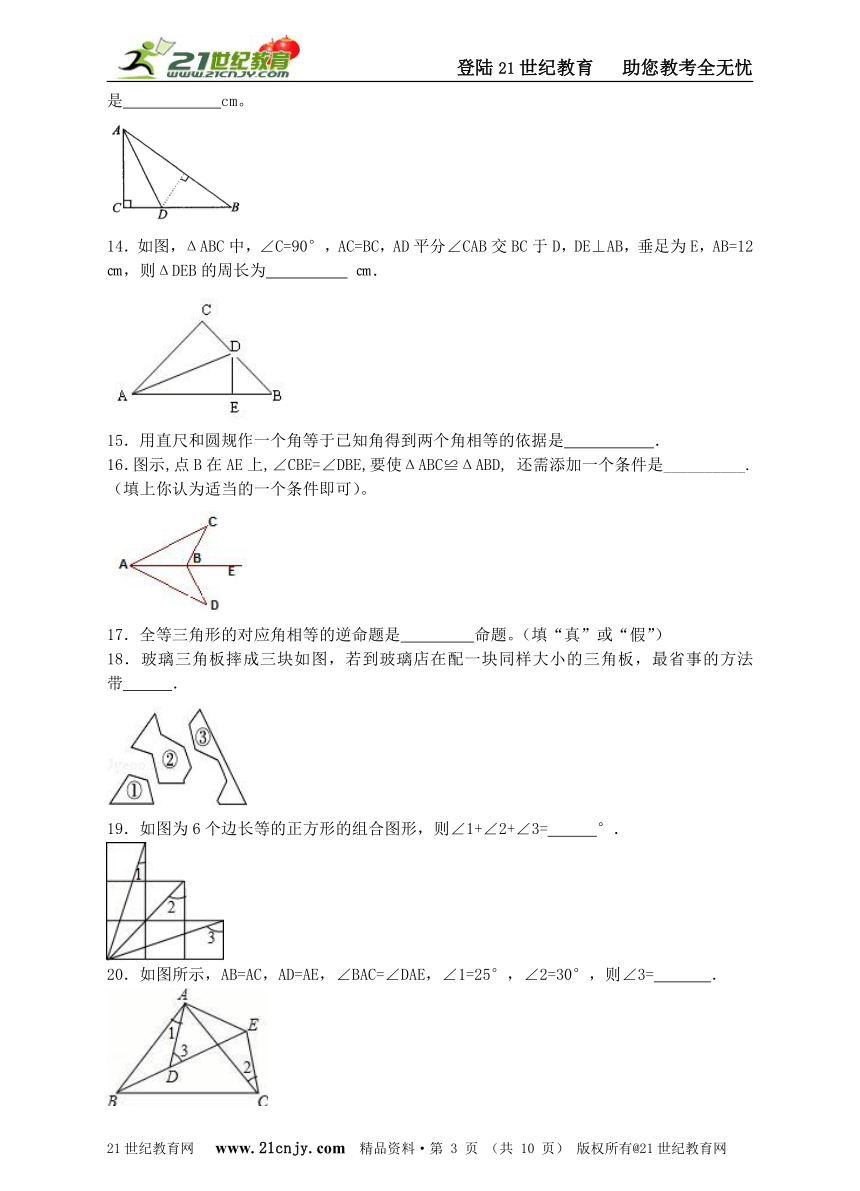
14.如图,ΔABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB,垂足为E,AB=12㎝,则ΔDEB的周长为 ㎝.【来源:21·世纪·教育·网】
15.用直尺和圆规作一个角等于已知角得到两个角相等的依据是 .
16.图示,点B在AE上,∠CBE=∠DBE,要使ΔABC≌ΔABD, 还需添加一个条件是__________.(填上你认为适当的一个条件即可)。2-1-c-n-j-y
17.全等三角形的对应角相等的逆命题是 命题。(填“真”或“假”)
18.玻璃三角板摔成三块如图,若到玻璃店在配一块同样大小的三角板,最省事的方法带 .
19.如图为6个边长等的正方形的组合图形,则∠1+∠2+∠3= °.
20.如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3= .
三、解答题
21.如图,BD是△ABC的角平分线,DE⊥AB,DF⊥BC垂足分别为E、F.
(1)求证:BE=BF(2)若△ABC的面积为70,AB=16,DE=5,则BC= .
22.(7分)如图,在△ABC中,D是边BC上一点,AD平分∠BAC,在AB上截取AE=AC,连结DE,已知DE=2 cm,BD=3 cm,求线段BC的长.【出处:21教育名师】
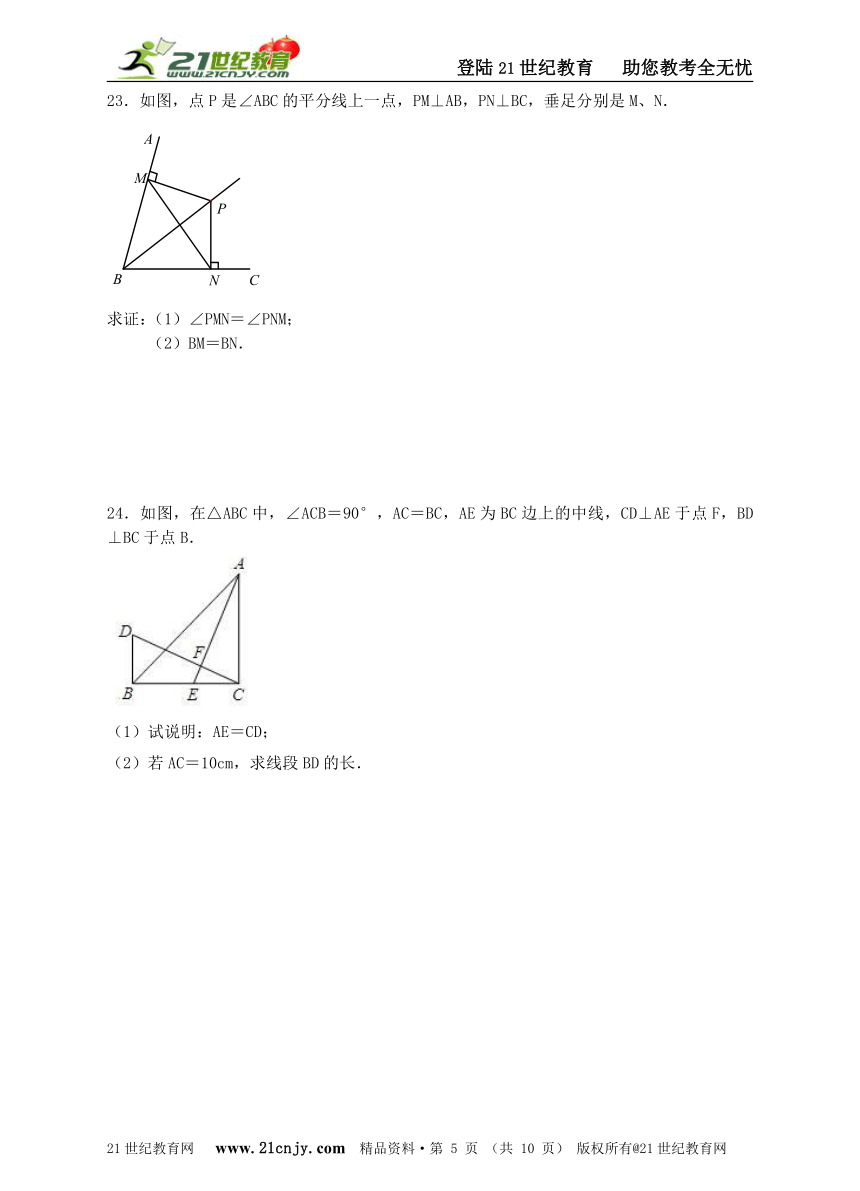
23.如图,点P是∠ABC的平分线上一点,PM⊥AB,PN⊥BC,垂足分别是M、N.
求证:(1)∠PMN=∠PNM;
(2)BM=BN.
24.如图,在△ABC中,∠ACB=90°,AC=BC,AE为BC边上的中线,CD⊥AE于点F,BD⊥BC于点B.【来源:21cnj*y.co*m】
(1)试说明:AE=CD;
(2)若AC=10cm,求线段BD的长.
参考答案
1.B
【解析】
试题分析:根据两边及夹角对应相等的两个三角形全等可得需要添加的条件为∠C=∠F.
2.D
【解析】
试题分析:全等三角形的判定方法有SSS、SAS、ASA、AAS四种.
3.B
【解析】
试题分析:本题要判定△ABC≌△DEF,有AC=DF,BC=EF,可以加∠ACB=∠F,就可以用SAS判定△ABC≌△DEF.21·世纪*教育网
解:A,添加∠A=∠D,满足SSA,不能判定△ABC≌△DEF;
B,添加∠ACB=∠F,满足SAS,能判定△ABC≌△DEF;
C,添加∠B=∠DEF,满足SSA,不能判定△ABC≌△DEF;
D,添加∠ACB=∠D,两角不是对应角,不能判定△ABC≌△DEF;
故选B.
4.C
【解析】本题考查了尺规作图的主要工具,熟练记住尺规作图实用工具中直尺是无刻度直尺是解题关键.尺规作图所用的作图工具是指不带刻度的直尺和圆规,故选:C【版权所有:21教育】
5.B.
【解析】
试题分析:∵ED⊥AB,∴点A到直线DE距离的是线段AE的长度.故选B.
6.D.
【解析】
试题解析:如果在两个直角三角形中,两条直角边对应相等, 那么根据SAS即可判断两三角形全等,故选项A正确. 21教育名师原创作品
如果如果在两个直角三角形中,斜边和一锐角对应相等, 那么根据AAS也可判断两三角形全等,故选项B正确. 21*cnjy*com
如果如果在两个直角三角形中,斜边和一直角边对应相等, 那么根据HL也可判断两三角形全等,故选项C正确.
故选D.
7.D
【解析】
试题分析:三角形全等可以利用SAS、SSS、ASA和AAS来进行判定,直角三角形还可以用HL定理来进行判定.本题中D选项可以利用SAS来进行判定三角形全等.
8.C
【解析】
试题分析:本题要判定△ABC≌△ADC,已知AB=AD,AC是公共边,具备了两组边对应相等,故添加CB=CD、∠BAC=∠DAC、∠B=∠D=90°后可分别根据SSS、SAS、HL能判定△ABC≌△ADC,而添加∠BCA=∠DCA后则不能.2·1·c·n·j·y
解:A、添加CB=CD,根据SSS,能判定△ABC≌△ADC,故A选项不符合题意;
B、添加∠BAC=∠DAC,根据SAS,能判定△ABC≌△ADC,故B选项不符合题意;
C、添加∠BCA=∠DCA时,不能判定△ABC≌△ADC,故C选项符合题意;
D、添加∠B=∠D=90°,根据HL,能判定△ABC≌△ADC,故D选项不符合题意;
故选:C.
9.C
【解析】
试题分析:根据图象,三角形有两角和它们的夹边是完整的,所以可以根据“角边角”画出.
解:根据题意,三角形的两角和它们的夹边是完整的,所以可以利用“角边角”定理作出完全一样的三角形.
故选:C.
10.A
【解析】
试题分析:已知两三角形三边分别相等,可考虑SSS证明三角形全等,从而证明角相等.
解﹕做法中用到的三角形全等的判定方法是SSS
证明如下
∵OM=ON
PM=PN
OP=OP
∴△ONP≌△OMP(SSS)
所以∠NOP=∠MOP
故OP为∠AOB的平分线.
故选:A.
11.3
【解析】
试题分析:根据三角形全等的判定定理可得:△ACO≌△AOD,△BCO≌△BOD和△ACB≌△ADB.
12.3
【解析】
∵CA⊥AB于A,DB⊥AB于B,∴∠A=∠B=90°,设运动x分钟后△CAP与△PQB全等;
则BP=xm,BQ=2xm,则AP=(9﹣x)m,分两种情况:
BP=AC,则x=3,AP=9﹣3=6,BQ=6,AP=BQ,∴△CAP≌△PBQ;
BP=AP,则9﹣x=x,解得:x=4.5,BQ=9≠AC,此时△CAP与△PQB不全等;
综上所述:运动3分钟后△CAP与△PQB全等;
故答案为:3.
13.3
【解析】
试题分析:根据BC=8cm,BD=5cm可得:CD=8-5=3cm,根据角平分线上的点到角两边的距离相等可得点D到直线AB的距离等于CD的长度.www-2-1-cnjy-com
14.12.
【解析】
试题分析:由题目的已知条件应用AAS易证△CAD≌△EAD.得到DE=CD,于是BD+DE=BC=AC=AE,则周长可利用对应边相等代换求解.
试题解析:∵AD平分∠CAB,∠C=90°,DE⊥AB,
∴∠CAD=∠BAD,∠C=∠AED.
又∵AD=AD,
在△CAD和△EAD中
∴△CAD≌△EAD,
∴AC=AE,CD=DE.
∵AC=BC,
∴BC=AE.
∴△DEB的周长为DB+DE+EB=DB+CD+EB=CB+BE=AE+BE=12cm.
15.SSS.
【解析】
试题分析:本题考查的是基本作图及全等三角形的判定与性质;由全等得到角相等是用的全等三角形的性质,熟练掌握三角形全等的性质是正确解答本题的关键.我们可以通过其作图的步骤来进行分析,作图时满足了三条边对应相等,于是我们可以判定是运用SSS.
解:作图的步骤:
①以O为圆心,任意长为半径画弧,分别交OA、OB于点C、D;
②任意作一点O′,作射线O′A′,以O′为圆心,OC长为半径画弧,交O′A′于点C′;
③以C′为圆心,CD长为半径画弧,交前弧于点D′;
④过点D′作射线O′B′.
所以∠A′O′B′就是与∠AOB相等的角;
在△OCD与△O′C′D′,
,
∴△OCD≌△O′C′D′(SSS),
∴∠A′O′B′=∠AOB,
故答案为SSS.
16.BC=BD(答案不唯一)
【解析】
试题分析:根据∠CBE=∠DBE可得∠ABC=∠ABD,如果利用SAS来判定可以添加BC=BD,如果利用ASA来判定可以添加∠CAB=∠DAB,如果利用AAS来判定可以添加∠C=∠D.
17.假
【解析】
试题分析:原命题的逆命题为:对应角相等的两个三角形全等,根据三角形全等的判定条件可知这是一个假命题.21*cnjy*com
考点:真假命题的判定
18.③.
【解析】
试题分析:根据全等三角形的判定方法ASA即可得出结果.
解:带③去符合“角边角”可以配一块同样大小的三角板.
故答案为:③.
19.135.
【解析】
试题分析:观察图形可知∠1与∠3互余,∠2是直角的一半,利用这些关系可解此题.
解:观察图形可知:△ABC≌△BDE,
∴∠1=∠DBE,
又∵∠DBE+∠3=90°,
∴∠1+∠3=90°.
∵∠2=45°,
∴∠1+∠2+∠3=∠1+∠3+∠2=90°+45°=135°.
故填135.
20.55°.
【解析】
试题分析:证得∠BAD=∠EAC,根据边角边证得△BAD≌△EAC,根据全等三角形的性质可得∠2=∠ABD=30°,根据三角形的外角性质求出∠3=∠1+∠ABD=25°+30°=55°.
故答案为:55°.
21.(1)见解析;(2)12
【解析】
试题分析:(1)由角平分线的对称性直接证明△DBE≌△DBF即可;
(2)先算出三角形ABD的面积,再得出三角形BCD的面积,高DF=DE=5,从而直接算出BC.
(1)证明:∵DE⊥AB,DF⊥BC,
∴∠BED=∠BFD=90°,
∵BD是△ABC的角平分线,
∴∠EBD=∠FBD,
又∵BD=BD,
∴△DBE≌△DBF,
∴BE=BF;
(2)解:∵BD是△ABC的角平分线,DE⊥AB,DF⊥BC,
∴DF=DE=5,
∴,
∴=70﹣40=30,
∴BC=12.
故答案为12.
22.5 cm
【解析】
试题分析:由题意证得△ACD≌△AED∴ 得到CD=DE,∴BC=DB+CD带入数据即可.
试题解析:∵AD平分∠BAC ∴∠BAD=∠CAD , 又∵AE=AC,
AD=AD ∴△ACD≌△AED(SAS) ∴CD=DE=2∴BC=DB+CD=3+2=5(cm)
23.(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)根据角平分线上的点到角两边的距离相等得出PM=PN,从而得出∠PMN=∠PNM;(2)根据∠PMB=∠PNB以及∠PMN=∠PNM得出∠BMN=∠BNM,从而得出答案.
试题解析:(1)∵PB是角平分线,PM⊥AB,PN⊥BC ∴PM=PN ∴∠PMN=∠PNM
(2)∵90°-∠PMN=90°-∠PNM 即∠BMN=∠BNM ∴BM=BN
24.(1)证明见试题解析;(2)5㎝.
【解析】
试题分析:(1)证明△DBC≌△ECA即可;
(2)由(1)得BD=EC=BC=AC,且AC=10cm,即可求出BD的长.
试题解析:(1)证明:∵DB⊥BC,CF⊥AE,∴∠DCB+∠D=∠DCB+∠AEC=90°,∴∠D=∠AEC.又∵∠DBC=∠ECA=90°,且BC=CA,∴△DBC≌△ECA(AAS),∴AE=CD;
(2)解:由(1)得AE=CD,AC=BC,∴Rt△CDB≌Rt△AEC(HL),∴BD=EC=BC=AC,且AC=10cm,∴BD=5cm.21世纪教育网版权所有
第8周测试卷
(测试范围:4.3探索三角形全等的条件---4.5利用三角形全等距离)
班级:___________ 姓名:___________ 得分:___________
一、选择题:(每小题3分共30分)
1.在△ABC和△DEF中,已知AC=DF,BC=EF,要使△ABC≌△DEF,还需要的条件是( )
A、∠A=∠D B、∠C=∠F C、∠B=∠E D、∠C=∠D
2.不能判断两个三个角形全等的条件是…
A. 两角及一边对应相等 B. 两边及夹角对应相等
C. 三条边对应相等 D. 三个角对应相等
3.如图,在△ABC和△DEF中,已知AC=DF,BC=EF,要使△ABC≌△DEF,还需要的条件是( )21·cn·jy·com
A.∠A=∠D B.∠ACB=∠F C.∠B=∠DEF D.∠ACB=∠D
4.尺规作图是指( )
A、用直尺规范作图
B、用刻度尺和圆规作图
C、用没有刻度的直尺和圆规作图
D、直尺和圆规是作图工具
5.如图,AD⊥BC,ED⊥AB,表示点A到直线DE距离的是( )
A.线段AD的长度 B.线段AE的长度
C.线段BE的长度 D.线段DE的长度
6.下列判定直角三角形全等的方法,不正确的是 ( )
A.两条直角边对应相等 B.斜边和一锐角对应相等
C.斜边和一条直角边对应相等 D.两锐角相等
7.下列条件中,能判定两个直角三角形全等的是( )
A.一锐角对应相等 B.两锐角对应相等
C.一条边对应相等 D.两条直角边对应相等
8.如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
A.CB=CD B.∠BAC=∠DAC C.∠BCA=∠DCA D.∠B=∠D=90°
9.如图,聪聪书上的三角形被墨迹污染了一部分,他根据所学知识很快就画了一个与书本上完全一样的三角形,那么聪聪画图的依据是( )21教育网
A.SSS B.SAS C.ASA D.AAS
10.工人师傅常用角尺平分一个任意角,做法是:如图在∠AOB的边OA、OB上分别取OM=ON,移动角尺,使角尺的两边相同的刻度分别与M、N重合,得到∠AOB的平分线OP,做法中用到三角形全等的判定方法是( )21cnjy.com
A.SSS B.SAS C.ASA D.HL
二、填空题
11.已知,如图,AD=AC,BD=BC,O为AB上一点,那么,图中共有 对全等三角形.
12.如图,AB=9cm,CA⊥AB于A,DB⊥AB于B,且AC=3m,P点从B向A运动,每分钟走1m,Q点从B向D运动,每分钟走2m,P、Q两点同时出发,运动____分钟后△CAP与△PQB全等.
13.如图,在△ABC中,∠C=90°,AD平分∠CAB,BC=8cm,BD=5cm,那么D点到直线AB的距离www.21-cn-jy.com
是 cm。
14.如图,ΔABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB,垂足为E,AB=12㎝,则ΔDEB的周长为 ㎝.【来源:21·世纪·教育·网】
15.用直尺和圆规作一个角等于已知角得到两个角相等的依据是 .
16.图示,点B在AE上,∠CBE=∠DBE,要使ΔABC≌ΔABD, 还需添加一个条件是__________.(填上你认为适当的一个条件即可)。2-1-c-n-j-y
17.全等三角形的对应角相等的逆命题是 命题。(填“真”或“假”)
18.玻璃三角板摔成三块如图,若到玻璃店在配一块同样大小的三角板,最省事的方法带 .
19.如图为6个边长等的正方形的组合图形,则∠1+∠2+∠3= °.
20.如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3= .
三、解答题
21.如图,BD是△ABC的角平分线,DE⊥AB,DF⊥BC垂足分别为E、F.
(1)求证:BE=BF(2)若△ABC的面积为70,AB=16,DE=5,则BC= .
22.(7分)如图,在△ABC中,D是边BC上一点,AD平分∠BAC,在AB上截取AE=AC,连结DE,已知DE=2 cm,BD=3 cm,求线段BC的长.【出处:21教育名师】
23.如图,点P是∠ABC的平分线上一点,PM⊥AB,PN⊥BC,垂足分别是M、N.
求证:(1)∠PMN=∠PNM;
(2)BM=BN.
24.如图,在△ABC中,∠ACB=90°,AC=BC,AE为BC边上的中线,CD⊥AE于点F,BD⊥BC于点B.【来源:21cnj*y.co*m】
(1)试说明:AE=CD;
(2)若AC=10cm,求线段BD的长.
参考答案
1.B
【解析】
试题分析:根据两边及夹角对应相等的两个三角形全等可得需要添加的条件为∠C=∠F.
2.D
【解析】
试题分析:全等三角形的判定方法有SSS、SAS、ASA、AAS四种.
3.B
【解析】
试题分析:本题要判定△ABC≌△DEF,有AC=DF,BC=EF,可以加∠ACB=∠F,就可以用SAS判定△ABC≌△DEF.21·世纪*教育网
解:A,添加∠A=∠D,满足SSA,不能判定△ABC≌△DEF;
B,添加∠ACB=∠F,满足SAS,能判定△ABC≌△DEF;
C,添加∠B=∠DEF,满足SSA,不能判定△ABC≌△DEF;
D,添加∠ACB=∠D,两角不是对应角,不能判定△ABC≌△DEF;
故选B.
4.C
【解析】本题考查了尺规作图的主要工具,熟练记住尺规作图实用工具中直尺是无刻度直尺是解题关键.尺规作图所用的作图工具是指不带刻度的直尺和圆规,故选:C【版权所有:21教育】
5.B.
【解析】
试题分析:∵ED⊥AB,∴点A到直线DE距离的是线段AE的长度.故选B.
6.D.
【解析】
试题解析:如果在两个直角三角形中,两条直角边对应相等, 那么根据SAS即可判断两三角形全等,故选项A正确. 21教育名师原创作品
如果如果在两个直角三角形中,斜边和一锐角对应相等, 那么根据AAS也可判断两三角形全等,故选项B正确. 21*cnjy*com
如果如果在两个直角三角形中,斜边和一直角边对应相等, 那么根据HL也可判断两三角形全等,故选项C正确.
故选D.
7.D
【解析】
试题分析:三角形全等可以利用SAS、SSS、ASA和AAS来进行判定,直角三角形还可以用HL定理来进行判定.本题中D选项可以利用SAS来进行判定三角形全等.
8.C
【解析】
试题分析:本题要判定△ABC≌△ADC,已知AB=AD,AC是公共边,具备了两组边对应相等,故添加CB=CD、∠BAC=∠DAC、∠B=∠D=90°后可分别根据SSS、SAS、HL能判定△ABC≌△ADC,而添加∠BCA=∠DCA后则不能.2·1·c·n·j·y
解:A、添加CB=CD,根据SSS,能判定△ABC≌△ADC,故A选项不符合题意;
B、添加∠BAC=∠DAC,根据SAS,能判定△ABC≌△ADC,故B选项不符合题意;
C、添加∠BCA=∠DCA时,不能判定△ABC≌△ADC,故C选项符合题意;
D、添加∠B=∠D=90°,根据HL,能判定△ABC≌△ADC,故D选项不符合题意;
故选:C.
9.C
【解析】
试题分析:根据图象,三角形有两角和它们的夹边是完整的,所以可以根据“角边角”画出.
解:根据题意,三角形的两角和它们的夹边是完整的,所以可以利用“角边角”定理作出完全一样的三角形.
故选:C.
10.A
【解析】
试题分析:已知两三角形三边分别相等,可考虑SSS证明三角形全等,从而证明角相等.
解﹕做法中用到的三角形全等的判定方法是SSS
证明如下
∵OM=ON
PM=PN
OP=OP
∴△ONP≌△OMP(SSS)
所以∠NOP=∠MOP
故OP为∠AOB的平分线.
故选:A.
11.3
【解析】
试题分析:根据三角形全等的判定定理可得:△ACO≌△AOD,△BCO≌△BOD和△ACB≌△ADB.
12.3
【解析】
∵CA⊥AB于A,DB⊥AB于B,∴∠A=∠B=90°,设运动x分钟后△CAP与△PQB全等;
则BP=xm,BQ=2xm,则AP=(9﹣x)m,分两种情况:
BP=AC,则x=3,AP=9﹣3=6,BQ=6,AP=BQ,∴△CAP≌△PBQ;
BP=AP,则9﹣x=x,解得:x=4.5,BQ=9≠AC,此时△CAP与△PQB不全等;
综上所述:运动3分钟后△CAP与△PQB全等;
故答案为:3.
13.3
【解析】
试题分析:根据BC=8cm,BD=5cm可得:CD=8-5=3cm,根据角平分线上的点到角两边的距离相等可得点D到直线AB的距离等于CD的长度.www-2-1-cnjy-com
14.12.
【解析】
试题分析:由题目的已知条件应用AAS易证△CAD≌△EAD.得到DE=CD,于是BD+DE=BC=AC=AE,则周长可利用对应边相等代换求解.
试题解析:∵AD平分∠CAB,∠C=90°,DE⊥AB,
∴∠CAD=∠BAD,∠C=∠AED.
又∵AD=AD,
在△CAD和△EAD中
∴△CAD≌△EAD,
∴AC=AE,CD=DE.
∵AC=BC,
∴BC=AE.
∴△DEB的周长为DB+DE+EB=DB+CD+EB=CB+BE=AE+BE=12cm.
15.SSS.
【解析】
试题分析:本题考查的是基本作图及全等三角形的判定与性质;由全等得到角相等是用的全等三角形的性质,熟练掌握三角形全等的性质是正确解答本题的关键.我们可以通过其作图的步骤来进行分析,作图时满足了三条边对应相等,于是我们可以判定是运用SSS.
解:作图的步骤:
①以O为圆心,任意长为半径画弧,分别交OA、OB于点C、D;
②任意作一点O′,作射线O′A′,以O′为圆心,OC长为半径画弧,交O′A′于点C′;
③以C′为圆心,CD长为半径画弧,交前弧于点D′;
④过点D′作射线O′B′.
所以∠A′O′B′就是与∠AOB相等的角;
在△OCD与△O′C′D′,
,
∴△OCD≌△O′C′D′(SSS),
∴∠A′O′B′=∠AOB,
故答案为SSS.
16.BC=BD(答案不唯一)
【解析】
试题分析:根据∠CBE=∠DBE可得∠ABC=∠ABD,如果利用SAS来判定可以添加BC=BD,如果利用ASA来判定可以添加∠CAB=∠DAB,如果利用AAS来判定可以添加∠C=∠D.
17.假
【解析】
试题分析:原命题的逆命题为:对应角相等的两个三角形全等,根据三角形全等的判定条件可知这是一个假命题.21*cnjy*com
考点:真假命题的判定
18.③.
【解析】
试题分析:根据全等三角形的判定方法ASA即可得出结果.
解:带③去符合“角边角”可以配一块同样大小的三角板.
故答案为:③.
19.135.
【解析】
试题分析:观察图形可知∠1与∠3互余,∠2是直角的一半,利用这些关系可解此题.
解:观察图形可知:△ABC≌△BDE,
∴∠1=∠DBE,
又∵∠DBE+∠3=90°,
∴∠1+∠3=90°.
∵∠2=45°,
∴∠1+∠2+∠3=∠1+∠3+∠2=90°+45°=135°.
故填135.
20.55°.
【解析】
试题分析:证得∠BAD=∠EAC,根据边角边证得△BAD≌△EAC,根据全等三角形的性质可得∠2=∠ABD=30°,根据三角形的外角性质求出∠3=∠1+∠ABD=25°+30°=55°.
故答案为:55°.
21.(1)见解析;(2)12
【解析】
试题分析:(1)由角平分线的对称性直接证明△DBE≌△DBF即可;
(2)先算出三角形ABD的面积,再得出三角形BCD的面积,高DF=DE=5,从而直接算出BC.
(1)证明:∵DE⊥AB,DF⊥BC,
∴∠BED=∠BFD=90°,
∵BD是△ABC的角平分线,
∴∠EBD=∠FBD,
又∵BD=BD,
∴△DBE≌△DBF,
∴BE=BF;
(2)解:∵BD是△ABC的角平分线,DE⊥AB,DF⊥BC,
∴DF=DE=5,
∴,
∴=70﹣40=30,
∴BC=12.
故答案为12.
22.5 cm
【解析】
试题分析:由题意证得△ACD≌△AED∴ 得到CD=DE,∴BC=DB+CD带入数据即可.
试题解析:∵AD平分∠BAC ∴∠BAD=∠CAD , 又∵AE=AC,
AD=AD ∴△ACD≌△AED(SAS) ∴CD=DE=2∴BC=DB+CD=3+2=5(cm)
23.(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)根据角平分线上的点到角两边的距离相等得出PM=PN,从而得出∠PMN=∠PNM;(2)根据∠PMB=∠PNB以及∠PMN=∠PNM得出∠BMN=∠BNM,从而得出答案.
试题解析:(1)∵PB是角平分线,PM⊥AB,PN⊥BC ∴PM=PN ∴∠PMN=∠PNM
(2)∵90°-∠PMN=90°-∠PNM 即∠BMN=∠BNM ∴BM=BN
24.(1)证明见试题解析;(2)5㎝.
【解析】
试题分析:(1)证明△DBC≌△ECA即可;
(2)由(1)得BD=EC=BC=AC,且AC=10cm,即可求出BD的长.
试题解析:(1)证明:∵DB⊥BC,CF⊥AE,∴∠DCB+∠D=∠DCB+∠AEC=90°,∴∠D=∠AEC.又∵∠DBC=∠ECA=90°,且BC=CA,∴△DBC≌△ECA(AAS),∴AE=CD;
(2)解:由(1)得AE=CD,AC=BC,∴Rt△CDB≌Rt△AEC(HL),∴BD=EC=BC=AC,且AC=10cm,∴BD=5cm.21世纪教育网版权所有
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
