7.4 实践与探索 同步练习
图片预览


文档简介
7.4 实践与探索
核心笔记: 列二元一次方程组解应用题的一般步骤:
(1)弄清题意和题目中的数量关系,用字母(如x、y、z)表示题目中的未知数;
(2)找出能够表达应用题全部含义的相等关系;
(3)根据这些相等关系列出需要的代数式,从而列出方程并组成方程组;
(4)解这个方程组,求出未知数的值;
(5)检验所得方程组的解是否正确和符合题目的实际意义,并写出答案(包括单位名称).
基础训练
1.如图,10块相同的长方形墙砖拼成一个大长方形,设长方形墙砖的长和宽分别为x厘米和y厘米,则依题意列方程组正确的是( )
A. B.
C. D.
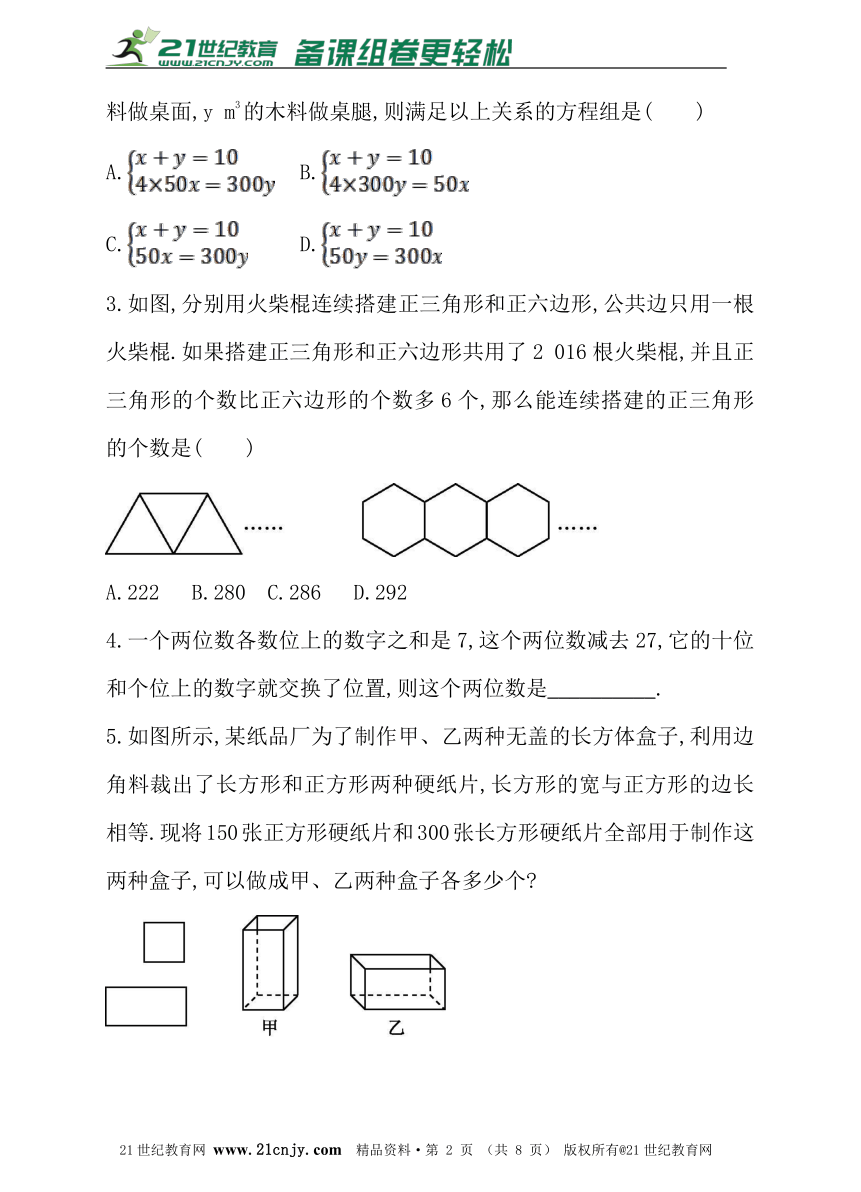
2.一张方桌由一个桌面与四条桌腿组成,1 m3木料可以做桌面50个或桌腿300条,现有10 m3的木料,能恰好做成方桌多少张?设用x m3的木料做桌面,y m3的木料做桌腿,则满足以上关系的方程组是( )
A. B.
C. D.
3.如图,分别用火柴棍连续搭建正三角形和正六边形,公共边只用一根火柴棍.如果搭建正三角形和正六边形共用了2 016根火柴棍,并且正三角形的个数比正六边形的个数多6个,那么能连续搭建的正三角形的个数是( )21·cn·jy·com
A.222 B.280 C.286 D.292
4.一个两位数各数位上的数字之和是7,这个两位数减去27,它的十位和个位上的数字就交换了位置,则这个两位数是__________.
5.如图所示,某纸品厂为了制作甲、乙两种无盖的长方体盒子,利用边角料裁出了长方形和正方形两种硬纸片,长方形的宽与正方形的边长相等.现将150张正方形硬纸片和300张长方形硬纸片全部用于制作这两种盒子,可以做成甲、乙两种盒子各多少个?2·1·c·n·j·y
6.某球迷协会组织36名球迷拟租乘汽车赴比赛场地,为中国男子足球队呐喊助威,可利用的汽车有两种:一种每辆可乘8人,另一种每辆可乘4人,要求租用的汽车不留空座,也不超载. 【来源:21·世纪·教育·网】
(1)请你给出三种不同的租车方案;
(2)若8个座位的汽车租金是300元/天,4个座位的汽车租金是200元/天,请你设计费用最少的租车方案.21·世纪*教育网
培优提升
1.陈老师打算购买气球装扮学校六一儿童节活动会场,气球的种类有笑脸和爱心两种,两种气球的价格不同,但同一种气球的价格相同,由于会场布置需要,购买时以一束(4个气球)为单位,已知第一、二束气球的价格如图所示,则第三束气球的价格为( )www-2-1-cnjy-com
A.19元 B.18元 C.16元 D.15元
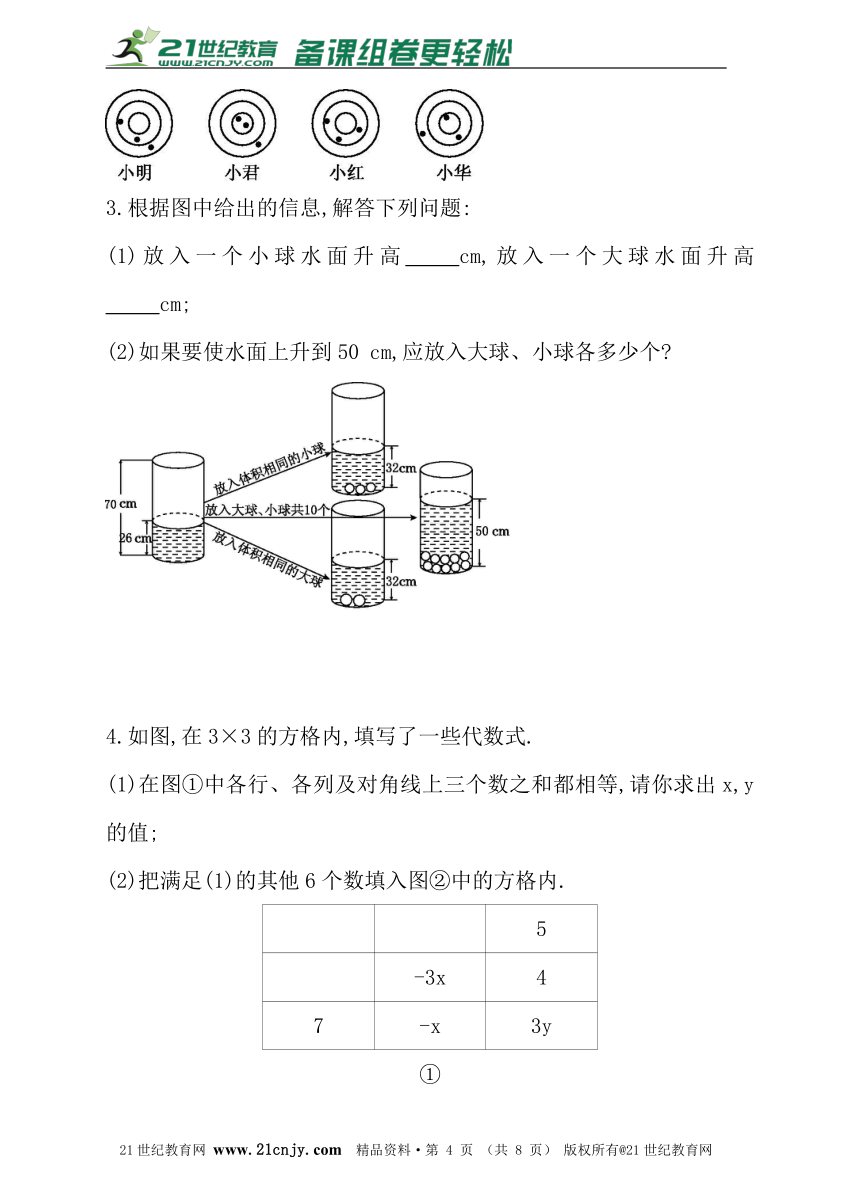
2.某校组织了一次游戏:每位选手朝特制的靶子上各投三次飞镖,在同一圆环内得分相同.如图所示,小明、小君、小红的成绩分别是29分、43分和33分,则小华的成绩是________分.2-1-c-n-j-y
3.根据图中给出的信息,解答下列问题:
(1)放入一个小球水面升高_____cm,放入一个大球水面升高_____cm;?
(2)如果要使水面上升到50 cm,应放入大球、小球各多少个?
4.如图,在3×3的方格内,填写了一些代数式.
(1)在图①中各行、各列及对角线上三个数之和都相等,请你求出x,y的值;
(2)把满足(1)的其他6个数填入图②中的方格内.
5
-3x
4
7
-x
3y
①
5
4
7
②
5.小明新买了一辆自行车,他在网上查找了相应型号自行车轮胎使用有关小知识,如图.小明认为只要在适当时候前后轮胎交换使用,就可使这对轮胎能行驶最长路程.经过计算,小明算出,要使行驶路程最长,只需在行驶多少千公里时交换前后轮胎? 21教育网
参考答案
【基础训练】
1.【答案】B
解:大长方形的宽可以表示为(x+2y)厘米,宽又是75厘米,故x+2y=75,大长方形的长可以表示为2x厘米或(x+3y)厘米,故2x=3y+x,整理得x=3y,联立两个方程即可.www.21-cn-jy.com
2.【答案】A 3.【答案】D
4.【答案】52
5.解:设可以做成甲种盒子x个,乙种盒子y个,则
解得
答:可以做成甲种盒子30个,乙种盒子60个.
6.解:(1)设8座车租x辆,4座车租y辆,
则8x+4y=36,即2x+y=9,
∵x,y均为非负整数,∴x可取0,1,2,3,4,
则y依次为9,7,5,3,1,
则租车方案有:
8座车4辆,4座车1辆;
8座车3辆,4座车3辆;
8座车2辆,4座车5辆.(答案不唯一)
(2)∵8座车每个座的费用比4座车每个座的费用少,所以欲使费用最少,则必须多租8座车,
∴符合要求的租车方案为:8座车4辆,4座车1辆.
分析:任意一个二元一次方程都有无数个解,但具体问题要具体分析,如本题中未知数的解都应是非负整数.
【培优提升】
1.【答案】C
解:设笑脸气球x元一个,爱心气球y元一个,由题意,得∴3x+y+x+3y=14+18,即4x+4y=32,∴2x+2y=16.故选C.
2.【答案】36
解:设飞镖投到最小的圆中得x分,投到中间的圆环中得y分,投到最外面的圆环中得z分,根据题意得:解得:则小华的成绩是18+11+7=36(分).21世纪教育网版权所有
3.解:(1)2;3
(2)设应放入大球m个,小球n个.由题意,得
解得:
答:如果要使水面上升到50 cm,应放入大球4个,小球6个.
4.解:(1)由已知条件可得:解得:
(2)如图所示.
3
10
5
8
6
4
7
2
9
5.解:设每个新轮胎报废时的总磨损量为k,则安装在前轮的轮胎每行驶1千公里磨损量为,安装在后轮的轮胎每行驶1千公里的磨损量为.设一对新轮胎交换位置前走了x千公里,交换位置后走了y千公里.
两式相加得:+=2k,
解得x+y=9.6,
也就是一对新轮胎最多能行驶9.6千公里,再设在行了a千公里时互换前后轮胎,对一只轮胎而言,装在前轮上行了a千公里,装在后轮上就行了(9.6-a)千公里,根据题意可得方程21cnjy.com
+=k,解得:a=4.8.
答:要使行驶路程最长,只需在行驶4.8千公里时交换前后轮胎.
核心笔记: 列二元一次方程组解应用题的一般步骤:
(1)弄清题意和题目中的数量关系,用字母(如x、y、z)表示题目中的未知数;
(2)找出能够表达应用题全部含义的相等关系;
(3)根据这些相等关系列出需要的代数式,从而列出方程并组成方程组;
(4)解这个方程组,求出未知数的值;
(5)检验所得方程组的解是否正确和符合题目的实际意义,并写出答案(包括单位名称).
基础训练
1.如图,10块相同的长方形墙砖拼成一个大长方形,设长方形墙砖的长和宽分别为x厘米和y厘米,则依题意列方程组正确的是( )
A. B.
C. D.
2.一张方桌由一个桌面与四条桌腿组成,1 m3木料可以做桌面50个或桌腿300条,现有10 m3的木料,能恰好做成方桌多少张?设用x m3的木料做桌面,y m3的木料做桌腿,则满足以上关系的方程组是( )
A. B.
C. D.
3.如图,分别用火柴棍连续搭建正三角形和正六边形,公共边只用一根火柴棍.如果搭建正三角形和正六边形共用了2 016根火柴棍,并且正三角形的个数比正六边形的个数多6个,那么能连续搭建的正三角形的个数是( )21·cn·jy·com
A.222 B.280 C.286 D.292
4.一个两位数各数位上的数字之和是7,这个两位数减去27,它的十位和个位上的数字就交换了位置,则这个两位数是__________.
5.如图所示,某纸品厂为了制作甲、乙两种无盖的长方体盒子,利用边角料裁出了长方形和正方形两种硬纸片,长方形的宽与正方形的边长相等.现将150张正方形硬纸片和300张长方形硬纸片全部用于制作这两种盒子,可以做成甲、乙两种盒子各多少个?2·1·c·n·j·y
6.某球迷协会组织36名球迷拟租乘汽车赴比赛场地,为中国男子足球队呐喊助威,可利用的汽车有两种:一种每辆可乘8人,另一种每辆可乘4人,要求租用的汽车不留空座,也不超载. 【来源:21·世纪·教育·网】
(1)请你给出三种不同的租车方案;
(2)若8个座位的汽车租金是300元/天,4个座位的汽车租金是200元/天,请你设计费用最少的租车方案.21·世纪*教育网
培优提升
1.陈老师打算购买气球装扮学校六一儿童节活动会场,气球的种类有笑脸和爱心两种,两种气球的价格不同,但同一种气球的价格相同,由于会场布置需要,购买时以一束(4个气球)为单位,已知第一、二束气球的价格如图所示,则第三束气球的价格为( )www-2-1-cnjy-com
A.19元 B.18元 C.16元 D.15元
2.某校组织了一次游戏:每位选手朝特制的靶子上各投三次飞镖,在同一圆环内得分相同.如图所示,小明、小君、小红的成绩分别是29分、43分和33分,则小华的成绩是________分.2-1-c-n-j-y
3.根据图中给出的信息,解答下列问题:
(1)放入一个小球水面升高_____cm,放入一个大球水面升高_____cm;?
(2)如果要使水面上升到50 cm,应放入大球、小球各多少个?
4.如图,在3×3的方格内,填写了一些代数式.
(1)在图①中各行、各列及对角线上三个数之和都相等,请你求出x,y的值;
(2)把满足(1)的其他6个数填入图②中的方格内.
5
-3x
4
7
-x
3y
①
5
4
7
②
5.小明新买了一辆自行车,他在网上查找了相应型号自行车轮胎使用有关小知识,如图.小明认为只要在适当时候前后轮胎交换使用,就可使这对轮胎能行驶最长路程.经过计算,小明算出,要使行驶路程最长,只需在行驶多少千公里时交换前后轮胎? 21教育网
参考答案
【基础训练】
1.【答案】B
解:大长方形的宽可以表示为(x+2y)厘米,宽又是75厘米,故x+2y=75,大长方形的长可以表示为2x厘米或(x+3y)厘米,故2x=3y+x,整理得x=3y,联立两个方程即可.www.21-cn-jy.com
2.【答案】A 3.【答案】D
4.【答案】52
5.解:设可以做成甲种盒子x个,乙种盒子y个,则
解得
答:可以做成甲种盒子30个,乙种盒子60个.
6.解:(1)设8座车租x辆,4座车租y辆,
则8x+4y=36,即2x+y=9,
∵x,y均为非负整数,∴x可取0,1,2,3,4,
则y依次为9,7,5,3,1,
则租车方案有:
8座车4辆,4座车1辆;
8座车3辆,4座车3辆;
8座车2辆,4座车5辆.(答案不唯一)
(2)∵8座车每个座的费用比4座车每个座的费用少,所以欲使费用最少,则必须多租8座车,
∴符合要求的租车方案为:8座车4辆,4座车1辆.
分析:任意一个二元一次方程都有无数个解,但具体问题要具体分析,如本题中未知数的解都应是非负整数.
【培优提升】
1.【答案】C
解:设笑脸气球x元一个,爱心气球y元一个,由题意,得∴3x+y+x+3y=14+18,即4x+4y=32,∴2x+2y=16.故选C.
2.【答案】36
解:设飞镖投到最小的圆中得x分,投到中间的圆环中得y分,投到最外面的圆环中得z分,根据题意得:解得:则小华的成绩是18+11+7=36(分).21世纪教育网版权所有
3.解:(1)2;3
(2)设应放入大球m个,小球n个.由题意,得
解得:
答:如果要使水面上升到50 cm,应放入大球4个,小球6个.
4.解:(1)由已知条件可得:解得:
(2)如图所示.
3
10
5
8
6
4
7
2
9
5.解:设每个新轮胎报废时的总磨损量为k,则安装在前轮的轮胎每行驶1千公里磨损量为,安装在后轮的轮胎每行驶1千公里的磨损量为.设一对新轮胎交换位置前走了x千公里,交换位置后走了y千公里.
两式相加得:+=2k,
解得x+y=9.6,
也就是一对新轮胎最多能行驶9.6千公里,再设在行了a千公里时互换前后轮胎,对一只轮胎而言,装在前轮上行了a千公里,装在后轮上就行了(9.6-a)千公里,根据题意可得方程21cnjy.com
+=k,解得:a=4.8.
答:要使行驶路程最长,只需在行驶4.8千公里时交换前后轮胎.
