高中数学(人教)必修4:第二章《平面向量 》检测试卷A
文档属性
| 名称 | 高中数学(人教)必修4:第二章《平面向量 》检测试卷A |

|
|
| 格式 | zip | ||
| 文件大小 | 296.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-15 00:00:00 | ||
图片预览


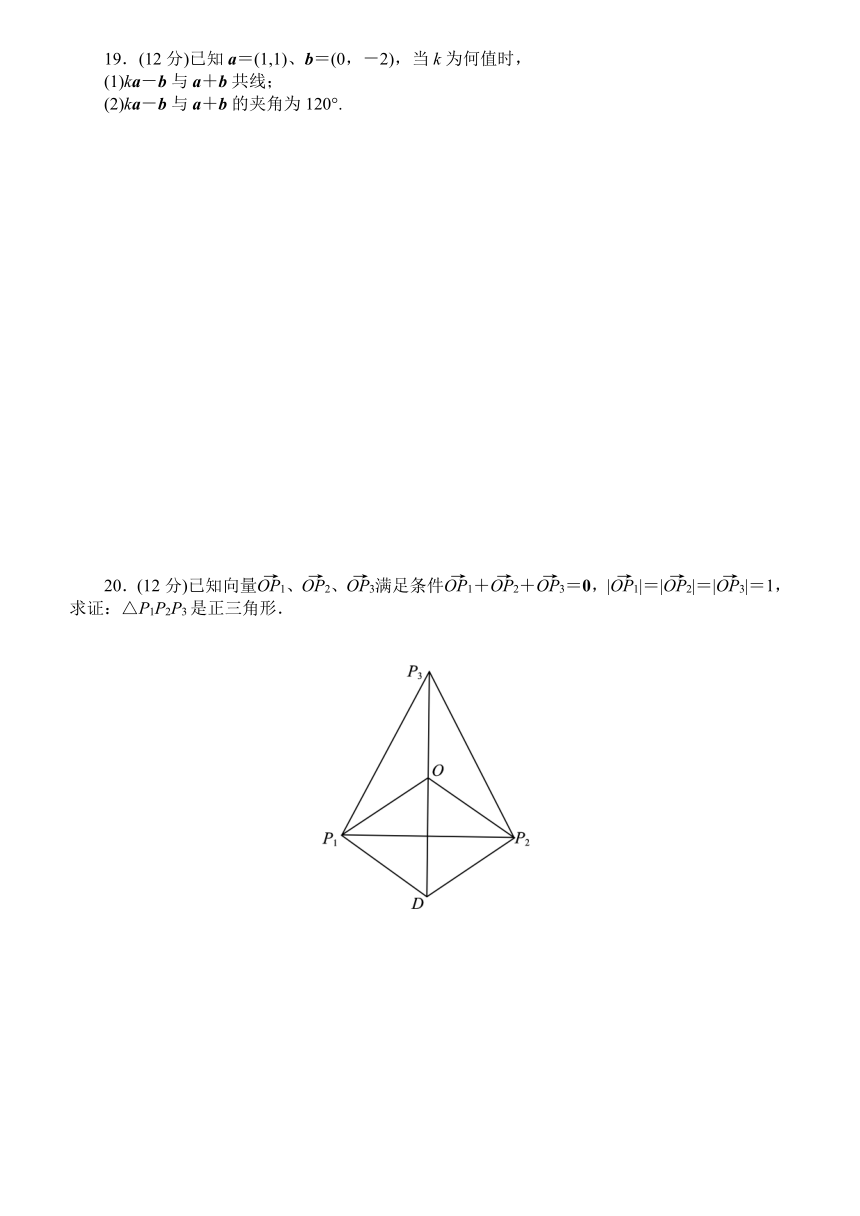

文档简介
高中数学(人教)必修4:第二章《平面向量
》检测试卷A
本试卷满分150分,考试时间120分钟.
一、选择题:本大题共12题,每题5分,共60分.在下列各题的四个选项中,只有一个选项是符合题目要求的.
1.下列各式叙述不正确的是( )
A.若a=λ
b,则a、b共线
B.若b=3a(a为非零向量),则a、b共线
C.若m=3a+4b,n=a-2b,则m∥n
D.若a+b+c=0,则a+b=-c
2.已知向量a,b和实数λ,下列选项中错误的是( )
A.|a|=
B.|a·
( http: / / www.21cnjy.com )b|=|a|·|b
|C.λ(a·b)=λa·b
D.|a·b|≤|a|·|b|
3.已知点A(1,3),B(4,-1),则与向量同方向的单位向量为( )
A.
B.
C.
D.
4.已知O是△ABC所在平面内一点,D为BC边的中点,且2++=0,那么( )
A.=
B.=2
C.=3
D.2=
5.若|a|=1,|b|=6,a·(b-a)=2,则a与b的夹角为( )
A.
B.
C.
D.
6.若四边形ABCD满足:+=0,(+)⊥,则该四边形一定是( )
A.矩形
B.菱形
C.正方形
D.直角梯形
7.给定两个向量a=(2,1),b=(-3,4),若(a+xb)⊥(a-b),则x等于( )
A.
B.
C.
D.
8.如图所示,在重600N的物体上拴两根绳子,与铅垂线的夹角分别为30°,60°,重物平衡时,两根绳子拉力的大小分别为( )
A.300
N,300
N
B.150N,150N
C.300
N,300N
D.300N,300N
9.已知向量a=(1,2),b=(-2,-4),|c|=,若(a+b)·c=,则a与c的夹角为( )
A.30°
B.60°
C.120°
D.150°
10.若向量=(1,-2),n=(1,3),且n·=6,则n·等于( )
A.-8
B.9
C.-10
D.11
11.在边长为1的正三角形ABC中,=,E是CA的中点,则·等于( )
A.-
B.-
C.-
D.-
12.已知|a|=2
,|b|=3,a,b的夹角为,如图所示,若=5a+2b,=a-3b,且D为BC中点,则的长度为( )
A.
B.
C.7
D.8
二、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中横线上.
13.已知向量a和向量b的夹角为30°,|a|=2,|b|=,则a·b=________.
14.已知a是平面内的单位向量,若向量b满足b·(a-b)=0,则|b|的取值范围是________.
15.设向量a与b的夹角为α,且a=(3,3),2b-a=(-1,1),则cosα=________.
16.关于平面向量a,b,c,有下列三个命题:
①若a·b=a·c,则b=c;②若a=(1
( http: / / www.21cnjy.com ),k),b=(-2,6),a∥b,则k=-3;③非零向量a和b满足|a|=|b|=|a-b|,则a与a+b的夹角为60°,其中真命题的序号为________.(写出所有真命题的序号)
三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)已知|a|=4,|b|=8,a与b的夹角是150°,计算:
(1)(a+2b)·(2a-b);
(2)|4a-2b|.
18.(12分)已知向量a=(-3,2),b=(2,1),c=(3,-1),t∈R,
(1)求|a+tb|的最小值及相应的t值;
(2)若a-tb与c共线,求实数t的值.
19.(12分)已知a=(1,1)、b=(0,-2),当k为何值时,
(1)ka-b与a+b共线;
(2)ka-b与a+b的夹角为120°.
20.(12分)已知向量、、满足条件++=0,||=||=||=1,求证:△P1P2P3是正三角形.
21.(12分)在平面直角坐标系xOy中,点A(-1,-2),B(2,3),C(-2,-1).
(1)求以线段AB,AC为邻边的平行四边形两条对角线的长;
(2)设实数t满足(-t)·=0,求t的值.
22.(12分)设集合D={平面向量},定义在D上的映射f满足:对任意x∈D,均有f(x)=λx(λ∈R且λ≠0).
(1)若|a|=|b|,且a、b不共线,试证明:[f(a)-f(b)]⊥(a+b);
(2)若A(1,2),B(3,6),C(4,8),且f()=,求f()·.
参考答案
一、答案:C
解析:根据共线向量定理及向量的线性运算易解.
2.答案:B
解析:|a·b|=|a|·|b||cosθ|,只有a与b共线时,才有|a·b|=|a||b|,可知B是错误的.
3.答案:A
解析:=(3,-4),则与其同方向的单位向量e==(3,-4)=.
4.答案:A
解析:由于2++=0,则+=-2=2.
所以(+)=,又D为BC边中点,
所以=(+).所以=.
5.答案:C
解析:a·(b-a)=a·b-a2=1×6×cosθ-1=2,cosθ=,θ∈[0,π],故θ=.
6.答案:B
解析:由+=0 ∥且||=||,即四边形ABCD是平行四边形,又(+)⊥ ⊥,所以四边形ABCD是菱形.
7.答案:D
解析:a+x
( http: / / www.21cnjy.com )b=(2,1)+(-3x,4x)=(2-3x,1+4x),a-b=(2,1)-(-3,4)=(5,-3),∵(a+xb)⊥(a-b),∴(2-3x)·5+(1+4x)·(-3)=0,∴x=.
8.答案:C
解析:如图:作 OACB,使∠AOC=30°,∠BOC=60°,∠OAC=90°,||=||cos30°=300
N.
|OB=||sin30°=300N.
9.答案:C
解析:由条件知|a|=,|b|=2,a+b=(-1,-2),∴|a+b|=,∵(a+b)·c=,∴×·cosθ=,其中θ为a+b与c的夹角,∴θ=60°,∵a+b=-a,∴a+b与a方向相反,∴a与c的夹角为120°.
10.答案:D
解析:n·=1-6=-5,n·=n·(+)=n·+n·=6,∴n·=11.
11.答案:A
解析:建立如图所示的直角坐标系,则
( http: / / www.21cnjy.com )A,B,C,依题意设D(x1,0),E(x2,y2),∵=,∴=(-1,0),∴x1=.
∵E是CA的中点,∴=,又=,∴x2=-,y2=.
∴·=·=×+×=-.故选A.
12.答案:A
解析:=(+)=(5a+2b+a-3b)=(6a-b)
∴||2=(36a2-12ab+b2)=.
∴||=.
二、13.答案:3
解析:a·b=2××=3.
14.答案:[0,1]
解析:∵
( http: / / www.21cnjy.com )b·(a-b)=0,∴a·b=b2,即|a||b|·cosθ=|b|2,当b≠0时,|b|=|a|cosθ=cosθ∈(0,1],所以|b|∈[0,1].
15.答案:
解析:设b=(x,y),则2b-a=(2x-3,2y-3)=
(-1,1),∴x=1,y=2,则b=(1,2),
cosα====.
16.答案:②
解析:①a与b的夹角为θ1,a与c的夹角为θ2.
a·b=a·c,
有|a||b|cosθ1=|a||c|cosθ2,得不到b=c,错误.
②a=(1,k),b=(-2,6),
∵a∥b,∴b=λa,得k=-3.正确.
③设|a|=|b|=|a-b|=m(m>0),
且a与a+b的夹角为θ.
则有(a-b)2=a2-2a·b+b2=m2,
∴2a·b=m2.
a·(a+b)=a2+a·b=m2+=,
(a+b)2=a2+2a·b+b2=m2+m2+m2=3m2,
∴cosθ===.
∴θ=30°.∴③错误.
三、17.解:(1)(a+2b)·(2a-b)
=2a2+3a·b-2b2
=2|a|2+3|a|·|b|·cos150°-2|b|2
=2×42+3×4×8×-2×82
=-96-48
.
(2)|4a-2b|=
=
=
=
=8(+)
18.解:(1)∵a=(-3,2),b=(2,1),c=(3,-1),
∴a+tb=(-3,2)+t(2,1)=(-3+2t,2+t),
∴|a+tb|=
=
=≥=,
当且仅当t=时取等号,即|a+tb|的最小值为,此时t=.
(2)∵a-tb=(-3-2t,2-t),
又a-tb与c共线,c=(3,-1),
∴(-3-2t)×(-1)-(2-t)×3=0,解得t=.
19.解:∵a=(1,1),b=(0,-2)
∵ka-b=k(1,1)-(0,-2)=(k,k+2)
a+b=(1,-1)
(1)要使ka-b与a+b共线,则-k-(k+2)=0,即k=-1.
(2)要使ka-b与a+b的夹角为120°,
∵|ka-b|=,
|a+b|=,
∴cos120°=
==-.
即k2+2k-2=0,解得k=-1±.
20.证明:如图所示,设=+,由于++=0,∴=-,||=1,
∴||=1=||,∴∠OP1P2=30°,
同理可得∠OP1P3=30°,∴∠P3P1P2=60°.
同理可得∠P2P3P1=60°,
∴△P1P2P3为正三角形.
21.解:(1)由题设知=(3,5),=(-1,1),则+=(2,6),-=(4,4),
所以|+|=2,|-|=4,故所求的两条对角线的长分别为4,2.
(2)由题设知=(-2,-1),-t=(3+2t,5+t).
由(-t)·=0,得(3+2t,5+t)·(-2,-1)=0,
即5t=-11,所以t=-.
22.解:(1)证明:∵f(a)-f(b)=λa-λb=λ(a-b),
∴[f(a)-f(b)]·(a+b)=λ(a-b)(a+b)=λ(a2-b2)=λ(|a|2-|b|2)=0,
∴[f(a)-f(b)]⊥(a+b).
(2)由已知得=(2,4),=(1,2),=(3,6).
∵f()=,∴λ=.
即λ(1,2)=(2,4),∴λ=2.
∴f()·=(2)·=(6,12)·(2,4)=60.
》检测试卷A
本试卷满分150分,考试时间120分钟.
一、选择题:本大题共12题,每题5分,共60分.在下列各题的四个选项中,只有一个选项是符合题目要求的.
1.下列各式叙述不正确的是( )
A.若a=λ
b,则a、b共线
B.若b=3a(a为非零向量),则a、b共线
C.若m=3a+4b,n=a-2b,则m∥n
D.若a+b+c=0,则a+b=-c
2.已知向量a,b和实数λ,下列选项中错误的是( )
A.|a|=
B.|a·
( http: / / www.21cnjy.com )b|=|a|·|b
|C.λ(a·b)=λa·b
D.|a·b|≤|a|·|b|
3.已知点A(1,3),B(4,-1),则与向量同方向的单位向量为( )
A.
B.
C.
D.
4.已知O是△ABC所在平面内一点,D为BC边的中点,且2++=0,那么( )
A.=
B.=2
C.=3
D.2=
5.若|a|=1,|b|=6,a·(b-a)=2,则a与b的夹角为( )
A.
B.
C.
D.
6.若四边形ABCD满足:+=0,(+)⊥,则该四边形一定是( )
A.矩形
B.菱形
C.正方形
D.直角梯形
7.给定两个向量a=(2,1),b=(-3,4),若(a+xb)⊥(a-b),则x等于( )
A.
B.
C.
D.
8.如图所示,在重600N的物体上拴两根绳子,与铅垂线的夹角分别为30°,60°,重物平衡时,两根绳子拉力的大小分别为( )
A.300
N,300
N
B.150N,150N
C.300
N,300N
D.300N,300N
9.已知向量a=(1,2),b=(-2,-4),|c|=,若(a+b)·c=,则a与c的夹角为( )
A.30°
B.60°
C.120°
D.150°
10.若向量=(1,-2),n=(1,3),且n·=6,则n·等于( )
A.-8
B.9
C.-10
D.11
11.在边长为1的正三角形ABC中,=,E是CA的中点,则·等于( )
A.-
B.-
C.-
D.-
12.已知|a|=2
,|b|=3,a,b的夹角为,如图所示,若=5a+2b,=a-3b,且D为BC中点,则的长度为( )
A.
B.
C.7
D.8
二、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中横线上.
13.已知向量a和向量b的夹角为30°,|a|=2,|b|=,则a·b=________.
14.已知a是平面内的单位向量,若向量b满足b·(a-b)=0,则|b|的取值范围是________.
15.设向量a与b的夹角为α,且a=(3,3),2b-a=(-1,1),则cosα=________.
16.关于平面向量a,b,c,有下列三个命题:
①若a·b=a·c,则b=c;②若a=(1
( http: / / www.21cnjy.com ),k),b=(-2,6),a∥b,则k=-3;③非零向量a和b满足|a|=|b|=|a-b|,则a与a+b的夹角为60°,其中真命题的序号为________.(写出所有真命题的序号)
三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)已知|a|=4,|b|=8,a与b的夹角是150°,计算:
(1)(a+2b)·(2a-b);
(2)|4a-2b|.
18.(12分)已知向量a=(-3,2),b=(2,1),c=(3,-1),t∈R,
(1)求|a+tb|的最小值及相应的t值;
(2)若a-tb与c共线,求实数t的值.
19.(12分)已知a=(1,1)、b=(0,-2),当k为何值时,
(1)ka-b与a+b共线;
(2)ka-b与a+b的夹角为120°.
20.(12分)已知向量、、满足条件++=0,||=||=||=1,求证:△P1P2P3是正三角形.
21.(12分)在平面直角坐标系xOy中,点A(-1,-2),B(2,3),C(-2,-1).
(1)求以线段AB,AC为邻边的平行四边形两条对角线的长;
(2)设实数t满足(-t)·=0,求t的值.
22.(12分)设集合D={平面向量},定义在D上的映射f满足:对任意x∈D,均有f(x)=λx(λ∈R且λ≠0).
(1)若|a|=|b|,且a、b不共线,试证明:[f(a)-f(b)]⊥(a+b);
(2)若A(1,2),B(3,6),C(4,8),且f()=,求f()·.
参考答案
一、答案:C
解析:根据共线向量定理及向量的线性运算易解.
2.答案:B
解析:|a·b|=|a|·|b||cosθ|,只有a与b共线时,才有|a·b|=|a||b|,可知B是错误的.
3.答案:A
解析:=(3,-4),则与其同方向的单位向量e==(3,-4)=.
4.答案:A
解析:由于2++=0,则+=-2=2.
所以(+)=,又D为BC边中点,
所以=(+).所以=.
5.答案:C
解析:a·(b-a)=a·b-a2=1×6×cosθ-1=2,cosθ=,θ∈[0,π],故θ=.
6.答案:B
解析:由+=0 ∥且||=||,即四边形ABCD是平行四边形,又(+)⊥ ⊥,所以四边形ABCD是菱形.
7.答案:D
解析:a+x
( http: / / www.21cnjy.com )b=(2,1)+(-3x,4x)=(2-3x,1+4x),a-b=(2,1)-(-3,4)=(5,-3),∵(a+xb)⊥(a-b),∴(2-3x)·5+(1+4x)·(-3)=0,∴x=.
8.答案:C
解析:如图:作 OACB,使∠AOC=30°,∠BOC=60°,∠OAC=90°,||=||cos30°=300
N.
|OB=||sin30°=300N.
9.答案:C
解析:由条件知|a|=,|b|=2,a+b=(-1,-2),∴|a+b|=,∵(a+b)·c=,∴×·cosθ=,其中θ为a+b与c的夹角,∴θ=60°,∵a+b=-a,∴a+b与a方向相反,∴a与c的夹角为120°.
10.答案:D
解析:n·=1-6=-5,n·=n·(+)=n·+n·=6,∴n·=11.
11.答案:A
解析:建立如图所示的直角坐标系,则
( http: / / www.21cnjy.com )A,B,C,依题意设D(x1,0),E(x2,y2),∵=,∴=(-1,0),∴x1=.
∵E是CA的中点,∴=,又=,∴x2=-,y2=.
∴·=·=×+×=-.故选A.
12.答案:A
解析:=(+)=(5a+2b+a-3b)=(6a-b)
∴||2=(36a2-12ab+b2)=.
∴||=.
二、13.答案:3
解析:a·b=2××=3.
14.答案:[0,1]
解析:∵
( http: / / www.21cnjy.com )b·(a-b)=0,∴a·b=b2,即|a||b|·cosθ=|b|2,当b≠0时,|b|=|a|cosθ=cosθ∈(0,1],所以|b|∈[0,1].
15.答案:
解析:设b=(x,y),则2b-a=(2x-3,2y-3)=
(-1,1),∴x=1,y=2,则b=(1,2),
cosα====.
16.答案:②
解析:①a与b的夹角为θ1,a与c的夹角为θ2.
a·b=a·c,
有|a||b|cosθ1=|a||c|cosθ2,得不到b=c,错误.
②a=(1,k),b=(-2,6),
∵a∥b,∴b=λa,得k=-3.正确.
③设|a|=|b|=|a-b|=m(m>0),
且a与a+b的夹角为θ.
则有(a-b)2=a2-2a·b+b2=m2,
∴2a·b=m2.
a·(a+b)=a2+a·b=m2+=,
(a+b)2=a2+2a·b+b2=m2+m2+m2=3m2,
∴cosθ===.
∴θ=30°.∴③错误.
三、17.解:(1)(a+2b)·(2a-b)
=2a2+3a·b-2b2
=2|a|2+3|a|·|b|·cos150°-2|b|2
=2×42+3×4×8×-2×82
=-96-48
.
(2)|4a-2b|=
=
=
=
=8(+)
18.解:(1)∵a=(-3,2),b=(2,1),c=(3,-1),
∴a+tb=(-3,2)+t(2,1)=(-3+2t,2+t),
∴|a+tb|=
=
=≥=,
当且仅当t=时取等号,即|a+tb|的最小值为,此时t=.
(2)∵a-tb=(-3-2t,2-t),
又a-tb与c共线,c=(3,-1),
∴(-3-2t)×(-1)-(2-t)×3=0,解得t=.
19.解:∵a=(1,1),b=(0,-2)
∵ka-b=k(1,1)-(0,-2)=(k,k+2)
a+b=(1,-1)
(1)要使ka-b与a+b共线,则-k-(k+2)=0,即k=-1.
(2)要使ka-b与a+b的夹角为120°,
∵|ka-b|=,
|a+b|=,
∴cos120°=
==-.
即k2+2k-2=0,解得k=-1±.
20.证明:如图所示,设=+,由于++=0,∴=-,||=1,
∴||=1=||,∴∠OP1P2=30°,
同理可得∠OP1P3=30°,∴∠P3P1P2=60°.
同理可得∠P2P3P1=60°,
∴△P1P2P3为正三角形.
21.解:(1)由题设知=(3,5),=(-1,1),则+=(2,6),-=(4,4),
所以|+|=2,|-|=4,故所求的两条对角线的长分别为4,2.
(2)由题设知=(-2,-1),-t=(3+2t,5+t).
由(-t)·=0,得(3+2t,5+t)·(-2,-1)=0,
即5t=-11,所以t=-.
22.解:(1)证明:∵f(a)-f(b)=λa-λb=λ(a-b),
∴[f(a)-f(b)]·(a+b)=λ(a-b)(a+b)=λ(a2-b2)=λ(|a|2-|b|2)=0,
∴[f(a)-f(b)]⊥(a+b).
(2)由已知得=(2,4),=(1,2),=(3,6).
∵f()=,∴λ=.
即λ(1,2)=(2,4),∴λ=2.
∴f()·=(2)·=(6,12)·(2,4)=60.
