福建省厦门市2016-2017学年高二(上)期末数学试卷(文科)(解析版)
文档属性
| 名称 | 福建省厦门市2016-2017学年高二(上)期末数学试卷(文科)(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 268.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-16 07:32:50 | ||
图片预览




文档简介
2016-2017学年福建省厦门市高二(上)期末数学试卷(文科)
一、选择题(共12小题,每小题5分,满分60分)
1.已知{an}是等比数列,a1=2,a4=16,则数列{an}的公比q等于( )
A.2
B.﹣2
C.
D.﹣
2.设x∈R,则“x>1“是“x3>1”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
3.已知抛物线y2=12x上一点M到焦点的距离为8,则点M的横坐标为( )
A.2
B.3
C.4
D.5
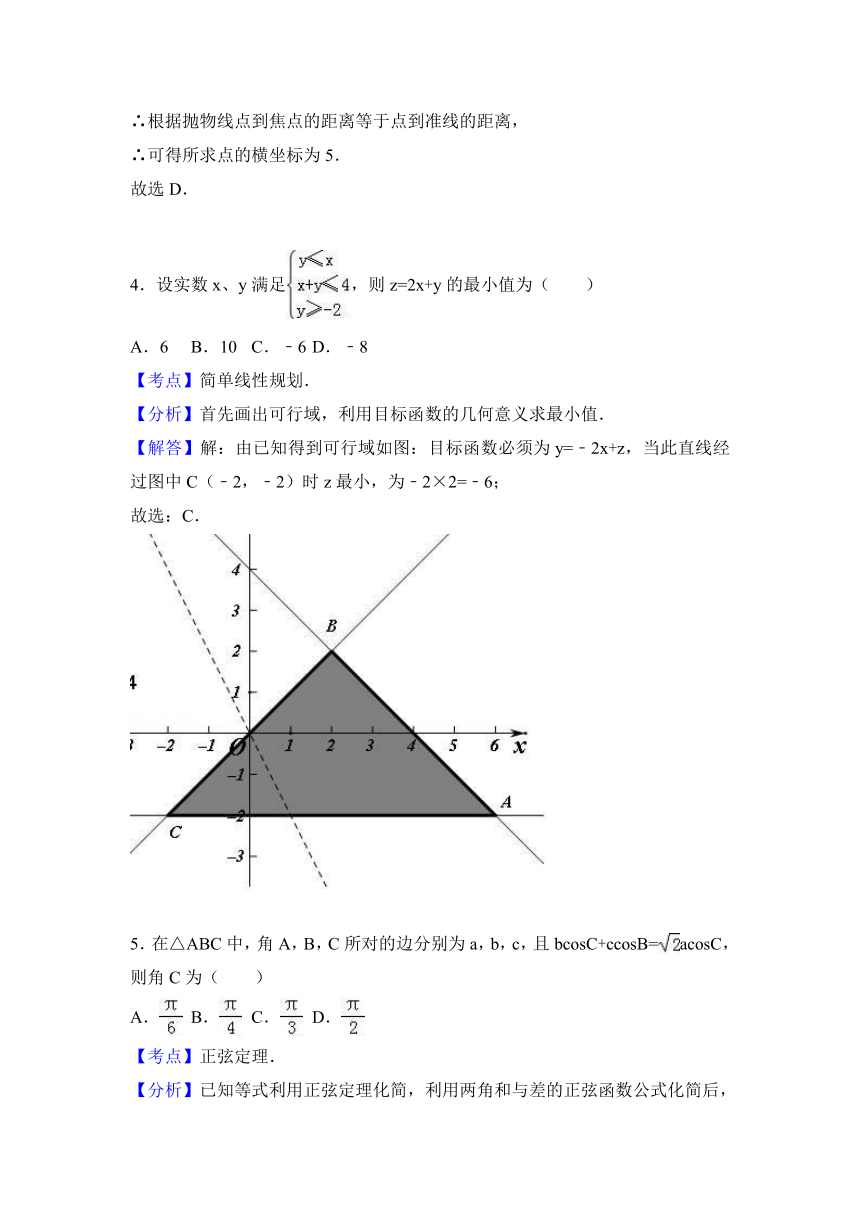
4.设实数x、y满足,则z=2x+y的最小值为( )
A.6
B.10
C.﹣6
D.﹣8
5.在△ABC中,角A,B,C所对的边分别为a,b,c,且bcosC+ccosB=acosC,则角C为( )
A.
B.
C.
D.
6.已知{an}是等差数列,a1=﹣26,a8+a13=5,当{an}的前n项和Sn取最小值时,n等于( )
A.8
B.9
C.10
D.11
7.若双曲线=1(a>0,b>0)的一个焦点到一条渐近线的距离等于焦距的,则该双曲线的渐近线方程是( )
A.x±2y=0
B.2x±y=0
C.
x±y=0
D.xy=0
8.已知{an}是等比数列,{bn}是等差数列,若a2 a14=4a8,b8=a8,则数列{bn}的前15项和等于( )
A.30
B.40
C.60
D.120
9.若关于x的一元二次方程x2+ax﹣2=0有两个不相等的实根x1,x2,且x1<﹣1,x2>1,则实数a的取值范围是( )
A.a<﹣1
B.a>1
C.﹣1<a<1
D.a>2或a<﹣2
10.在△ABC中,角A,B,C所对的边分别为a,b,c,且a,2b,c成等比数列,则cosB的最小值为( )
A.
B.
C.
D.
11.已知函数f(x)=e2x﹣t,g(x)=tex﹣1,对任意x∈R,f(x)≥g(x)恒成立,则实数t的取值范围为( )
A.t≤1
B.t≤2﹣2
C.t≤2
D.t≤2﹣3
12.从一块短轴成为2m的椭圆形板材中截取一块面积最大的矩形,若椭圆的离心率为e,且e∈[,],则该矩形面积的取值范围是( )
A.[m2,2m2]
B.[2m2,3m2]
C.[3m2,4m2]
D.[4m2,5m2]
二、填空题(本大题共有4小题,每小题5分,共20分)
13.命题p: x∈R,ex≥1,写出命题p的否定: .
14.已知方程+=1表示焦点在x轴上的椭圆,则实数m的取值范围为 .
15.已知函数f(x)=,若an=f(n)(n∈N
),则数列{an}的前50项和等于 .
16.一个三角形三边是连续的三个自然数,且最大角是最小角的2倍,则这个三角形的周长等于 .
三、解答题(本大题共有6小题,共70分)
17.关于x的不等式x2﹣ax+b<0的解集为{x|2<x<3}.
(Ⅰ)求a+b;
(Ⅱ)若不等式﹣x2+bx+c>0的解集为空集,求c的取值范围.
18.如图,在梯形ABCD中,AB∥CD,∠DAC=30°,∠CAB=45°,CD=﹣.
(Ⅰ)求AD的长;
(Ⅱ)若BC=,求△ABC的面积.
19.已知数列{an}满足a5=13,an+1﹣an=3(n∈N
),数列{bn}的前n项和Sn=1﹣(n∈N
).
(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)记Tn=a1b1+a2b2+a3b3+…+anbn,比较Tn与4的大小.
20.已知直线l与抛物线y2=﹣x相交于A,B两点.A,B在准线上的摄影分别为A1,B1.
(Ⅰ)若线段AB的中点坐标为(﹣4,1),求直线l的方程;
(Ⅱ)若直线l方程为x=my﹣1,m∈R,求梯形AA1B1B的面积(用m表示).
21.某公司要招聘甲、乙两类员工共150
( http: / / www.21cnjy.com )人,该公司员工的工资由基础工资组成.其中甲、乙两类员工每人每月的基础工资分别为2千元和3千元,甲类员工每月的人均绩效工资与公司月利润成正比,比例系数为a(a>0),乙类员工每月的绩效工资与公司月利润的平方成正比,比例系数为b(b>0).
(Ⅰ)若要求甲类员工的人数不超过乙类员工人数的2倍,问甲、乙两类员工各招聘多少人时,公司每月所付基础工资总额最少?
(Ⅱ)若该公司每月的利润为x(x>0)千元
( http: / / www.21cnjy.com ),记甲、乙两类员工该月人均工资分别为w甲千元和w乙千元,试比较w甲和w乙的大小.(月工资=月基础工资+月绩效工资)
22.在圆O:x2+y2=4上任取一点P,过点P作y轴额垂线段PQ,Q为垂足.当P在圆上运动时,线段PQ中点G的轨迹为C.
(Ⅰ)求C的方程;
(Ⅱ)直线l与圆O交于M,N两点,与曲线C交于E,F两点,若|MN|=,试判断∠EOF是否为定值?若是,求出该定值;若不是,说明理由.
2016-2017学年福建省厦门市高二(上)期末数学试卷(文科)
参考答案与试题解析
一、选择题(共12小题,每小题5分,满分60分)
1.已知{an}是等比数列,a1=2,a4=16,则数列{an}的公比q等于( )
A.2
B.﹣2
C.
D.﹣
【考点】等比数列的通项公式.
【分析】利用等比数列的通项公式即可得出.
【解答】解:由等比数列的性质可得:a4=,∴16=2q3,解得q=2.
故选:A.
2.设x∈R,则“x>1“是“x3>1”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
【考点】必要条件、充分条件与充要条件的判断.
【分析】利用充要条件的判断方法判断选项即可.
【解答】解:因为x∈R,“x>1“ “x3>1”,
所以“x>1“是“x3>1”的充要条件.
故选:C.
3.已知抛物线y2=12x上一点M到焦点的距离为8,则点M的横坐标为( )
A.2
B.3
C.4
D.5
【考点】抛物线的简单性质.
【分析】根据抛物线点到焦点的距离等于点到准线的距离,可得所求点的横坐标.
【解答】解:抛物线y2=12x的准线方程为x=﹣3,
∵抛物线y2=12x上点到焦点的距离等于8,
∴根据抛物线点到焦点的距离等于点到准线的距离,
∴可得所求点的横坐标为5.
故选D.
4.设实数x、y满足,则z=2x+y的最小值为( )
A.6
B.10
C.﹣6
D.﹣8
【考点】简单线性规划.
【分析】首先画出可行域,利用目标函数的几何意义求最小值.
【解答】解:由已知得到可行域如图:目标函数必须为y=﹣2x+z,当此直线经过图中C(﹣2,﹣2)时z最小,为﹣2×2=﹣6;
故选:C.
5.在△ABC中,角A,B,C所对的边分别为a,b,c,且bcosC+ccosB=acosC,则角C为( )
A.
B.
C.
D.
【考点】正弦定理.
【分析】已知等式利用正弦定理化简,利用两角和与差的正弦函数公式化简后,根据sinA不为0,求出cosC的值,即可确定出C的度数.
【解答】解:已知等式利用正弦定理化简得:sinBcosC+sinCcosB=sinAcosC,
即sin(B+C)=sinAcosC,
变形得:sinA=sinAcosC,
∵sinA≠0,
∴cosC=,
∴由C∈(0,π),可得∠C=.
故选:B.
6.已知{an}是等差数列,a1=﹣26,a8+a13=5,当{an}的前n项和Sn取最小值时,n等于( )
A.8
B.9
C.10
D.11
【考点】等差数列的前n项和.
【分析】利用等差数列的通项公式先求出公差,再求出等差数列前n项和公式,由此利用配方法能求出{an}的前n项和Sn取最小值时,n的值.
【解答】解:∵{an}是等差数列,a1=﹣26,a8+a13=5,
∴﹣26+7d﹣26+12d=5,
解得d=3,
∴Sn=﹣26n+==(n﹣)2+,
∴{an}的前n项和Sn取最小值时,n=9.
故选:B.
7.若双曲线=1(a>0,b>0)的一个焦点到一条渐近线的距离等于焦距的,则该双曲线的渐近线方程是( )
A.x±2y=0
B.2x±y=0
C.
x±y=0
D.xy=0
【考点】双曲线的简单性质.
【分析】由题设知b=×2c,因此b=c,a=c,所以=,由此可求出其渐近线方程.
【解答】解:对于双曲线=1(a>0,b>0)的一个焦点到一条渐近线的距离为=b,
所以b=×2c,
因此b=c,a=c,
所以=
因此其渐近线方程为x±y=0.
故选:D.
8.已知{an}是等比数列,{bn}是等差数列,若a2 a14=4a8,b8=a8,则数列{bn}的前15项和等于( )
A.30
B.40
C.60
D.120
【考点】等差数列的前n项和.
【分析】由等比数列通项公式求出b8=a8=4,由此利用等差数列前n项和公式能求出数列{bn}的前15项和.
【解答】解:∵{an}是等比数列,{bn}是等差数列,a2 a14=4a8,b8=a8,
∴=4a8,解得b8=a8=4,
∴数列{bn}的前15项和为:
S15=(b1+b15)=15b8=15×4=60.
故选:C.
9.若关于x的一元二次方程x2+ax﹣2=0有两个不相等的实根x1,x2,且x1<﹣1,x2>1,则实数a的取值范围是( )
A.a<﹣1
B.a>1
C.﹣1<a<1
D.a>2或a<﹣2
【考点】一元二次方程的根的分布与系数的关系.
【分析】由题意设f(x)=x2+ax﹣2,由条件、函数与方程的关系、一元二次函数的图象列出不等式,求出实数a的取值范围.
【解答】解:由题意设f(x)=x2+ax﹣2,
∵方程x2+ax﹣2=0有两个不相等的实根x1,x2,
且x1<﹣1,x2>1,
∴,则,
解得﹣1<a<1,
故选:C.
10.在△ABC中,角A,B,C所对的边分别为a,b,c,且a,2b,c成等比数列,则cosB的最小值为( )
A.
B.
C.
D.
【考点】等比数列的通项公式.
【分析】由a,2b,c成等比数列,知4b2=ac,由此利用余弦定理和基本不等式能求出cosB的最小值.
【解答】解:∵a,2b,c成等比数列,∴4b2=ac,
∴cosB==﹣≥1﹣=.
当且仅当a=c时,取等号,
∴cosB的最小值为.
故选:D.
11.已知函数f(x)=e2x﹣t,g(x)=tex﹣1,对任意x∈R,f(x)≥g(x)恒成立,则实数t的取值范围为( )
A.t≤1
B.t≤2﹣2
C.t≤2
D.t≤2﹣3
【考点】函数恒成立问题.
【分析】设F(x)=f(x)﹣g(x),则
( http: / / www.21cnjy.com )F(x)=f(x)﹣g(x)=e2x﹣tex+1﹣t对任意x∈R,最小值为0,由此能求出实数t的取值范围.
【解答】解:设F(x)=f(x)﹣g(x),
∵函数f(x)=e2x﹣t,g(x)=tex﹣1,对任意x∈R,f(x)≥g(x)恒成立,
∴F(x)=f(x)﹣g(x)=e2x﹣tex+1﹣t对任意x∈R,最小值为0,
F′(x)=2e2x﹣tex,由F′(x)=0,得x=ln,
∴F(ln)=﹣te+1﹣t≥0,
整理,得t2+4t﹣4≤0,
解得﹣2﹣2<t<2﹣2.
故选:B.
12.从一块短轴成为2m的椭圆形板材中截取一块面积最大的矩形,若椭圆的离心率为e,且e∈[,],则该矩形面积的取值范围是( )
A.[m2,2m2]
B.[2m2,3m2]
C.[3m2,4m2]
D.[4m2,5m2]
【考点】椭圆的简单性质.
【分析】在第一象限内取点(
( http: / / www.21cnjy.com )x,y),设x=acosθ,y=bsinθ,表示出圆的内接矩形长和宽,可得矩形的面积,由e∈[,],∴ 2b≤a≤,得:4b2≤2ab≤5b2即可
【解答】解:在第一象限内取点(x,y),设x=acosθ,y=bsinθ,(0<θ<)
则椭圆的内接矩形长为2acosθ,宽为2bsinθ,
内接矩形面积为2acosθ 2bsinθ=2absin2θ≤2ab,
椭圆的离心率为e,且e∈[,],∴ 2b≤a≤,
得:4b2≤2ab≤5b2,矩形面积的取值范围是[4m2,5m2].
故选:D.
二、填空题(本大题共有4小题,每小题5分,共20分)
13.命题p: x∈R,ex≥1,写出命题p的否定: x∈R,ex<1 .
【考点】命题的否定.
【分析】本题中的命题是一个全称命题,其否定是特称命题,依据全称命题的否定书写形式写出命题的否定即可
【解答】解:∵命题p: x∈R,ex≥1,
∴命题p的否定是“ x∈R,ex<1”
故答案为: x∈R,ex<1
14.已知方程+=1表示焦点在x轴上的椭圆,则实数m的取值范围为 ﹣<m<1 .
【考点】椭圆的简单性质.
【分析】根据题意,由椭圆的标准方程分析可得,解可得m的取值范围,即可得答案.
【解答】解:根据题意,方程+=1表示焦点在x轴上的椭圆,
则必有,
解可得:﹣<m<1,
即m的取值范围是﹣<m<1,
故答案为:﹣<m<1.
15.已知函数f(x)=,若an=f(n)(n∈N
),则数列{an}的前50项和等于 .
【考点】数列的求和.
【分析】n≤7时,an=f(n)=2n
( http: / / www.21cnjy.com )﹣10,可得a6=f(6),a7=f(7).x>7时,a8=f(8)=,a9=f(9)=,n≥10时,an=f(n)==f(n﹣4).即可得出.
【解答】解:n≤7时,an=f(n)=2n﹣10,
∴a6=f(6)=2×6﹣10=2,a7=f(7)=2×7﹣10=4.
n>7时,a8=f(8)==,a9=f(9)==,a10=f(10)==f(6)=2,a11=f(11)==f(7)=4,
a12=f(12)==f(8)=,…,n≥10时,an=f(n)==f(n﹣4).
∴数列{an}的前50项和为:
+11×=.
故答案为:.
16.一个三角形三边是连续的三个自然数,且最大角是最小角的2倍,则这个三角形的周长等于 15 .
【考点】余弦定理;正弦定理.
【分析】设三角形三边是连续的三个自
( http: / / www.21cnjy.com )然n﹣1,n,n+1,三个角分别为α,π﹣3α,2α,由正弦定理求得cosα=,再由余弦定理可得
(n﹣1)2=(n+1)2+n2﹣2(n+1)n ,求得n=5,从而得出结论.
【解答】解:设三边长分别为n﹣1,n,n+1,对应的角为A,B,C,
由题意知C=2A,
由正弦定理得=
即有cosA=,
又cosA==
所以=,
化简为n2﹣5n=0,解得n=5,
所以三边分别为4,5,6,其周长=4+5+6=15.
故答案为:15.
三、解答题(本大题共有6小题,共70分)
17.关于x的不等式x2﹣ax+b<0的解集为{x|2<x<3}.
(Ⅰ)求a+b;
(Ⅱ)若不等式﹣x2+bx+c>0的解集为空集,求c的取值范围.
【考点】一元二次不等式的解法.
【分析】(Ⅰ)根据一元二次不等式与对应方程的关系,利用根与系数的关系求出a、b的值,再求和;
(Ⅱ)把b=6代入不等式﹣x2+bx+c>0,由判别式△≤0求出c的取值范围.
【解答】解:(Ⅰ)由题意得:方程x2﹣ax+b=0的两根为2和3,…
所以,
解得,…
所以a+b=11;
…
(Ⅱ)由(Ⅰ)知b=6,
因为不等式﹣x2+bx+c>0的解集为空集,
所以△=62+4c≤0,…
解得c≤﹣9,
所以c的取值范围为(﹣∞,﹣9].
…
18.如图,在梯形ABCD中,AB∥CD,∠DAC=30°,∠CAB=45°,CD=﹣.
(Ⅰ)求AD的长;
(Ⅱ)若BC=,求△ABC的面积.
【考点】正弦定理.
【分析】(Ⅰ)由已知可求∠DCA=∠CAB=45°,进而利用正弦定理可求AD的值.
(Ⅱ)利用两角和的正弦函数公式可求sin∠ADC,利用正弦定理可求AC,由余弦定理可求AB,进而利用三角形面积公式即可计算得解.
【解答】(本题满分为12分)
解:(Ⅰ)因为AB∥CD,
所以∠DCA=∠CAB=45°,…
因为,…
所以AD==2﹣2.
…
(Ⅱ)∠ADC=180°﹣(30°+45°)=105°,
所以,sin∠ADC=sin(45°+60°)=sin45°cos60°+cos45°sin60°=,…
因为=,
所以AC=2,…
设AB=x,
因为,BC2=AC2+AB2﹣2AC ABcos∠CAB,
可得:x2﹣2x﹣6=0,
所以,AB=3,….
所以,S△ABC=AC ABsin∠CAB=3.
…
19.已知数列{an}满足a5=13,an+1﹣an=3(n∈N
),数列{bn}的前n项和Sn=1﹣(n∈N
).
(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)记Tn=a1b1+a2b2+a3b3+…+anbn,比较Tn与4的大小.
【考点】数列的求和;数列递推式.
【分析】(I)利用等差数列的通项公式可得an.利用数列递推关系可得bn.
(II)利用“错位相减法”与等比数列的求和公式即可得出.
【解答】解:(Ⅰ)∵an+1﹣an=3(n∈N
),∴数列{an}为等差数列,公差d=3,
又a5=a1+4d=13,得a1=1,∴an=1+3(n﹣1)=3n﹣2.
又因为数列{bn}的前n项和为Sn=1﹣(n∈N
).,
当n=1时,b1=S1=,
当n≥2时,bn=Sn﹣Sn﹣1=1﹣﹣=.,
∴bn=.
综上:an=3n﹣2,bn=.
(Ⅱ)anbn=(3n﹣2).
Tn=1×+7×+…+(3n﹣2)×,
=+…+(3n﹣5)×+(3n﹣2)×,
得:
=﹣(3n﹣2)×=﹣(3n﹣2)×,
∴Tn=1+3﹣(3n﹣2)×=4﹣<4.
20.已知直线l与抛物线y2=﹣x相交于A,B两点.A,B在准线上的摄影分别为A1,B1.
(Ⅰ)若线段AB的中点坐标为(﹣4,1),求直线l的方程;
(Ⅱ)若直线l方程为x=my﹣1,m∈R,求梯形AA1B1B的面积(用m表示).
【考点】抛物线的简单性质.
【分析】(Ⅰ)分类讨论,利用线段AB的中点坐标为(﹣4,1),设出直线方程,利用韦达定理,求出k,即可求直线l的方程;
(Ⅱ)若直线l方程为x=my﹣1,m∈R,求出上底、下底、高,即可求梯形AA1B1B的面积(用m表示).
【解答】解:(Ⅰ)当直线l斜率不存在时,直线l方程为:x=﹣4,此时AB中点坐标为(﹣4,0),不符合题意
….
当直线l斜率存在时,因为直线与抛物线交于两不同点,所以斜率不为0,
设直线l方程为:y﹣1=k(x+4),即y=kx+4k+1(k≠0),
代入抛物线方程得:k2x2+(8k2+2k+1)x+(4k+1)2=0…
设A(x1,y1),B(x2,y2),因为A,B中点坐标为(﹣4,1),所以x1+x2=﹣8,
所以=﹣8,得k=﹣…
直线l的方程为y﹣1=﹣(x+4),即x+2y+2=0…
(Ⅱ)联立x=my﹣1与抛物线方程得:y2+my﹣1=0.
所以y1+y2=﹣m,y1y2=﹣1
…..
又|AA1|=﹣x1+=﹣my1+,|BB1|=﹣x2+=﹣my2+,
所以|AA1|+|BB1|=﹣my1+﹣my2+=m2+
|A1B1|=|y1﹣y2|=,
∴梯形AA1B1B的面积S=…..
21.某公司要招聘甲、乙两类员工共
( http: / / www.21cnjy.com )150人,该公司员工的工资由基础工资组成.其中甲、乙两类员工每人每月的基础工资分别为2千元和3千元,甲类员工每月的人均绩效工资与公司月利润成正比,比例系数为a(a>0),乙类员工每月的绩效工资与公司月利润的平方成正比,比例系数为b(b>0).
(Ⅰ)若要求甲类员工的人数不超过乙类员工人数的2倍,问甲、乙两类员工各招聘多少人时,公司每月所付基础工资总额最少?
(Ⅱ)若该公司每月的利润为x(x>0)千元,
( http: / / www.21cnjy.com )记甲、乙两类员工该月人均工资分别为w甲千元和w乙千元,试比较w甲和w乙的大小.(月工资=月基础工资+月绩效工资)
【考点】函数模型的选择与应用.
【分析】(Ⅰ)设招聘甲类员工人数为x,乙类员工人数为,求出公司每月所付的基础工资总额,即可得出结论;
(Ⅱ)由已知,w甲=2+a
( http: / / www.21cnjy.com )x,w乙=3+bx2,w乙﹣w甲=(3+bx2)﹣(2+ax)=bx2﹣ax+1(a>0,b>0,x>0),分类讨论,可得结论.
【解答】解:(Ⅰ)设招聘甲类员工人数为x,乙类员工人数为,公司每月所付的基础工资总额为y千元,
因为x≤2,所以0<x≤100,x∈N…
因为y=2x+3=450﹣x…
x=100时,ymin=350,
所以甲类员工招聘100人,乙类员工招聘50人
时,公司每月所付的基础工资
总额最少为
350000元…
(Ⅱ)由已知,w甲=2+ax,w乙=3+bx2…
w乙﹣w甲=(3+bx2)﹣(2+ax)=bx2﹣ax+1(a>0,b>0,x>0)…
△=a2﹣4b
(
i)当△<0,即a2<4b时,bx2﹣ax+1=0无实数根,
此时w乙﹣w甲>0,即w乙>w甲;…
(
ii)当△=0,即a2=4b时,bx2﹣ax+1=0有两个相等正实根,
①当x=时,w乙=w甲;…
②当x>0且x≠时,w乙>w甲;…
(
iii)当△>0,即a2>4b时,bx2﹣ax+1=0有两个不相等正数根和,
①当x∈(0,)∪(,+∞)时,w乙>w甲;…
②当x∈(,)时,w乙<w甲;…
③当x=或时,w乙=w甲…
22.在圆O:x2+y2=4上任取一点P,过点P作y轴额垂线段PQ,Q为垂足.当P在圆上运动时,线段PQ中点G的轨迹为C.
(Ⅰ)求C的方程;
(Ⅱ)直线l与圆O交于M,N两点,与曲线C交于E,F两点,若|MN|=,试判断∠EOF是否为定值?若是,求出该定值;若不是,说明理由.
【考点】直线与椭圆的位置关系;轨迹方程.
【分析】(Ⅰ)设G(x,
( http: / / www.21cnjy.com )y),P(x0,y0),所以Q(0,y0),由中点坐标公式得x0=2x,y0=y,由P(x0,y0)在圆O上,能求出C的方程.
(Ⅱ)求出点O到直线l的距离d=,当直线l斜率不存在时,∠EOF=90°;当直线l斜率存在时,设直线l:y=kx+m,求出5m2=4(k2+1),由得:(4+k2)x2+2mkx+m2﹣4=0,由此利用根的判别式、韦达定理,向量数量积求出∠EOF=90°.由此得到∠EOF=90°为定值.
【解答】解:(Ⅰ)设G(x,y),P(x0,y0),所以Q(0,y0),…
因为点G是线段PQ中点,所以x0=2x,y0=y,…..…..…
又P(x0,y0)在圆O上,所以(2x)2+y2=4,
即C的方程为:.…
(Ⅱ)设点O到直线l的距离为d,则d===,…
当直线l斜率不存在时,直线l方程:x=±,代入椭圆方程得:y=,
不妨设E(),F(,﹣),此时∠EOF=90°,…
当直线l斜率存在时,设直线l:y=kx+m,得kx﹣y+m=0,
所以d==,所以5m2=4(k2+1),…
由得:(4+k2)x2+2mkx+m2﹣4=0,…
(k2+16)>0,
设E(x1,y1),F(x2,y2),所以,,
=x1x2+y1y2=x1x2+(kx1+m)(kx2+m)=(1+k2)x1x2+mk(x1+x2)+m2
=(1+k2)+mk+m2=,…
把5m2=4(k2+1)代入上式得:
=0,所以OE⊥OF,即∠EOF=90°.
综上所述∠EOF=90°为定值.…
2017年3月14日
一、选择题(共12小题,每小题5分,满分60分)
1.已知{an}是等比数列,a1=2,a4=16,则数列{an}的公比q等于( )
A.2
B.﹣2
C.
D.﹣
2.设x∈R,则“x>1“是“x3>1”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
3.已知抛物线y2=12x上一点M到焦点的距离为8,则点M的横坐标为( )
A.2
B.3
C.4
D.5
4.设实数x、y满足,则z=2x+y的最小值为( )
A.6
B.10
C.﹣6
D.﹣8
5.在△ABC中,角A,B,C所对的边分别为a,b,c,且bcosC+ccosB=acosC,则角C为( )
A.
B.
C.
D.
6.已知{an}是等差数列,a1=﹣26,a8+a13=5,当{an}的前n项和Sn取最小值时,n等于( )
A.8
B.9
C.10
D.11
7.若双曲线=1(a>0,b>0)的一个焦点到一条渐近线的距离等于焦距的,则该双曲线的渐近线方程是( )
A.x±2y=0
B.2x±y=0
C.
x±y=0
D.xy=0
8.已知{an}是等比数列,{bn}是等差数列,若a2 a14=4a8,b8=a8,则数列{bn}的前15项和等于( )
A.30
B.40
C.60
D.120
9.若关于x的一元二次方程x2+ax﹣2=0有两个不相等的实根x1,x2,且x1<﹣1,x2>1,则实数a的取值范围是( )
A.a<﹣1
B.a>1
C.﹣1<a<1
D.a>2或a<﹣2
10.在△ABC中,角A,B,C所对的边分别为a,b,c,且a,2b,c成等比数列,则cosB的最小值为( )
A.
B.
C.
D.
11.已知函数f(x)=e2x﹣t,g(x)=tex﹣1,对任意x∈R,f(x)≥g(x)恒成立,则实数t的取值范围为( )
A.t≤1
B.t≤2﹣2
C.t≤2
D.t≤2﹣3
12.从一块短轴成为2m的椭圆形板材中截取一块面积最大的矩形,若椭圆的离心率为e,且e∈[,],则该矩形面积的取值范围是( )
A.[m2,2m2]
B.[2m2,3m2]
C.[3m2,4m2]
D.[4m2,5m2]
二、填空题(本大题共有4小题,每小题5分,共20分)
13.命题p: x∈R,ex≥1,写出命题p的否定: .
14.已知方程+=1表示焦点在x轴上的椭圆,则实数m的取值范围为 .
15.已知函数f(x)=,若an=f(n)(n∈N
),则数列{an}的前50项和等于 .
16.一个三角形三边是连续的三个自然数,且最大角是最小角的2倍,则这个三角形的周长等于 .
三、解答题(本大题共有6小题,共70分)
17.关于x的不等式x2﹣ax+b<0的解集为{x|2<x<3}.
(Ⅰ)求a+b;
(Ⅱ)若不等式﹣x2+bx+c>0的解集为空集,求c的取值范围.
18.如图,在梯形ABCD中,AB∥CD,∠DAC=30°,∠CAB=45°,CD=﹣.
(Ⅰ)求AD的长;
(Ⅱ)若BC=,求△ABC的面积.
19.已知数列{an}满足a5=13,an+1﹣an=3(n∈N
),数列{bn}的前n项和Sn=1﹣(n∈N
).
(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)记Tn=a1b1+a2b2+a3b3+…+anbn,比较Tn与4的大小.
20.已知直线l与抛物线y2=﹣x相交于A,B两点.A,B在准线上的摄影分别为A1,B1.
(Ⅰ)若线段AB的中点坐标为(﹣4,1),求直线l的方程;
(Ⅱ)若直线l方程为x=my﹣1,m∈R,求梯形AA1B1B的面积(用m表示).
21.某公司要招聘甲、乙两类员工共150
( http: / / www.21cnjy.com )人,该公司员工的工资由基础工资组成.其中甲、乙两类员工每人每月的基础工资分别为2千元和3千元,甲类员工每月的人均绩效工资与公司月利润成正比,比例系数为a(a>0),乙类员工每月的绩效工资与公司月利润的平方成正比,比例系数为b(b>0).
(Ⅰ)若要求甲类员工的人数不超过乙类员工人数的2倍,问甲、乙两类员工各招聘多少人时,公司每月所付基础工资总额最少?
(Ⅱ)若该公司每月的利润为x(x>0)千元
( http: / / www.21cnjy.com ),记甲、乙两类员工该月人均工资分别为w甲千元和w乙千元,试比较w甲和w乙的大小.(月工资=月基础工资+月绩效工资)
22.在圆O:x2+y2=4上任取一点P,过点P作y轴额垂线段PQ,Q为垂足.当P在圆上运动时,线段PQ中点G的轨迹为C.
(Ⅰ)求C的方程;
(Ⅱ)直线l与圆O交于M,N两点,与曲线C交于E,F两点,若|MN|=,试判断∠EOF是否为定值?若是,求出该定值;若不是,说明理由.
2016-2017学年福建省厦门市高二(上)期末数学试卷(文科)
参考答案与试题解析
一、选择题(共12小题,每小题5分,满分60分)
1.已知{an}是等比数列,a1=2,a4=16,则数列{an}的公比q等于( )
A.2
B.﹣2
C.
D.﹣
【考点】等比数列的通项公式.
【分析】利用等比数列的通项公式即可得出.
【解答】解:由等比数列的性质可得:a4=,∴16=2q3,解得q=2.
故选:A.
2.设x∈R,则“x>1“是“x3>1”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
【考点】必要条件、充分条件与充要条件的判断.
【分析】利用充要条件的判断方法判断选项即可.
【解答】解:因为x∈R,“x>1“ “x3>1”,
所以“x>1“是“x3>1”的充要条件.
故选:C.
3.已知抛物线y2=12x上一点M到焦点的距离为8,则点M的横坐标为( )
A.2
B.3
C.4
D.5
【考点】抛物线的简单性质.
【分析】根据抛物线点到焦点的距离等于点到准线的距离,可得所求点的横坐标.
【解答】解:抛物线y2=12x的准线方程为x=﹣3,
∵抛物线y2=12x上点到焦点的距离等于8,
∴根据抛物线点到焦点的距离等于点到准线的距离,
∴可得所求点的横坐标为5.
故选D.
4.设实数x、y满足,则z=2x+y的最小值为( )
A.6
B.10
C.﹣6
D.﹣8
【考点】简单线性规划.
【分析】首先画出可行域,利用目标函数的几何意义求最小值.
【解答】解:由已知得到可行域如图:目标函数必须为y=﹣2x+z,当此直线经过图中C(﹣2,﹣2)时z最小,为﹣2×2=﹣6;
故选:C.
5.在△ABC中,角A,B,C所对的边分别为a,b,c,且bcosC+ccosB=acosC,则角C为( )
A.
B.
C.
D.
【考点】正弦定理.
【分析】已知等式利用正弦定理化简,利用两角和与差的正弦函数公式化简后,根据sinA不为0,求出cosC的值,即可确定出C的度数.
【解答】解:已知等式利用正弦定理化简得:sinBcosC+sinCcosB=sinAcosC,
即sin(B+C)=sinAcosC,
变形得:sinA=sinAcosC,
∵sinA≠0,
∴cosC=,
∴由C∈(0,π),可得∠C=.
故选:B.
6.已知{an}是等差数列,a1=﹣26,a8+a13=5,当{an}的前n项和Sn取最小值时,n等于( )
A.8
B.9
C.10
D.11
【考点】等差数列的前n项和.
【分析】利用等差数列的通项公式先求出公差,再求出等差数列前n项和公式,由此利用配方法能求出{an}的前n项和Sn取最小值时,n的值.
【解答】解:∵{an}是等差数列,a1=﹣26,a8+a13=5,
∴﹣26+7d﹣26+12d=5,
解得d=3,
∴Sn=﹣26n+==(n﹣)2+,
∴{an}的前n项和Sn取最小值时,n=9.
故选:B.
7.若双曲线=1(a>0,b>0)的一个焦点到一条渐近线的距离等于焦距的,则该双曲线的渐近线方程是( )
A.x±2y=0
B.2x±y=0
C.
x±y=0
D.xy=0
【考点】双曲线的简单性质.
【分析】由题设知b=×2c,因此b=c,a=c,所以=,由此可求出其渐近线方程.
【解答】解:对于双曲线=1(a>0,b>0)的一个焦点到一条渐近线的距离为=b,
所以b=×2c,
因此b=c,a=c,
所以=
因此其渐近线方程为x±y=0.
故选:D.
8.已知{an}是等比数列,{bn}是等差数列,若a2 a14=4a8,b8=a8,则数列{bn}的前15项和等于( )
A.30
B.40
C.60
D.120
【考点】等差数列的前n项和.
【分析】由等比数列通项公式求出b8=a8=4,由此利用等差数列前n项和公式能求出数列{bn}的前15项和.
【解答】解:∵{an}是等比数列,{bn}是等差数列,a2 a14=4a8,b8=a8,
∴=4a8,解得b8=a8=4,
∴数列{bn}的前15项和为:
S15=(b1+b15)=15b8=15×4=60.
故选:C.
9.若关于x的一元二次方程x2+ax﹣2=0有两个不相等的实根x1,x2,且x1<﹣1,x2>1,则实数a的取值范围是( )
A.a<﹣1
B.a>1
C.﹣1<a<1
D.a>2或a<﹣2
【考点】一元二次方程的根的分布与系数的关系.
【分析】由题意设f(x)=x2+ax﹣2,由条件、函数与方程的关系、一元二次函数的图象列出不等式,求出实数a的取值范围.
【解答】解:由题意设f(x)=x2+ax﹣2,
∵方程x2+ax﹣2=0有两个不相等的实根x1,x2,
且x1<﹣1,x2>1,
∴,则,
解得﹣1<a<1,
故选:C.
10.在△ABC中,角A,B,C所对的边分别为a,b,c,且a,2b,c成等比数列,则cosB的最小值为( )
A.
B.
C.
D.
【考点】等比数列的通项公式.
【分析】由a,2b,c成等比数列,知4b2=ac,由此利用余弦定理和基本不等式能求出cosB的最小值.
【解答】解:∵a,2b,c成等比数列,∴4b2=ac,
∴cosB==﹣≥1﹣=.
当且仅当a=c时,取等号,
∴cosB的最小值为.
故选:D.
11.已知函数f(x)=e2x﹣t,g(x)=tex﹣1,对任意x∈R,f(x)≥g(x)恒成立,则实数t的取值范围为( )
A.t≤1
B.t≤2﹣2
C.t≤2
D.t≤2﹣3
【考点】函数恒成立问题.
【分析】设F(x)=f(x)﹣g(x),则
( http: / / www.21cnjy.com )F(x)=f(x)﹣g(x)=e2x﹣tex+1﹣t对任意x∈R,最小值为0,由此能求出实数t的取值范围.
【解答】解:设F(x)=f(x)﹣g(x),
∵函数f(x)=e2x﹣t,g(x)=tex﹣1,对任意x∈R,f(x)≥g(x)恒成立,
∴F(x)=f(x)﹣g(x)=e2x﹣tex+1﹣t对任意x∈R,最小值为0,
F′(x)=2e2x﹣tex,由F′(x)=0,得x=ln,
∴F(ln)=﹣te+1﹣t≥0,
整理,得t2+4t﹣4≤0,
解得﹣2﹣2<t<2﹣2.
故选:B.
12.从一块短轴成为2m的椭圆形板材中截取一块面积最大的矩形,若椭圆的离心率为e,且e∈[,],则该矩形面积的取值范围是( )
A.[m2,2m2]
B.[2m2,3m2]
C.[3m2,4m2]
D.[4m2,5m2]
【考点】椭圆的简单性质.
【分析】在第一象限内取点(
( http: / / www.21cnjy.com )x,y),设x=acosθ,y=bsinθ,表示出圆的内接矩形长和宽,可得矩形的面积,由e∈[,],∴ 2b≤a≤,得:4b2≤2ab≤5b2即可
【解答】解:在第一象限内取点(x,y),设x=acosθ,y=bsinθ,(0<θ<)
则椭圆的内接矩形长为2acosθ,宽为2bsinθ,
内接矩形面积为2acosθ 2bsinθ=2absin2θ≤2ab,
椭圆的离心率为e,且e∈[,],∴ 2b≤a≤,
得:4b2≤2ab≤5b2,矩形面积的取值范围是[4m2,5m2].
故选:D.
二、填空题(本大题共有4小题,每小题5分,共20分)
13.命题p: x∈R,ex≥1,写出命题p的否定: x∈R,ex<1 .
【考点】命题的否定.
【分析】本题中的命题是一个全称命题,其否定是特称命题,依据全称命题的否定书写形式写出命题的否定即可
【解答】解:∵命题p: x∈R,ex≥1,
∴命题p的否定是“ x∈R,ex<1”
故答案为: x∈R,ex<1
14.已知方程+=1表示焦点在x轴上的椭圆,则实数m的取值范围为 ﹣<m<1 .
【考点】椭圆的简单性质.
【分析】根据题意,由椭圆的标准方程分析可得,解可得m的取值范围,即可得答案.
【解答】解:根据题意,方程+=1表示焦点在x轴上的椭圆,
则必有,
解可得:﹣<m<1,
即m的取值范围是﹣<m<1,
故答案为:﹣<m<1.
15.已知函数f(x)=,若an=f(n)(n∈N
),则数列{an}的前50项和等于 .
【考点】数列的求和.
【分析】n≤7时,an=f(n)=2n
( http: / / www.21cnjy.com )﹣10,可得a6=f(6),a7=f(7).x>7时,a8=f(8)=,a9=f(9)=,n≥10时,an=f(n)==f(n﹣4).即可得出.
【解答】解:n≤7时,an=f(n)=2n﹣10,
∴a6=f(6)=2×6﹣10=2,a7=f(7)=2×7﹣10=4.
n>7时,a8=f(8)==,a9=f(9)==,a10=f(10)==f(6)=2,a11=f(11)==f(7)=4,
a12=f(12)==f(8)=,…,n≥10时,an=f(n)==f(n﹣4).
∴数列{an}的前50项和为:
+11×=.
故答案为:.
16.一个三角形三边是连续的三个自然数,且最大角是最小角的2倍,则这个三角形的周长等于 15 .
【考点】余弦定理;正弦定理.
【分析】设三角形三边是连续的三个自
( http: / / www.21cnjy.com )然n﹣1,n,n+1,三个角分别为α,π﹣3α,2α,由正弦定理求得cosα=,再由余弦定理可得
(n﹣1)2=(n+1)2+n2﹣2(n+1)n ,求得n=5,从而得出结论.
【解答】解:设三边长分别为n﹣1,n,n+1,对应的角为A,B,C,
由题意知C=2A,
由正弦定理得=
即有cosA=,
又cosA==
所以=,
化简为n2﹣5n=0,解得n=5,
所以三边分别为4,5,6,其周长=4+5+6=15.
故答案为:15.
三、解答题(本大题共有6小题,共70分)
17.关于x的不等式x2﹣ax+b<0的解集为{x|2<x<3}.
(Ⅰ)求a+b;
(Ⅱ)若不等式﹣x2+bx+c>0的解集为空集,求c的取值范围.
【考点】一元二次不等式的解法.
【分析】(Ⅰ)根据一元二次不等式与对应方程的关系,利用根与系数的关系求出a、b的值,再求和;
(Ⅱ)把b=6代入不等式﹣x2+bx+c>0,由判别式△≤0求出c的取值范围.
【解答】解:(Ⅰ)由题意得:方程x2﹣ax+b=0的两根为2和3,…
所以,
解得,…
所以a+b=11;
…
(Ⅱ)由(Ⅰ)知b=6,
因为不等式﹣x2+bx+c>0的解集为空集,
所以△=62+4c≤0,…
解得c≤﹣9,
所以c的取值范围为(﹣∞,﹣9].
…
18.如图,在梯形ABCD中,AB∥CD,∠DAC=30°,∠CAB=45°,CD=﹣.
(Ⅰ)求AD的长;
(Ⅱ)若BC=,求△ABC的面积.
【考点】正弦定理.
【分析】(Ⅰ)由已知可求∠DCA=∠CAB=45°,进而利用正弦定理可求AD的值.
(Ⅱ)利用两角和的正弦函数公式可求sin∠ADC,利用正弦定理可求AC,由余弦定理可求AB,进而利用三角形面积公式即可计算得解.
【解答】(本题满分为12分)
解:(Ⅰ)因为AB∥CD,
所以∠DCA=∠CAB=45°,…
因为,…
所以AD==2﹣2.
…
(Ⅱ)∠ADC=180°﹣(30°+45°)=105°,
所以,sin∠ADC=sin(45°+60°)=sin45°cos60°+cos45°sin60°=,…
因为=,
所以AC=2,…
设AB=x,
因为,BC2=AC2+AB2﹣2AC ABcos∠CAB,
可得:x2﹣2x﹣6=0,
所以,AB=3,….
所以,S△ABC=AC ABsin∠CAB=3.
…
19.已知数列{an}满足a5=13,an+1﹣an=3(n∈N
),数列{bn}的前n项和Sn=1﹣(n∈N
).
(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)记Tn=a1b1+a2b2+a3b3+…+anbn,比较Tn与4的大小.
【考点】数列的求和;数列递推式.
【分析】(I)利用等差数列的通项公式可得an.利用数列递推关系可得bn.
(II)利用“错位相减法”与等比数列的求和公式即可得出.
【解答】解:(Ⅰ)∵an+1﹣an=3(n∈N
),∴数列{an}为等差数列,公差d=3,
又a5=a1+4d=13,得a1=1,∴an=1+3(n﹣1)=3n﹣2.
又因为数列{bn}的前n项和为Sn=1﹣(n∈N
).,
当n=1时,b1=S1=,
当n≥2时,bn=Sn﹣Sn﹣1=1﹣﹣=.,
∴bn=.
综上:an=3n﹣2,bn=.
(Ⅱ)anbn=(3n﹣2).
Tn=1×+7×+…+(3n﹣2)×,
=+…+(3n﹣5)×+(3n﹣2)×,
得:
=﹣(3n﹣2)×=﹣(3n﹣2)×,
∴Tn=1+3﹣(3n﹣2)×=4﹣<4.
20.已知直线l与抛物线y2=﹣x相交于A,B两点.A,B在准线上的摄影分别为A1,B1.
(Ⅰ)若线段AB的中点坐标为(﹣4,1),求直线l的方程;
(Ⅱ)若直线l方程为x=my﹣1,m∈R,求梯形AA1B1B的面积(用m表示).
【考点】抛物线的简单性质.
【分析】(Ⅰ)分类讨论,利用线段AB的中点坐标为(﹣4,1),设出直线方程,利用韦达定理,求出k,即可求直线l的方程;
(Ⅱ)若直线l方程为x=my﹣1,m∈R,求出上底、下底、高,即可求梯形AA1B1B的面积(用m表示).
【解答】解:(Ⅰ)当直线l斜率不存在时,直线l方程为:x=﹣4,此时AB中点坐标为(﹣4,0),不符合题意
….
当直线l斜率存在时,因为直线与抛物线交于两不同点,所以斜率不为0,
设直线l方程为:y﹣1=k(x+4),即y=kx+4k+1(k≠0),
代入抛物线方程得:k2x2+(8k2+2k+1)x+(4k+1)2=0…
设A(x1,y1),B(x2,y2),因为A,B中点坐标为(﹣4,1),所以x1+x2=﹣8,
所以=﹣8,得k=﹣…
直线l的方程为y﹣1=﹣(x+4),即x+2y+2=0…
(Ⅱ)联立x=my﹣1与抛物线方程得:y2+my﹣1=0.
所以y1+y2=﹣m,y1y2=﹣1
…..
又|AA1|=﹣x1+=﹣my1+,|BB1|=﹣x2+=﹣my2+,
所以|AA1|+|BB1|=﹣my1+﹣my2+=m2+
|A1B1|=|y1﹣y2|=,
∴梯形AA1B1B的面积S=…..
21.某公司要招聘甲、乙两类员工共
( http: / / www.21cnjy.com )150人,该公司员工的工资由基础工资组成.其中甲、乙两类员工每人每月的基础工资分别为2千元和3千元,甲类员工每月的人均绩效工资与公司月利润成正比,比例系数为a(a>0),乙类员工每月的绩效工资与公司月利润的平方成正比,比例系数为b(b>0).
(Ⅰ)若要求甲类员工的人数不超过乙类员工人数的2倍,问甲、乙两类员工各招聘多少人时,公司每月所付基础工资总额最少?
(Ⅱ)若该公司每月的利润为x(x>0)千元,
( http: / / www.21cnjy.com )记甲、乙两类员工该月人均工资分别为w甲千元和w乙千元,试比较w甲和w乙的大小.(月工资=月基础工资+月绩效工资)
【考点】函数模型的选择与应用.
【分析】(Ⅰ)设招聘甲类员工人数为x,乙类员工人数为,求出公司每月所付的基础工资总额,即可得出结论;
(Ⅱ)由已知,w甲=2+a
( http: / / www.21cnjy.com )x,w乙=3+bx2,w乙﹣w甲=(3+bx2)﹣(2+ax)=bx2﹣ax+1(a>0,b>0,x>0),分类讨论,可得结论.
【解答】解:(Ⅰ)设招聘甲类员工人数为x,乙类员工人数为,公司每月所付的基础工资总额为y千元,
因为x≤2,所以0<x≤100,x∈N…
因为y=2x+3=450﹣x…
x=100时,ymin=350,
所以甲类员工招聘100人,乙类员工招聘50人
时,公司每月所付的基础工资
总额最少为
350000元…
(Ⅱ)由已知,w甲=2+ax,w乙=3+bx2…
w乙﹣w甲=(3+bx2)﹣(2+ax)=bx2﹣ax+1(a>0,b>0,x>0)…
△=a2﹣4b
(
i)当△<0,即a2<4b时,bx2﹣ax+1=0无实数根,
此时w乙﹣w甲>0,即w乙>w甲;…
(
ii)当△=0,即a2=4b时,bx2﹣ax+1=0有两个相等正实根,
①当x=时,w乙=w甲;…
②当x>0且x≠时,w乙>w甲;…
(
iii)当△>0,即a2>4b时,bx2﹣ax+1=0有两个不相等正数根和,
①当x∈(0,)∪(,+∞)时,w乙>w甲;…
②当x∈(,)时,w乙<w甲;…
③当x=或时,w乙=w甲…
22.在圆O:x2+y2=4上任取一点P,过点P作y轴额垂线段PQ,Q为垂足.当P在圆上运动时,线段PQ中点G的轨迹为C.
(Ⅰ)求C的方程;
(Ⅱ)直线l与圆O交于M,N两点,与曲线C交于E,F两点,若|MN|=,试判断∠EOF是否为定值?若是,求出该定值;若不是,说明理由.
【考点】直线与椭圆的位置关系;轨迹方程.
【分析】(Ⅰ)设G(x,
( http: / / www.21cnjy.com )y),P(x0,y0),所以Q(0,y0),由中点坐标公式得x0=2x,y0=y,由P(x0,y0)在圆O上,能求出C的方程.
(Ⅱ)求出点O到直线l的距离d=,当直线l斜率不存在时,∠EOF=90°;当直线l斜率存在时,设直线l:y=kx+m,求出5m2=4(k2+1),由得:(4+k2)x2+2mkx+m2﹣4=0,由此利用根的判别式、韦达定理,向量数量积求出∠EOF=90°.由此得到∠EOF=90°为定值.
【解答】解:(Ⅰ)设G(x,y),P(x0,y0),所以Q(0,y0),…
因为点G是线段PQ中点,所以x0=2x,y0=y,…..…..…
又P(x0,y0)在圆O上,所以(2x)2+y2=4,
即C的方程为:.…
(Ⅱ)设点O到直线l的距离为d,则d===,…
当直线l斜率不存在时,直线l方程:x=±,代入椭圆方程得:y=,
不妨设E(),F(,﹣),此时∠EOF=90°,…
当直线l斜率存在时,设直线l:y=kx+m,得kx﹣y+m=0,
所以d==,所以5m2=4(k2+1),…
由得:(4+k2)x2+2mkx+m2﹣4=0,…
(k2+16)>0,
设E(x1,y1),F(x2,y2),所以,,
=x1x2+y1y2=x1x2+(kx1+m)(kx2+m)=(1+k2)x1x2+mk(x1+x2)+m2
=(1+k2)+mk+m2=,…
把5m2=4(k2+1)代入上式得:
=0,所以OE⊥OF,即∠EOF=90°.
综上所述∠EOF=90°为定值.…
2017年3月14日
