9.1.1 认识三角形——三角形中的主要线段 同步练习
文档属性
| 名称 | 9.1.1 认识三角形——三角形中的主要线段 同步练习 |

|
|
| 格式 | zip | ||
| 文件大小 | 473.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-16 00:00:00 | ||
图片预览


文档简介
9.1.1 认识三角形——三角形中的主要线段
核心笔记: 1.三角形的高:从三角形的一个顶点向对边或其延长线作垂线,顶点与垂足间的线段.
2.三角形的中线:连结三角形的一个顶点与对边中点的线段.
3.三角形的角平分线:三角形的一个内角的平分线与对边相交于一点,顶点与交点之间的线段.
基础训练
1.如图,∠1=∠2,∠3=∠4,下列选项中错误的是( )
A.BD是△ABC的角平分线
B.CE是△BCD的角平分线
C.∠3=∠ACB
D.CE是△ABC的角平分线
2.三角形一边上的中线把原三角形一定分成两个( )
A.形状相同的三角形 B.面积相等的三角形
C.直角三角形 D.周长相等的三角形
3.已知BD是△ABC的中线,AB=5,BC=3,△ABD和△BCD的周长的差是( )
A.2 B.3 C.6 D.不能确定
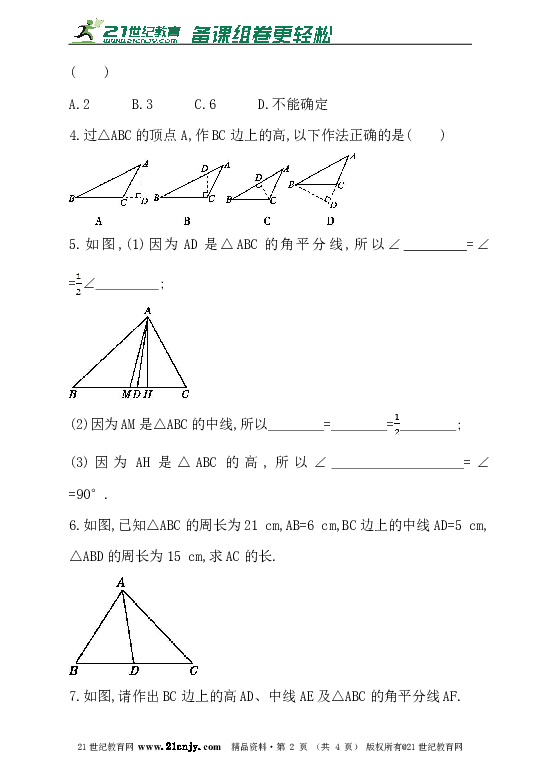
4.过△ABC的顶点A,作BC边上的高,以下作法正确的是( )
5.如图,(1)因为AD是△ABC的角平分线,所以∠_________=∠ =∠ ;?21世纪教育网版权所有
(2)因为AM是△ABC的中线,所以 = = ;?
(3)因为AH是△ABC的高,所以∠ =∠ =90°.?
6.如图,已知△ABC的周长为21 cm,AB=6 cm,BC边上的中线AD=5 cm,△ABD的周长为15 cm,求AC的长.21教育网
7.如图,请作出BC边上的高AD、中线AE及△ABC的角平分线AF.
8.如图,在△ABC中,AD是BC边上的中线,若△ABD和△ADC的周长之差为4(AB>AC),AB与AC的长度之和为14,求AB和AC的长.
培优提升
1.下列结论:
①三角形的角平分线、中线、高都是线段;
②直角三角形只有一条高;
③三角形的中线可能在三角形外部;
④三角形的高都在三角形内部.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
2.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不能确定
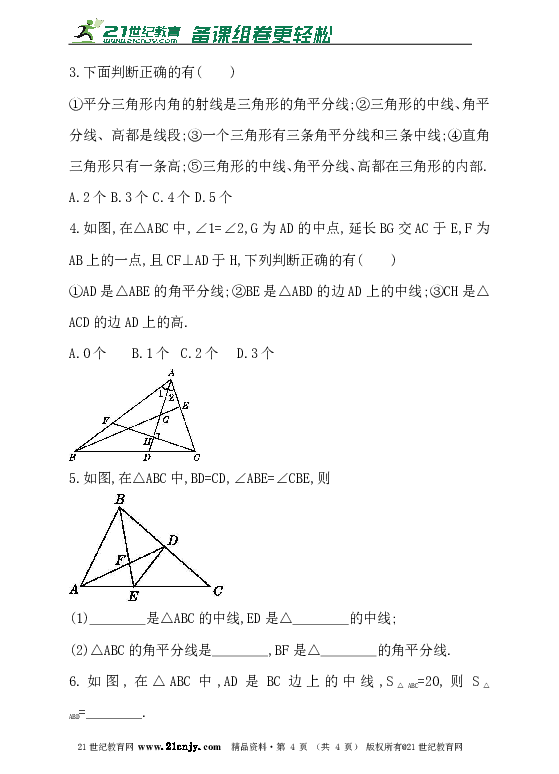
3.下面判断正确的有( )
①平分三角形内角的射线是三角形的角平分线;②三角形的中线、角平分线、高都是线段;③一个三角形有三条角平分线和三条中线;④直角三角形只有一条高;⑤三角形的中线、角平分线、高都在三角形的内部.
A.2个 B.3个 C.4个 D.5个
4.如图,在△ABC中,∠1=∠2,G为AD的中点,延长BG交AC于E,F为AB上的一点,且CF⊥AD于H,下列判断正确的有( )
①AD是△ABE的角平分线;②BE是△ABD的边AD上的中线;③CH是△ACD的边AD上的高.
A.0个 B.1个 C.2个 D.3个
5.如图,在△ABC中,BD=CD,∠ABE=∠CBE,则
(1) 是△ABC的中线,ED是△ 的中线;?
(2)△ABC的角平分线是 ,BF是△ 的角平分线.?
6.如图,在△ABC中,AD是BC边上的中线,S△ABC=20,则S△ABD= .?
7.如图,已知AE是∠BAC的平分线,∠1=∠D.
求证:∠1=∠2.
8.幼儿园老师给6个小朋友过生日,定做了一个三角形蛋糕,示意图如图所示,只需切三刀就能平均分给6个小朋友,你能做到吗?画一画.
9.如图,在△ABC中,CE⊥AB,AD⊥BC,且AB=3,BC=6,则CE与AD的比是多少?
10.如图,已知在正方形网格中,每个小方格都是边长为1的正方形,A,B两点在网格格点上,若点C也在网格格点上,以A,B,C为顶点的三角形的面积为1,则满足条件的点C的个数是( )
A.2 B.3 C.4 D.5
参考答案
【基础训练】
1.【答案】D 2.【答案】B 3.【答案】A 4.【答案】A
5.【答案】(1)BAD;CAD;BAC (2)BM;CM;BC
(3)AHB;AHC
解:(1)∵AD是△ABC的角平分线,∴∠BAD=∠CAD=∠BAC;(2)∵AM是△ABC的中线,∴BM=CM=BC;(3)∵AH是△ABC的高,∴AH⊥BC,∴∠AHB=∠AHC=90°.21cnjy.com
6.解:∵AB=6 cm,AD=5 cm,△ABD的周长为15 cm,∴BD=15-6-5=4 (cm),∵AD是BC边上的中线,∴BC=2BD=2×4=8 (cm),∵△ABC的周长为21 cm,∴AC=21-6-8=7 (cm).www.21-cn-jy.com
7.解:如图所示.
8.解:∵AD是BC边上的中线,∴BD=CD,
∴△ABD的周长-△ADC的周长=(AB+AD+BD)-(AC+AD+CD)=AB-AC=4,
即AB-AC=4①,又AB+AC=14②,
①+②,得2AB=18,
解得AB=9,
②-①,得2AC=10,
解得AC=5,
∴AB和AC的长分别为9,5.
【培优提升】
1.【答案】A 2.【答案】B 3.【答案】A
4.【答案】B
解:由∠1=∠2知AD平分∠BAE,但AD不是△ABE内的线段,因此①不正确;同样BE虽然经过△ABD的边AD的中点G,但BE也不是△ABD内的线段,因此②也不正确;CH⊥AD于H,由三角形的高的概念知CH是△ACD的边AD上的高,因此③正确,故选B.2·1·c·n·j·y
5.【答案】(1)AD;BEC (2)BE;ABD
解:(1)∵BD=CD,∴AD是△ABC的中线,ED是△BEC的中线;(2)∵∠ABE=∠CBE,∴△ABC的角平分线是BE,BF是△ABD的角平分线.
6.【答案】10
解:∵AD是BC边上的中线,∴BD=CD,易知S△ABD=S△ADC,∴S△ABC=2S△ABD.又∵S△ABC=20,∴2S△ABD=20,∴S△ABD=10.21·cn·jy·com
7.证明:∵∠1=∠D,
∴AE∥DC(同位角相等,两直线平行),
∴∠EAC=∠2(两直线平行,内错角相等),
∵AE是∠BAC的平分线,
∴∠1=∠EAC,∴∠1=∠2.
8.解:能做到.沿三角形的三条中线切开即可,如图所示.
9.解:根据△ABC的面积=AB·CE=BC·AD,得===2,
所以CE:AD=2:1.
10.【答案】C
解:点C所有的情况如图所示.
核心笔记: 1.三角形的高:从三角形的一个顶点向对边或其延长线作垂线,顶点与垂足间的线段.
2.三角形的中线:连结三角形的一个顶点与对边中点的线段.
3.三角形的角平分线:三角形的一个内角的平分线与对边相交于一点,顶点与交点之间的线段.
基础训练
1.如图,∠1=∠2,∠3=∠4,下列选项中错误的是( )
A.BD是△ABC的角平分线
B.CE是△BCD的角平分线
C.∠3=∠ACB
D.CE是△ABC的角平分线
2.三角形一边上的中线把原三角形一定分成两个( )
A.形状相同的三角形 B.面积相等的三角形
C.直角三角形 D.周长相等的三角形
3.已知BD是△ABC的中线,AB=5,BC=3,△ABD和△BCD的周长的差是( )
A.2 B.3 C.6 D.不能确定
4.过△ABC的顶点A,作BC边上的高,以下作法正确的是( )
5.如图,(1)因为AD是△ABC的角平分线,所以∠_________=∠ =∠ ;?21世纪教育网版权所有
(2)因为AM是△ABC的中线,所以 = = ;?
(3)因为AH是△ABC的高,所以∠ =∠ =90°.?
6.如图,已知△ABC的周长为21 cm,AB=6 cm,BC边上的中线AD=5 cm,△ABD的周长为15 cm,求AC的长.21教育网
7.如图,请作出BC边上的高AD、中线AE及△ABC的角平分线AF.
8.如图,在△ABC中,AD是BC边上的中线,若△ABD和△ADC的周长之差为4(AB>AC),AB与AC的长度之和为14,求AB和AC的长.
培优提升
1.下列结论:
①三角形的角平分线、中线、高都是线段;
②直角三角形只有一条高;
③三角形的中线可能在三角形外部;
④三角形的高都在三角形内部.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
2.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不能确定
3.下面判断正确的有( )
①平分三角形内角的射线是三角形的角平分线;②三角形的中线、角平分线、高都是线段;③一个三角形有三条角平分线和三条中线;④直角三角形只有一条高;⑤三角形的中线、角平分线、高都在三角形的内部.
A.2个 B.3个 C.4个 D.5个
4.如图,在△ABC中,∠1=∠2,G为AD的中点,延长BG交AC于E,F为AB上的一点,且CF⊥AD于H,下列判断正确的有( )
①AD是△ABE的角平分线;②BE是△ABD的边AD上的中线;③CH是△ACD的边AD上的高.
A.0个 B.1个 C.2个 D.3个
5.如图,在△ABC中,BD=CD,∠ABE=∠CBE,则
(1) 是△ABC的中线,ED是△ 的中线;?
(2)△ABC的角平分线是 ,BF是△ 的角平分线.?
6.如图,在△ABC中,AD是BC边上的中线,S△ABC=20,则S△ABD= .?
7.如图,已知AE是∠BAC的平分线,∠1=∠D.
求证:∠1=∠2.
8.幼儿园老师给6个小朋友过生日,定做了一个三角形蛋糕,示意图如图所示,只需切三刀就能平均分给6个小朋友,你能做到吗?画一画.
9.如图,在△ABC中,CE⊥AB,AD⊥BC,且AB=3,BC=6,则CE与AD的比是多少?
10.如图,已知在正方形网格中,每个小方格都是边长为1的正方形,A,B两点在网格格点上,若点C也在网格格点上,以A,B,C为顶点的三角形的面积为1,则满足条件的点C的个数是( )
A.2 B.3 C.4 D.5
参考答案
【基础训练】
1.【答案】D 2.【答案】B 3.【答案】A 4.【答案】A
5.【答案】(1)BAD;CAD;BAC (2)BM;CM;BC
(3)AHB;AHC
解:(1)∵AD是△ABC的角平分线,∴∠BAD=∠CAD=∠BAC;(2)∵AM是△ABC的中线,∴BM=CM=BC;(3)∵AH是△ABC的高,∴AH⊥BC,∴∠AHB=∠AHC=90°.21cnjy.com
6.解:∵AB=6 cm,AD=5 cm,△ABD的周长为15 cm,∴BD=15-6-5=4 (cm),∵AD是BC边上的中线,∴BC=2BD=2×4=8 (cm),∵△ABC的周长为21 cm,∴AC=21-6-8=7 (cm).www.21-cn-jy.com
7.解:如图所示.
8.解:∵AD是BC边上的中线,∴BD=CD,
∴△ABD的周长-△ADC的周长=(AB+AD+BD)-(AC+AD+CD)=AB-AC=4,
即AB-AC=4①,又AB+AC=14②,
①+②,得2AB=18,
解得AB=9,
②-①,得2AC=10,
解得AC=5,
∴AB和AC的长分别为9,5.
【培优提升】
1.【答案】A 2.【答案】B 3.【答案】A
4.【答案】B
解:由∠1=∠2知AD平分∠BAE,但AD不是△ABE内的线段,因此①不正确;同样BE虽然经过△ABD的边AD的中点G,但BE也不是△ABD内的线段,因此②也不正确;CH⊥AD于H,由三角形的高的概念知CH是△ACD的边AD上的高,因此③正确,故选B.2·1·c·n·j·y
5.【答案】(1)AD;BEC (2)BE;ABD
解:(1)∵BD=CD,∴AD是△ABC的中线,ED是△BEC的中线;(2)∵∠ABE=∠CBE,∴△ABC的角平分线是BE,BF是△ABD的角平分线.
6.【答案】10
解:∵AD是BC边上的中线,∴BD=CD,易知S△ABD=S△ADC,∴S△ABC=2S△ABD.又∵S△ABC=20,∴2S△ABD=20,∴S△ABD=10.21·cn·jy·com
7.证明:∵∠1=∠D,
∴AE∥DC(同位角相等,两直线平行),
∴∠EAC=∠2(两直线平行,内错角相等),
∵AE是∠BAC的平分线,
∴∠1=∠EAC,∴∠1=∠2.
8.解:能做到.沿三角形的三条中线切开即可,如图所示.
9.解:根据△ABC的面积=AB·CE=BC·AD,得===2,
所以CE:AD=2:1.
10.【答案】C
解:点C所有的情况如图所示.
