9.1.3 三角形的内角和与外角和——三角形外角和 同步练习
文档属性
| 名称 | 9.1.3 三角形的内角和与外角和——三角形外角和 同步练习 |

|
|
| 格式 | zip | ||
| 文件大小 | 440.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-16 22:24:40 | ||
图片预览

文档简介
9.1.3 三角形的内角和与外角和——三角形外角和
核心笔记: 1.三角形外角的性质:
(1)三角形的一个外角等于与它不相邻的两个内角的和.
(2)三角形的一个外角大于任何一个与它不相邻的内角.
2.三角形的外角和等于360°.
基础训练
1.如图,在△ABC中,CD是∠ACB的平分线,∠A=80°,∠ACB=60°,那么∠BDC=( )【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com )
A.80° B.90°
C.100° D.110°
2.如图,CF是△ABC的外角∠ACM的平分线,且CF∥AB,∠ACF=50°,则∠B的度数为( )21·世纪*教育网
( http: / / www.21cnjy.com )
A.80° B.40°
C.60° D.50°
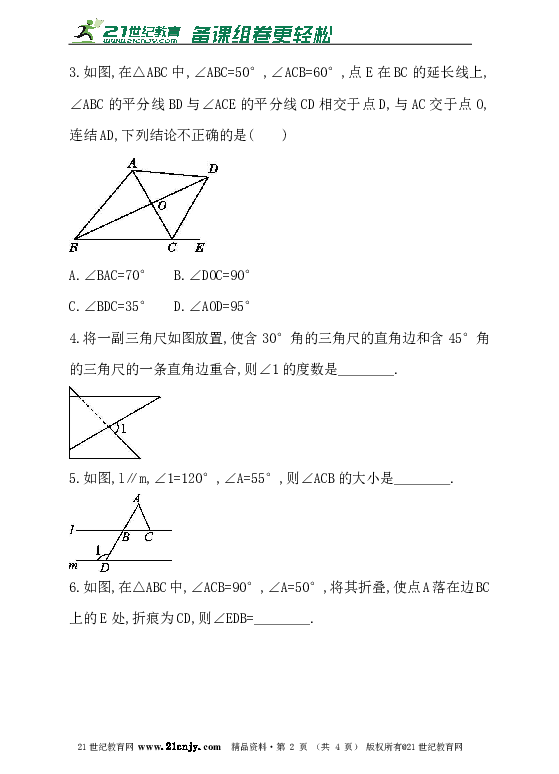
3.如图,在△ABC中,∠ABC=50° ( http: / / www.21cnjy.com ),∠ACB=60°,点E在BC的延长线上,∠ABC的平分线BD与∠ACE的平分线CD相交于点D,与AC交于点O,连结AD,下列结论不正确的是( )2·1·c·n·j·y
( http: / / www.21cnjy.com )
A.∠BAC=70° B.∠DOC=90°
C.∠BDC=35° D.∠AOD=95°
4.将一副三角尺如图放置,使含30°角的三角尺的直角边和含45°角的三角尺的一条直角边重合,则∠1的度数是 .
( http: / / www.21cnjy.com )
5.如图,l∥m,∠1=120°,∠A=55°,则∠ACB的大小是 .
( http: / / www.21cnjy.com )
6.如图,在△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边BC上的E处,折痕为CD,则∠EDB= .21cnjy.com
( http: / / www.21cnjy.com )
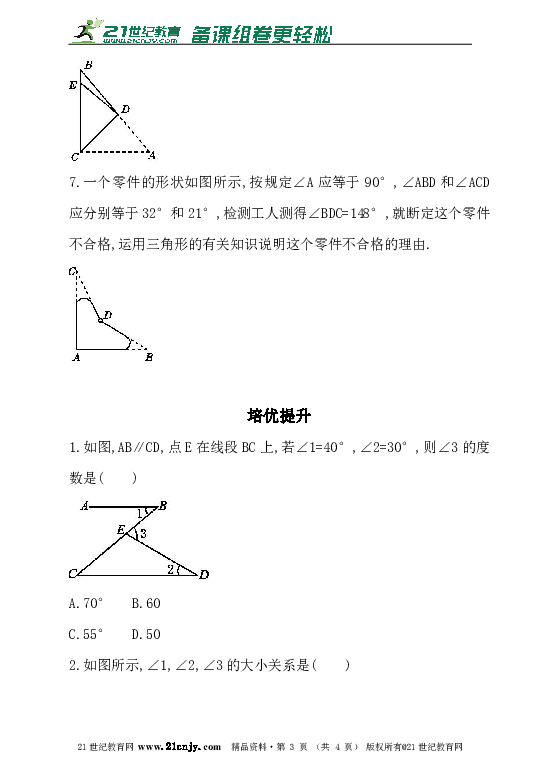
7.一个零件的形状如图所示,按规定∠A应等 ( http: / / www.21cnjy.com )于90°,∠ABD和∠ACD应分别等于32°和21°,检测工人测得∠BDC=148°,就断定这个零件不合格,运用三角形的有关知识说明这个零件不合格的理由.
( http: / / www.21cnjy.com )
培优提升
1.如图,AB∥CD,点E在线段BC上,若∠1=40°,∠2=30°,则∠3的度数是( )
( http: / / www.21cnjy.com )
A.70° B.60
C.55° D.50
2.如图所示,∠1,∠2,∠3的大小关系是( )
( http: / / www.21cnjy.com )
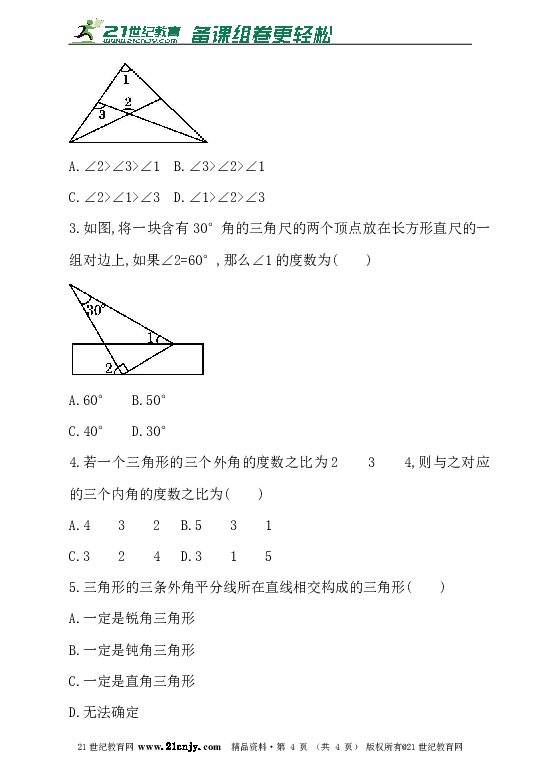
A.∠2>∠3>∠1 B.∠3>∠2>∠1
C.∠2>∠1>∠3 D.∠1>∠2>∠3
3.如图,将一块含有30°角的三角尺的两个顶点放在长方形直尺的一组对边上,如果∠2=60°,那么∠1的度数为( )www-2-1-cnjy-com
( http: / / www.21cnjy.com )
A.60° B.50°
C.40° D.30°
4.若一个三角形的三个外角的度数之比为2 3 4,则与之对应的三个内角的度数之比为( )
A.4 3 2 B.5 3 1
C.3 2 4 D.3 1 5
5.三角形的三条外角平分线所在直线相交构成的三角形( )
A.一定是锐角三角形
B.一定是钝角三角形
C.一定是直角三角形
D.无法确定
6.如图,已知DO平分∠ADC,BO平分∠ABC,且∠A=27°,∠O=33°,则∠C= .
( http: / / www.21cnjy.com )
7.如图,∠1+∠2+∠3+∠4= 度.
( http: / / www.21cnjy.com )
8.将一副三角尺拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F.
( http: / / www.21cnjy.com )
(1)试说明:CF∥AB;
(2)求∠DFC的度数.
9.如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个动点,PE⊥AD交BC的延长线于点E. 21·cn·jy·com
(1)若∠B=35°,∠ACB=85°,求∠E的度数;
(2)当P点在线段AD上运动时,猜想∠E与∠B,∠ACB的数量关系,写出结论不需要说明.
( http: / / www.21cnjy.com )
10.如图,在△ABC中,AB>AC,E,F分别是AB,AC上一点,∠AEF=∠AFE,EF的延长线与BC的延长线交于点G. 21世纪教育网版权所有
试说明:∠G=(∠ACB-∠B).
( http: / / www.21cnjy.com )
参考答案
【基础训练】
1.【答案】D 2.【答案】D 3.【答案】B
4.【答案】75° 5.【答案】65° 6.【答案】10°
7.解:理由如下:
如图,连结AD并延长,则∠1=∠ACD+∠CAD,
( http: / / www.21cnjy.com )
∠2=∠ABD+∠BAD,
所以∠BDC=∠ACD+∠ABD+∠CAB=21°+32°+90°=143°,
因为检测工人测得∠BDC=148°,
所以这个零件不合格.
【培优提升】
1.【答案】A 2.【答案】A 3.【答案】D
4.【答案】B 5.【答案】A
6.【答案】39°
解:由已知,得∠ABG=∠OBH,∠ODG=∠CDH.
比较△ABG和△OGD的角的关系,得∠A+∠ABG=∠O+∠ODG①,
同理比较△CDH和△OBH的角的关系,得∠C+∠CDH=∠O+∠OBH②,
①+②,得∠A+∠C=2∠O.
∴∠C=2×33°-27°=39°.
7.【答案】540
解:设∠1+∠2=x°,∠3+∠4=y°.易知360-x+360-y=180,所以∠1+∠2+∠3+∠4=540°.21教育网
8.解:(1)∵CF平分∠DCE,∴∠1=∠2=∠DCE.∵∠DCE=90°,∴∠1=45°.∵∠3=45°,∴∠1=∠3,∴AB∥CF.www.21-cn-jy.com
(2)∵∠D=30°,∠1=45°,
∴∠DFC=180°-30°-45°=105°.
9.解:(1)∵∠B=35°,∠ACB=85°,
∴∠BAC=180°-35°-85°=60°.
∵AD平分∠BAC,
∴∠DAC=×60°=30°,
∴∠ADC=180°-85°-30°=65°,
∵PE⊥AD,
∴∠DPE=90°,
∴∠E=180°-90°-65°=25°.
(2)∠E=(∠ACB-∠B).
10.解:∵∠AEF=∠AFE,∠AFE=∠GFC,
∴∠AEF=∠GFC.
∵∠AEF=∠B+∠G,
∴∠GFC=∠B+∠G,
又∵∠ACB=∠GFC+∠G,
∴∠ACB=∠B+2∠G.
∴∠G=(∠ACB-∠B).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 8 页 (共 8 页) 版权所有@21世纪教育网
核心笔记: 1.三角形外角的性质:
(1)三角形的一个外角等于与它不相邻的两个内角的和.
(2)三角形的一个外角大于任何一个与它不相邻的内角.
2.三角形的外角和等于360°.
基础训练
1.如图,在△ABC中,CD是∠ACB的平分线,∠A=80°,∠ACB=60°,那么∠BDC=( )【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com )
A.80° B.90°
C.100° D.110°
2.如图,CF是△ABC的外角∠ACM的平分线,且CF∥AB,∠ACF=50°,则∠B的度数为( )21·世纪*教育网
( http: / / www.21cnjy.com )
A.80° B.40°
C.60° D.50°
3.如图,在△ABC中,∠ABC=50° ( http: / / www.21cnjy.com ),∠ACB=60°,点E在BC的延长线上,∠ABC的平分线BD与∠ACE的平分线CD相交于点D,与AC交于点O,连结AD,下列结论不正确的是( )2·1·c·n·j·y
( http: / / www.21cnjy.com )
A.∠BAC=70° B.∠DOC=90°
C.∠BDC=35° D.∠AOD=95°
4.将一副三角尺如图放置,使含30°角的三角尺的直角边和含45°角的三角尺的一条直角边重合,则∠1的度数是 .
( http: / / www.21cnjy.com )
5.如图,l∥m,∠1=120°,∠A=55°,则∠ACB的大小是 .
( http: / / www.21cnjy.com )
6.如图,在△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边BC上的E处,折痕为CD,则∠EDB= .21cnjy.com
( http: / / www.21cnjy.com )
7.一个零件的形状如图所示,按规定∠A应等 ( http: / / www.21cnjy.com )于90°,∠ABD和∠ACD应分别等于32°和21°,检测工人测得∠BDC=148°,就断定这个零件不合格,运用三角形的有关知识说明这个零件不合格的理由.
( http: / / www.21cnjy.com )
培优提升
1.如图,AB∥CD,点E在线段BC上,若∠1=40°,∠2=30°,则∠3的度数是( )
( http: / / www.21cnjy.com )
A.70° B.60
C.55° D.50
2.如图所示,∠1,∠2,∠3的大小关系是( )
( http: / / www.21cnjy.com )
A.∠2>∠3>∠1 B.∠3>∠2>∠1
C.∠2>∠1>∠3 D.∠1>∠2>∠3
3.如图,将一块含有30°角的三角尺的两个顶点放在长方形直尺的一组对边上,如果∠2=60°,那么∠1的度数为( )www-2-1-cnjy-com
( http: / / www.21cnjy.com )
A.60° B.50°
C.40° D.30°
4.若一个三角形的三个外角的度数之比为2 3 4,则与之对应的三个内角的度数之比为( )
A.4 3 2 B.5 3 1
C.3 2 4 D.3 1 5
5.三角形的三条外角平分线所在直线相交构成的三角形( )
A.一定是锐角三角形
B.一定是钝角三角形
C.一定是直角三角形
D.无法确定
6.如图,已知DO平分∠ADC,BO平分∠ABC,且∠A=27°,∠O=33°,则∠C= .
( http: / / www.21cnjy.com )
7.如图,∠1+∠2+∠3+∠4= 度.
( http: / / www.21cnjy.com )
8.将一副三角尺拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F.
( http: / / www.21cnjy.com )
(1)试说明:CF∥AB;
(2)求∠DFC的度数.
9.如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个动点,PE⊥AD交BC的延长线于点E. 21·cn·jy·com
(1)若∠B=35°,∠ACB=85°,求∠E的度数;
(2)当P点在线段AD上运动时,猜想∠E与∠B,∠ACB的数量关系,写出结论不需要说明.
( http: / / www.21cnjy.com )
10.如图,在△ABC中,AB>AC,E,F分别是AB,AC上一点,∠AEF=∠AFE,EF的延长线与BC的延长线交于点G. 21世纪教育网版权所有
试说明:∠G=(∠ACB-∠B).
( http: / / www.21cnjy.com )
参考答案
【基础训练】
1.【答案】D 2.【答案】D 3.【答案】B
4.【答案】75° 5.【答案】65° 6.【答案】10°
7.解:理由如下:
如图,连结AD并延长,则∠1=∠ACD+∠CAD,
( http: / / www.21cnjy.com )
∠2=∠ABD+∠BAD,
所以∠BDC=∠ACD+∠ABD+∠CAB=21°+32°+90°=143°,
因为检测工人测得∠BDC=148°,
所以这个零件不合格.
【培优提升】
1.【答案】A 2.【答案】A 3.【答案】D
4.【答案】B 5.【答案】A
6.【答案】39°
解:由已知,得∠ABG=∠OBH,∠ODG=∠CDH.
比较△ABG和△OGD的角的关系,得∠A+∠ABG=∠O+∠ODG①,
同理比较△CDH和△OBH的角的关系,得∠C+∠CDH=∠O+∠OBH②,
①+②,得∠A+∠C=2∠O.
∴∠C=2×33°-27°=39°.
7.【答案】540
解:设∠1+∠2=x°,∠3+∠4=y°.易知360-x+360-y=180,所以∠1+∠2+∠3+∠4=540°.21教育网
8.解:(1)∵CF平分∠DCE,∴∠1=∠2=∠DCE.∵∠DCE=90°,∴∠1=45°.∵∠3=45°,∴∠1=∠3,∴AB∥CF.www.21-cn-jy.com
(2)∵∠D=30°,∠1=45°,
∴∠DFC=180°-30°-45°=105°.
9.解:(1)∵∠B=35°,∠ACB=85°,
∴∠BAC=180°-35°-85°=60°.
∵AD平分∠BAC,
∴∠DAC=×60°=30°,
∴∠ADC=180°-85°-30°=65°,
∵PE⊥AD,
∴∠DPE=90°,
∴∠E=180°-90°-65°=25°.
(2)∠E=(∠ACB-∠B).
10.解:∵∠AEF=∠AFE,∠AFE=∠GFC,
∴∠AEF=∠GFC.
∵∠AEF=∠B+∠G,
∴∠GFC=∠B+∠G,
又∵∠ACB=∠GFC+∠G,
∴∠ACB=∠B+2∠G.
∴∠G=(∠ACB-∠B).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 8 页 (共 8 页) 版权所有@21世纪教育网
