9.1.4 三角形的三边关系 同步练习
文档属性
| 名称 | 9.1.4 三角形的三边关系 同步练习 |

|
|
| 格式 | zip | ||
| 文件大小 | 448.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-16 22:27:46 | ||
图片预览

文档简介
9.1.4 三角形的三边关系
核心笔记: 1.三角形的三边关系:三角形的任何两边之和大于第三边,三角形的任何两边之差小于第三边.若已知三角形的两边长为m,n(m≥n),则第三边长x的取值范围是m-n2.三角形的稳定性:如果三角形的三条边固定,那么三角形的形状和大小就完全确定了.三角形的这个性质叫做三角形的稳定性.
基础训练
1.一个三角形的三条边长分别为1,2,x,则x的取值范围是( )
A.1≤x≤3 B.1C.1≤x<3 D.12.以下列各组线段为边,能组成三角形的是( )
A.1 cm,2 cm,4 cm B.4 cm,6 cm,8 cm
C.5 cm,6 cm,12 cm D.2 cm,3 cm,5 cm
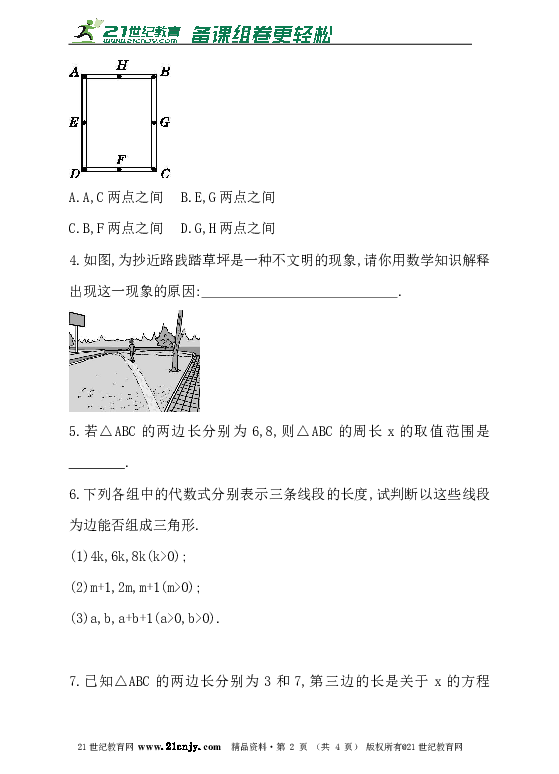
3.如图,工人师傅做了一个长方形窗框ABCD,E,F,G,H分别是四条边上的中点,为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在( )21世纪教育网版权所有
A.A,C两点之间 B.E,G两点之间
C.B,F两点之间 D.G,H两点之间
4.如图,为抄近路践踏草坪是一种不文明的现象,请你用数学知识解释出现这一现象的原因: .
5.若△ABC的两边长分别为6,8,则△ABC的周长x的取值范围是________.
6.下列各组中的代数式分别表示三条线段的长度,试判断以这些线段为边能否组成三角形.
(1)4k,6k,8k(k>0);
(2)m+1,2m,m+1(m>0);
(3)a,b,a+b+1(a>0,b>0).
7.已知△ABC的两边长分别为3和7,第三边的长是关于x的方程=x+1的解,求a的取值范围.
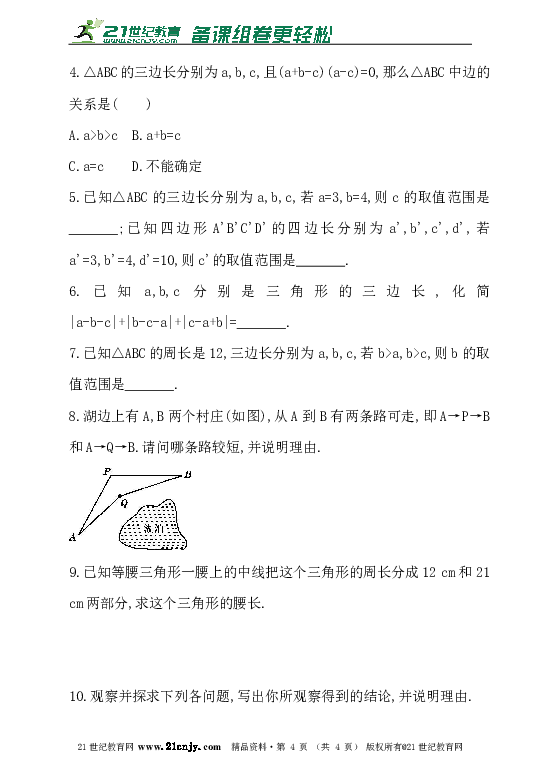
8.如图所示,已知P是△ABC内一点.
试说明PA+PB+PC>(AB+BC+AC).
培优提升
1.在等腰三角形ABC中,AB=AC,其周长为20 cm,则AB边的取值范围是( )
A.1 cmC.4 cm2.有长为3 cm,6 cm,8 cm,9 cm的四条线段,任选其中的三条线段组成一个三角形,则最多能组成三角形的个数为( )www.21-cn-jy.com
A.1 B.2 C.3 D.4
3.一个等腰三角形的两边长分别是3和7,则它的周长为( )
A.17 B.15 C.13 D.13或17
4.△ABC的三边长分别为a,b,c,且(a+b-c)(a-c)=0,那么△ABC中边的关系是( )2·1·c·n·j·y
A.a>b>c B.a+b=c
C.a=c D.不能确定
5.已知△ABC的三边长分别为a,b,c,若a=3,b=4,则c的取值范围是_______;已知四边形A'B'C'D'的四边长分别为a',b',c',d',若a'=3,b'=4,d'=10,则c'的取值范围是_______.【来源:21·世纪·教育·网】
6.已知a,b,c分别是三角形的三边长,化简|a-b-c|+|b-c-a|+|c-a+b|=_______.www-2-1-cnjy-com
7.已知△ABC的周长是12,三边长分别为a,b,c,若b>a,b>c,则b的取值范围是_______.21*cnjy*com
8.湖边上有A,B两个村庄(如图),从A到B有两条路可走,即A→P→B和A→Q→B.请问哪条路较短,并说明理由.【版权所有:21教育】
9.已知等腰三角形一腰上的中线把这个三角形的周长分成12 cm和21 cm两部分,求这个三角形的腰长. 21教育名师原创作品
10.观察并探求下列各问题,写出你所观察得到的结论,并说明理由.
(1)如图①,在△ABC中,P为边BC上一点,试观察比较BP+PC与AB+AC的大小,并说明理由;
①
②
③
④
⑤
(2)若点P移至△ABC内,得图②,试观察比较△BPC的周长与△ABC的周长的大小,并说明理由;
(3)若点P变为两个点P1,P2,得图③,试观察比较四边形BP1P2C的周长与△ABC的周长的大小,并说明理由;21·世纪*教育网
(4)若点P1,P2移至△ABC外,并使点P1,P2与点A在边BC的异侧,且∠P1BC<∠ABC,∠P2CB<∠ACB,得图④,试观察比较四边形BP1P2C的周长与△ABC的周长的大小,并说明理由;【来源:21cnj*y.co*m】
(5)若将(3)中的四边形BP1P2C的顶点B,C移至△ABC内,得四边形B1P1P2C1,如图⑤,试观察比较四边形B1P1P2C1的周长与△ABC的周长的大小,并说明理由.21*cnjy*com
参考答案
【基础训练】
1.【答案】D
解:已知两条边长,则第三条边的长度应是大于两条边长的差而小于两条边长的和,这样就可求出第三条边长的取值范围.根据题意,得2-12.【答案】B
3.【答案】B
解:工人师傅做了一个长方形窗框ABCD,为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在E,G两点之间(没有构成三角形),这种做法根据的是三角形的稳定性.故选B.
4.【答案】三角形两边之和大于第三边(或两点之间线段最短)
5.【答案】166.解:(1)因为4k+6k>8k,所以以长为4k,6k,8k的三条线段为边能组成三角形.
(2)因为(m+1)+(m+1)=2m+2>2m,m+1+2m=3m+1>m+1,所以以长为m+1,2m,m+1的三条线段为边能组成三角形.21教育网
(3)因为a+b分析:判断三条线段能否组成三角形,关键是看三条线段是否满足任何两条线段的长度之和大于第三条线段的长度或任何两条线段的长度之差小于第三条线段的长度.但通常并不需要一一验证.其简便方法是将较短两条线段的长度之和与最长的线段的长度相比较,或将最短的线段的长度与其他两条线段的长度的差相比较.
7.解:解关于x的方程=x+1,得x=a-2.
由题意得7-3所以4解得6所以a的取值范围是68.解:因为PA+PB>AB,PA+PC>AC,PB+PC>BC,
所以PA+PB+PA+PC+PB+PC>AB+AC+BC.
所以2(PA+PB+PC)>AB+AC+BC.
即PA+PB+PC>(AB+BC+AC).
【培优提升】
1.【答案】B
解:设AB=AC=x cm,则由三角形的三边关系可得解得52.【答案】C
解:从四条线段中任选三条的所有组合:3 cm,6 cm,8 cm和3 cm,6 cm,9 cm和6 cm,8 cm,9 cm和3 cm,8 cm,9 cm;只有长为3 cm,6 cm,8 cm;6 cm,8 cm,9 cm;3 cm,8 cm,9 cm的线段能组成三角形.
3.错误答案:D
诊断:此题出错的原因在于只注意分类讨论而忽视三角形三边关系,当腰长为3时,则三角形三边长分别为3,3,7,3+3<7,不能组成三角形;当3为底边长时,此时三角形三边长分别为3,7,7,能组成三角形.故此三角形的周长为17.21cnjy.com
正确答案:A
4.【答案】C
5.【答案】1解:在△ABC中,由三角形的三边关系,得第三边长的取值范围是4-3解得1在四边形A'B'C'D'中,由三角形的三边关系,得4-3<其中一条对角线的长<4+3,即1<其中一条对角线的长<7,【出处:21教育名师】
则c'的取值范围是10-76.【答案】-a+b+3c
解:先根据三角形两边之和大于第三边,得a-b-c<0,b-c-a<0,c+b-a>0.再根据绝对值的意义,得原式=-(a-b-c)-(b-c-a)+(c-a+b)=-a+b+3c.
7.【答案】4解:因为b>a,b>c,a+c>b,所以a+b+c<3b,a+b+c>2b,得2b<12<3b,得48.解:A→Q→B这条路较短.理由如下:延长AQ交BP于E.在△APE中,AP+PE>AQ+QE①,
在△BEQ中,QE+BE>BQ②,
①+②,得AP+PE+QE+BE>AQ+QE+BQ,
即AP+BP>AQ+BQ.
9.解:如图所示.
设腰AB=x cm,底BC=y cm,D为AC边上的中点.根据题意,得x+x=12,且y+x=21;或x+x=21,且y+x=12.解得x=8,y=17;或x=14,y=5.显然当x=8,y=17时,8+8<17不满足三角形的三边关系,应舍去.故此三角形的腰长是14 cm.
10.解:(1)BP+PC(2)△BPC的周长<△ABC的周长.理由如下:
如图,延长BP交AC于M,在△ABM中,BP+PM(第10题(2))
(第10题(3))
(3)四边形BP1P2C的周长<△ABC的周长.理由如下:
如图①,分别延长BP1,CP2交于M,由(2)知,BM+CM或:作直线P1P2分别交AB,AC于M,N(如图②),在△BMP1中,BP1(4)四边形BP1P2C的周长<△ABC的周长.理由如下:将四边形BP1P2C沿直线BC翻折,使点P1,P2落在△ABC内,转化为(3)的情形即可.
(第10题(5))
(5)四边形B1P1P2C1的周长<△ABC的周长.理由如下:
如图,作直线B1P1分别交AB,BC于M,N,延长C1P2交AB于H,延长B1C1交AC于K,在△BNM中,NB1+B1P1+P1M有,B1C1+C1K
核心笔记: 1.三角形的三边关系:三角形的任何两边之和大于第三边,三角形的任何两边之差小于第三边.若已知三角形的两边长为m,n(m≥n),则第三边长x的取值范围是m-n
基础训练
1.一个三角形的三条边长分别为1,2,x,则x的取值范围是( )
A.1≤x≤3 B.1
A.1 cm,2 cm,4 cm B.4 cm,6 cm,8 cm
C.5 cm,6 cm,12 cm D.2 cm,3 cm,5 cm
3.如图,工人师傅做了一个长方形窗框ABCD,E,F,G,H分别是四条边上的中点,为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在( )21世纪教育网版权所有
A.A,C两点之间 B.E,G两点之间
C.B,F两点之间 D.G,H两点之间
4.如图,为抄近路践踏草坪是一种不文明的现象,请你用数学知识解释出现这一现象的原因: .
5.若△ABC的两边长分别为6,8,则△ABC的周长x的取值范围是________.
6.下列各组中的代数式分别表示三条线段的长度,试判断以这些线段为边能否组成三角形.
(1)4k,6k,8k(k>0);
(2)m+1,2m,m+1(m>0);
(3)a,b,a+b+1(a>0,b>0).
7.已知△ABC的两边长分别为3和7,第三边的长是关于x的方程=x+1的解,求a的取值范围.
8.如图所示,已知P是△ABC内一点.
试说明PA+PB+PC>(AB+BC+AC).
培优提升
1.在等腰三角形ABC中,AB=AC,其周长为20 cm,则AB边的取值范围是( )
A.1 cm
A.1 B.2 C.3 D.4
3.一个等腰三角形的两边长分别是3和7,则它的周长为( )
A.17 B.15 C.13 D.13或17
4.△ABC的三边长分别为a,b,c,且(a+b-c)(a-c)=0,那么△ABC中边的关系是( )2·1·c·n·j·y
A.a>b>c B.a+b=c
C.a=c D.不能确定
5.已知△ABC的三边长分别为a,b,c,若a=3,b=4,则c的取值范围是_______;已知四边形A'B'C'D'的四边长分别为a',b',c',d',若a'=3,b'=4,d'=10,则c'的取值范围是_______.【来源:21·世纪·教育·网】
6.已知a,b,c分别是三角形的三边长,化简|a-b-c|+|b-c-a|+|c-a+b|=_______.www-2-1-cnjy-com
7.已知△ABC的周长是12,三边长分别为a,b,c,若b>a,b>c,则b的取值范围是_______.21*cnjy*com
8.湖边上有A,B两个村庄(如图),从A到B有两条路可走,即A→P→B和A→Q→B.请问哪条路较短,并说明理由.【版权所有:21教育】
9.已知等腰三角形一腰上的中线把这个三角形的周长分成12 cm和21 cm两部分,求这个三角形的腰长. 21教育名师原创作品
10.观察并探求下列各问题,写出你所观察得到的结论,并说明理由.
(1)如图①,在△ABC中,P为边BC上一点,试观察比较BP+PC与AB+AC的大小,并说明理由;
①
②
③
④
⑤
(2)若点P移至△ABC内,得图②,试观察比较△BPC的周长与△ABC的周长的大小,并说明理由;
(3)若点P变为两个点P1,P2,得图③,试观察比较四边形BP1P2C的周长与△ABC的周长的大小,并说明理由;21·世纪*教育网
(4)若点P1,P2移至△ABC外,并使点P1,P2与点A在边BC的异侧,且∠P1BC<∠ABC,∠P2CB<∠ACB,得图④,试观察比较四边形BP1P2C的周长与△ABC的周长的大小,并说明理由;【来源:21cnj*y.co*m】
(5)若将(3)中的四边形BP1P2C的顶点B,C移至△ABC内,得四边形B1P1P2C1,如图⑤,试观察比较四边形B1P1P2C1的周长与△ABC的周长的大小,并说明理由.21*cnjy*com
参考答案
【基础训练】
1.【答案】D
解:已知两条边长,则第三条边的长度应是大于两条边长的差而小于两条边长的和,这样就可求出第三条边长的取值范围.根据题意,得2-1
3.【答案】B
解:工人师傅做了一个长方形窗框ABCD,为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在E,G两点之间(没有构成三角形),这种做法根据的是三角形的稳定性.故选B.
4.【答案】三角形两边之和大于第三边(或两点之间线段最短)
5.【答案】16
(2)因为(m+1)+(m+1)=2m+2>2m,m+1+2m=3m+1>m+1,所以以长为m+1,2m,m+1的三条线段为边能组成三角形.21教育网
(3)因为a+b
7.解:解关于x的方程=x+1,得x=a-2.
由题意得7-3
所以PA+PB+PA+PC+PB+PC>AB+AC+BC.
所以2(PA+PB+PC)>AB+AC+BC.
即PA+PB+PC>(AB+BC+AC).
【培优提升】
1.【答案】B
解:设AB=AC=x cm,则由三角形的三边关系可得解得5
解:从四条线段中任选三条的所有组合:3 cm,6 cm,8 cm和3 cm,6 cm,9 cm和6 cm,8 cm,9 cm和3 cm,8 cm,9 cm;只有长为3 cm,6 cm,8 cm;6 cm,8 cm,9 cm;3 cm,8 cm,9 cm的线段能组成三角形.
3.错误答案:D
诊断:此题出错的原因在于只注意分类讨论而忽视三角形三边关系,当腰长为3时,则三角形三边长分别为3,3,7,3+3<7,不能组成三角形;当3为底边长时,此时三角形三边长分别为3,7,7,能组成三角形.故此三角形的周长为17.21cnjy.com
正确答案:A
4.【答案】C
5.【答案】1
则c'的取值范围是10-7
解:先根据三角形两边之和大于第三边,得a-b-c<0,b-c-a<0,c+b-a>0.再根据绝对值的意义,得原式=-(a-b-c)-(b-c-a)+(c-a+b)=-a+b+3c.
7.【答案】4
在△BEQ中,QE+BE>BQ②,
①+②,得AP+PE+QE+BE>AQ+QE+BQ,
即AP+BP>AQ+BQ.
9.解:如图所示.
设腰AB=x cm,底BC=y cm,D为AC边上的中点.根据题意,得x+x=12,且y+x=21;或x+x=21,且y+x=12.解得x=8,y=17;或x=14,y=5.显然当x=8,y=17时,8+8<17不满足三角形的三边关系,应舍去.故此三角形的腰长是14 cm.
10.解:(1)BP+PC
如图,延长BP交AC于M,在△ABM中,BP+PM
(第10题(3))
(3)四边形BP1P2C的周长<△ABC的周长.理由如下:
如图①,分别延长BP1,CP2交于M,由(2)知,BM+CM
(第10题(5))
(5)四边形B1P1P2C1的周长<△ABC的周长.理由如下:
如图,作直线B1P1分别交AB,BC于M,N,延长C1P2交AB于H,延长B1C1交AC于K,在△BNM中,NB1+B1P1+P1M
