9.2 多边形的内角和与外角和 同步练习
文档属性
| 名称 | 9.2 多边形的内角和与外角和 同步练习 |

|
|
| 格式 | zip | ||
| 文件大小 | 427.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-16 00:00:00 | ||
图片预览


文档简介
9.2 多边形的内角和与外角和
核心笔记: 1.多边形:一般地,由n条不在同一直线上的线段首尾顺次连结组成的平面图形称为n边形,又称为多边形.www.21-cn-jy.com
2.正多边形:如果多边形的各边都相等,各内角也都相等,那么就称它为正多边形.
3.连结多边形不相邻的两个顶点的线段叫做多边形的对角线.
4.n边形的内角和为(n-2)·180°.
5.任意多边形的外角和都为360°.
基础训练
1.若一个多边形的内角和是900°,则这个多边形的边数为( )
A.5 B.6 C.7 D.8
2.从一个n边形的同一个顶点出发,分别连结这个顶点与其余各顶点,若把这个多边形分割成6个三角形,则n的值是( )
A.6 B.7 C.8 D.9
3.如果一个多边形的每一个外角都是60°,则这个多边形的边数是( )
A.3 B.4 C.5 D.6
4.一个六边形的内角和是 .
5.已知一个多边形的每一个内角都等于120°,则此多边形从一个顶点出发的对角线共有________条,可以将此多边形分成 个三角形.21·cn·jy·com
6.一个多边形截去一个角,形成一个新多边形,新多边形的内角和为2520°,则原多边形的边数是多少?
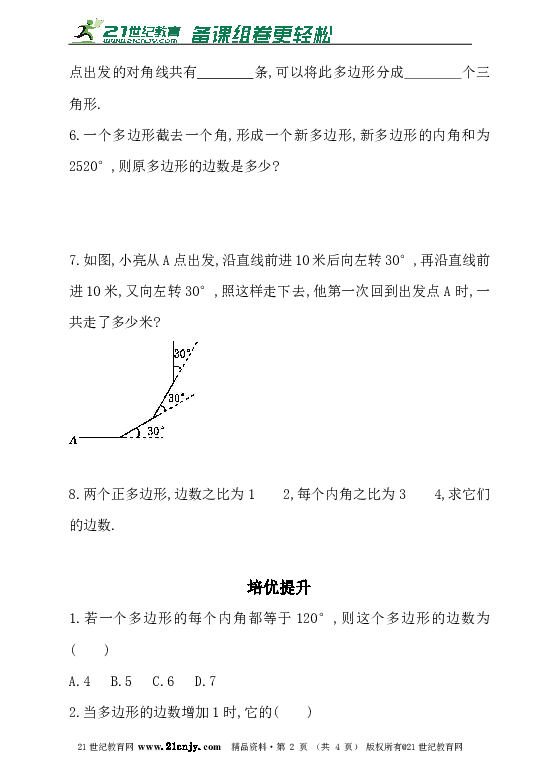
7.如图,小亮从A点出发,沿直线前进10米后向左转30°,再沿直线前进10米,又向左转30°,照这样走下去,他第一次回到出发点A时,一共走了多少米?21教育网
8.两个正多边形,边数之比为1??2,每个内角之比为3??4,求它们的边数.
培优提升
1.若一个多边形的每个内角都等于120°,则这个多边形的边数为( )
A.4 B.5 C.6 D.7
2.当多边形的边数增加1时,它的( )
A.内角和、外角和都不变
B.内角和增加180°,外角和不变
C.内角和增加180°,外角和减少180°
D.内角和、外角和都增加180°
3.已知一个多边形的内角和等于它的外角和,则这个多边形的边数为( )
A.3 B.4 C.5 D.6
4.一个多边形截去一个角后,形成另一个多边形的内角和为720°,那么原多边形的边数为( )
A.5 B.5或6
C.5或7 D.5或6或7
5.一个多边形的内角和是1440°,则这个多边形是_______边形,过其中一个顶点可以作_______条对角线,这个多边形共有_______条对角线.?2·1·c·n·j·y
6.一个多边形,若减少一条边,则内角和将会;若一个多边形减少一条边后,内角和为2 160°,则它原来的边数为_______.?
7.每个内角都相等的n边形中,每个外角等于内角的,则n=_______.
8.平面上,将边长相等的正三角形、正方形、正五边形、正六边形的一边重合并叠在一起,如图,则∠3+∠1-∠2= °.
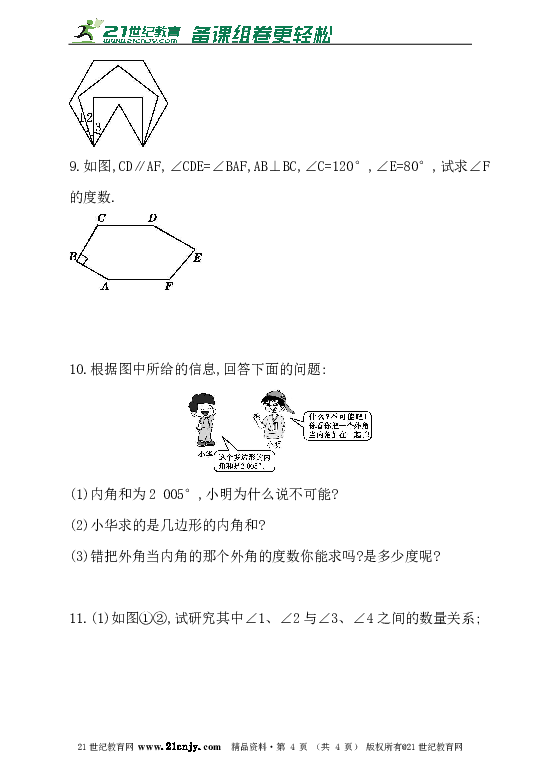
9.如图,CD∥AF,∠CDE=∠BAF,AB⊥BC,∠C=120°,∠E=80°,试求∠F的度数.21世纪教育网版权所有
10.根据图中所给的信息,回答下面的问题:
(1)内角和为2 005°,小明为什么说不可能?
(2)小华求的是几边形的内角和?
(3)错把外角当内角的那个外角的度数你能求吗?是多少度呢?
11.(1)如图①②,试研究其中∠1、∠2与∠3、∠4之间的数量关系;
(2)如果我们把∠1、∠2称为四边形的外角,那么请你用文字描述上述的关系式;
(3)用你发现的结论解决下面的问题:
如图③,AE、DE分别是四边形ABCD的外角∠NAD、∠MDA的平分线,∠B+∠C=240°,求∠E的度数.【来源:21·世纪·教育·网】
参考答案
【基础训练】
1.【答案】C
解:设这个多边形的边数为n,根据多边形的内角和公式可得(n-2)·180°=900°,解得n=7.故选C.21·世纪*教育网
2.【答案】C 3.【答案】D
4.【答案】720°
解:由多边形的内角和公式可得(6-2)×180°=720°.
5.【答案】3;4
6.解:2 520°÷180°+2=16,所以新多边形为十六边形.所以原多边形的边数为15,16或17.www-2-1-cnjy-com
7.解:∵小亮每次都是沿直线前进10米后向左转30°,
∴他走过的路线的形状是正多边形,
∴边数=360°÷30°=12,
∴他第一次回到出发点A时,一共走了
12×10=120(米).
8.解:设这两个正多边形的边数分别为n和2n,则正n边形的每个内角都为,正2n边形的每个内角都为.所以??=3??4,解得n=5.所以这两个正多边形的边数分别为5和10.2-1-c-n-j-y
【培优提升】
1.【答案】C
2.【答案】B
解:本题易错误地认为多边形的外角和随边数增加而增加,实际上任意多边形的外角和都为360°,它与边数无关,设多边形的边数为n,当边数增加1时,内角和增加(n+1-2)×180°-(n-2)×180°=180°.
3.【答案】B
4.【答案】D
解:设内角和为720°的多边形的边数是n,则(n-2)·180°=720°,解得n=6.则原多边形的边数为5或6或7.故选D.21*cnjy*com
5.【答案】10;7;35
解:设这个多边形的边数为n,根据多边形的内角和公式可得(n-2)×180°=1 440°,解方程可得n的值;根据n边形从一个顶点出发可引出(n-3)条对角线,从n个顶点出发引出n(n-3)条对角线,而每条对角线重复一次,所以n边形对角线的总条数为(n≥3,且n为整数),从而可得答案.【来源:21cnj*y.co*m】
6.【答案】减少180°;15
7.【答案】7
8.【答案】24
9.解:如图,连结AD,
在四边形ABCD中,∠BAD+∠ADC+∠B+∠C=360°.
∵AB⊥BC,
∴∠B=90°.
又∵∠C=120°,
∴∠BAD+∠ADC=150°.
∵CD∥AF,
∴∠ADC=∠DAF.
∴∠BAD+∠DAF=150°,
即∠BAF=150°,
∴∠CDE=∠BAF=150°,
在四边形ADEF中,
∠DAF+∠EDA+∠F+∠E=360°,
∴∠ADC+∠EDA+∠F+∠E=360°,
即∠CDE+∠F+∠E=360°,
∴∠F+∠E=210°.
又∵∠E=80°,
∴∠F=130°.
10.解:(1)因为2 005°不是180°的整数倍,所以小明说不可能.
(2)设小华求的是x边形的内角和.
依题意有0°<2 005°-(x-2)·180°<180°,
解得12所以多边形的边数是13,该多边形为十三边形.小华求的是十三边形的内角和.
(3)能.十三边形的内角和是(13-2)×180°=1980°,则错把外角当内角的那个外角的度数是2005°-1980°=25°.21cnjy.com
11.解:(1)∵∠3、∠4、∠5、∠6是四边形的四个内角,
∴∠3+∠4+∠5+∠6=360°,
∴∠3+∠4=360°-(∠5+∠6).
∵∠1+∠5=180°,∠2+∠6=180°,
∴∠1+∠2=360°-(∠5+∠6),
∴∠1+∠2=∠3+∠4.
(2)四边形的任意两个外角的和等于与它们不相邻的两个内角的和.
(3)∵∠B+∠C=240°,
∴∠MDA+∠NAD=240°.
∵AE、DE分别是∠NAD、∠MDA的平分线,
∴∠ADE=∠MDA,∠DAE=∠NAD,
∴∠ADE+∠DAE=(∠MDA+∠NAD)=×240°=120°,
∴∠E=180°-(∠ADE+∠DAE)=180°-120°=60°.
核心笔记: 1.多边形:一般地,由n条不在同一直线上的线段首尾顺次连结组成的平面图形称为n边形,又称为多边形.www.21-cn-jy.com
2.正多边形:如果多边形的各边都相等,各内角也都相等,那么就称它为正多边形.
3.连结多边形不相邻的两个顶点的线段叫做多边形的对角线.
4.n边形的内角和为(n-2)·180°.
5.任意多边形的外角和都为360°.
基础训练
1.若一个多边形的内角和是900°,则这个多边形的边数为( )
A.5 B.6 C.7 D.8
2.从一个n边形的同一个顶点出发,分别连结这个顶点与其余各顶点,若把这个多边形分割成6个三角形,则n的值是( )
A.6 B.7 C.8 D.9
3.如果一个多边形的每一个外角都是60°,则这个多边形的边数是( )
A.3 B.4 C.5 D.6
4.一个六边形的内角和是 .
5.已知一个多边形的每一个内角都等于120°,则此多边形从一个顶点出发的对角线共有________条,可以将此多边形分成 个三角形.21·cn·jy·com
6.一个多边形截去一个角,形成一个新多边形,新多边形的内角和为2520°,则原多边形的边数是多少?
7.如图,小亮从A点出发,沿直线前进10米后向左转30°,再沿直线前进10米,又向左转30°,照这样走下去,他第一次回到出发点A时,一共走了多少米?21教育网
8.两个正多边形,边数之比为1??2,每个内角之比为3??4,求它们的边数.
培优提升
1.若一个多边形的每个内角都等于120°,则这个多边形的边数为( )
A.4 B.5 C.6 D.7
2.当多边形的边数增加1时,它的( )
A.内角和、外角和都不变
B.内角和增加180°,外角和不变
C.内角和增加180°,外角和减少180°
D.内角和、外角和都增加180°
3.已知一个多边形的内角和等于它的外角和,则这个多边形的边数为( )
A.3 B.4 C.5 D.6
4.一个多边形截去一个角后,形成另一个多边形的内角和为720°,那么原多边形的边数为( )
A.5 B.5或6
C.5或7 D.5或6或7
5.一个多边形的内角和是1440°,则这个多边形是_______边形,过其中一个顶点可以作_______条对角线,这个多边形共有_______条对角线.?2·1·c·n·j·y
6.一个多边形,若减少一条边,则内角和将会;若一个多边形减少一条边后,内角和为2 160°,则它原来的边数为_______.?
7.每个内角都相等的n边形中,每个外角等于内角的,则n=_______.
8.平面上,将边长相等的正三角形、正方形、正五边形、正六边形的一边重合并叠在一起,如图,则∠3+∠1-∠2= °.
9.如图,CD∥AF,∠CDE=∠BAF,AB⊥BC,∠C=120°,∠E=80°,试求∠F的度数.21世纪教育网版权所有
10.根据图中所给的信息,回答下面的问题:
(1)内角和为2 005°,小明为什么说不可能?
(2)小华求的是几边形的内角和?
(3)错把外角当内角的那个外角的度数你能求吗?是多少度呢?
11.(1)如图①②,试研究其中∠1、∠2与∠3、∠4之间的数量关系;
(2)如果我们把∠1、∠2称为四边形的外角,那么请你用文字描述上述的关系式;
(3)用你发现的结论解决下面的问题:
如图③,AE、DE分别是四边形ABCD的外角∠NAD、∠MDA的平分线,∠B+∠C=240°,求∠E的度数.【来源:21·世纪·教育·网】
参考答案
【基础训练】
1.【答案】C
解:设这个多边形的边数为n,根据多边形的内角和公式可得(n-2)·180°=900°,解得n=7.故选C.21·世纪*教育网
2.【答案】C 3.【答案】D
4.【答案】720°
解:由多边形的内角和公式可得(6-2)×180°=720°.
5.【答案】3;4
6.解:2 520°÷180°+2=16,所以新多边形为十六边形.所以原多边形的边数为15,16或17.www-2-1-cnjy-com
7.解:∵小亮每次都是沿直线前进10米后向左转30°,
∴他走过的路线的形状是正多边形,
∴边数=360°÷30°=12,
∴他第一次回到出发点A时,一共走了
12×10=120(米).
8.解:设这两个正多边形的边数分别为n和2n,则正n边形的每个内角都为,正2n边形的每个内角都为.所以??=3??4,解得n=5.所以这两个正多边形的边数分别为5和10.2-1-c-n-j-y
【培优提升】
1.【答案】C
2.【答案】B
解:本题易错误地认为多边形的外角和随边数增加而增加,实际上任意多边形的外角和都为360°,它与边数无关,设多边形的边数为n,当边数增加1时,内角和增加(n+1-2)×180°-(n-2)×180°=180°.
3.【答案】B
4.【答案】D
解:设内角和为720°的多边形的边数是n,则(n-2)·180°=720°,解得n=6.则原多边形的边数为5或6或7.故选D.21*cnjy*com
5.【答案】10;7;35
解:设这个多边形的边数为n,根据多边形的内角和公式可得(n-2)×180°=1 440°,解方程可得n的值;根据n边形从一个顶点出发可引出(n-3)条对角线,从n个顶点出发引出n(n-3)条对角线,而每条对角线重复一次,所以n边形对角线的总条数为(n≥3,且n为整数),从而可得答案.【来源:21cnj*y.co*m】
6.【答案】减少180°;15
7.【答案】7
8.【答案】24
9.解:如图,连结AD,
在四边形ABCD中,∠BAD+∠ADC+∠B+∠C=360°.
∵AB⊥BC,
∴∠B=90°.
又∵∠C=120°,
∴∠BAD+∠ADC=150°.
∵CD∥AF,
∴∠ADC=∠DAF.
∴∠BAD+∠DAF=150°,
即∠BAF=150°,
∴∠CDE=∠BAF=150°,
在四边形ADEF中,
∠DAF+∠EDA+∠F+∠E=360°,
∴∠ADC+∠EDA+∠F+∠E=360°,
即∠CDE+∠F+∠E=360°,
∴∠F+∠E=210°.
又∵∠E=80°,
∴∠F=130°.
10.解:(1)因为2 005°不是180°的整数倍,所以小明说不可能.
(2)设小华求的是x边形的内角和.
依题意有0°<2 005°-(x-2)·180°<180°,
解得12
(3)能.十三边形的内角和是(13-2)×180°=1980°,则错把外角当内角的那个外角的度数是2005°-1980°=25°.21cnjy.com
11.解:(1)∵∠3、∠4、∠5、∠6是四边形的四个内角,
∴∠3+∠4+∠5+∠6=360°,
∴∠3+∠4=360°-(∠5+∠6).
∵∠1+∠5=180°,∠2+∠6=180°,
∴∠1+∠2=360°-(∠5+∠6),
∴∠1+∠2=∠3+∠4.
(2)四边形的任意两个外角的和等于与它们不相邻的两个内角的和.
(3)∵∠B+∠C=240°,
∴∠MDA+∠NAD=240°.
∵AE、DE分别是∠NAD、∠MDA的平分线,
∴∠ADE=∠MDA,∠DAE=∠NAD,
∴∠ADE+∠DAE=(∠MDA+∠NAD)=×240°=120°,
∴∠E=180°-(∠ADE+∠DAE)=180°-120°=60°.
