10.1.2 轴对称的再认识 同步练习
文档属性
| 名称 | 10.1.2 轴对称的再认识 同步练习 |

|
|
| 格式 | zip | ||
| 文件大小 | 508.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-16 00:00:00 | ||
图片预览


文档简介
10.1.2 轴对称的再认识
核心笔记: 1.垂直平分线:垂直并且平分一条线段的直线叫做这条线段的垂直平分线,垂直平分线又叫中垂线.21教育网
2.线段的对称轴是线段的垂直平分线和线段本身所在的直线.
3.角的对称轴是角平分线所在的直线.
4.如果一个图形是轴对称图形,那么连结对称点的线段的垂直平分线就是该图形的对称轴.
基础训练
1.下列说法中正确的有( )
①P是线段AB上的一点,直线l经过点P且l⊥AB,则l是线段AB的垂直平分线;
②直线l经过线段AB的中点,则l是线段AB的垂直平分线;
③经过线段AB的中点P且垂直于AB的直线l是线段AB的垂直平分线.
A.0个 B.1个
C.2个 D.3个
2.如图,正方形地砖的图案是轴对称图形,该图形的对称轴有( )
( http: / / www.21cnjy.com )
A.1条 B.2条 C.4条 D.8条
3.下列图形中,不一定是轴对称图形的是( )
A.角 B.三角形
C.线段 D.圆
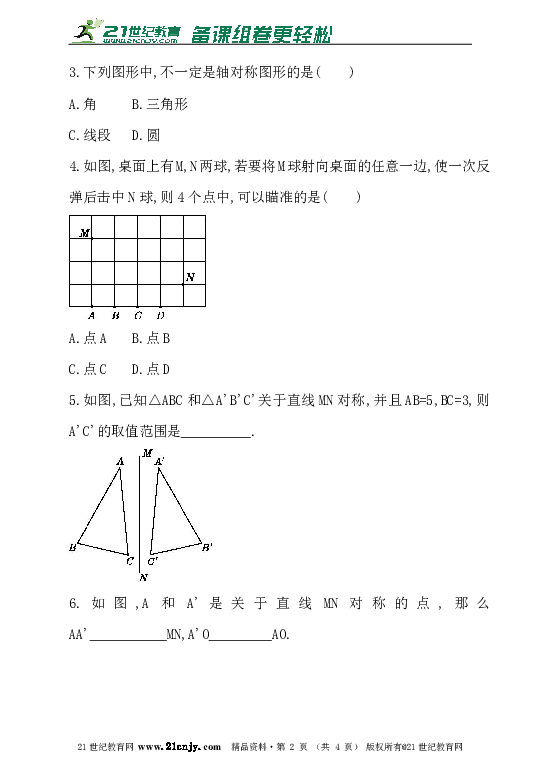
4.如图,桌面上有M,N两球,若要将M球射向桌面的任意一边,使一次反弹后击中N球,则4个点中,可以瞄准的是( )21cnjy.com
( http: / / www.21cnjy.com )
A.点A B.点B
C.点C D.点D
5.如图,已知△ABC和△A'B'C'关于直线MN对称,并且AB=5,BC=3,则A'C'的取值范围是__________.21·cn·jy·com
( http: / / www.21cnjy.com )
6.如图,A和A'是关于直线MN对称的点,那么AA'___________MN,A'O_________AO.【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com )
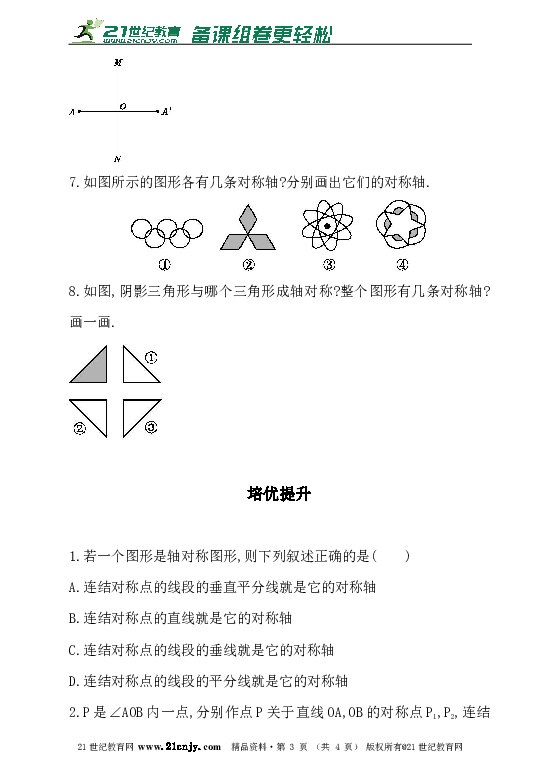
7.如图所示的图形各有几条对称轴 分别画出它们的对称轴.
( http: / / www.21cnjy.com )
8.如图,阴影三角形与哪个三角形成轴对称 整个图形有几条对称轴 画一画.
( http: / / www.21cnjy.com )
培优提升
1.若一个图形是轴对称图形,则下列叙述正确的是( )
A.连结对称点的线段的垂直平分线就是它的对称轴
B.连结对称点的直线就是它的对称轴
C.连结对称点的线段的垂线就是它的对称轴
D.连结对称点的线段的平分线就是它的对称轴
2.P是∠AOB内一点,分别作点P关于直线OA,OB的对称点P1,P2,连结OP1,OP2,则下列结论正确的是( )2·1·c·n·j·y
A.OP1⊥OP2
B.OP1=OP2
C.OP1⊥OP2且OP1=OP2
D.OP1≠OP2
3.一张四边形纸片按图①、图②依次对折后,再按图③打出一个圆形小孔,则展开铺平后的图案是( )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
4.如图所示的图形,
( http: / / www.21cnjy.com )
其中所有轴对称图形的对称轴条数之和为( )
A.13 B.11 C.10 D.8
5.按要求填写一个符合条件的图形名称.
(1)一条对称轴: ;
(2)两条对称轴: ;
(3)三条对称轴: ;
(4)四条对称轴: ;
(5)五条对称轴: ;
(6)无数条对称轴: .
6.如图,∠A=90°,E为BC上一点,A点和E点关于BD对称,B点和C点关于DE对称,求∠ABC和∠C的度数.www.21-cn-jy.com
( http: / / www.21cnjy.com )
7.如图,P在∠AOB内,点M,N分别是 ( http: / / www.21cnjy.com )点P关于AO,BO的对称点,连结MN,分别与AO,BO相交于点E,F,若△EPF的周长为15,求MN的长.
( http: / / www.21cnjy.com )
8.设直线l1和直线l2平行,且l1和l2 ( http: / / www.21cnjy.com )间的距离为a.如果线段AB在l1的右侧,并设AB关于l1的对称图形是A'B',而A'B'关于l2的对称图形是A″B″(如图),那么,线段AB和A″B″有什么关系 (注:有一组对边平行且相等的四边形是平行四边形) 21·世纪*教育网
( http: / / www.21cnjy.com )
参考答案
【基础训练】
1.【答案】B
2.【答案】C
解:如图所示,有4条对称轴.
( http: / / www.21cnjy.com )
3.【答案】B
4.【答案】D
解:如图所示,要使一次反弹后击中N球,则需要满足N球在M球反弹后经过的直线上.
5.【答案】2解:∵△ABC和△A'B'C'关于直线MN ( http: / / www.21cnjy.com )对称,∴A'C'=AC,∵AB-BC6.【答案】⊥;=
解:根据对称轴垂直平分两对称点所连线段可得出答案.
7.解:图①有1条对称轴,图②有3条对称轴,图③有8条对称轴,图④有5条对称轴.作图略.
8.解:阴影三角形与三角形①②③都分别成轴对称,整个图形有四条对称轴,如图所示.
( http: / / www.21cnjy.com )
【培优提升】
1.【答案】A
2.【答案】B
解:如图,∵点P关于直线OA,OB的对称点分别是P1,P2,
( http: / / www.21cnjy.com )
∴OP1=OP2=OP,∠ ( http: / / www.21cnjy.com )AOP=∠AOP1,∠BOP=∠BOP2,∴∠P1OP2=∠AOP+∠AOP1+∠BOP+∠BOP2=2(∠AOP+∠BOP)=2∠AOB,∵∠AOB度数任意,∴OP1⊥OP2不一定成立.故选B.21世纪教育网版权所有
3.【答案】C
4.【答案】B
解:题图中的四个图形均为轴对称图形,且对称轴的条数依次为1,2,2,6.
5.【答案】(1)直角 (2)长方形 (3)正三角形 (4)正方形
(5)正五边形 (6)圆
分析:本题是开放性题目,答案不唯一.
6.解:∵A点和E点关于BD对称,
∴∠ABD=∠EBD,
即∠ABC=2∠ABD=2∠EBD.
又B点和C点关于DE对称,
∴∠DBE=∠C,
∴∠ABC=2∠C.
∵∠A=90°,
∴∠ABC+∠C=2∠C+∠C=3∠C=90°.
∴∠C=30°,
∴∠ABC=2∠C=60°.
7.解:∵点M是点P关于AO的对称点,
∴EP=EM.
同理PF=FN.
∵MN=ME+EF+FN,
∴MN=EP+EF+PF.
∵△PEF的周长为15,
∴MN=EP+EF+PF=15.
8.解:因为l1∥l2,所以由题意易得AA'⊥l1,A'A″⊥l2,BB'⊥l1,B'B″⊥l2.
所以A″,A',A三点共线,B″,B',B三点共线.即A″A⊥l1,B″B⊥l1.
又在平面内垂直于同一条直线的两条直线互相平行,
所以AA″∥BB″.①
因为AP=PA',A'P'=P'A″,
所以AA″=2PP'=2a,
同理得BB″=2a,
所以AA″=BB″.②
由①②可知,四边形A″B″BA是平行四边形,所以线段AB平行且等于A″B″.
分析:本题考查了轴对称的性质,熟练掌握轴对称的性质是解答本题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 7 页 (共 9 页) 版权所有@21世纪教育网
核心笔记: 1.垂直平分线:垂直并且平分一条线段的直线叫做这条线段的垂直平分线,垂直平分线又叫中垂线.21教育网
2.线段的对称轴是线段的垂直平分线和线段本身所在的直线.
3.角的对称轴是角平分线所在的直线.
4.如果一个图形是轴对称图形,那么连结对称点的线段的垂直平分线就是该图形的对称轴.
基础训练
1.下列说法中正确的有( )
①P是线段AB上的一点,直线l经过点P且l⊥AB,则l是线段AB的垂直平分线;
②直线l经过线段AB的中点,则l是线段AB的垂直平分线;
③经过线段AB的中点P且垂直于AB的直线l是线段AB的垂直平分线.
A.0个 B.1个
C.2个 D.3个
2.如图,正方形地砖的图案是轴对称图形,该图形的对称轴有( )
( http: / / www.21cnjy.com )
A.1条 B.2条 C.4条 D.8条
3.下列图形中,不一定是轴对称图形的是( )
A.角 B.三角形
C.线段 D.圆
4.如图,桌面上有M,N两球,若要将M球射向桌面的任意一边,使一次反弹后击中N球,则4个点中,可以瞄准的是( )21cnjy.com
( http: / / www.21cnjy.com )
A.点A B.点B
C.点C D.点D
5.如图,已知△ABC和△A'B'C'关于直线MN对称,并且AB=5,BC=3,则A'C'的取值范围是__________.21·cn·jy·com
( http: / / www.21cnjy.com )
6.如图,A和A'是关于直线MN对称的点,那么AA'___________MN,A'O_________AO.【来源:21·世纪·教育·网】
( http: / / www.21cnjy.com )
7.如图所示的图形各有几条对称轴 分别画出它们的对称轴.
( http: / / www.21cnjy.com )
8.如图,阴影三角形与哪个三角形成轴对称 整个图形有几条对称轴 画一画.
( http: / / www.21cnjy.com )
培优提升
1.若一个图形是轴对称图形,则下列叙述正确的是( )
A.连结对称点的线段的垂直平分线就是它的对称轴
B.连结对称点的直线就是它的对称轴
C.连结对称点的线段的垂线就是它的对称轴
D.连结对称点的线段的平分线就是它的对称轴
2.P是∠AOB内一点,分别作点P关于直线OA,OB的对称点P1,P2,连结OP1,OP2,则下列结论正确的是( )2·1·c·n·j·y
A.OP1⊥OP2
B.OP1=OP2
C.OP1⊥OP2且OP1=OP2
D.OP1≠OP2
3.一张四边形纸片按图①、图②依次对折后,再按图③打出一个圆形小孔,则展开铺平后的图案是( )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
4.如图所示的图形,
( http: / / www.21cnjy.com )
其中所有轴对称图形的对称轴条数之和为( )
A.13 B.11 C.10 D.8
5.按要求填写一个符合条件的图形名称.
(1)一条对称轴: ;
(2)两条对称轴: ;
(3)三条对称轴: ;
(4)四条对称轴: ;
(5)五条对称轴: ;
(6)无数条对称轴: .
6.如图,∠A=90°,E为BC上一点,A点和E点关于BD对称,B点和C点关于DE对称,求∠ABC和∠C的度数.www.21-cn-jy.com
( http: / / www.21cnjy.com )
7.如图,P在∠AOB内,点M,N分别是 ( http: / / www.21cnjy.com )点P关于AO,BO的对称点,连结MN,分别与AO,BO相交于点E,F,若△EPF的周长为15,求MN的长.
( http: / / www.21cnjy.com )
8.设直线l1和直线l2平行,且l1和l2 ( http: / / www.21cnjy.com )间的距离为a.如果线段AB在l1的右侧,并设AB关于l1的对称图形是A'B',而A'B'关于l2的对称图形是A″B″(如图),那么,线段AB和A″B″有什么关系 (注:有一组对边平行且相等的四边形是平行四边形) 21·世纪*教育网
( http: / / www.21cnjy.com )
参考答案
【基础训练】
1.【答案】B
2.【答案】C
解:如图所示,有4条对称轴.
( http: / / www.21cnjy.com )
3.【答案】B
4.【答案】D
解:如图所示,要使一次反弹后击中N球,则需要满足N球在M球反弹后经过的直线上.
5.【答案】2
解:根据对称轴垂直平分两对称点所连线段可得出答案.
7.解:图①有1条对称轴,图②有3条对称轴,图③有8条对称轴,图④有5条对称轴.作图略.
8.解:阴影三角形与三角形①②③都分别成轴对称,整个图形有四条对称轴,如图所示.
( http: / / www.21cnjy.com )
【培优提升】
1.【答案】A
2.【答案】B
解:如图,∵点P关于直线OA,OB的对称点分别是P1,P2,
( http: / / www.21cnjy.com )
∴OP1=OP2=OP,∠ ( http: / / www.21cnjy.com )AOP=∠AOP1,∠BOP=∠BOP2,∴∠P1OP2=∠AOP+∠AOP1+∠BOP+∠BOP2=2(∠AOP+∠BOP)=2∠AOB,∵∠AOB度数任意,∴OP1⊥OP2不一定成立.故选B.21世纪教育网版权所有
3.【答案】C
4.【答案】B
解:题图中的四个图形均为轴对称图形,且对称轴的条数依次为1,2,2,6.
5.【答案】(1)直角 (2)长方形 (3)正三角形 (4)正方形
(5)正五边形 (6)圆
分析:本题是开放性题目,答案不唯一.
6.解:∵A点和E点关于BD对称,
∴∠ABD=∠EBD,
即∠ABC=2∠ABD=2∠EBD.
又B点和C点关于DE对称,
∴∠DBE=∠C,
∴∠ABC=2∠C.
∵∠A=90°,
∴∠ABC+∠C=2∠C+∠C=3∠C=90°.
∴∠C=30°,
∴∠ABC=2∠C=60°.
7.解:∵点M是点P关于AO的对称点,
∴EP=EM.
同理PF=FN.
∵MN=ME+EF+FN,
∴MN=EP+EF+PF.
∵△PEF的周长为15,
∴MN=EP+EF+PF=15.
8.解:因为l1∥l2,所以由题意易得AA'⊥l1,A'A″⊥l2,BB'⊥l1,B'B″⊥l2.
所以A″,A',A三点共线,B″,B',B三点共线.即A″A⊥l1,B″B⊥l1.
又在平面内垂直于同一条直线的两条直线互相平行,
所以AA″∥BB″.①
因为AP=PA',A'P'=P'A″,
所以AA″=2PP'=2a,
同理得BB″=2a,
所以AA″=BB″.②
由①②可知,四边形A″B″BA是平行四边形,所以线段AB平行且等于A″B″.
分析:本题考查了轴对称的性质,熟练掌握轴对称的性质是解答本题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 7 页 (共 9 页) 版权所有@21世纪教育网
