2.2.2 函数的表示法
图片预览




文档简介
课件43张PPT。第二章 §1 生活中的变量关系~§2 对函数的进一步认识2.2 函数的表示法1.掌握函数的三种表示方法:解析法、图像法、列表法.
2.会根据不同的需要选择恰当的方法表示函数.
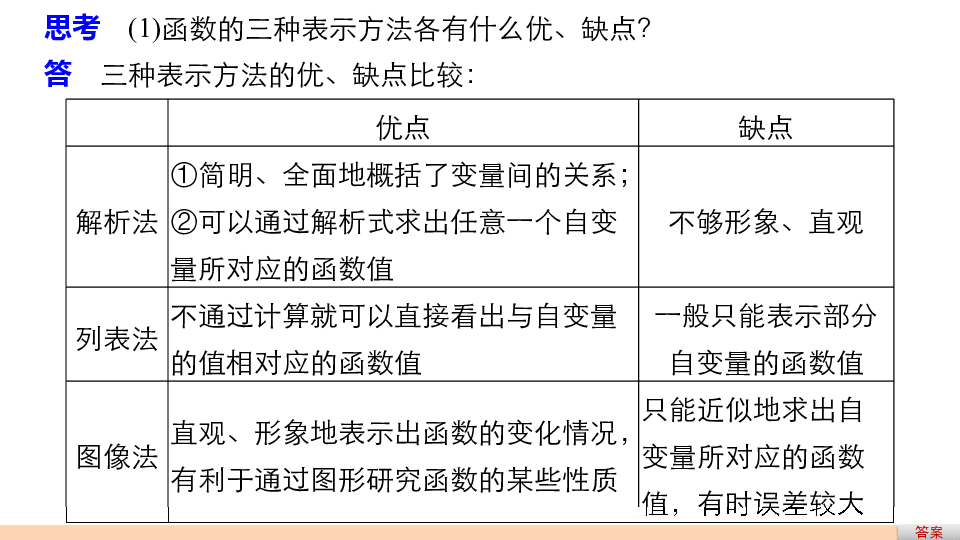
3.了解简单的分段函数,并能简单应用.学习目标知识梳理 自主学习题型探究 重点突破当堂检测 自查自纠栏目索引 知识梳理 自主学习知识点一 函数的三种表示方法答案数学表达式图像表格思考 (1)函数的三种表示方法各有什么优、缺点?答 三种表示方法的优、缺点比较:答案(2)任何一个函数都可以用解析法、列表法、图像法三种形式表示吗?答案知识点二 分段函数
有些函数在它的定义域中,对于自变量x的不同取值,对应关系也不同,这样的函数通常称为 .分段函数答案返回 题型探究 重点突破题型一 作函数的图像
例1 作出下列函数的图像:
(1)y=x+1(x∈Z);解析答案解 这个函数的图像由一些点组成,这些点都在直线y=x+1上,如图(1)所示.(2)y=x2-2x(x∈[0,3)).解析答案解 因为0≤x<3,所以这个函数的图像是抛物线y=x2-2x介于0≤x<3之间的一部分,如图(2)所示.反思与感悟1.作函数图像主要有三步:列表、描点、连线.作图像时一般应先确定函数的定义域,再在定义域内化简函数解析式,再列表画出图像.
2.函数的图像可能是平滑的曲线,也可能是一群孤立的点,画图时要注意关键点,如图像与坐标轴的交点、区间端点,二次函数的顶点等等,还要分清这些关键点是实心点还是空心点.跟踪训练1 画出下列函数的图像:
(1)y=x+1(x≤0);解析答案解 y=x+1(x≤0)表示一条射线,图像如图(1).(2)y=x2-2x(x>1,或x<-1).解析答案解 y=x2-2x=(x-1)2-1(x>1,或x<-1)是抛物线y=x2-x去掉-1
≤x≤1之间的部分后剩余曲线.如图(2).题型二 列表法表示函数
例2 已知函数f(x),g(x)分别由下表给出解析答案则f(g(1))的值为________;满足f(g(x))>g(f(x))的x的值是________.反思与感悟解析 ∵g(1)=3,
∴f(g(1))=f(3)=1.
f(g(x))与g(f(x))与x相对应的值如下表所示.反思与感悟∴f(g(x))>g(f(x))的解为x=2.答案 1 2解决此类问题关键在于弄清每个表格表示的函数.对于f(g(x))这类函数值的求解,应从内到外逐层解决,而求解不等式,则可分类讨论或列表解决.解析答案跟踪训练2 已知函数f(x),g(x)分别由下表给出(1)f(g(1))=_____;解析 由表知g(1)=3,
∴f(g(1))=f(3)=1;1解析答案(2)若g(f(x))=2,则x=______.解析 由表知g(2)=2,又g(f(x))=2,得f(x)=2,
再由表知x=1.1解析答案题型三 待定系数法求函数解析式
例3 (1)已知f(x)是一次函数,且f(f(x))=4x-1,求f(x);解 ∵f(x)是一次函数,
∴设f(x)=ax+b(a≠0),则f(f(x))=f(ax+b)=a(ax+b)+b=a2x+ab+b.
又∵f(f(x))=4x-1,
∴a2x+ab+b=4x-1,解析答案(2)已知f(x)是二次函数,且满足f(0)=1,f(x+1)-f(x)=2x,求f(x).解 ∵f(x)是二次函数,
∴设f(x)=ax2+bx+c(a≠0),
由f(0)=1,得c=1,
由f(x+1)-f(x)=2x,得a(x+1)2+b(x+1)+1-ax2-bx-1=2x.
左边展开整理得2ax+a+b=2x,∴f(x)=x2-x+1.反思与感悟跟踪训练3 已知二次函数f(x)满足f(0)=1,f(1)=2,f(2)=5,求该二次函数的解析式.解析答案解析答案解析答案=(t-1)2+1+t-1=t2-t+1.
∴所求函数的解析式为
f(x)=x2-x+1,x∈(-∞,1)∪(1,+∞).∴所求函数的解析式为f(x)=x2-x+1(x≠1).∴f(x)=x2-x+1.则x=(t-1)2,∴f(x)=x2-1(x≥1).解析答案反思与感悟解析答案跟踪训练4 已知函数f(x+1)=x2-2x,则f(x)=__________.解析 方法一 (换元法)令x+1=t,则x=t-1,可得f(t)=(t-1)2-2(t-1)=t2-4t+3,即f(x)=x2-4x+3.
方法二 (配凑法)因为x2-2x=(x2+2x+1)-(4x+4)+3=(x+1)2-4(x+1)+3,
所以f(x+1)=(x+1)2-4(x+1)+3,
即f(x)=x2-4x+3.x2-4x+3解析答案解析答案(2)若f(a)=3,求实数a的值.
解 当a≤-2时,a+1=3,
即a=2>-2,不合题意,舍去.
当-2<a<2时,a2+2a=3,即a2+2a-3=0.
∴(a-1)(a+3)=0,得a=1,或a=-3.
∵1∈(-2,2),-3?(-2,2),∴a=1符合题意.
当a≥2时,2a-1=3,即a=2符合题意.
综上可得,当f(a)=3时,a=1,或a=2.反思与感悟1.分段函数求值,一定要注意所给自变量的值所在的范围,代入相应的解析式求值.
2.已知分段函数的函数值求相对应的自变量的值,可分段利用函数解析式求得自变量的值,但应注意检验分段解析式的适用范围;也可先判断每一段上的函数值的范围,确定解析式再求解.解析答案解析 因为-2<0,所以f(-2)=-(-2)=2,
所以f(f(-2))=f(2)=22=4.C解析答案解析答案忽略函数的定义域致误易错点所以f(t)=2(t+1)2+t+1=2t2+5t+3,
所以f(x)=2x2+5x+3.所以f(t)=2(t+1)2+t+1=2t2+5t+3,
所以f(x)=2x2+5x+3(x≥-1).易错警示解析答案所以f(t)=(t-1)2-1=t2-2t(t≠1),
所以f(x)=x2-2x(x≠1).返回 当堂检测123451.已知f(x+2)=6x+5,则f(x)等于( )
A.18x+17 B.6x+5
C.6x-7 D.6x-5解析答案解析 设x+2=t,得x=t-2,
∴f(t)=6(t-2)+5=6t-7,∴f(x)=6x-7,故选C.C12345解析答案C12345解析答案3.已知函数f(x)由下表给出,则f(f(3))=________.解析 由题设给出的表知f(3)=4,则f(f(3))=f(4)=1.故填1.1123454.已知f(x)是一次函数,且满足3f(x+1)-2f(x-1)=2x+17,则f(x)的解析式为_____________.解析答案解析 设f(x)=ax+b(a≠0),
则3f(x+1)-2f(x-1)=3ax+3a+3b-2ax+2a-2b=ax+b+5a=2x+17,
所以a=2,b=7,所以f(x)=2x+7.f(x)=2x+712345答案5.如图所示,函数图像是由两条射线及抛物线的一部分组成,则函数的
解析式为_________________________.课堂小结1.函数三种表示法的优缺点2.理解分段函数应注意的问题:
(1)分段函数是一个函数,其定义域是各段“定义域”的并集,其值域是各段“值域”的并集.写定义域时,区间的端点需不重不漏.
(2)求分段函数的函数值时,自变量的取值属于哪一段,就用哪一段的解析式.
(3)研究分段函数时,应根据“先分后合”的原则,尤其是作分段函数的图像时,可先将各段的图像分别画出来,从而得到整个函数的图像.
3.求函数解析式常用的方法有(1)待定系数法;(2)换元法;(3)配凑法;(4)消元法等.返回
2.会根据不同的需要选择恰当的方法表示函数.
3.了解简单的分段函数,并能简单应用.学习目标知识梳理 自主学习题型探究 重点突破当堂检测 自查自纠栏目索引 知识梳理 自主学习知识点一 函数的三种表示方法答案数学表达式图像表格思考 (1)函数的三种表示方法各有什么优、缺点?答 三种表示方法的优、缺点比较:答案(2)任何一个函数都可以用解析法、列表法、图像法三种形式表示吗?答案知识点二 分段函数
有些函数在它的定义域中,对于自变量x的不同取值,对应关系也不同,这样的函数通常称为 .分段函数答案返回 题型探究 重点突破题型一 作函数的图像
例1 作出下列函数的图像:
(1)y=x+1(x∈Z);解析答案解 这个函数的图像由一些点组成,这些点都在直线y=x+1上,如图(1)所示.(2)y=x2-2x(x∈[0,3)).解析答案解 因为0≤x<3,所以这个函数的图像是抛物线y=x2-2x介于0≤x<3之间的一部分,如图(2)所示.反思与感悟1.作函数图像主要有三步:列表、描点、连线.作图像时一般应先确定函数的定义域,再在定义域内化简函数解析式,再列表画出图像.
2.函数的图像可能是平滑的曲线,也可能是一群孤立的点,画图时要注意关键点,如图像与坐标轴的交点、区间端点,二次函数的顶点等等,还要分清这些关键点是实心点还是空心点.跟踪训练1 画出下列函数的图像:
(1)y=x+1(x≤0);解析答案解 y=x+1(x≤0)表示一条射线,图像如图(1).(2)y=x2-2x(x>1,或x<-1).解析答案解 y=x2-2x=(x-1)2-1(x>1,或x<-1)是抛物线y=x2-x去掉-1
≤x≤1之间的部分后剩余曲线.如图(2).题型二 列表法表示函数
例2 已知函数f(x),g(x)分别由下表给出解析答案则f(g(1))的值为________;满足f(g(x))>g(f(x))的x的值是________.反思与感悟解析 ∵g(1)=3,
∴f(g(1))=f(3)=1.
f(g(x))与g(f(x))与x相对应的值如下表所示.反思与感悟∴f(g(x))>g(f(x))的解为x=2.答案 1 2解决此类问题关键在于弄清每个表格表示的函数.对于f(g(x))这类函数值的求解,应从内到外逐层解决,而求解不等式,则可分类讨论或列表解决.解析答案跟踪训练2 已知函数f(x),g(x)分别由下表给出(1)f(g(1))=_____;解析 由表知g(1)=3,
∴f(g(1))=f(3)=1;1解析答案(2)若g(f(x))=2,则x=______.解析 由表知g(2)=2,又g(f(x))=2,得f(x)=2,
再由表知x=1.1解析答案题型三 待定系数法求函数解析式
例3 (1)已知f(x)是一次函数,且f(f(x))=4x-1,求f(x);解 ∵f(x)是一次函数,
∴设f(x)=ax+b(a≠0),则f(f(x))=f(ax+b)=a(ax+b)+b=a2x+ab+b.
又∵f(f(x))=4x-1,
∴a2x+ab+b=4x-1,解析答案(2)已知f(x)是二次函数,且满足f(0)=1,f(x+1)-f(x)=2x,求f(x).解 ∵f(x)是二次函数,
∴设f(x)=ax2+bx+c(a≠0),
由f(0)=1,得c=1,
由f(x+1)-f(x)=2x,得a(x+1)2+b(x+1)+1-ax2-bx-1=2x.
左边展开整理得2ax+a+b=2x,∴f(x)=x2-x+1.反思与感悟跟踪训练3 已知二次函数f(x)满足f(0)=1,f(1)=2,f(2)=5,求该二次函数的解析式.解析答案解析答案解析答案=(t-1)2+1+t-1=t2-t+1.
∴所求函数的解析式为
f(x)=x2-x+1,x∈(-∞,1)∪(1,+∞).∴所求函数的解析式为f(x)=x2-x+1(x≠1).∴f(x)=x2-x+1.则x=(t-1)2,∴f(x)=x2-1(x≥1).解析答案反思与感悟解析答案跟踪训练4 已知函数f(x+1)=x2-2x,则f(x)=__________.解析 方法一 (换元法)令x+1=t,则x=t-1,可得f(t)=(t-1)2-2(t-1)=t2-4t+3,即f(x)=x2-4x+3.
方法二 (配凑法)因为x2-2x=(x2+2x+1)-(4x+4)+3=(x+1)2-4(x+1)+3,
所以f(x+1)=(x+1)2-4(x+1)+3,
即f(x)=x2-4x+3.x2-4x+3解析答案解析答案(2)若f(a)=3,求实数a的值.
解 当a≤-2时,a+1=3,
即a=2>-2,不合题意,舍去.
当-2<a<2时,a2+2a=3,即a2+2a-3=0.
∴(a-1)(a+3)=0,得a=1,或a=-3.
∵1∈(-2,2),-3?(-2,2),∴a=1符合题意.
当a≥2时,2a-1=3,即a=2符合题意.
综上可得,当f(a)=3时,a=1,或a=2.反思与感悟1.分段函数求值,一定要注意所给自变量的值所在的范围,代入相应的解析式求值.
2.已知分段函数的函数值求相对应的自变量的值,可分段利用函数解析式求得自变量的值,但应注意检验分段解析式的适用范围;也可先判断每一段上的函数值的范围,确定解析式再求解.解析答案解析 因为-2<0,所以f(-2)=-(-2)=2,
所以f(f(-2))=f(2)=22=4.C解析答案解析答案忽略函数的定义域致误易错点所以f(t)=2(t+1)2+t+1=2t2+5t+3,
所以f(x)=2x2+5x+3.所以f(t)=2(t+1)2+t+1=2t2+5t+3,
所以f(x)=2x2+5x+3(x≥-1).易错警示解析答案所以f(t)=(t-1)2-1=t2-2t(t≠1),
所以f(x)=x2-2x(x≠1).返回 当堂检测123451.已知f(x+2)=6x+5,则f(x)等于( )
A.18x+17 B.6x+5
C.6x-7 D.6x-5解析答案解析 设x+2=t,得x=t-2,
∴f(t)=6(t-2)+5=6t-7,∴f(x)=6x-7,故选C.C12345解析答案C12345解析答案3.已知函数f(x)由下表给出,则f(f(3))=________.解析 由题设给出的表知f(3)=4,则f(f(3))=f(4)=1.故填1.1123454.已知f(x)是一次函数,且满足3f(x+1)-2f(x-1)=2x+17,则f(x)的解析式为_____________.解析答案解析 设f(x)=ax+b(a≠0),
则3f(x+1)-2f(x-1)=3ax+3a+3b-2ax+2a-2b=ax+b+5a=2x+17,
所以a=2,b=7,所以f(x)=2x+7.f(x)=2x+712345答案5.如图所示,函数图像是由两条射线及抛物线的一部分组成,则函数的
解析式为_________________________.课堂小结1.函数三种表示法的优缺点2.理解分段函数应注意的问题:
(1)分段函数是一个函数,其定义域是各段“定义域”的并集,其值域是各段“值域”的并集.写定义域时,区间的端点需不重不漏.
(2)求分段函数的函数值时,自变量的取值属于哪一段,就用哪一段的解析式.
(3)研究分段函数时,应根据“先分后合”的原则,尤其是作分段函数的图像时,可先将各段的图像分别画出来,从而得到整个函数的图像.
3.求函数解析式常用的方法有(1)待定系数法;(2)换元法;(3)配凑法;(4)消元法等.返回
