2.3 函数的单调性
图片预览




文档简介
课件37张PPT。§3 函数的单调性第二章 函 数1.了解函数单调性的概念,掌握判断简单函数单调性的方法.
2.能用文字语言和数学符号语言描述增函数、减函数、单调性等概念,能准确理解这些定义的本质特点.学习目标知识梳理 自主学习题型探究 重点突破当堂检测 自查自纠栏目索引 知识梳理 自主学习知识点一 增函数与减函数的定义
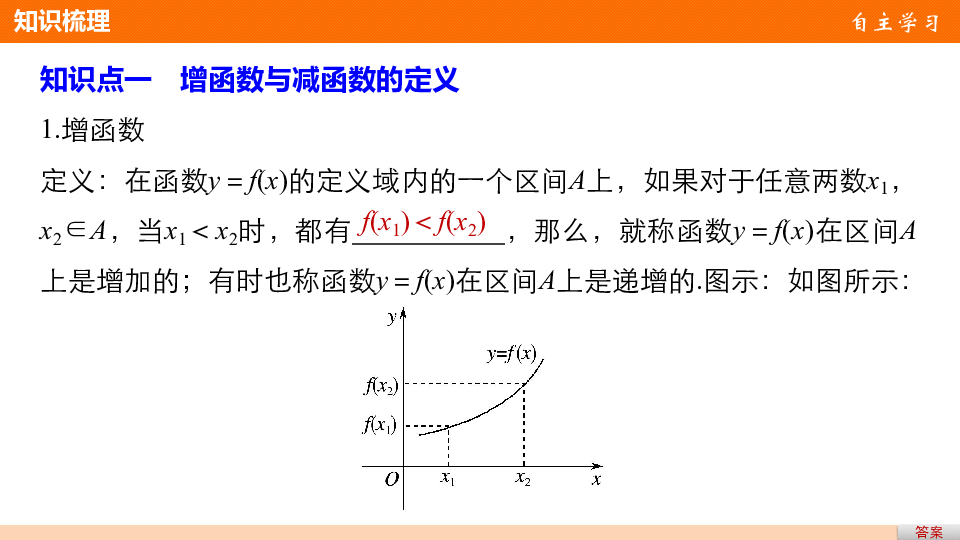
1.增函数
定义:在函数y=f(x)的定义域内的一个区间A上,如果对于任意两数x1,x2∈A,当x1<x2时,都有 ,那么,就称函数y=f(x)在区间A上是增加的;有时也称函数y=f(x)在区间A上是递增的.图示:如图所示:答案f(x1)<f(x2)答案2.减函数
定义:在函数y=f(x)的定义域内的一个区间A上,如果对于任意两数x1,x2∈A,当x1<x2时,都有 ,那么,就称函数y=f(x)在区间A上是减少的,有时也称函数y=f(x)在区间A上是递减的.
图示:如图所示.f(x1)>f(x2)知识点二 函数的单调区间与单调性
(1)如果y=f(x)在区间A上是增加的或减少的,那么称A为 .
(2)定义:如果函数y=f(x)在定义域的某个子集上是 或 ,那么就称y=f(x)在这个子集上具有单调性.
如果函数y=f(x)在 是增加的或减少的,分别称这个函数为增函数或减函数,统称为单调函数.答案单调区间增加的减少的整个定义域内思考1 若函数f(x)在定义域内的两个区间D1,D2上都是减函数,那么f(x)的减区间能写成D1∪D2吗?答案思考2 任何函数在定义域上都具有单调性吗?答案返回 题型探究 重点突破题型一 求函数的单调区间
例1 (1)如图所示的是定义在区间[-5,5]上的函数y=f(x)的图像,则函数的单调递减区间是________、________,在区间________、________上是增函数.解析答案解析 观察图像可知,y=f(x)的单调区间有[-5,-2],[-2,1],[1,3],[3,5].其中y=f(x)在区间[-5,-2],[1,3]上是增函数,在区间[-2,1],[3,5]上是减函数.
答案 [-2,1] [3,5] [-5,-2] [1,3]解析答案(-∞,1),(1,+∞)解析答案反思与感悟例2 画出函数y=-x2+2|x|+1的图像并写出函数的单调区间.函数的大致图像如图所示,单调增区间为(-∞,-1],[0,1],单调减区间为[-1,0],[1,+∞).1.作出函数的图像,利用图形的直观性能快速判断函数的单调区间,但要注意图像一定要画准确.
2.函数的单调区间是函数定义域的子集,在求解的过程中不要忽略了函数的定义域.
3.一个函数出现两个或两个以上的单调区间时,不能用“∪”连接两个单调区间,而要用“和”或“,”连接.反思与感悟解析答案由图像可知:函数的单调递减区间为(-∞,1]和(1,2];
单调递增区间为[2,+∞).?解析答案反思与感悟解析答案证明 设任意的x1,x2∈(0,1),且x1所以x1x2-1<0,x1x2>0,x2-x1>0,反思与感悟利用定义证明函数单调性的步骤如下:(1)取值:设x1,x2是该区间内的任意两个值,且x1(4)结论:根据f(x1)-f(x2)的符号及定义判断单调性.反思与感悟解析答案证明 任取x1,x2∈(-1,+∞),且x1<x2.∵x2>x1>-1,
∴x2-x1>0,(x1+1)(x2+1)>0,
∴f(x1)-f(x2)>0,即f(x1)>f(x2),
∴函数f(x)在(-1,+∞)上为减函数.解析答案题型三 函数单调性的简单应用
例4 已知函数f(x)=x2+2(a-1)x+2在区间(-∞,4]上是减函数,求实数a的取值范围.
解 ∵f(x)=x2-2(1-a)x+2
=[x-(1-a)]2+2-(1-a)2,
∴f(x)的减区间是(-∞,1-a].
∵f(x)在(-∞,4]上是减函数,
∴对称轴x=1-a必须在直线x=4的右侧或与其重合.
∴1-a≥4,解得a≤-3.反思与感悟1.二次函数是常见函数,遇到二次函数后就配方找对称轴,画出图像,会给研究问题带来很大的方便.
2.已知函数单调性求参数的取值范围,要注意数形结合,采用逆向思维方法.反思与感悟跟踪训练3 函数f(x)=-x2+2ax+1在(-∞,2)上是增函数,则实数a的取值范围是________.解析答案解析 f(x)=-x2+2ax+1=-(x-a)2+1+a2,抛物线开口向下,对称轴x=a≥2时,f(x)在(-∞,2)上是增函数,所以实数a的取值范围是a≥2.a≥2解析答案忽视函数定义域致误易错点例5 已知y=f(x)在定义域(-1,1)上是减函数,且f(1-a)且f(1-a)又f(x)在(-1,1)上是减函数,
且f(1-a)则a的取值范围是________.解析答案返回 当堂检测12345解析答案12345当a所以函数f(x)是R上的增函数.
答案 B123452.函数y=x2-6x的减区间是( )
A.(-∞,2] B.[2,+∞)
C.[3,+∞) D.(-∞,3]解析 y=x2-6x=(x-3)2-9,故减区间为(-∞,3].D解析答案12345??A解析答案123454.已知函数f(x)是(-∞,+∞)上的增函数,若a∈R,则( )
A.f(a)>f(2a) B.f(a2)C.f(a+3)>f(a-2) D.f(6)>f(a)解析答案解析 因为函数f(x)是增函数,且a+3>a-2,
所以f(a+3)>f(a-2).C123455.函数y=x|x-1|的单调递增区间是_____________________.解析答案课堂小结1.对函数单调性的理解
(1)单调性是与“区间”紧密相关的概念,一个函数在定义域的不同的区间上可以有不同的单调性.
(2)单调性是函数在某一区间上的“整体”性质,因此定义中的x1、x2有以下几个特征:一是任意性,即任意取x1,x2,“任意”二字绝不能丢掉,证明单调性时更不可随意以两个特殊值替换;二是有大小,通常规定x1(3)单调性能使自变量取值之间的不等关系和函数值的不等关系正逆互推,即由f(x)是增(减)函数且f(x1)x2).
(4)并不是所有函数都具有单调性.若一个函数在定义区间上既有增区间又有减区间,则此函数在这个区间上不存在单调性.2.单调性的证明方法
证明f(x)在区间D上的单调性应按以下步骤:
(1)设元:设x1、x2∈D且x1(2)作差:将函数值f(x1)与f(x2)作差;
(3)变形:将上述差式(因式分解、配方等)变形;
(4)判号:对上述变形的结果的正、负加以判断;
(5)定论:对f(x)的单调性作出结论.其中变形为难点,变形一定要到位,即变形到能简单明了的判断符号的形式为止,切忌变形不到位就定号.3.单调性的判断方法
(1)定义法:利用定义严格判断.
(2)图像法:作出函数的图像,用数形结合的方法确定函数的单调区间.
(3)用两个函数和(差)的单调性的规律判断:“增+增=增”,“减+减=减”,“增-减=增”,“减-增=减”.返回
2.能用文字语言和数学符号语言描述增函数、减函数、单调性等概念,能准确理解这些定义的本质特点.学习目标知识梳理 自主学习题型探究 重点突破当堂检测 自查自纠栏目索引 知识梳理 自主学习知识点一 增函数与减函数的定义
1.增函数
定义:在函数y=f(x)的定义域内的一个区间A上,如果对于任意两数x1,x2∈A,当x1<x2时,都有 ,那么,就称函数y=f(x)在区间A上是增加的;有时也称函数y=f(x)在区间A上是递增的.图示:如图所示:答案f(x1)<f(x2)答案2.减函数
定义:在函数y=f(x)的定义域内的一个区间A上,如果对于任意两数x1,x2∈A,当x1<x2时,都有 ,那么,就称函数y=f(x)在区间A上是减少的,有时也称函数y=f(x)在区间A上是递减的.
图示:如图所示.f(x1)>f(x2)知识点二 函数的单调区间与单调性
(1)如果y=f(x)在区间A上是增加的或减少的,那么称A为 .
(2)定义:如果函数y=f(x)在定义域的某个子集上是 或 ,那么就称y=f(x)在这个子集上具有单调性.
如果函数y=f(x)在 是增加的或减少的,分别称这个函数为增函数或减函数,统称为单调函数.答案单调区间增加的减少的整个定义域内思考1 若函数f(x)在定义域内的两个区间D1,D2上都是减函数,那么f(x)的减区间能写成D1∪D2吗?答案思考2 任何函数在定义域上都具有单调性吗?答案返回 题型探究 重点突破题型一 求函数的单调区间
例1 (1)如图所示的是定义在区间[-5,5]上的函数y=f(x)的图像,则函数的单调递减区间是________、________,在区间________、________上是增函数.解析答案解析 观察图像可知,y=f(x)的单调区间有[-5,-2],[-2,1],[1,3],[3,5].其中y=f(x)在区间[-5,-2],[1,3]上是增函数,在区间[-2,1],[3,5]上是减函数.
答案 [-2,1] [3,5] [-5,-2] [1,3]解析答案(-∞,1),(1,+∞)解析答案反思与感悟例2 画出函数y=-x2+2|x|+1的图像并写出函数的单调区间.函数的大致图像如图所示,单调增区间为(-∞,-1],[0,1],单调减区间为[-1,0],[1,+∞).1.作出函数的图像,利用图形的直观性能快速判断函数的单调区间,但要注意图像一定要画准确.
2.函数的单调区间是函数定义域的子集,在求解的过程中不要忽略了函数的定义域.
3.一个函数出现两个或两个以上的单调区间时,不能用“∪”连接两个单调区间,而要用“和”或“,”连接.反思与感悟解析答案由图像可知:函数的单调递减区间为(-∞,1]和(1,2];
单调递增区间为[2,+∞).?解析答案反思与感悟解析答案证明 设任意的x1,x2∈(0,1),且x1
∴x2-x1>0,(x1+1)(x2+1)>0,
∴f(x1)-f(x2)>0,即f(x1)>f(x2),
∴函数f(x)在(-1,+∞)上为减函数.解析答案题型三 函数单调性的简单应用
例4 已知函数f(x)=x2+2(a-1)x+2在区间(-∞,4]上是减函数,求实数a的取值范围.
解 ∵f(x)=x2-2(1-a)x+2
=[x-(1-a)]2+2-(1-a)2,
∴f(x)的减区间是(-∞,1-a].
∵f(x)在(-∞,4]上是减函数,
∴对称轴x=1-a必须在直线x=4的右侧或与其重合.
∴1-a≥4,解得a≤-3.反思与感悟1.二次函数是常见函数,遇到二次函数后就配方找对称轴,画出图像,会给研究问题带来很大的方便.
2.已知函数单调性求参数的取值范围,要注意数形结合,采用逆向思维方法.反思与感悟跟踪训练3 函数f(x)=-x2+2ax+1在(-∞,2)上是增函数,则实数a的取值范围是________.解析答案解析 f(x)=-x2+2ax+1=-(x-a)2+1+a2,抛物线开口向下,对称轴x=a≥2时,f(x)在(-∞,2)上是增函数,所以实数a的取值范围是a≥2.a≥2解析答案忽视函数定义域致误易错点例5 已知y=f(x)在定义域(-1,1)上是减函数,且f(1-a)
且f(1-a)
答案 B123452.函数y=x2-6x的减区间是( )
A.(-∞,2] B.[2,+∞)
C.[3,+∞) D.(-∞,3]解析 y=x2-6x=(x-3)2-9,故减区间为(-∞,3].D解析答案12345??A解析答案123454.已知函数f(x)是(-∞,+∞)上的增函数,若a∈R,则( )
A.f(a)>f(2a) B.f(a2)
所以f(a+3)>f(a-2).C123455.函数y=x|x-1|的单调递增区间是_____________________.解析答案课堂小结1.对函数单调性的理解
(1)单调性是与“区间”紧密相关的概念,一个函数在定义域的不同的区间上可以有不同的单调性.
(2)单调性是函数在某一区间上的“整体”性质,因此定义中的x1、x2有以下几个特征:一是任意性,即任意取x1,x2,“任意”二字绝不能丢掉,证明单调性时更不可随意以两个特殊值替换;二是有大小,通常规定x1
(4)并不是所有函数都具有单调性.若一个函数在定义区间上既有增区间又有减区间,则此函数在这个区间上不存在单调性.2.单调性的证明方法
证明f(x)在区间D上的单调性应按以下步骤:
(1)设元:设x1、x2∈D且x1
(3)变形:将上述差式(因式分解、配方等)变形;
(4)判号:对上述变形的结果的正、负加以判断;
(5)定论:对f(x)的单调性作出结论.其中变形为难点,变形一定要到位,即变形到能简单明了的判断符号的形式为止,切忌变形不到位就定号.3.单调性的判断方法
(1)定义法:利用定义严格判断.
(2)图像法:作出函数的图像,用数形结合的方法确定函数的单调区间.
(3)用两个函数和(差)的单调性的规律判断:“增+增=增”,“减+减=减”,“增-减=增”,“减-增=减”.返回
