第18章 平行四边形 单元试题(含答案)
文档属性
| 名称 | 第18章 平行四边形 单元试题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 194.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-17 16:11:43 | ||
图片预览


文档简介
《平行四边形》单元测试题
一、选择题(每题3分36分)
1、.矩形、菱形、正方形都具有的性质是( )
A.每一条对角线平分一组对角
B.对角线相等
C.对角线互相平分
D.对角线互相垂直
2、有下列四个命题,其中正确的个数为(
)
①两条对角线互相平分的四边形是平行四边形②两条对角线相等的四边形是菱形③两条对角线互相垂直的四边形是正方形④两条对角线相等且互相垂直的四边形是正方形
A.4
B.3
C.2
D.1
3、如图,已知AB=DC,AD=BC,E、F在DB上两点且BF=DE,若∠AEB=120°,∠ADB=30°,则∠BCF=(
)
A.150°
B.40°
C.80°
D.90°
4、若平行四边形的一边和一条对角线长都是10cm,则另一条对角线长可以是(
)
A.5cm
B.10cm
C.20cm
D.30cm
5、如图,在□ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC
的延长线于点F,BG⊥AE于G,BG=,则梯形AECD的周长为(
)
A.22
B.23
C.24
D.25
6、已知一个平行四边形两邻边的长分别为10和6,那么它的周长为(
).
A.
16
B.
60
C.32
D.
30
7、
菱形的两条对角线长分别6㎝和8㎝,则这个菱形的面积为(
)
A
.48
B.
C.
D.18
8、若四边形的两条对角线相等,则顺次连接该四边形各边中点所得的四边形是(
)
A.梯形
B.矩形
C.菱形
D.正方形
9、如图,两个平行四边形的面积分别为18、12,两阴影部分的面积分别为a、b(a>b),则(a-b)等于(
)
A.4
B.5
C.6
D.7
10、如图,平行四边形ABCD中,BC=BD,∠C=74°,则∠ADB的度数是(
)
A.16°
B.22°
C.32°
D.68°
11、如图,□的周长是,△ABC的周长是,则的长为(
)
A.
B.
C.
D.
12、如图,在□中,,,的垂直平分线交于点,则△的周长是(
)
A.6
B.8
C.9
D.10
二、填空题(每题3分)
13、直角三角形中,两直角边长分别为12和5,则斜边中线长是
__________.
14、矩形、菱形、正方形都是特殊的四边形,它们具有很多共性,如:_______(填一条即可)
15、一个平行四边形的一边长是8,一条对角线长是6,则它的另一条对角线x的取值范围为____________.
16、一个平行四边形的周长为70cm,两边的差是10cm,则平行四边形各边长___________cm。
17、如图,在平行四边形ABCD中,已知AD=9㎝,AB=5㎝,AE平分∠BAD交BC边于点E,则EC的长为___________
18、如图,在□ABCD
中,EF经过对角线的交点O,交AB于点E,交CD于点F.若AB=5,AD=4,OF=1.8,那么四边形BCFE的周长为
_____________.
三、解答题
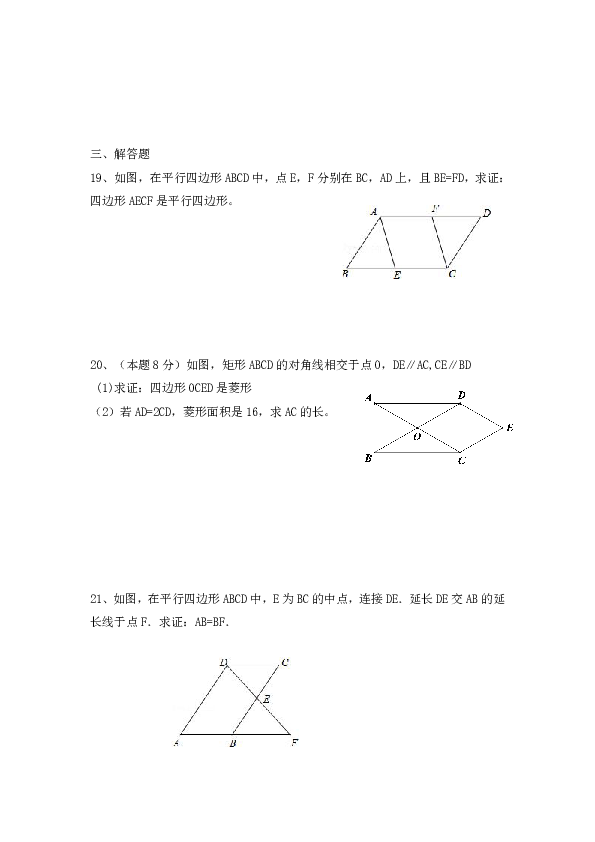
19、如图,在平行四边形ABCD中,点E,F分别在BC,AD上,且BE=FD,求证:四边形AECF是平行四边形。
20、(本题8分)如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD
(1)求证:四边形OCED是菱形
(2)若AD=2CD,菱形面积是16,求AC的长。
21、如图,在平行四边形ABCD中,E为BC的中点,连接DE.延长DE交AB的延长线于点F.求证:AB=BF.
22、如图,平行四边形ABCD,E、F两点在对角线BD上,且BE=DF,连接AE,EC,CF,FA.求证:四边形AECF是平行四边形.
23、(本题10分)如图,在△ACD中,AD=9,CD=,△ABC中,AB=AC.
如图1,若∠CAB=60°,∠ADC=30°,在△ACD外作等边△ADD′
①求证:BD=CD′
②求BD的长。
如图2,若∠CAB=90°,∠ADC=45°,求BD的长
参考答案
一、选择题
1、C
2、C
3、A.
4、D.
5、C.
6、C.
7、B
8、C
9、B
10、B
11、A
12、B
二、填空题
13、
14、4
15、7
16、35
17、4cm
18、16
15、10<x<22.
16、22.5cm,12.5cm,22.5cm,12.5cm.
17、5cm
18、26.
三、解答题
19、略
20、(1)略4分
(2)AC=
21、证明:由ABCD是平行四边形得AB∥CD,
∴∠CDE=∠F,∠C=∠EBF.
又∵E为BC的中点,
∴△DEC≌△FEB,
∴DC=FB.
又∵AB=CD,
∴AB=BF.
22、证明:连接AC交BD于点O,
∵四边形ABCD为平行四边形,
∴OA=OC,OB=OD.
∵BE=DF,∴OE=OF.
∴四边形AECF为平行四边形.
23、.(1)证△BAD≌△CAD′
②
BD=CD′=
(2)
过点A作AE⊥AD,AE=AD
证△BAD≌△CAE
BD=CE=
一、选择题(每题3分36分)
1、.矩形、菱形、正方形都具有的性质是( )
A.每一条对角线平分一组对角
B.对角线相等
C.对角线互相平分
D.对角线互相垂直
2、有下列四个命题,其中正确的个数为(
)
①两条对角线互相平分的四边形是平行四边形②两条对角线相等的四边形是菱形③两条对角线互相垂直的四边形是正方形④两条对角线相等且互相垂直的四边形是正方形
A.4
B.3
C.2
D.1
3、如图,已知AB=DC,AD=BC,E、F在DB上两点且BF=DE,若∠AEB=120°,∠ADB=30°,则∠BCF=(
)
A.150°
B.40°
C.80°
D.90°
4、若平行四边形的一边和一条对角线长都是10cm,则另一条对角线长可以是(
)
A.5cm
B.10cm
C.20cm
D.30cm
5、如图,在□ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC
的延长线于点F,BG⊥AE于G,BG=,则梯形AECD的周长为(
)
A.22
B.23
C.24
D.25
6、已知一个平行四边形两邻边的长分别为10和6,那么它的周长为(
).
A.
16
B.
60
C.32
D.
30
7、
菱形的两条对角线长分别6㎝和8㎝,则这个菱形的面积为(
)
A
.48
B.
C.
D.18
8、若四边形的两条对角线相等,则顺次连接该四边形各边中点所得的四边形是(
)
A.梯形
B.矩形
C.菱形
D.正方形
9、如图,两个平行四边形的面积分别为18、12,两阴影部分的面积分别为a、b(a>b),则(a-b)等于(
)
A.4
B.5
C.6
D.7
10、如图,平行四边形ABCD中,BC=BD,∠C=74°,则∠ADB的度数是(
)
A.16°
B.22°
C.32°
D.68°
11、如图,□的周长是,△ABC的周长是,则的长为(
)
A.
B.
C.
D.
12、如图,在□中,,,的垂直平分线交于点,则△的周长是(
)
A.6
B.8
C.9
D.10
二、填空题(每题3分)
13、直角三角形中,两直角边长分别为12和5,则斜边中线长是
__________.
14、矩形、菱形、正方形都是特殊的四边形,它们具有很多共性,如:_______(填一条即可)
15、一个平行四边形的一边长是8,一条对角线长是6,则它的另一条对角线x的取值范围为____________.
16、一个平行四边形的周长为70cm,两边的差是10cm,则平行四边形各边长___________cm。
17、如图,在平行四边形ABCD中,已知AD=9㎝,AB=5㎝,AE平分∠BAD交BC边于点E,则EC的长为___________
18、如图,在□ABCD
中,EF经过对角线的交点O,交AB于点E,交CD于点F.若AB=5,AD=4,OF=1.8,那么四边形BCFE的周长为
_____________.
三、解答题
19、如图,在平行四边形ABCD中,点E,F分别在BC,AD上,且BE=FD,求证:四边形AECF是平行四边形。
20、(本题8分)如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD
(1)求证:四边形OCED是菱形
(2)若AD=2CD,菱形面积是16,求AC的长。
21、如图,在平行四边形ABCD中,E为BC的中点,连接DE.延长DE交AB的延长线于点F.求证:AB=BF.
22、如图,平行四边形ABCD,E、F两点在对角线BD上,且BE=DF,连接AE,EC,CF,FA.求证:四边形AECF是平行四边形.
23、(本题10分)如图,在△ACD中,AD=9,CD=,△ABC中,AB=AC.
如图1,若∠CAB=60°,∠ADC=30°,在△ACD外作等边△ADD′
①求证:BD=CD′
②求BD的长。
如图2,若∠CAB=90°,∠ADC=45°,求BD的长
参考答案
一、选择题
1、C
2、C
3、A.
4、D.
5、C.
6、C.
7、B
8、C
9、B
10、B
11、A
12、B
二、填空题
13、
14、4
15、7
16、35
17、4cm
18、16
15、10<x<22.
16、22.5cm,12.5cm,22.5cm,12.5cm.
17、5cm
18、26.
三、解答题
19、略
20、(1)略4分
(2)AC=
21、证明:由ABCD是平行四边形得AB∥CD,
∴∠CDE=∠F,∠C=∠EBF.
又∵E为BC的中点,
∴△DEC≌△FEB,
∴DC=FB.
又∵AB=CD,
∴AB=BF.
22、证明:连接AC交BD于点O,
∵四边形ABCD为平行四边形,
∴OA=OC,OB=OD.
∵BE=DF,∴OE=OF.
∴四边形AECF为平行四边形.
23、.(1)证△BAD≌△CAD′
②
BD=CD′=
(2)
过点A作AE⊥AD,AE=AD
证△BAD≌△CAE
BD=CE=
