3.5.1 对数函数的图像与性质

课件36张PPT。第三章　§5 对数函数第1课时　对数函数的图像与性质1.掌握对数函数的概念.
2.理解并掌握对数函数与指数函数的关系.
3.会画具体的对数函数的图像.学习目标知识梳理 自主学习题型探究 重点突破当堂检测 自查自纠栏目索引 知识梳理 自主学习知识点一　对数函数的概念
一般地，把函数 叫作对数函数，其中 是自变量，函数的定义域是 .
思考　根据对数函数的定义，你能总结出对数函数具有哪些特点吗？
答　(1)底数a>0，且a≠1.
(2)自变量x在真数位置上，且x>0.
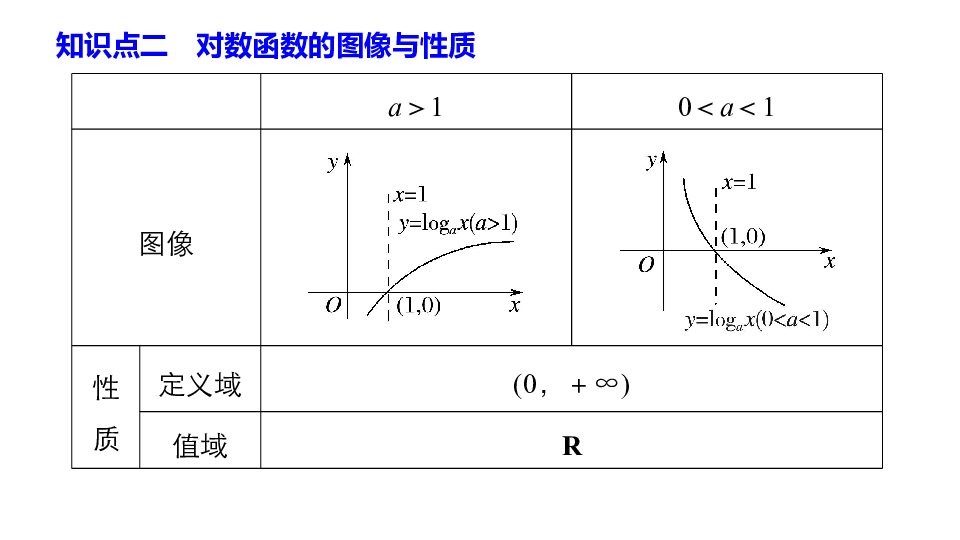
(3)在解析式y＝logax中，logax的系数必须为1，真数必须是x.答案y＝logax(a＞0，a≠1)x(0，＋∞)知识点二　对数函数的图像与性质答案(1,0)y＜0y＞0y＞0y＜0增函数减函数知识点三　反函数
对数函数y＝logax(a＞0，a≠1)与 互为反函数.答案指数函数y＝ax(a＞0，a≠1)返回 题型探究 重点突破题型一　对数函数的概念
例1　指出下列函数哪些是对数函数？
(1)y＝3log2x；解析答案解　log2x的系数是3，不是1，不是对数函数.(2)y＝log6x；解　符合对数函数的结构形式，是对数函数.(3)y＝logx3；解　自变量在底数位置上，不是对数函数.(4)y＝log2x＋1.解　对数式log2x后又加1，不是对数函数.反思与感悟判断一个函数是对数函数必须是形如y＝logax(a＞0，a≠1)的形式，即必须满足以下条件：
(1)系数为1.
(2)底数为大于0且不等于1的常数.
(3)对数的真数仅有自变量x.答案D跟踪训练1　下列函数为对数函数的是(　　)
A.y＝log1x B.y＝3log2x
C.y＝log2(x＋1) D.y＝log2x解析答案反思与感悟反思与感悟答案　A对数函数图像特点：
(1)底数大于1，图像呈上升趋势；底数大于0小于1，图像呈下降趋势.
(2)在第一象限，各图像对应的对数函数底数顺时针增大.底数越小，在第一象限图像越靠近y轴；底数越大，在第一象限图像越靠近x轴.跟踪训练2　如图，若C1，C2分别为函数y＝logax和y＝logbx的图像，则(　　)解析答案A.0C.a>b>1 D.b>a>1
解析　两图像均呈下降趋势，所以a，b均小于1.结合第一象限图像特征得bA.(1,2) B.(2,1)
C.(－2,1) D.(－1,1)解析答案解析　令x＋2＝1，即x＝－1，得y＝loga1＋1＝1，故函数y＝loga(x＋2)＋1的图像过定点(－1,1).D反思与感悟求解对数型函数过定点问题，一般先令真数等于1，求出横坐标x，再求出纵坐标值y，即可得定点坐标.跟踪训练3　函数f(x)＝loga(2x＋1)＋2(a>0，a≠1)的图像必过定点的坐标为________.解析答案解析　当x＝0时，f(x)＝2，所以函数f(x)的图像必过定点(0,2).(0,2)解析答案C解析答案C反思与感悟求与对数函数有关的函数定义域时，除遵循前面已学习过的求函数定义域的方法外，还要对这种函数自身有如下要求：一是要特别注意真数大于零；二是要注意对数的底数；三是按底数的取值应用单调性，有针对性地解不等式.解析答案解得x＞2且x≠3.
∴函数的定义域为(2,3)∪(3，＋∞).(2)f(x)＝log(x＋1)(16－4x).解析答案解得－1＜x＜0或0＜x＜4.
∴函数的定义域为(－1,0)∪(0,4).解析答案∴它的反函数为对数函数解析答案(2)y＝log7x的反函数为________.
解析　∵对数函数y＝log7x的底数为7.
∴它的反函数为指数函数y＝7x.
(3)点(4,16)在函数y＝logax(a>0，a≠1)的反函数的图像上，则a＝________.
解析　∵函数y＝logax(a>0，a≠1)的反函数是y＝ax(a>0，a≠1)，
又∵点(4,16)在函数y＝ax(a>0，a≠1)的图像上.
∴16＝a4，∴a＝2.y＝7x2反思与感悟1.同底的对数函数与指数函数互为反函数.
2.互为反函数的两个函数图像关于直线y＝x对称.解析答案C求解对数函数定义域考虑不全致误易错点解析答案例6　求函数y＝log(x＋1)(16－4x)的定义域.错解　由16－4x>0，解得x<2，
∴函数定义域为(－∞，2).∴函数的定义域为(－1,0)∪(0,2).
纠错心得　求对数函数的定义域，要满足：(1)真数大于零；(2)底数大于零且不等于1.注意要同时满足这两个条件，不能漏掉其中一个.解析答案跟踪训练6　求函数f(x)＝log(2x－4)(10－2x)的定义域.返回 当堂检测12345解析答案1.下列函数是对数函数的是(　　)
A.y＝loga(2x) B.y＝log22x
C.y＝log2x＋1 D.y＝lg x
解析　选项A、B、C中的函数都不具有“y＝logax(a＞0，a≠1)”的形式，只有D选项符合.D12345解析答案D123453.函数y＝ax与y＝－logax(a＞0，a≠1)在同一坐标系中的图像形状可能是(　　)解析答案12345解析　函数y＝－logax恒过定点(1,0)，排除B项；
当a＞1时，y＝ax是增函数，y＝－logax是减函数，当0答案　A12345解析答案4.若a＞0，a≠1，则函数y＝loga(x－1)＋1的图像恒过定点________.解析　函数图像过定点，则与a无关，故loga(x－1)＝0，
∴x－1＝1，x＝2，y＝1，所以y＝loga(x－1)＋1过定点(2,1).(2,1)12345解析答案解析　∵f(x)的反函数图像过(4,2)，
∴f(x)的图像过(2,4)，∴a2－1＝4，∴a＝4.5.若函数f(x)＝ax－1的反函数的图像过点(4,2)，则a＝________.4课堂小结1.判断一个函数是不是对数函数，关键是分析所给函数是否具有y＝logax(a＞0，a≠1)这种形式.
2.在对数函数y＝logax中，底数a对其图像直接产生影响，学会以分类的观点认识和掌握对数函数的图像和性质.
3.涉及对数函数定义域的问题，常从真数和底数两个角度分析.返回