2017年如东县八年级下《第11章反比例函数》测试题含答案
文档属性
| 名称 | 2017年如东县八年级下《第11章反比例函数》测试题含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 303.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-18 20:31:01 | ||
图片预览

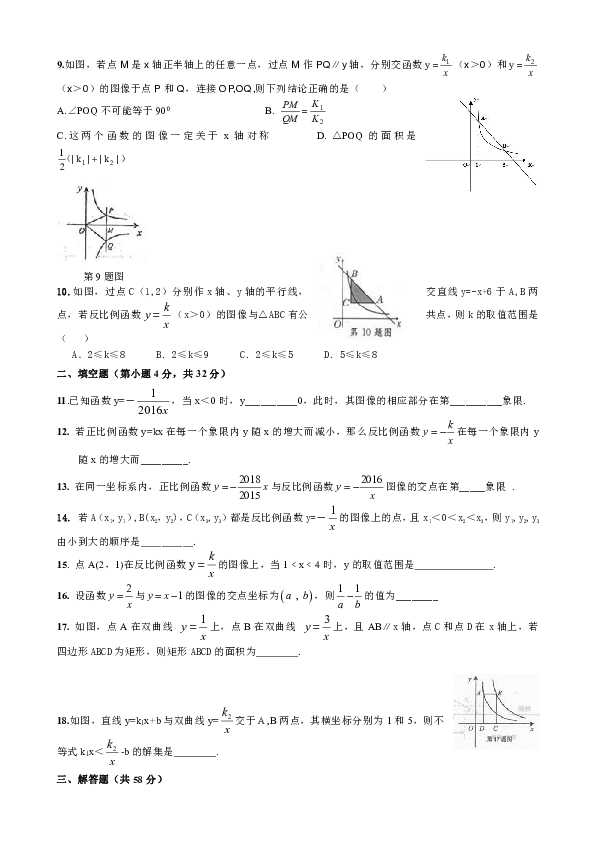
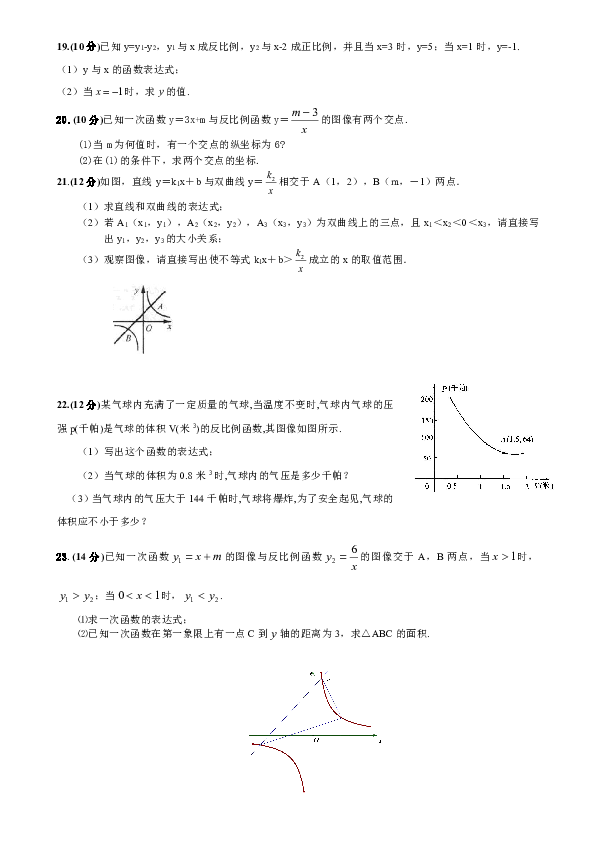
文档简介
2016-2017年度数学八年级下第11章反比例函数
单元测试题
(时间:90分钟
满分:120分)
(班级:
姓名:
得分:
)
一、选择题(第小题3分,共30分)
1.
观察下列函数:,,,.其中反比例函数有(
)
A.
1个
B.
2个
C.
3个
D.
4个
2.
反比例函数,,的共同特点是(
)
A.
图像位于相同的象限内
B.
自变量的取值范围是全体实数
C.
在第一象限内y随x的增大而减小
D.
图像都不与坐标轴相交
3.
在反比例函数图像的每一支曲线上,y都随x的增大而增大,则k的值可以是(
)
A
.2016
B.0
C.2015
D.
4.
已知函数是反比例函数,且图像在第二、四象限内,则m的值是(
)
A.3
B. C.
D.
5.如图,正比例函数y1=k1x和反比例函数y2=的图像交于A(-1,2),
B(1,-2)两点,若y1
<y2,则x的取值范围是(
)
A.x<-1或x>1
B.
x<-1或0<x<1
C.
-1<x<0或
0<x<1
D.
-1<x<0或x>1
6.如果反比例函数的图像经过点A(-1,-2),则当>1时,函数值y的取值范围是(
)
A.y>1
B.
0<
y<2
C.
y>2
D.0<y<1
7.
反比例函数图像上的两点为(x1,y1),(x2,y2),且x1)
A.y1>y2
B.y1C.y1=y2
D.不能确定
8.当a≠0时,函数y=ax+1与函数y=在同一坐标系中的图像可能是( )
9.如图,若点M是x轴正半轴上的任意一点,过点M作PQ∥y轴,分别交函数(x>0)和(x>0)的图像于点P和Q,连接OP,OQ,则下列结论正确的是(
)
A.∠POQ不可能等于900
B.
C.这两个函数的图像一定关于x轴对称
D.
△POQ的面积是
第9题图
10.如图,过点C(1,2)分别作x轴、y轴的平行线,交直线y=-x+6于A,B两点,若反比例函数(x>0)的图像与△ABC有公共点,则k的取值范围是(
)
A.2≤k≤8
B.
2≤k≤9
C.
2≤k≤5
D.
5≤k≤8
二、填空题(第小题4分,共32分)
11.已知函数y=-,当x<0时,y__________0,此时,其图像的相应部分在第__________象限.
12.
若正比例函数y=kx在每一个象限内y随x的增大而减小,那么反比例函数在每一个象限内y随x的增大而_________.
13.
在同一坐标系内,正比例函数与反比例函数图像的交点在第_____象限
.
14.
若A(x1,y1),B(x2,y2),C(x3,y3)都是反比例函数y=-的图像上的点,且x1<0<x2<x3,则y1,y2,y3由小到大的顺序是__________.
15.
点A(2,1)在反比例函数的图像上,当1﹤x﹤4时,y的取值范围是
.
16.
设函数与的图像的交点坐标为,则的值为________
17.
如图,点A在双曲线
上,点B在双曲线
上,且AB∥x轴,点C和点D在x轴上,若四边形ABCD为矩形,则矩形ABCD的面积为
.
18.如图,直线y=k1x+b与双曲线y=交于A,B两点,其横坐标分别为1和5,则不等式k1x<-b的解集是
.
三、解答题(共58分)
19.(10分)已知y=y1-y2,y1与x成反比例,y2与x-2成正比例,并且当x=3时,y=5;当x=1时,y=-1.
(1)y与x的函数表达式;
(2)当时,求的值.
20.(10分)已知一次函数y=3x+m与反比例函数y=的图像有两个交点.
(1)当m为何值时,有一个交点的纵坐标为6
(2)在(1)的条件下,求两个交点的坐标.
21.(12分)如图,直线y=k1x+b与双曲线y=相交于A(1,2),B(m,-1)两点.
(1)求直线和双曲线的表达式;
(2)若A1(x1,y1),A2(x2,y2),A3(x3,y3)为双曲线上的三点,且x1<x2<0<x3,请直接写出y1,y2,y3的大小关系;
(3)观察图像,请直接写出使不等式k1x+b>成立的x的取值范围.
22.(12分)某气球内充满了一定质量的气球,当温度不变时,气球内气球的压强p(千帕)是气球的体积V(米3)的反比例函数,其图像如图所示.
(1)写出这个函数的表达式;
(2)当气球的体积为0.8米3时,气球内的气压是多少千帕?
(3)当气球内的气压大于144千帕时,气球将爆炸,为了安全起见,气球的体积应不小于多少?
23.(14分)已知一次函数的图像与反比例函数的图像交于A,B两点,当时,;当时,.
⑴求一次函数的表达式;
⑵已知一次函数在第一象限上有一点C到轴的距离为3,求△ABC的面积.
参考答案
一、1.B
2.
D
3.
A
4.
B
5.
D
6.
B
7.
D
8.
C
9.
D
10.
B
二、11.>
二
12.
.减小
13.
二、四
14.
.y2<y3<y1
15.
16.
17.
2
18.0<x<1或x>5
三、19.解:(1)设,则y=-k2(x-2).
由题意,得解得所以y与x的函数表达式为y=+4(x-2).
(2)当时,.
20.解:(1)把y=6分别代入y=3x+m和y=,
得
3x+m=6,
=6.
解得m=5.
(2)由(1)得一次函数为y=3x+5,反比例函数为y=.
解得
∴两个函数图像的交点为(-2,-1)和(,6).
21.解:(1)∵双曲线y=经过点A(1,2),∴k2=2.∴双曲线的表达式为y=.
∵点B(m,-1)在双曲线y=上,∴m=-2,则B(-2,-1).
由点A(1,2),B(-2,-1)在直线y=k1x+b上,得
解得∴直线的表达式为y=x+1.
(2)y2<y1<y3.
(3)x>1或-2<x<0.
22.
(1)
(2)当米3时,20千帕
(3)∵,∴.为了安全起见,气球的体积应不小于米3.
23.解:(1)根据题意知,点A的坐标为(1,6),代人y1=x+m,
得m=5.∴
一次函数的表达式为y1=x+5.
(2)如图,过点B作直线BD平行于x轴,交AC的延长线于D.
∵点C到y轴的距离为3,∴C点的横坐标为3.
又C在双曲线上,∴y=,即C(3,2).
解得,∴B(-6,-1).
设AC的表达式为y=k1x+b1,把点A(1,6),点C(3,2)代入,得解得k1=-2,b1=8.∴直线AC的表达式为y=-2x+8.
当y=-1时-1=-2x+8,
x=4.5,即点D(4.5,-1)
∴==21.
单元测试题
(时间:90分钟
满分:120分)
(班级:
姓名:
得分:
)
一、选择题(第小题3分,共30分)
1.
观察下列函数:,,,.其中反比例函数有(
)
A.
1个
B.
2个
C.
3个
D.
4个
2.
反比例函数,,的共同特点是(
)
A.
图像位于相同的象限内
B.
自变量的取值范围是全体实数
C.
在第一象限内y随x的增大而减小
D.
图像都不与坐标轴相交
3.
在反比例函数图像的每一支曲线上,y都随x的增大而增大,则k的值可以是(
)
A
.2016
B.0
C.2015
D.
4.
已知函数是反比例函数,且图像在第二、四象限内,则m的值是(
)
A.3
B. C.
D.
5.如图,正比例函数y1=k1x和反比例函数y2=的图像交于A(-1,2),
B(1,-2)两点,若y1
<y2,则x的取值范围是(
)
A.x<-1或x>1
B.
x<-1或0<x<1
C.
-1<x<0或
0<x<1
D.
-1<x<0或x>1
6.如果反比例函数的图像经过点A(-1,-2),则当>1时,函数值y的取值范围是(
)
A.y>1
B.
0<
y<2
C.
y>2
D.0<y<1
7.
反比例函数图像上的两点为(x1,y1),(x2,y2),且x1
A.y1>y2
B.y1
D.不能确定
8.当a≠0时,函数y=ax+1与函数y=在同一坐标系中的图像可能是( )
9.如图,若点M是x轴正半轴上的任意一点,过点M作PQ∥y轴,分别交函数(x>0)和(x>0)的图像于点P和Q,连接OP,OQ,则下列结论正确的是(
)
A.∠POQ不可能等于900
B.
C.这两个函数的图像一定关于x轴对称
D.
△POQ的面积是
第9题图
10.如图,过点C(1,2)分别作x轴、y轴的平行线,交直线y=-x+6于A,B两点,若反比例函数(x>0)的图像与△ABC有公共点,则k的取值范围是(
)
A.2≤k≤8
B.
2≤k≤9
C.
2≤k≤5
D.
5≤k≤8
二、填空题(第小题4分,共32分)
11.已知函数y=-,当x<0时,y__________0,此时,其图像的相应部分在第__________象限.
12.
若正比例函数y=kx在每一个象限内y随x的增大而减小,那么反比例函数在每一个象限内y随x的增大而_________.
13.
在同一坐标系内,正比例函数与反比例函数图像的交点在第_____象限
.
14.
若A(x1,y1),B(x2,y2),C(x3,y3)都是反比例函数y=-的图像上的点,且x1<0<x2<x3,则y1,y2,y3由小到大的顺序是__________.
15.
点A(2,1)在反比例函数的图像上,当1﹤x﹤4时,y的取值范围是
.
16.
设函数与的图像的交点坐标为,则的值为________
17.
如图,点A在双曲线
上,点B在双曲线
上,且AB∥x轴,点C和点D在x轴上,若四边形ABCD为矩形,则矩形ABCD的面积为
.
18.如图,直线y=k1x+b与双曲线y=交于A,B两点,其横坐标分别为1和5,则不等式k1x<-b的解集是
.
三、解答题(共58分)
19.(10分)已知y=y1-y2,y1与x成反比例,y2与x-2成正比例,并且当x=3时,y=5;当x=1时,y=-1.
(1)y与x的函数表达式;
(2)当时,求的值.
20.(10分)已知一次函数y=3x+m与反比例函数y=的图像有两个交点.
(1)当m为何值时,有一个交点的纵坐标为6
(2)在(1)的条件下,求两个交点的坐标.
21.(12分)如图,直线y=k1x+b与双曲线y=相交于A(1,2),B(m,-1)两点.
(1)求直线和双曲线的表达式;
(2)若A1(x1,y1),A2(x2,y2),A3(x3,y3)为双曲线上的三点,且x1<x2<0<x3,请直接写出y1,y2,y3的大小关系;
(3)观察图像,请直接写出使不等式k1x+b>成立的x的取值范围.
22.(12分)某气球内充满了一定质量的气球,当温度不变时,气球内气球的压强p(千帕)是气球的体积V(米3)的反比例函数,其图像如图所示.
(1)写出这个函数的表达式;
(2)当气球的体积为0.8米3时,气球内的气压是多少千帕?
(3)当气球内的气压大于144千帕时,气球将爆炸,为了安全起见,气球的体积应不小于多少?
23.(14分)已知一次函数的图像与反比例函数的图像交于A,B两点,当时,;当时,.
⑴求一次函数的表达式;
⑵已知一次函数在第一象限上有一点C到轴的距离为3,求△ABC的面积.
参考答案
一、1.B
2.
D
3.
A
4.
B
5.
D
6.
B
7.
D
8.
C
9.
D
10.
B
二、11.>
二
12.
.减小
13.
二、四
14.
.y2<y3<y1
15.
16.
17.
2
18.0<x<1或x>5
三、19.解:(1)设,则y=-k2(x-2).
由题意,得解得所以y与x的函数表达式为y=+4(x-2).
(2)当时,.
20.解:(1)把y=6分别代入y=3x+m和y=,
得
3x+m=6,
=6.
解得m=5.
(2)由(1)得一次函数为y=3x+5,反比例函数为y=.
解得
∴两个函数图像的交点为(-2,-1)和(,6).
21.解:(1)∵双曲线y=经过点A(1,2),∴k2=2.∴双曲线的表达式为y=.
∵点B(m,-1)在双曲线y=上,∴m=-2,则B(-2,-1).
由点A(1,2),B(-2,-1)在直线y=k1x+b上,得
解得∴直线的表达式为y=x+1.
(2)y2<y1<y3.
(3)x>1或-2<x<0.
22.
(1)
(2)当米3时,20千帕
(3)∵,∴.为了安全起见,气球的体积应不小于米3.
23.解:(1)根据题意知,点A的坐标为(1,6),代人y1=x+m,
得m=5.∴
一次函数的表达式为y1=x+5.
(2)如图,过点B作直线BD平行于x轴,交AC的延长线于D.
∵点C到y轴的距离为3,∴C点的横坐标为3.
又C在双曲线上,∴y=,即C(3,2).
解得,∴B(-6,-1).
设AC的表达式为y=k1x+b1,把点A(1,6),点C(3,2)代入,得解得k1=-2,b1=8.∴直线AC的表达式为y=-2x+8.
当y=-1时-1=-2x+8,
x=4.5,即点D(4.5,-1)
∴==21.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
