1.4整式的乘法同步练习（解析版）

1.4整式的乘法
同步练习
一、单选题
1、若（x+2）（x﹣1）=x2+mx+n，则m+n=（?? ）
A、1B、﹣2C、﹣1D、2
2、下列计算正确的是（?? ）
A、x?2x=2xB、x3?x2=x5C、（x2）3=x5D、（2x）2=2x2
3、单项式乘以多项式运算法则的依据是（?? ）
A、乘法交换律B、加法结合律C、乘法分配律D、加法交换律
4、如（x+a）与（x+3）的乘积中不含x的一次项，则a的值为（?? ）
A、3B、﹣3C、1D、﹣1
5、李老师做了个长方形教具，其中一边长为2a+b，另一边长为a﹣b，则该长方形的面积为（?? ） 21·世纪*教育网
A、6a+bB、2a2﹣ab﹣b2C、3aD、10a﹣b
6、若将代数式中的任意两个字母交换，代数式不变，则称这个代数式为完全对称式，如a+b+c就是完全对称式．下列三个代数式： ①（a﹣b）2；②（2a﹣b）（2a+b）；③a（a+b）．其中是完全对称式的是（?? ） www-2-1-cnjy-com
A、③B、①③C、②③D、①
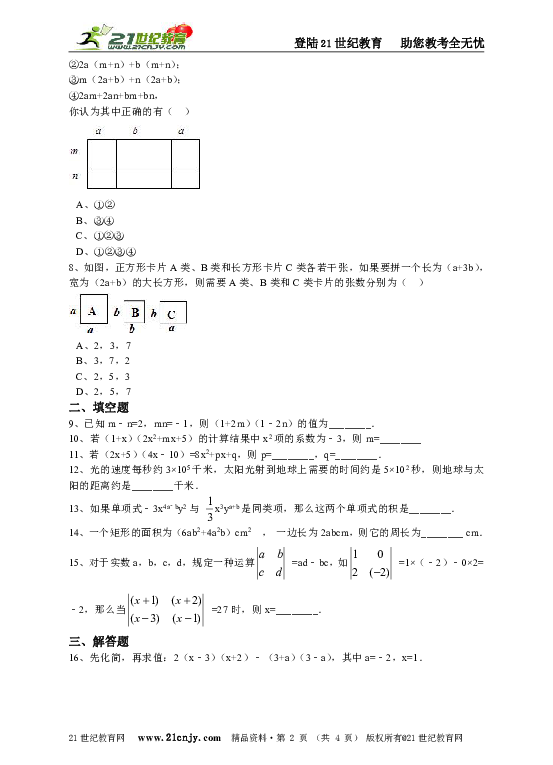
7、如图，甲、乙、丙、丁四位同学给出了四种表示该长方形面积的多项式： ①（2a+b）（m+n）；②2a（m+n）+b（m+n）；③m（2a+b）+n（2a+b）；④2am+2an+bm+bn，你认为其中正确的有（?? ）2-1-c-n-j-y
A、①②B、③④C、①②③D、①②③④
8、如图，正方形卡片A类、B类和长方形卡片C类各若干张，如果要拼一个长为（a+3b），宽为（2a+b）的大长方形，则需要A类、B类和C类卡片的张数分别为（?? ） 21*cnjy*com
A、2，3，7B、3，7，2C、2，5，3D、2，5，7
二、填空题
9、已知m﹣n=2，mn=﹣1，则（1+2m）（1﹣2n）的值为________．
10、若（1+x）（2x2+mx+5）的计算结果中x2项的系数为﹣3，则m=________
11、若（2x+5）（4x﹣10）=8x2+px+q，则p=________，q=________．
12、光的速度每秒约3×105千米，太阳光射到地球上需要的时间约是5×102秒，则地球与太阳的距离约是________千米． 【来源：21·世纪·教育·网】
13、如果单项式﹣3x4a﹣by2与 x3ya+b是同类项，那么这两个单项式的积是________．
14、一个矩形的面积为（6ab2+4a2b）cm2 ， 一边长为2abcm，则它的周长为________?cm．
15、对于实数a，b，c，d，规定一种运算 =ad﹣bc，如 =1×（﹣2）﹣0×2=﹣2，那么当 =27时，则x=________． 【来源：21cnj*y.co*m】
三、解答题
16、先化简，再求值：2（x﹣3）（x+2）﹣（3+a）（3﹣a），其中a=﹣2，x=1．

17、已知一个多项式除以a2﹣3a+1得到商式是2a+1，求这个多项式．

若3x2﹣2x+b与x2+bx﹣1的和中不存在含x的项，试求b的值，写出它们的和，并证明不论x取什么值，它的值总是正数．21cnjy.com

甲、乙两人共同计算一道整式乘法：（2x+a）（3x+b），由于甲抄错了第一个多项式中a前面的符号，得到的结果为6x2+18x+12；由于乙漏抄了第二个多项中的x的系数，得到的结果为2x2+2x﹣12，请你计算出a、b的值各是多少，并写出这道整式乘法的正确结果．

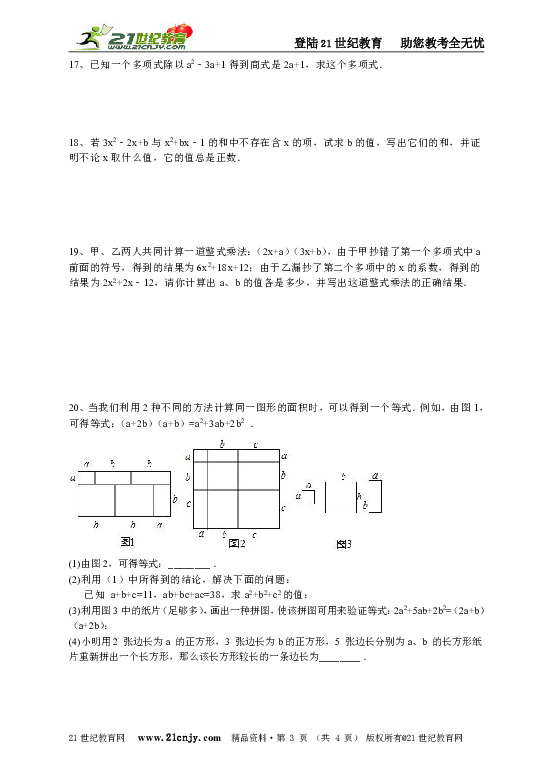
20、当我们利用2种不同的方法计算同一图形的面积时，可以得到一个等式．例如，由图1，可得等式：（a+2b）（a+b）=a2+3ab+2b2 ．
(1)由图2，可得等式：________?．
(2)利用（1）中所得到的结论，解决下面的问题：???? 已知 a+b+c=11，ab+bc+ac=38，求a2+b2+c2的值； 21教育网
(3)利用图3中的纸片（足够多），画出一种拼图，使该拼图可用来验证等式：2a2+5ab+2b2=（2a+b）（a+2b）； 21·cn·jy·com
(4)小明用2 张边长为a 的正方形，3 张边长为b的正方形，5 张边长分别为a、b 的长方形纸片重新拼出一个长方形，那么该长方形较长的一条边长为________?．
答案解析
单选题
题号
1
2
3
4
5
6
7
8
答案
C
B
C
B
B
D
D
A
解析：
3、C 解：乘法的分配律：a（b+c）=ab+ac． 故选C．4、B 解：原式=x2+（a+3）x+3a， 由结果不含x的一次项，得到a+3=0，解得：a=﹣3，故选B5、B 解：根据题意得：（2a+b）（a﹣b）=2a2﹣2ab+ab﹣b2=2a2﹣ab﹣b2 ． 故选B．6、D 解：①（a﹣b）2=（b﹣a）2 ， 是完全对称式， ②（2a﹣b）（2a+b）≠（2b﹣a）（2b+a），不是完全对称式；③a（a+b）≠b（b+a），不是完全对称式．故选D．7、D 解：①（2a+b）（m+n），本选项正确；②长方形的面积等于左边，中间及右边的长方形面积之和，表示即可；③长方形的面积等于上下两个长方形面积之和，表示即可；④长方形的面积由6个长方形的面积之和，表示即可．②2a（m+n）+b（m+n），本选项正确；③m（2a+b）+n（2a+b），本选项正确；④2am+2an+bm+bn，本选项正确，则正确的有①②③④．故选D． 21世纪教育网版权所有
8、A 解：长为a+3b，宽为2a+b的长方形的面积为： （a+3b）（2a+b）=2a2+7ab+3b2 ， ∵A类卡片的面积为a2 ， B类卡片的面积为b2 ， C类卡片的面积为ab，∴需要A类卡片2张，B类卡片3张，C类卡片7张．故选：A． www.21-cn-jy.com
二、填空题
9、9 解：∵m﹣n=2，mn=﹣1， ∴（1+2m）（1﹣2n）=1﹣2n+2m﹣4mn=1+2（m﹣n）﹣4mn=1+4+4=9．故答案为：9．10、-5 解：∵（1+x）（2x2+mx+5）=2x3+（2+m）x2+（5+m）x+5， 又∵结果中x2项的系数为﹣3，∴2+m=﹣3，解得m=﹣5．11、0；﹣50 解：已知等式整理得：8x2﹣50=8x2+px+q， 则p=0，q=﹣50，故答案为：0，﹣5012、1.5×108 解：3×105×5×102=15×107=1.5×108千米．故答案为：1.5×108 ． 13、﹣x6y4 解：由同类项的定义，得 ，解得： ∴原单项式为：﹣3x3y2和 x3y2 ， 其积是﹣x6y4 ． 故答案为：﹣x6y414、4ab+4a+6b 解：（6ab2+4a2b）÷2ab=3b+2a， 2×（2ab+3b+2a）=4ab+4a+6b．故答案为：4ab+4a+6b．15、22 解：∵ =27， ∴（x+1）（x﹣1）﹣（x+2）（x﹣3）=27，∴x2﹣1﹣（x2﹣x﹣6）=27，∴x2﹣1﹣x2+x+6=27，∴x=22；故答案为：22． 2·1·c·n·j·y
三、解答题
16、解：原式=2（x2﹣x﹣6）﹣（9﹣a2）=2x2﹣2x+a2﹣21，当a=﹣2，x=1时，原式=2×12﹣2×1+（﹣2）2﹣21=﹣17 17、解：根据题意得：（a2﹣3a+1）（2a+1）=2a3+a2﹣6a2﹣3a+2a+1=2a3﹣5a2﹣a+1．则这个多项式是2a3﹣5a2﹣a+1． 18、解：由3x2﹣2x+b与x2+bx﹣1的和中不存在含x的项，得 （3x2﹣2x+b）+（x2+bx﹣1）=4x2+（b﹣2）x+（b﹣1），得b﹣2=0，解得b=2；3x2﹣2x+b与x2+bx﹣1的和是4x2+1，由平方都是非负数，得4x2+1≥1，不论x取什么值，它的值总是正数 19、解：由题意得（2x﹣a）（3x+b）=6x2+（2b﹣3a）x﹣ab=6x2+18x+12，∴2b﹣3a=18①；（2x+a）（x+b）=2x2+（2b+a）x+ab=2x2+2x﹣12，∴2b+a=2②，②﹣①得：4a=﹣16，即a=﹣4，把a=﹣4代入②得：b=3，则正确过程为（2x﹣4）（3x+3）=6x2﹣6x﹣12．