九年级数学下第26章二次函数测试题含答案
文档属性
| 名称 | 九年级数学下第26章二次函数测试题含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 378.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-19 13:14:32 | ||
图片预览


文档简介
二次函数
测试题
一、选择题(每小题3分,共30分)
1.
下列函数不属于二次函数的是
(
)
A.y=(x-1)(x+2)
B.y=(x+1)2
C.
y=1-x2
D.
y=2(x+3)2-2x2
2.给出下列四个函数:,,(>0),其中随的增大而减小的函数有
(
)
.3个
.2个
.1个
.0个
3.
把二次函数化为的形式是
(
)
.
.
.
.
4.
下列说法错误的是
(
)
A.二次函数y=3x2中,当x>0时,y随x的增大而增大
B.二次函数y=-6x2中,当x=0时,y有最大值0
C.a越大图象开口越小,a越小图象开口越大
D.不论a是正数还是负数,抛物线y=ax2(a≠0)的顶点一定是坐标原点
5.二次函数,当y=8时,对应的的值是
(
)
A.3
B.5
C.-3或
5
D.3和-5
6.二次函数的对称轴是
(
)
A.
B.
C.
D.
7.如果将抛物线向下平移1个单位,那么所得新抛物线的解析式是
(
)
A.
B.
C.
D.
8.
若二次函数.当≤l时,随的增大而减小,则的取值范围是(
)
A.=l
B.>l
C.≥l
D.≤l
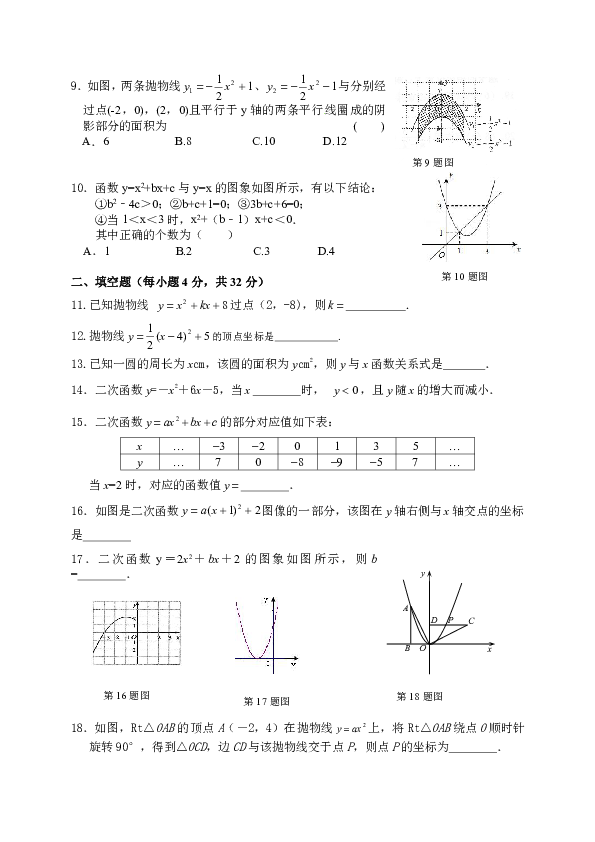
9.如图,两条抛物线、与分别经过点(-2,0),(2,0)且平行于y轴的两条平行线圈成的阴影部分的面积为
(
)
A.6
B.8
C.10
D.12
10.函数y=x2+bx+c与y=x的图象如图所示,有以下结论:
①b2﹣4c>0;②b+c+1=0;③3b+c+6=0;
④当1<x<3时,x2+(b﹣1)x+c<0.
其中正确的个数为( )
A.1
B.2
C.3
D.4
二、填空题(每小题4分,共32分)
11.已知抛物线
过点(2,-8),则
.
12.抛物线的顶点坐标是
.
13.已知一圆的周长为xcm,该圆的面积为ycm2,则y与x函数关系式是
.
14.二次函数y=-x2+6x-5,当
时,
,且随的增大而减小.
15.二次函数的部分对应值如下表:
x
…
…
y
…
…
当x=2时,对应的函数值
.
16.如图是二次函数图像的一部分,该图在轴右侧与轴交点的坐标是
17.二次函数y=2x2+bx+2的图象如图所示,则b
=
.
18.如图,Rt△OAB的顶点A(-2,4)在抛物线上,将Rt△OAB绕点O顺时针旋转90°,得到△OCD,边CD与该抛物线交于点P,则点P的坐标为
.
三、解答题(共58分)
19.(8分)函数(≠0)的图象与直线交于点(2,),求和的值.
20.(8分)已知函数。
(1)将它配成为的形式;
(2)写出此抛物线的开口方向、对称轴方程、顶点坐标;
21.(10分)某高中学校为高一新生设计的学生单人桌的抽屉部分是长方体形.其中,抽屉底面周长为180cm,高为20cm.请通过计算说明,当底面的宽x为何值时,抽屉的体积y最大?最大为多少?(材质及其厚度等暂忽略不计).
22.(10分)如图,矩形纸片ABCD中,AB=5,AD=4,四边形MNEF是在矩形纸片ABCD中裁剪出的一个正方形.你能否在该矩形中裁剪出一个面积最大的正方形?最大面积是多少?说明理由;
23.(12分)为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=﹣10x+500.
(1)李明在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?
(2)设李明获得的利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
(3)物价部门规定,这种节能灯的销售单价不得高于25元.如果李明想要每月获得的利润不低于300元,那么政府为他承担的总差价最少为多少元?
参考答案
一、1.
D
2.
A
3.
B
4.
C
5.
D
6.
C
7.
C
8.
C
9.
B
10.
B
二、11.-2,
12.(4,5)
13.
14.>5
15.0
16.(0,1)
17.4
18.,
三、19.解:由直线y=-x-2过点A(2,m),则m=-4.
由点A(2,-4)在抛物线y=ax2上,得a=-1
20.解:⑴
⑵开口向下,对称轴方程为,项点坐标为(-1,36)
21.解:已知抽屉底面宽为x
cm,则底面长为180÷2﹣x=(90﹣x)cm.
由题意得:y=x(90﹣x)×20
=﹣20(x2﹣90x)
=﹣20(x﹣45)2+40500
当x=45时,y有最大值,最大值为40500.
答:当抽屉底面宽为45cm时,抽屉的体积最大,最大体积为40500cm3.
22.解:(1)正方形的最大面积是16.
设AM=x(0≤x≤4)
,
则MD=4-x.
∵四边形MNEF是正方形,
∴MN=MF,∠AMN+∠FMD=90°.
∵∠AMN+∠ANM=90°,
∴∠ANM=∠FMD.
∴Rt△ANM≌Rt△DMF.
∴DM=AN.
∴
.
∵函数的开口向上,
对称轴是x=2,
函数图象如图所示,
∵0≤x≤4,
∴当x=0或x=4时,
正方形MNEF的面积最大.
最大值是16.
23.解:(1)当x=20时,y=﹣10x+500=﹣10×20+500=300,
300×(12﹣10)=300×2=600,
即政府这个月为他承担的总差价为600元.
(2)依题意得,w=(x﹣10)(﹣10x+500)
=﹣10x2+600x﹣5000
=﹣10(x﹣30)2+4000
∵a=﹣10<0,∴当x=30时,w有最大值4000.
即当销售单价定为30元时,每月可获得最大利润4000.
(3)由题意得:﹣10x2+600x﹣5000=3000,
解得:x1=20,x2=40.
∵a=﹣10<0,抛物线开口向下,
∴结合图象可知:当20≤x≤40时,w≥3000.
又∵x≤25,
∴当20≤x≤25时,w≥3000.
设政府每个月为他承担的总差价为p元,
∴p=(12﹣10)×(﹣10x+500)
=﹣20x+1000.
∵k=﹣20<0.
∴p随x的增大而减小,
∴当x=25时,p有最小值500.
即销售单价定为25元时,政府每个月为他承担的总差价最少为500元.
第9题图
第10题图
A
O
B
C
D
P
x
y
第17题图
第18题图
第16题图
A
B
C
D
M
N
E
F
x
y
O
2
16
测试题
一、选择题(每小题3分,共30分)
1.
下列函数不属于二次函数的是
(
)
A.y=(x-1)(x+2)
B.y=(x+1)2
C.
y=1-x2
D.
y=2(x+3)2-2x2
2.给出下列四个函数:,,(>0),其中随的增大而减小的函数有
(
)
.3个
.2个
.1个
.0个
3.
把二次函数化为的形式是
(
)
.
.
.
.
4.
下列说法错误的是
(
)
A.二次函数y=3x2中,当x>0时,y随x的增大而增大
B.二次函数y=-6x2中,当x=0时,y有最大值0
C.a越大图象开口越小,a越小图象开口越大
D.不论a是正数还是负数,抛物线y=ax2(a≠0)的顶点一定是坐标原点
5.二次函数,当y=8时,对应的的值是
(
)
A.3
B.5
C.-3或
5
D.3和-5
6.二次函数的对称轴是
(
)
A.
B.
C.
D.
7.如果将抛物线向下平移1个单位,那么所得新抛物线的解析式是
(
)
A.
B.
C.
D.
8.
若二次函数.当≤l时,随的增大而减小,则的取值范围是(
)
A.=l
B.>l
C.≥l
D.≤l
9.如图,两条抛物线、与分别经过点(-2,0),(2,0)且平行于y轴的两条平行线圈成的阴影部分的面积为
(
)
A.6
B.8
C.10
D.12
10.函数y=x2+bx+c与y=x的图象如图所示,有以下结论:
①b2﹣4c>0;②b+c+1=0;③3b+c+6=0;
④当1<x<3时,x2+(b﹣1)x+c<0.
其中正确的个数为( )
A.1
B.2
C.3
D.4
二、填空题(每小题4分,共32分)
11.已知抛物线
过点(2,-8),则
.
12.抛物线的顶点坐标是
.
13.已知一圆的周长为xcm,该圆的面积为ycm2,则y与x函数关系式是
.
14.二次函数y=-x2+6x-5,当
时,
,且随的增大而减小.
15.二次函数的部分对应值如下表:
x
…
…
y
…
…
当x=2时,对应的函数值
.
16.如图是二次函数图像的一部分,该图在轴右侧与轴交点的坐标是
17.二次函数y=2x2+bx+2的图象如图所示,则b
=
.
18.如图,Rt△OAB的顶点A(-2,4)在抛物线上,将Rt△OAB绕点O顺时针旋转90°,得到△OCD,边CD与该抛物线交于点P,则点P的坐标为
.
三、解答题(共58分)
19.(8分)函数(≠0)的图象与直线交于点(2,),求和的值.
20.(8分)已知函数。
(1)将它配成为的形式;
(2)写出此抛物线的开口方向、对称轴方程、顶点坐标;
21.(10分)某高中学校为高一新生设计的学生单人桌的抽屉部分是长方体形.其中,抽屉底面周长为180cm,高为20cm.请通过计算说明,当底面的宽x为何值时,抽屉的体积y最大?最大为多少?(材质及其厚度等暂忽略不计).
22.(10分)如图,矩形纸片ABCD中,AB=5,AD=4,四边形MNEF是在矩形纸片ABCD中裁剪出的一个正方形.你能否在该矩形中裁剪出一个面积最大的正方形?最大面积是多少?说明理由;
23.(12分)为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=﹣10x+500.
(1)李明在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?
(2)设李明获得的利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
(3)物价部门规定,这种节能灯的销售单价不得高于25元.如果李明想要每月获得的利润不低于300元,那么政府为他承担的总差价最少为多少元?
参考答案
一、1.
D
2.
A
3.
B
4.
C
5.
D
6.
C
7.
C
8.
C
9.
B
10.
B
二、11.-2,
12.(4,5)
13.
14.>5
15.0
16.(0,1)
17.4
18.,
三、19.解:由直线y=-x-2过点A(2,m),则m=-4.
由点A(2,-4)在抛物线y=ax2上,得a=-1
20.解:⑴
⑵开口向下,对称轴方程为,项点坐标为(-1,36)
21.解:已知抽屉底面宽为x
cm,则底面长为180÷2﹣x=(90﹣x)cm.
由题意得:y=x(90﹣x)×20
=﹣20(x2﹣90x)
=﹣20(x﹣45)2+40500
当x=45时,y有最大值,最大值为40500.
答:当抽屉底面宽为45cm时,抽屉的体积最大,最大体积为40500cm3.
22.解:(1)正方形的最大面积是16.
设AM=x(0≤x≤4)
,
则MD=4-x.
∵四边形MNEF是正方形,
∴MN=MF,∠AMN+∠FMD=90°.
∵∠AMN+∠ANM=90°,
∴∠ANM=∠FMD.
∴Rt△ANM≌Rt△DMF.
∴DM=AN.
∴
.
∵函数的开口向上,
对称轴是x=2,
函数图象如图所示,
∵0≤x≤4,
∴当x=0或x=4时,
正方形MNEF的面积最大.
最大值是16.
23.解:(1)当x=20时,y=﹣10x+500=﹣10×20+500=300,
300×(12﹣10)=300×2=600,
即政府这个月为他承担的总差价为600元.
(2)依题意得,w=(x﹣10)(﹣10x+500)
=﹣10x2+600x﹣5000
=﹣10(x﹣30)2+4000
∵a=﹣10<0,∴当x=30时,w有最大值4000.
即当销售单价定为30元时,每月可获得最大利润4000.
(3)由题意得:﹣10x2+600x﹣5000=3000,
解得:x1=20,x2=40.
∵a=﹣10<0,抛物线开口向下,
∴结合图象可知:当20≤x≤40时,w≥3000.
又∵x≤25,
∴当20≤x≤25时,w≥3000.
设政府每个月为他承担的总差价为p元,
∴p=(12﹣10)×(﹣10x+500)
=﹣20x+1000.
∵k=﹣20<0.
∴p随x的增大而减小,
∴当x=25时,p有最小值500.
即销售单价定为25元时,政府每个月为他承担的总差价最少为500元.
第9题图
第10题图
A
O
B
C
D
P
x
y
第17题图
第18题图
第16题图
A
B
C
D
M
N
E
F
x
y
O
2
16
