北师大版高中数学必修一第四章函数的应用 单元测试题
文档属性
| 名称 | 北师大版高中数学必修一第四章函数的应用 单元测试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 275.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-20 00:00:00 | ||
图片预览


文档简介
第四章函数的应用
单元测试题
学号:________
班级:________姓名:________得分:________
(时间:120分钟
满分:150分)
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个是符合题目要求的)
1.
下列函数中,随着x的增长,增长速度最快的是(
)
A.
y=50
B.
C.
D.
2.设,则在下列区间中使函数有零点的区间是
(
)
A.
B.
C.
D.
3.
a,b,c,d四个物体沿同一方向同时开始运动,假设其经过的路程和时间的函数关系分别是,如果运动的时间足够长,则运动在最前面的物体一定是
( )
A.a
B.b
C.c
D.d
4.
下表显示出函数值随自变量变化的一组数据,由此判断它最可能的函数模型是(
).
x
4
5
6
7
8
9
10
y
15
17
19
21
23
25
27
A.一次函数模型
B.二次函数模型
C.指数函数模型
D.对数函数模型
5.某单位为鼓励职工节约用水,作出如下规定:每位职工每月用水不超过10立方米的,按每立方米m元收费;用水超过10立方米的,超过部分按每立方米2m元收费.某职工某月缴水费16m元,则该职工这个月实际用水为( )立方米.
A.
13
B.
14
C.
18
D.
26
6.
某公司在甲、乙两地销售一种品牌车,利润(单位:万元)分别为L1=5.06x-0.15x2和L2=2x,其中x为销售量(单位:辆).若该公司在这两地共销售15辆车,则能获得的最大利润为( )
A.45.606万元
B.45.6万元
C.45.56万元
D.45.51万元
7.
设函数,若,,则函数的零点的个数是(
)
A.0
B.1
C.2
D.3
8.已知e是自然对数的底数,函数e的零点为,函数
的零点为,则下列不等式中成立的是
( )
A.
B.
C.
D.
9.已知某食品厂生产100克饼干的总费用为1.80元,现该食品厂对饼干采用两种包装,其包装费及售价如下表所示:
型号
小包装
大包装
质量
100克
300克
包装费
0.5元
0.8元
售价
3.00元
8.40元
下列说法中:
①买小包装实惠;②买大包装实惠;
③卖3包小包装比卖1包大包装盈利多;④卖1包大包装比卖3包小包装盈利多.
所有正确的说法是( )
①④
B.①③
C.②③
D.②④
10.
已知函数(),若函数在上有两个零点,则的取值范围是
A.
B.
C.
D.
11.已知a是f(x)=的零点,若0<x0<a,则f(x0)的值满足( )
A.
f(x0)<0
B.
f(x0)=
C.
f(x0)>0
D.
f(x0)的符号不确定
12.已知函数f(x)=x2﹣(a+b)x+ab+2(a<b)的两个零点为α,β(α<β),则实数a,b,α,β的大小关系是( )
A.
a<α<β<b
B.
α<a<β<b
C.
a<α<b<β
D.
α<a<b<β
二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中的横线上)
13.
14.
若方程的解所在区间是则整数k的值是______.
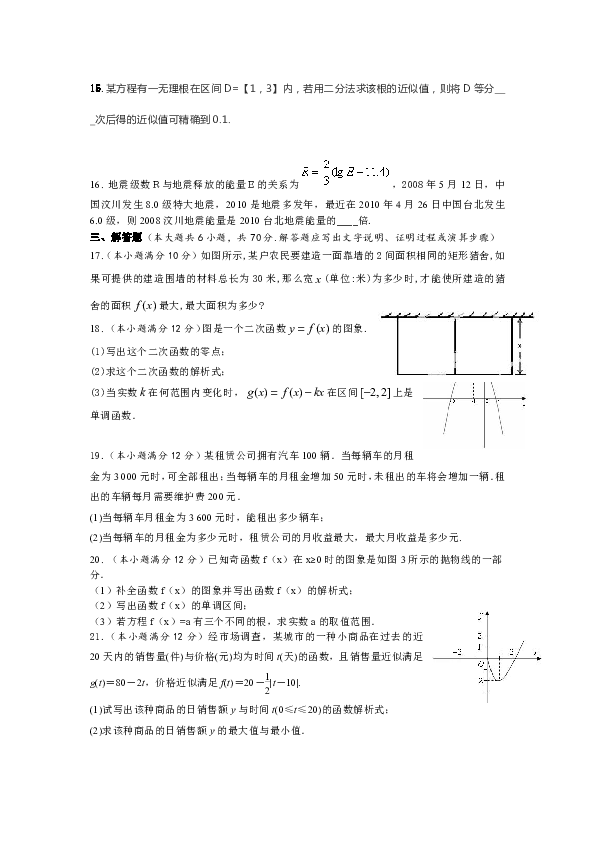
15.某方程有一无理根在区间D=【1,3】内,若用二分法求该根的近似值,则将D等分
次后得的近似值可精确到0.1.
16.
地震级数R与地震释放的能量E的关系为,2008年5月12日,中国汶川发生8.0级特大地震,2010是地震多发年,最近在2010年4月26日中国台北发生6.0级,则2008汶川地震能量是2010台北地震能量的____倍.
三、解答题(本大题共6小题,共70分.解答题应写出文字说明、证明过程或演算步骤)
17.(本小题满分10分)如图所示,某户农民要建造一面靠墙的2间面积相同的矩形猪舍,如果可提供的建造围墙的材料总长为30米,那么宽(单位:米)为多少时,才能使所建造的猪舍的面积最大,最大面积为多少
18.
(本小题满分12分)图是一个二次函数的图象.
(1)写出这个二次函数的零点;
(2)求这个二次函数的解析式;
(3)当实数在何范围内变化时,在区间上是单调函数.
19.(本小题满分12分)某租赁公司拥有汽车100辆.当每辆车的月租金为3
000元时,可全部租出;当每辆车的月租金增加50元时,未租出的车将会增加一辆.租出的车辆每月需要维护费200元.
(1)当每辆车月租金为3
600元时,能租出多少辆车;
(2)当每辆车的月租金为多少元时,租赁公司的月收益最大,最大月收益是多少元.
20.
(本小题满分12分)已知奇函数f(x)在x≥0时的图象是如图3所示的抛物线的一部分.
(1)补全函数f(x)的图象并写出函数f(x)的解析式;
(2)写出函数f(x)的单调区间;
(3)若方程f(x)=a有三个不同的根,求实数a的取值范围.
21.(本小题满分12分)经市场调查,某城市的一种小商品在过去的近20天内的销售量(件)与价格(元)均为时间t(天)的函数,且销售量近似满足g(t)=80-2t,价格近似满足f(t)=20-|t-10|.
(1)试写出该种商品的日销售额y与时间t(0≤t≤20)的函数解析式;
(2)求该种商品的日销售额y的最大值与最小值.
22.(本小题满分12分)已知函数.
(1)请在直角坐标系中画出函数f(x)的图象,并写出该函数的单调区间;
(2)若函数g(x)=f(x)﹣m恰有3个不同零点,求实数m的取值范围.
参考答案
一、选择题
1.
D
2.D
3.
D
4.
A
5.A
6.
B
7.C
8.A
9.D
10.
D
11.A
12.A
提示:
1.
根据函数的性质结合图象求解即可.
2.,由零点存在的条件知选D.
3.
根据四种函数的变化特点,指数函数是一个变化最快的函数,当运动的时间足够长,最前面的动物一定是按照指数函数运动的物体,即一定是第四种物体,故选D.
4.
随着自变量每增加1函数值增加2,函数值的增量是均匀的,故为线性函数即一次函数模型.故选A.
5.设该职工这个月实际用水为x立方米,因为每位职工每月用水不超过10立方米的,按每立方米m元水费收费,所以用水不超过10立方米的缴水费不超过10m元,因为该职工这个月缴水费16m元,所以该职工这个月实际用水超过10立方米,超过部分的水费=(x﹣10)×2m,所以由题意可列出一元一次方程式10m+(x﹣10)×2m=16m,解得x=13,故选A.
6.设在甲地销售x辆,则在乙地销售(15-x)辆,设总利润为L(x),则L(x)=L1+L2=5.06x-0.15x2+2(15-x)=-0.15x2+3.06x+30(0≤x≤15).L(x)在[0,10.2]上递增,在(10.2,+∞)上递减,所以当x=10时,L(x)最大,L(x)max=45.6(万元).故选B.
7.因为,,所以且,解得,即.即当时,由得,即,解得或.当时,由得,解得,不成立,舍去.所以函数的零点个数为2个,选C.
8.因为函数f(x)=e的零点为a,f(0)=-1<0,f(1)=e-1>0,所以0<a<1.因为函数g(x)=lnx+x-2的零点为b,g(1)=-1<0,g(2)=ln2>0,所以1<b<2.综上可得,0<a<1<b<2.再由函数f(x)=ex+x-2在(0,+∞)上是增函数,可得
f(a)<f(1)<f(b),故选A.
9.1包小包装每元买饼干克,1包大包装每元可买饼干>克,因此,买大包装实惠.卖3包小包装可盈利2.1元,卖1包大包装可盈利2.2元,因此,卖3包小包装比卖1包大包装盈利少.
10.
.当时,由得,.当时,由得.即,因为,所以,即,选D.
11.因为已知a是f(x)=的零点,所以f(a)=0.再由函数f(x)的解析式可得函数在区间(0,+∞)上是增函数,且
0<x0<a,可得f(x0)<0,故选A.
12.因为函数f(x)=x2﹣(a+b)x+ab+2=(x﹣a)(x﹣b)+2
的两个零点为α,β,设g(x)=x2﹣(a+b)x+ab=(x﹣a)(x﹣b),则a,b是函数g(x)的两个零点,则函数f(x)的图象可以看成把函数g(x)的图象向上平移2个单位得到的,如图1所示,故有a<α<β<b,故选A.
二、填空题
13.80
14.
15.
5
16.
1000
提示:
13.因为按照方案一缴费是:,又方案二比较少,所以,所以,即最大是80平米.
14.
构造函数,,画出函数的图象,两函数交点显然,当时,,所以k=-2.
15.因为每次被等分的两个区间长度一样,所以不妨设根始终在被等分的第一个区间,则它们是[1,2],[1,1.5],[1,1.25],[1,1.125],[1,1.0625],所以至少要等分5次.
16.
由已知条件得
解得,所以,同理:,解得,所以.
三、解答题
17.解:设长为,由题意知,可得即
,
当时,取得最大值75.
18.
解:(1)由图可知二次函数的零点为
(2)设二次函数为,点在函数上,解得.
所以.
(3),开口向下,对称轴为.
当,即时,在上递减;
当,
即时,在上递增
.
综上所述或.
19.解:(1)当每辆车的月租金定为3
600元时,未租出的车辆数为=12,所以这时租出88辆车.
(2)设每辆车的月租金定为x(x≥3
000)元,则租赁公司的月收益为
f(x)=(x-200),整理,得
f(x)=(8
000-x)(x-200)=-x2+164x-32
000=-(x-4
100)2+304
200.
故当x=4
100时,f(x)最大,最大值为f(4
100)=304
200,
即当每辆车的月租金定为4
100元时,租赁公司的月收益最大,最大月收益为304
200元.
20.
解:(1)根据奇函数的图象关于原点对称,故函数f(x)的图象如图2.
当x≥0时,设y=a(x﹣1)2﹣2,代入(2,0)得a=2,
即y=2=2x(x﹣1)2=2x2﹣4x.
同理求得当x<0时,设y=﹣2x2﹣4x.
所以.
由图可得函数f(x)的单调递增区间为(﹣∞,﹣1],[1,+∞),
函数f(x)的单调递减区间为[﹣1,1].
(3)由图可得y=f(x)与y=a有三个交点时,﹣2<a<2.
所以方程f(x)=a有三个不同的根,实数a的取值范围是(﹣2,2).
21.解:(1)y=g(t)·f(t)=(80-2t)·(20-|t-10|)=(40-t)(40-|t-10|)=
(2)当0≤t<10时,y的取值范围是[1
200,1
225],
在t=5时,y取得最大值为1
225;
当10≤t≤20时,y的取值范围是[600,1
200],
在t=20时,y取得最小值为600.
所以第5天,日销售额y取得最大值为1
225元;
第20天,日销售额y取得最小值为600元.
22.解:(1)f(x)=,函数f(x)的图象如图3所示.由图象得,函数f(x)的单调递减区间是(0,1),单调增区间是(﹣∞,0),(1,+∞).
(2)作出直线y=m,函数g(x)=f(x)﹣m恰有3个不同零点等价于函数y=m与函数f(x)的图象恰有三个不同公共点.
由函数f(x)=的图象易知.
故m的取值范围为(,1).
单元测试题
学号:________
班级:________姓名:________得分:________
(时间:120分钟
满分:150分)
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个是符合题目要求的)
1.
下列函数中,随着x的增长,增长速度最快的是(
)
A.
y=50
B.
C.
D.
2.设,则在下列区间中使函数有零点的区间是
(
)
A.
B.
C.
D.
3.
a,b,c,d四个物体沿同一方向同时开始运动,假设其经过的路程和时间的函数关系分别是,如果运动的时间足够长,则运动在最前面的物体一定是
( )
A.a
B.b
C.c
D.d
4.
下表显示出函数值随自变量变化的一组数据,由此判断它最可能的函数模型是(
).
x
4
5
6
7
8
9
10
y
15
17
19
21
23
25
27
A.一次函数模型
B.二次函数模型
C.指数函数模型
D.对数函数模型
5.某单位为鼓励职工节约用水,作出如下规定:每位职工每月用水不超过10立方米的,按每立方米m元收费;用水超过10立方米的,超过部分按每立方米2m元收费.某职工某月缴水费16m元,则该职工这个月实际用水为( )立方米.
A.
13
B.
14
C.
18
D.
26
6.
某公司在甲、乙两地销售一种品牌车,利润(单位:万元)分别为L1=5.06x-0.15x2和L2=2x,其中x为销售量(单位:辆).若该公司在这两地共销售15辆车,则能获得的最大利润为( )
A.45.606万元
B.45.6万元
C.45.56万元
D.45.51万元
7.
设函数,若,,则函数的零点的个数是(
)
A.0
B.1
C.2
D.3
8.已知e是自然对数的底数,函数e的零点为,函数
的零点为,则下列不等式中成立的是
( )
A.
B.
C.
D.
9.已知某食品厂生产100克饼干的总费用为1.80元,现该食品厂对饼干采用两种包装,其包装费及售价如下表所示:
型号
小包装
大包装
质量
100克
300克
包装费
0.5元
0.8元
售价
3.00元
8.40元
下列说法中:
①买小包装实惠;②买大包装实惠;
③卖3包小包装比卖1包大包装盈利多;④卖1包大包装比卖3包小包装盈利多.
所有正确的说法是( )
①④
B.①③
C.②③
D.②④
10.
已知函数(),若函数在上有两个零点,则的取值范围是
A.
B.
C.
D.
11.已知a是f(x)=的零点,若0<x0<a,则f(x0)的值满足( )
A.
f(x0)<0
B.
f(x0)=
C.
f(x0)>0
D.
f(x0)的符号不确定
12.已知函数f(x)=x2﹣(a+b)x+ab+2(a<b)的两个零点为α,β(α<β),则实数a,b,α,β的大小关系是( )
A.
a<α<β<b
B.
α<a<β<b
C.
a<α<b<β
D.
α<a<b<β
二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中的横线上)
13.
14.
若方程的解所在区间是则整数k的值是______.
15.某方程有一无理根在区间D=【1,3】内,若用二分法求该根的近似值,则将D等分
次后得的近似值可精确到0.1.
16.
地震级数R与地震释放的能量E的关系为,2008年5月12日,中国汶川发生8.0级特大地震,2010是地震多发年,最近在2010年4月26日中国台北发生6.0级,则2008汶川地震能量是2010台北地震能量的____倍.
三、解答题(本大题共6小题,共70分.解答题应写出文字说明、证明过程或演算步骤)
17.(本小题满分10分)如图所示,某户农民要建造一面靠墙的2间面积相同的矩形猪舍,如果可提供的建造围墙的材料总长为30米,那么宽(单位:米)为多少时,才能使所建造的猪舍的面积最大,最大面积为多少
18.
(本小题满分12分)图是一个二次函数的图象.
(1)写出这个二次函数的零点;
(2)求这个二次函数的解析式;
(3)当实数在何范围内变化时,在区间上是单调函数.
19.(本小题满分12分)某租赁公司拥有汽车100辆.当每辆车的月租金为3
000元时,可全部租出;当每辆车的月租金增加50元时,未租出的车将会增加一辆.租出的车辆每月需要维护费200元.
(1)当每辆车月租金为3
600元时,能租出多少辆车;
(2)当每辆车的月租金为多少元时,租赁公司的月收益最大,最大月收益是多少元.
20.
(本小题满分12分)已知奇函数f(x)在x≥0时的图象是如图3所示的抛物线的一部分.
(1)补全函数f(x)的图象并写出函数f(x)的解析式;
(2)写出函数f(x)的单调区间;
(3)若方程f(x)=a有三个不同的根,求实数a的取值范围.
21.(本小题满分12分)经市场调查,某城市的一种小商品在过去的近20天内的销售量(件)与价格(元)均为时间t(天)的函数,且销售量近似满足g(t)=80-2t,价格近似满足f(t)=20-|t-10|.
(1)试写出该种商品的日销售额y与时间t(0≤t≤20)的函数解析式;
(2)求该种商品的日销售额y的最大值与最小值.
22.(本小题满分12分)已知函数.
(1)请在直角坐标系中画出函数f(x)的图象,并写出该函数的单调区间;
(2)若函数g(x)=f(x)﹣m恰有3个不同零点,求实数m的取值范围.
参考答案
一、选择题
1.
D
2.D
3.
D
4.
A
5.A
6.
B
7.C
8.A
9.D
10.
D
11.A
12.A
提示:
1.
根据函数的性质结合图象求解即可.
2.,由零点存在的条件知选D.
3.
根据四种函数的变化特点,指数函数是一个变化最快的函数,当运动的时间足够长,最前面的动物一定是按照指数函数运动的物体,即一定是第四种物体,故选D.
4.
随着自变量每增加1函数值增加2,函数值的增量是均匀的,故为线性函数即一次函数模型.故选A.
5.设该职工这个月实际用水为x立方米,因为每位职工每月用水不超过10立方米的,按每立方米m元水费收费,所以用水不超过10立方米的缴水费不超过10m元,因为该职工这个月缴水费16m元,所以该职工这个月实际用水超过10立方米,超过部分的水费=(x﹣10)×2m,所以由题意可列出一元一次方程式10m+(x﹣10)×2m=16m,解得x=13,故选A.
6.设在甲地销售x辆,则在乙地销售(15-x)辆,设总利润为L(x),则L(x)=L1+L2=5.06x-0.15x2+2(15-x)=-0.15x2+3.06x+30(0≤x≤15).L(x)在[0,10.2]上递增,在(10.2,+∞)上递减,所以当x=10时,L(x)最大,L(x)max=45.6(万元).故选B.
7.因为,,所以且,解得,即.即当时,由得,即,解得或.当时,由得,解得,不成立,舍去.所以函数的零点个数为2个,选C.
8.因为函数f(x)=e的零点为a,f(0)=-1<0,f(1)=e-1>0,所以0<a<1.因为函数g(x)=lnx+x-2的零点为b,g(1)=-1<0,g(2)=ln2>0,所以1<b<2.综上可得,0<a<1<b<2.再由函数f(x)=ex+x-2在(0,+∞)上是增函数,可得
f(a)<f(1)<f(b),故选A.
9.1包小包装每元买饼干克,1包大包装每元可买饼干>克,因此,买大包装实惠.卖3包小包装可盈利2.1元,卖1包大包装可盈利2.2元,因此,卖3包小包装比卖1包大包装盈利少.
10.
.当时,由得,.当时,由得.即,因为,所以,即,选D.
11.因为已知a是f(x)=的零点,所以f(a)=0.再由函数f(x)的解析式可得函数在区间(0,+∞)上是增函数,且
0<x0<a,可得f(x0)<0,故选A.
12.因为函数f(x)=x2﹣(a+b)x+ab+2=(x﹣a)(x﹣b)+2
的两个零点为α,β,设g(x)=x2﹣(a+b)x+ab=(x﹣a)(x﹣b),则a,b是函数g(x)的两个零点,则函数f(x)的图象可以看成把函数g(x)的图象向上平移2个单位得到的,如图1所示,故有a<α<β<b,故选A.
二、填空题
13.80
14.
15.
5
16.
1000
提示:
13.因为按照方案一缴费是:,又方案二比较少,所以,所以,即最大是80平米.
14.
构造函数,,画出函数的图象,两函数交点显然,当时,,所以k=-2.
15.因为每次被等分的两个区间长度一样,所以不妨设根始终在被等分的第一个区间,则它们是[1,2],[1,1.5],[1,1.25],[1,1.125],[1,1.0625],所以至少要等分5次.
16.
由已知条件得
解得,所以,同理:,解得,所以.
三、解答题
17.解:设长为,由题意知,可得即
,
当时,取得最大值75.
18.
解:(1)由图可知二次函数的零点为
(2)设二次函数为,点在函数上,解得.
所以.
(3),开口向下,对称轴为.
当,即时,在上递减;
当,
即时,在上递增
.
综上所述或.
19.解:(1)当每辆车的月租金定为3
600元时,未租出的车辆数为=12,所以这时租出88辆车.
(2)设每辆车的月租金定为x(x≥3
000)元,则租赁公司的月收益为
f(x)=(x-200),整理,得
f(x)=(8
000-x)(x-200)=-x2+164x-32
000=-(x-4
100)2+304
200.
故当x=4
100时,f(x)最大,最大值为f(4
100)=304
200,
即当每辆车的月租金定为4
100元时,租赁公司的月收益最大,最大月收益为304
200元.
20.
解:(1)根据奇函数的图象关于原点对称,故函数f(x)的图象如图2.
当x≥0时,设y=a(x﹣1)2﹣2,代入(2,0)得a=2,
即y=2=2x(x﹣1)2=2x2﹣4x.
同理求得当x<0时,设y=﹣2x2﹣4x.
所以.
由图可得函数f(x)的单调递增区间为(﹣∞,﹣1],[1,+∞),
函数f(x)的单调递减区间为[﹣1,1].
(3)由图可得y=f(x)与y=a有三个交点时,﹣2<a<2.
所以方程f(x)=a有三个不同的根,实数a的取值范围是(﹣2,2).
21.解:(1)y=g(t)·f(t)=(80-2t)·(20-|t-10|)=(40-t)(40-|t-10|)=
(2)当0≤t<10时,y的取值范围是[1
200,1
225],
在t=5时,y取得最大值为1
225;
当10≤t≤20时,y的取值范围是[600,1
200],
在t=20时,y取得最小值为600.
所以第5天,日销售额y取得最大值为1
225元;
第20天,日销售额y取得最小值为600元.
22.解:(1)f(x)=,函数f(x)的图象如图3所示.由图象得,函数f(x)的单调递减区间是(0,1),单调增区间是(﹣∞,0),(1,+∞).
(2)作出直线y=m,函数g(x)=f(x)﹣m恰有3个不同零点等价于函数y=m与函数f(x)的图象恰有三个不同公共点.
由函数f(x)=的图象易知.
故m的取值范围为(,1).
