北师大版高中数学必修一第一章集合 单元测试题
文档属性
| 名称 | 北师大版高中数学必修一第一章集合 单元测试题 |  | |
| 格式 | zip | ||
| 文件大小 | 187.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-20 14:23:06 | ||
图片预览


文档简介
第一章
集合
单元测试题
(时间:120分钟
满分150分)
选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列说法正确的是( )
A.很小的实数可以构成集合
B.集合{y|y=x2-1}与集合{(x,y)|y=x2-1}是同一个集合
C.自然数集N中最小的数是1
D.空集是任何集合的子集
2.已知集合A={x|0<x<},B={x|1≤x<2},则A∪B=( )
A.{x|x≤0}
B.{x|x≥2}
C.{x|1≤x<}
D.{x|0<x<2}
3.已知集合M={0,1,2},N={x|x=2a-1,a∈N+},则集合M∩N=( )
A.{0}
B.{1,2}
C.{1}
D.{2}
4.已知集合M={x|x=+,k∈Z},N={x|x=+,k∈Z},若x0∈M,则x0与N的关系是( )
A.x0∈N
B.x0 N
C.x0∈N或x0 N
D.x0 N
5.已知M={y|y=x2+1,x∈R},N={y|y=-x2+1,x∈R},则M∩N=( )
A.{0,1}
B.{(0,1)}
C.{1}
D.以上都不是
6.设全集U和集合A,B,P满足A= UB,B= UP,则A与P的关系是( )
A.A= UP
B.A=P
C.AP
D.AP
7.已知全集U={1,2,3,4,5},集合A={x|x2-3x+2=0},B={x|x=2a,a∈A},则集合 U(A∪B)中元素的个数是( )
A.1个
B.2个
C.3个
D.4个
8.已知集合A={x|a-1≤x≤a+2},B={x|3A.{a|3B.{a|3≤a≤4}
C.{a|3D.
9.设集合A={x||x-a|<1},B={x|1A.{a|0≤a≤6}
B.{a|a≤2或a≥4}
C.{a|a≤0或a≥6}
D.{a|2≤a≤4}
10.已知A,B均为集合U={1,3,5,7,9}的子集,且A∩B={3},( UB)∩A={9},则A等于( )
A.{1,3}
B.{3,7,9}
C.{3,5,9}
D.{3,9}
二、填空题(本大题共5小题,每小题5分,共25分.把答案填在题中横线上)
11.
设集合A={-1,1,3},B={a+2,a2+4},A∩B={3},则实数a=________.
12.如图所示的全集I及集合A,B,C,则阴影部分可用集合的运算表示为____________.
13.设A={x|-2≤x≤4},B={x|x14.已知集合A={1,3,x},B={1,x2},设U为全集,若B∪( UB)=A,则 UB=________.
15.
设U={0,1,2,3},A={x∈U|x2+mx=0},若 UA={1,2},则实数m=________.
三、解答题(本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤)
16.(12分)设集合A={-2},B={x|ax+1=0,a∈R},若A∩B=B,求实数a的值.
17.(12分)设A={x|x2-3x+2=0},B={x|x2-ax+2=0},若A∪B=A,求由a的值组成的集合.
18.(12分)设,,且.
(1)求的值及集合;
(2)设全集,求,并写出的所有子集.
19.(12分)设集合,,且,,,求实数的值.
20.(13分)已知集合,,,全集.
(1)求;
(2)若,求实数的取值范围.
21.(14分)已知集合A={x||x-a|=4},集合B={1,2,b}.
(1)是否存在实数a,使得对于任意实数b都有A B?若存在,求出对应的a;若不存在,试说明理由;
(2)若A B成立,求出对应的实数对(a,b).
参考答案
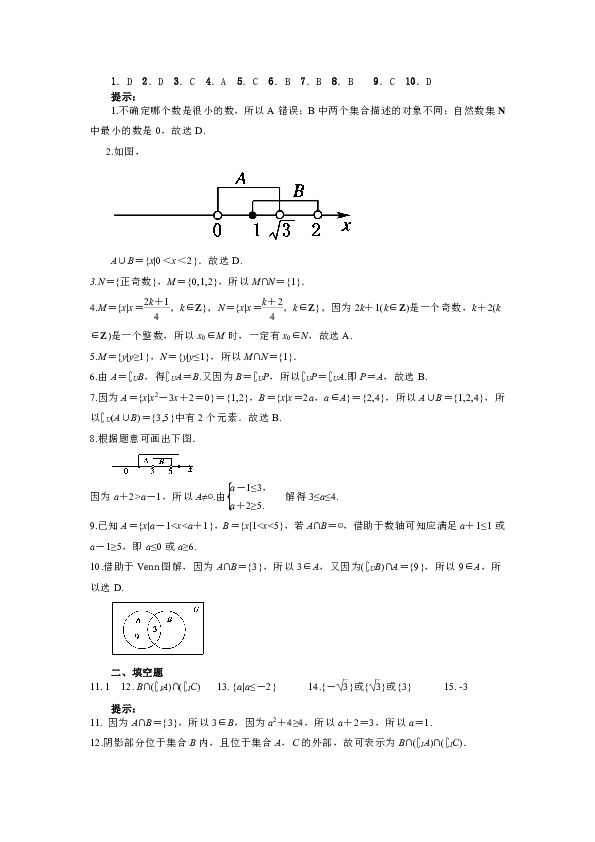
一、选择题
1.D
2.D
3.C
4.A
5.C
6.B
7.B
8.B
9.C
10.D
提示:
1.不确定哪个数是很小的数,所以A错误;B中两个集合描述的对象不同;自然数集N中最小的数是0,故选D.
2.如图,
A∪B={x|0<x<2}.故选D.
3.N={正奇数},M={0,1,2},所以M∩N={1}.
4.M={x|x=,k∈Z},N={x|x=,k∈Z},因为2k+1(k∈Z)是一个奇数,k+2(k∈Z)是一个整数,所以x0∈M时,一定有x0∈N,故选A.
5.M={y|y≥1},N={y|y≤1},所以M∩N={1}.
6.由A= UB,得 UA=B.又因为B= UP,所以 UP= UA.即P=A,故选B.
7.因为A={x|x2-3x+2=0}={1,2},B={x|x=2a,a∈A}={2,4},所以A∪B={1,2,4},所以 U(A∪B)={3,5}中有2个元素.故选B.
8.根据题意可画出下图.
因为a+2>a-1,所以A≠ .由解得3≤a≤4.
9.已知A={x|a-110.借助于Venn图解,因为A∩B={3},所以3∈A,又因为( UB)∩A={9},所以9∈A,所以选D.
二、填空题
11.
1
12.
B∩( IA)∩( IC)
13.
{a|a≤-2}
14.{-}或{}或{3}
15.
-3
提示:
11.
因为A∩B={3},所以3∈B,因为a2+4≥4,所以a+2=3,所以a=1.
12.阴影部分位于集合B内,且位于集合A,C的外部,故可表示为B∩( IA)∩( IC).
13.画出数轴,则a≤-2.
14.因为B∪( UB)=A,所以A=U,所以B A.
(1)当x2=3时,x=±,B={1,3}, UB={}或{-};
(2)当x2=x时,x=0或1.当x=0时,B={0,1}, UB={3};而当x=1不满足集合元素的互异性,舍去.
15.因为 UA={1,2},所以A={0,3},故m=-3.
三、解答题
16.解:因为A∩B=B,所以B A.
因为A={-2}≠ ,所以B= 或B≠ .
当B= 时,方程ax+1=0无实数解,a=0.
当B≠ 时,a≠0,则B={-},
所以-∈A,即有-=-2,得a=.
综上,得a=0或a=.
17.解:由A∪B=A,可知B A,
而A={1,2},故B可为{1,2},{1},{2},或 .
当B={1,2}=A时,显然有a=3.
当B={1},{2},或 时,方程x2-ax+2=0有等根或无实根,故Δ≤0,即a2-8≤0,解得-2≤a≤2.
但当a=±2时,得到B={-}或{},不能满足B A.故所求a值的集合为{3}∪{a|-218.解:(1)因为所以,即10+2a=0,解得a=-5,
从而可知=,=;
(2)由(1)知=所以=所以,
其子集为,,,.
19.解:因为,所以-3A.
将-3代入方程得=-1,从而A={-3,4}.
又,AB,-3B,所以B={-3}.
所以由根与系数的关系知(-3)+(-3)=-b,(-3)(-3)=c,
b=-6,c=9.
20.解:(1).
(2)因为,又,,
所以,解得.
所以实数的取值范围是.
21.解:(1)设存在实数a,使得对任意的实数b,都有A B.
因为A={a+4,a-4},b任意,所以1,2都是A中的元素,,a无实数解.
所以这样的实数a不存在.
(2)因为A B成立,A={a+4,a-4},所以有
或或或,
解得或或或.
所以实数对为(5,9),(6,10),(-3,-7),(-2,-6).
集合
单元测试题
(时间:120分钟
满分150分)
选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列说法正确的是( )
A.很小的实数可以构成集合
B.集合{y|y=x2-1}与集合{(x,y)|y=x2-1}是同一个集合
C.自然数集N中最小的数是1
D.空集是任何集合的子集
2.已知集合A={x|0<x<},B={x|1≤x<2},则A∪B=( )
A.{x|x≤0}
B.{x|x≥2}
C.{x|1≤x<}
D.{x|0<x<2}
3.已知集合M={0,1,2},N={x|x=2a-1,a∈N+},则集合M∩N=( )
A.{0}
B.{1,2}
C.{1}
D.{2}
4.已知集合M={x|x=+,k∈Z},N={x|x=+,k∈Z},若x0∈M,则x0与N的关系是( )
A.x0∈N
B.x0 N
C.x0∈N或x0 N
D.x0 N
5.已知M={y|y=x2+1,x∈R},N={y|y=-x2+1,x∈R},则M∩N=( )
A.{0,1}
B.{(0,1)}
C.{1}
D.以上都不是
6.设全集U和集合A,B,P满足A= UB,B= UP,则A与P的关系是( )
A.A= UP
B.A=P
C.AP
D.AP
7.已知全集U={1,2,3,4,5},集合A={x|x2-3x+2=0},B={x|x=2a,a∈A},则集合 U(A∪B)中元素的个数是( )
A.1个
B.2个
C.3个
D.4个
8.已知集合A={x|a-1≤x≤a+2},B={x|3
C.{a|3
9.设集合A={x||x-a|<1},B={x|1
B.{a|a≤2或a≥4}
C.{a|a≤0或a≥6}
D.{a|2≤a≤4}
10.已知A,B均为集合U={1,3,5,7,9}的子集,且A∩B={3},( UB)∩A={9},则A等于( )
A.{1,3}
B.{3,7,9}
C.{3,5,9}
D.{3,9}
二、填空题(本大题共5小题,每小题5分,共25分.把答案填在题中横线上)
11.
设集合A={-1,1,3},B={a+2,a2+4},A∩B={3},则实数a=________.
12.如图所示的全集I及集合A,B,C,则阴影部分可用集合的运算表示为____________.
13.设A={x|-2≤x≤4},B={x|x
15.
设U={0,1,2,3},A={x∈U|x2+mx=0},若 UA={1,2},则实数m=________.
三、解答题(本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤)
16.(12分)设集合A={-2},B={x|ax+1=0,a∈R},若A∩B=B,求实数a的值.
17.(12分)设A={x|x2-3x+2=0},B={x|x2-ax+2=0},若A∪B=A,求由a的值组成的集合.
18.(12分)设,,且.
(1)求的值及集合;
(2)设全集,求,并写出的所有子集.
19.(12分)设集合,,且,,,求实数的值.
20.(13分)已知集合,,,全集.
(1)求;
(2)若,求实数的取值范围.
21.(14分)已知集合A={x||x-a|=4},集合B={1,2,b}.
(1)是否存在实数a,使得对于任意实数b都有A B?若存在,求出对应的a;若不存在,试说明理由;
(2)若A B成立,求出对应的实数对(a,b).
参考答案
一、选择题
1.D
2.D
3.C
4.A
5.C
6.B
7.B
8.B
9.C
10.D
提示:
1.不确定哪个数是很小的数,所以A错误;B中两个集合描述的对象不同;自然数集N中最小的数是0,故选D.
2.如图,
A∪B={x|0<x<2}.故选D.
3.N={正奇数},M={0,1,2},所以M∩N={1}.
4.M={x|x=,k∈Z},N={x|x=,k∈Z},因为2k+1(k∈Z)是一个奇数,k+2(k∈Z)是一个整数,所以x0∈M时,一定有x0∈N,故选A.
5.M={y|y≥1},N={y|y≤1},所以M∩N={1}.
6.由A= UB,得 UA=B.又因为B= UP,所以 UP= UA.即P=A,故选B.
7.因为A={x|x2-3x+2=0}={1,2},B={x|x=2a,a∈A}={2,4},所以A∪B={1,2,4},所以 U(A∪B)={3,5}中有2个元素.故选B.
8.根据题意可画出下图.
因为a+2>a-1,所以A≠ .由解得3≤a≤4.
9.已知A={x|a-1
二、填空题
11.
1
12.
B∩( IA)∩( IC)
13.
{a|a≤-2}
14.{-}或{}或{3}
15.
-3
提示:
11.
因为A∩B={3},所以3∈B,因为a2+4≥4,所以a+2=3,所以a=1.
12.阴影部分位于集合B内,且位于集合A,C的外部,故可表示为B∩( IA)∩( IC).
13.画出数轴,则a≤-2.
14.因为B∪( UB)=A,所以A=U,所以B A.
(1)当x2=3时,x=±,B={1,3}, UB={}或{-};
(2)当x2=x时,x=0或1.当x=0时,B={0,1}, UB={3};而当x=1不满足集合元素的互异性,舍去.
15.因为 UA={1,2},所以A={0,3},故m=-3.
三、解答题
16.解:因为A∩B=B,所以B A.
因为A={-2}≠ ,所以B= 或B≠ .
当B= 时,方程ax+1=0无实数解,a=0.
当B≠ 时,a≠0,则B={-},
所以-∈A,即有-=-2,得a=.
综上,得a=0或a=.
17.解:由A∪B=A,可知B A,
而A={1,2},故B可为{1,2},{1},{2},或 .
当B={1,2}=A时,显然有a=3.
当B={1},{2},或 时,方程x2-ax+2=0有等根或无实根,故Δ≤0,即a2-8≤0,解得-2≤a≤2.
但当a=±2时,得到B={-}或{},不能满足B A.故所求a值的集合为{3}∪{a|-2
从而可知=,=;
(2)由(1)知=所以=所以,
其子集为,,,.
19.解:因为,所以-3A.
将-3代入方程得=-1,从而A={-3,4}.
又,AB,-3B,所以B={-3}.
所以由根与系数的关系知(-3)+(-3)=-b,(-3)(-3)=c,
b=-6,c=9.
20.解:(1).
(2)因为,又,,
所以,解得.
所以实数的取值范围是.
21.解:(1)设存在实数a,使得对任意的实数b,都有A B.
因为A={a+4,a-4},b任意,所以1,2都是A中的元素,,a无实数解.
所以这样的实数a不存在.
(2)因为A B成立,A={a+4,a-4},所以有
或或或,
解得或或或.
所以实数对为(5,9),(6,10),(-3,-7),(-2,-6).
