2016-2017学年七年级数学下册第6章 数据的分析 测试题(含答案)
文档属性
| 名称 | 2016-2017学年七年级数学下册第6章 数据的分析 测试题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 144.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-19 22:33:55 | ||
图片预览


文档简介
第6章
数据的分析
测试题
一、选择题(每小题3分,共24分)
1.
小麦7次上学所用时间(单位:分)分别为10,7,12,13,8,11,9.这组数据的平均数是(
)
A.
7分
B.
10分
C.11
分
D.
12分
星
期
一
二
三
四
五
六
日
最高气温(℃)
22
24
23
25
24
22
21
2.
小明记录了某地区一星期每天的最高气温如下表:
则这个星期每天的最高气温的中位数是(
)
A.22
℃
B.23
℃
C.
24
℃
D.
25
℃
3.
某校五个绿化小组一天植树的棵数如下:10,10,12,,8.已知这组数据的众数与平均数相等,那么这组数据的中位数是(
)
A.8
B.9
C.10
D.12
4.
一名射击手连续射靶22次,其中3次射中10环,7次射中9环,9次射中8环,3次射中7环,则射中环数的中位数和众数分别为(
)
A.8环,9环
B.8环,8环
C.8.5环,8环
D.8.5环,9环
5.
一组数据6,4,a,3,2的平均数是5,这组数据的方差为( )
A.8
B.5
C.
D.
3
6.
甲、乙两人在相同的条件下,各射靶10次,经过计算:甲、乙的平均数均是7,甲的方差是1.2,乙的方差是5.8,下列说法中不正确的是(
)
A.甲、乙射中的总环数相同
B.甲的成绩稳定
C.乙的成绩波动较大
D.甲、乙的众数相同
7.已知一组数据:-13,-8,-4,2,6,7,9,12,若在这组数据中添加一个数字4组成一组新的数据,则新数据与原来的数据比较(
)
A.中位数和平均数都改变了
B.中位数和平均数都没有变
C.中位数改变了,但平均数没变
D.中位数没变,平均数变了
8.
甲、乙两班举行电脑汉字输入速度比赛,参赛学生每分钟输入汉字的个数经统计计算后结果如下表:
班级
参加人数
中位数
方差
平均数
甲
55
149
191
135
乙
55
151
110
135
某同学根据上表分析得出如下结论:
①甲、乙两班学生成绩的平均水平相同;
②乙班优秀的人数多于甲班优秀的人数;(每分钟输入汉字不少于150个为优秀)
③甲班成绩的波动情况比乙班成绩的波动小.
上述结论中正确的是(
)
A.①②③
B.①②
C.①③
D.②③
二、填空题(每小题4分,共32分)
9.
小斌所在的课外活动小组在大课间活动中练习立定跳远,成绩(单位:米)如下:1.96,2.16,2.04,2.20,1.98,2.22,2.32,则这组数据的中位数是 米.
10.
在演唱比赛中,8位评委给一名歌手的演唱打分如下:9.3,9.5,9.9,9.4,9.3,8.9,9.2,9.6,若去掉一个最高分和一个最低分后的平均分为得分,则这名歌手最后得分约为________.(精确到0.1)
11.
10月1日是中华人民共和国成立纪念日,要从某校选择256名身高基本相同的女同学组成表演方阵,在这个问题中我们最值得关注的是该校所有女生身高的___.(填“平均数”“中位数”或“众数”)
12.
若已知数据的平均数为,那么数据的平均数为_______.(用含的表达式表示)
13.
甲、乙两人进行射击测试,每人10次射击成绩的平均数都是8.5环,方差分别是:=2,=1.5,则射击成绩较稳定的是
.(填“甲”或“乙”)
14.
某校五个绿化小组一天植树的棵数分别为10,10,12,x,8.已知这组数据的平均数是10,那么这组数据的方差是 .
15.
为了了解贯彻执行国家提倡的“阳光体育运动”的实施情况,将某班50名同学一周的体育锻炼情况绘制成图1所示的条形统计图,根据统计图提供的数据,该班50名同学一周参加体育锻炼时间的中位数与众数之和为___h.
16.
某同学5次上学途中所花的时间(单位:分)分别为x,y,10,11,9,已知这组数据的平均数为10,方差为2,则|x-y|的值为___.
三、解答题(共64分)
17.(12分)某瓜农用大棚栽培技术种植了一亩地的良种西瓜,这亩地产西瓜约600个,在西瓜上市前瓜农随机摘了10个成熟的西瓜,称得质量如下表所示:
西瓜质量(千克)
5.5
5.4
5.0
4.9
4.6
4.3
西瓜数量(个)
1
2
3
2
1
1
计算这10个西瓜的平均质量,并根据计算结果估计这亩地的西瓜产量约是多少千克?
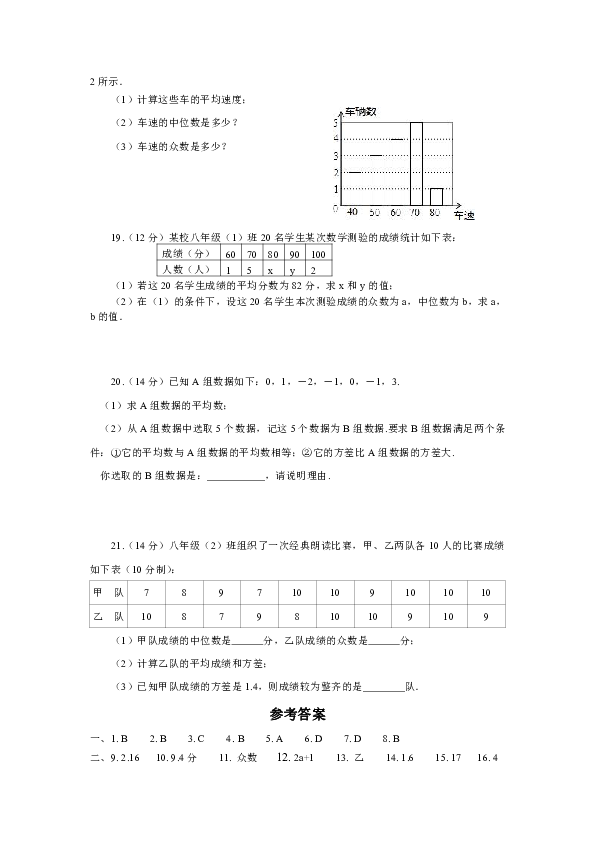
18.(12分)交警在一个路口统计某个时段来往车辆的车速(单位:千米/时)情况如图2所示.
(1)计算这些车的平均速度;
(2)车速的中位数是多少?
(3)车速的众数是多少?
19.(12分)某校八年级(1)班20名学生某次数学测验的成绩统计如下表:
成绩(分)
60
70
80
90
100
人数(人)
1
5
x
y
2
(1)若这20名学生成绩的平均分数为82分,求x和y的值;
(2)在(1)的条件下,设这20名学生本次测验成绩的众数为a,中位数为b,求a,b的值.
20.(14分)已知A组数据如下:0,1,-2,-1,0,-1,3.
(1)求A组数据的平均数;
(2)从A组数据中选取5个数据,记这5个数据为B组数据.要求B组数据满足两个条件:①它的平均数与A组数据的平均数相等;②它的方差比A组数据的方差大.
你选取的B组数据是:
,请说明理由.
21.(14分)八年级(2)班组织了一次经典朗读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲
队
7
8
9
7
10
10
9
10
10
10
乙
队
10
8
7
9
8
10
10
9
10
9
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队.
参考答案
一、1.
B
2.
B
3.
C
4.
B
5.
A
6.
D
7.
D
8.
B
二、9.
2.16
10.
9.4分
11.
众数
12.
2a+1
13.
乙
14.
1.6
15.
17
16.
4
三、17.
解:这10个西瓜的平均质量为
=5.0(千克).
所以这亩地的西瓜质量约为5×600=3000(千克).
18.
解:(1)这些车的平均速度是(40×2+50×3+60×4+70×5+80×1)÷15=60(千米/时).
(2)共有15个数据,按顺序排列后第8个数是60,则中位数是60千米/时.
(3)70出现的次数最多,则车速的众数是70千米/时.
19.(1)x=5,y=7;(2)a=90,b=80.
20.
解:(1)由条件,得A组数据的平均数=×(0+1-2-1+0-1+3)=0.
(2)答案不唯一.如,选取的B组数据是:1,-2,-1,-1,3.
理由:因为=×(1-2-1-1+3)=0,所以=.
=×(02+12+22+12+02+12+32)=,=×(12+22+12+12+32)=.
因为<,所以数据1,-2,-1,-1,3符合题意.
21.
解:(1)9.5
10
提示:把甲队的成绩从小到大排列为:7,7,8,9,9,10,10,10,10,10,最中间两个数的平均数是(9+10)÷2=9.5(分),则中位数是9.5分;
10出现了4次,出现的次数最多,则乙队成绩的众数是10分.
(2)乙队的平均成绩是(10×4+8×2+7+9×3)=9,
方差是[4×(10﹣9)2+2×(8﹣9)2+(7﹣9)2+3×(9﹣9)2]=1.
(3)乙
图1
数据的分析
测试题
一、选择题(每小题3分,共24分)
1.
小麦7次上学所用时间(单位:分)分别为10,7,12,13,8,11,9.这组数据的平均数是(
)
A.
7分
B.
10分
C.11
分
D.
12分
星
期
一
二
三
四
五
六
日
最高气温(℃)
22
24
23
25
24
22
21
2.
小明记录了某地区一星期每天的最高气温如下表:
则这个星期每天的最高气温的中位数是(
)
A.22
℃
B.23
℃
C.
24
℃
D.
25
℃
3.
某校五个绿化小组一天植树的棵数如下:10,10,12,,8.已知这组数据的众数与平均数相等,那么这组数据的中位数是(
)
A.8
B.9
C.10
D.12
4.
一名射击手连续射靶22次,其中3次射中10环,7次射中9环,9次射中8环,3次射中7环,则射中环数的中位数和众数分别为(
)
A.8环,9环
B.8环,8环
C.8.5环,8环
D.8.5环,9环
5.
一组数据6,4,a,3,2的平均数是5,这组数据的方差为( )
A.8
B.5
C.
D.
3
6.
甲、乙两人在相同的条件下,各射靶10次,经过计算:甲、乙的平均数均是7,甲的方差是1.2,乙的方差是5.8,下列说法中不正确的是(
)
A.甲、乙射中的总环数相同
B.甲的成绩稳定
C.乙的成绩波动较大
D.甲、乙的众数相同
7.已知一组数据:-13,-8,-4,2,6,7,9,12,若在这组数据中添加一个数字4组成一组新的数据,则新数据与原来的数据比较(
)
A.中位数和平均数都改变了
B.中位数和平均数都没有变
C.中位数改变了,但平均数没变
D.中位数没变,平均数变了
8.
甲、乙两班举行电脑汉字输入速度比赛,参赛学生每分钟输入汉字的个数经统计计算后结果如下表:
班级
参加人数
中位数
方差
平均数
甲
55
149
191
135
乙
55
151
110
135
某同学根据上表分析得出如下结论:
①甲、乙两班学生成绩的平均水平相同;
②乙班优秀的人数多于甲班优秀的人数;(每分钟输入汉字不少于150个为优秀)
③甲班成绩的波动情况比乙班成绩的波动小.
上述结论中正确的是(
)
A.①②③
B.①②
C.①③
D.②③
二、填空题(每小题4分,共32分)
9.
小斌所在的课外活动小组在大课间活动中练习立定跳远,成绩(单位:米)如下:1.96,2.16,2.04,2.20,1.98,2.22,2.32,则这组数据的中位数是 米.
10.
在演唱比赛中,8位评委给一名歌手的演唱打分如下:9.3,9.5,9.9,9.4,9.3,8.9,9.2,9.6,若去掉一个最高分和一个最低分后的平均分为得分,则这名歌手最后得分约为________.(精确到0.1)
11.
10月1日是中华人民共和国成立纪念日,要从某校选择256名身高基本相同的女同学组成表演方阵,在这个问题中我们最值得关注的是该校所有女生身高的___.(填“平均数”“中位数”或“众数”)
12.
若已知数据的平均数为,那么数据的平均数为_______.(用含的表达式表示)
13.
甲、乙两人进行射击测试,每人10次射击成绩的平均数都是8.5环,方差分别是:=2,=1.5,则射击成绩较稳定的是
.(填“甲”或“乙”)
14.
某校五个绿化小组一天植树的棵数分别为10,10,12,x,8.已知这组数据的平均数是10,那么这组数据的方差是 .
15.
为了了解贯彻执行国家提倡的“阳光体育运动”的实施情况,将某班50名同学一周的体育锻炼情况绘制成图1所示的条形统计图,根据统计图提供的数据,该班50名同学一周参加体育锻炼时间的中位数与众数之和为___h.
16.
某同学5次上学途中所花的时间(单位:分)分别为x,y,10,11,9,已知这组数据的平均数为10,方差为2,则|x-y|的值为___.
三、解答题(共64分)
17.(12分)某瓜农用大棚栽培技术种植了一亩地的良种西瓜,这亩地产西瓜约600个,在西瓜上市前瓜农随机摘了10个成熟的西瓜,称得质量如下表所示:
西瓜质量(千克)
5.5
5.4
5.0
4.9
4.6
4.3
西瓜数量(个)
1
2
3
2
1
1
计算这10个西瓜的平均质量,并根据计算结果估计这亩地的西瓜产量约是多少千克?
18.(12分)交警在一个路口统计某个时段来往车辆的车速(单位:千米/时)情况如图2所示.
(1)计算这些车的平均速度;
(2)车速的中位数是多少?
(3)车速的众数是多少?
19.(12分)某校八年级(1)班20名学生某次数学测验的成绩统计如下表:
成绩(分)
60
70
80
90
100
人数(人)
1
5
x
y
2
(1)若这20名学生成绩的平均分数为82分,求x和y的值;
(2)在(1)的条件下,设这20名学生本次测验成绩的众数为a,中位数为b,求a,b的值.
20.(14分)已知A组数据如下:0,1,-2,-1,0,-1,3.
(1)求A组数据的平均数;
(2)从A组数据中选取5个数据,记这5个数据为B组数据.要求B组数据满足两个条件:①它的平均数与A组数据的平均数相等;②它的方差比A组数据的方差大.
你选取的B组数据是:
,请说明理由.
21.(14分)八年级(2)班组织了一次经典朗读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲
队
7
8
9
7
10
10
9
10
10
10
乙
队
10
8
7
9
8
10
10
9
10
9
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队.
参考答案
一、1.
B
2.
B
3.
C
4.
B
5.
A
6.
D
7.
D
8.
B
二、9.
2.16
10.
9.4分
11.
众数
12.
2a+1
13.
乙
14.
1.6
15.
17
16.
4
三、17.
解:这10个西瓜的平均质量为
=5.0(千克).
所以这亩地的西瓜质量约为5×600=3000(千克).
18.
解:(1)这些车的平均速度是(40×2+50×3+60×4+70×5+80×1)÷15=60(千米/时).
(2)共有15个数据,按顺序排列后第8个数是60,则中位数是60千米/时.
(3)70出现的次数最多,则车速的众数是70千米/时.
19.(1)x=5,y=7;(2)a=90,b=80.
20.
解:(1)由条件,得A组数据的平均数=×(0+1-2-1+0-1+3)=0.
(2)答案不唯一.如,选取的B组数据是:1,-2,-1,-1,3.
理由:因为=×(1-2-1-1+3)=0,所以=.
=×(02+12+22+12+02+12+32)=,=×(12+22+12+12+32)=.
因为<,所以数据1,-2,-1,-1,3符合题意.
21.
解:(1)9.5
10
提示:把甲队的成绩从小到大排列为:7,7,8,9,9,10,10,10,10,10,最中间两个数的平均数是(9+10)÷2=9.5(分),则中位数是9.5分;
10出现了4次,出现的次数最多,则乙队成绩的众数是10分.
(2)乙队的平均成绩是(10×4+8×2+7+9×3)=9,
方差是[4×(10﹣9)2+2×(8﹣9)2+(7﹣9)2+3×(9﹣9)2]=1.
(3)乙
图1
