2016—2017学年华师大版九年级数学下册第27章圆 检测题(含答案)
文档属性
| 名称 | 2016—2017学年华师大版九年级数学下册第27章圆 检测题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 329.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-19 22:40:25 | ||
图片预览

文档简介
第27章圆
检测题
(时间:90分钟,满分120分)
班级
姓名
得分
一、选择题(每小题3分,共30分)
1.
三角形的外心是
( )
A.
三条中线的交点
B.
三个内角的角平分线的交点
C.
三条边的垂直平分线的交点
D.
三条高的交点
2.
Rt△ABC中,∠C=90°,AC=3
cm,BC=4
cm,以C为圆心,r为半径作圆,若圆C与直线AB相切,则r的值为
( )
A.
2
cm
B.
2.4
cm
C.
3
cm
D.
4
cm
3.
若P为半径长是6cm的⊙O内一点,OP=2cm,则过P点的最短的弦长为
( )
A.12cm
B.2cm
C.4cm
D.8cm
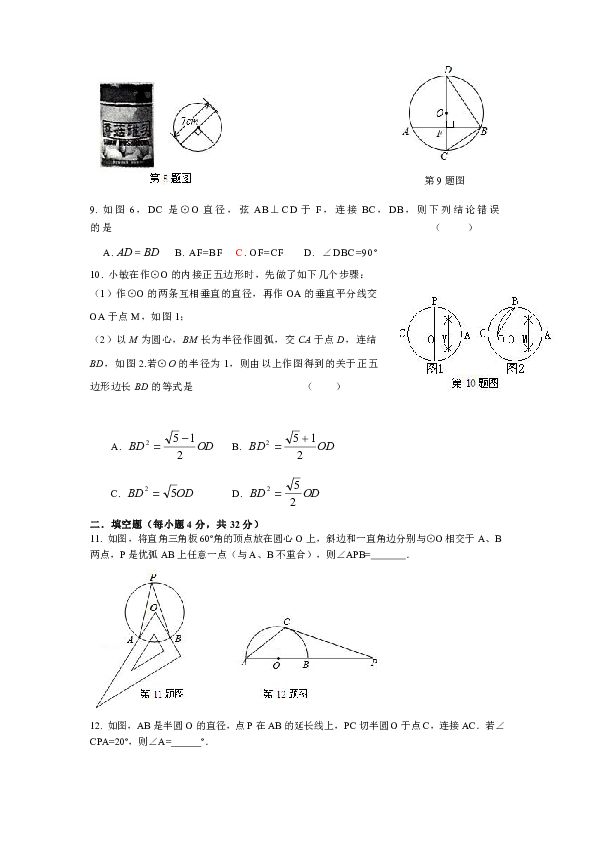
4.
如图,AB是⊙O的直径,∠AOC=110°,则∠D等于
( )
A.25°
B.35°
C.55°
D.70°
5.
如图,要拧开一个边长为a=6mm的正六边形螺帽,扳手张开的开口b至少为
(
)
A.
B.12
mm
C.
D.
6.
如图,AB为⊙O的直径,C为⊙O外一点,过点C作的⊙O切线,切点为B,连接AC交⊙O于D,∠C=38°.点E在AB右侧的半圆上运动(不与A、B重合),则∠AED的大小是
( )
A.19°
B.32°
C.
38°
D.76°
7.
直线AB与⊙O相切于B点,C是⊙O与OA的交点,点D是⊙O上的动点(D与B,C不重合),若∠A=40°,则∠BDC的度数是
( )
A.
25°或155°
B.
50°或155°
C.
25°或130°
D.
50°或130°
8.
如图,某厂生产横截面直径为7cm的圆柱形罐头,需将“蘑菇罐头”字样贴在罐头侧面.为了获得较佳视觉效果,字样在罐头侧面所形成的弧的所对的圆心角度数为90°,则“蘑菇罐头”字样的长度为
( )
A.
cm
B.
cm
C.
cm
D.
cm
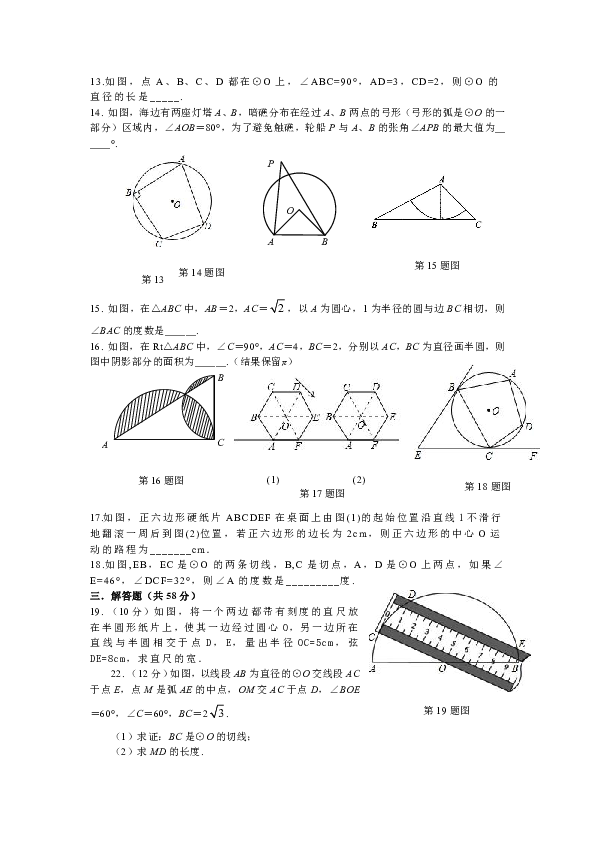
9.
如图6,DC 是⊙O直径,弦AB⊥CD于F,连接BC,DB,则下列结论错误的是
( )
A.=
B.
AF=BF
C.
OF=CF
D.
∠DBC=90°
10.
小敏在作⊙O的内接正五边形时,先做了如下几个步骤:
(1)作⊙O的两条互相垂直的直径,再作OA的垂直平分线交OA于点M,如图1;
(2)以M为圆心,BM长为半径作圆弧,交CA于点D,连结BD,如图2.若⊙O的半径为1,则由以上作图得到的关于正五边形边长BD的等式是
(
)
A.
B.
C.
D.
二.填空题(每小题4分,共32分)
11.
如图,将直角三角板60°角的顶点放在圆心O上,斜边和一直角边分别与⊙O相交于A、B两点,P是优弧AB上任意一点(与A、B不重合),则∠APB=
.
12.
如图,AB是半圆O的直径,点P在AB的延长线上,PC切半圆O于点C,连接AC.若∠CPA=20°,则∠A=
°.
13.如图,点A、B、C、D都在⊙O上,∠ABC=90°,AD=3,CD=2,则⊙O的直径的长是_____.
14.
如图,海边有两座灯塔A、B,暗礁分布在经过A、B两点的弓形(弓形的弧是⊙O的一部分)区域内,∠AOB=80°,为了避免触礁,轮船P与A、B的张角∠APB的最大值为___°.
15.
如图,在△ABC中,AB=2,AC=,以A为圆心,1为半径的圆与边BC相切,则∠BAC的度数是___.
16.
如图,在Rt△ABC中,∠C=90°,AC=4,BC=2,分别以AC,BC为直径画半圆,则图中阴影部分的面积为___.(结果保留π)
17.如图,正六边形硬纸片ABCDEF在桌面上由图(1)的起始位置沿直线l不滑行地翻滚一周后到图(2)位置,若正六边形的边长为2cm,则正六边形的中心O运动的路程为_______cm.
18.如图,EB,EC是⊙O的两条切线,B,C是切点,A,D是⊙O上两点,如果∠E=46°,∠DCF=32°,则∠A的度数是_________度.
三.解答题(共58分)
19.
(10分)如图,将一个两边都带有刻度的直尺放在半圆形纸片上,使其一边经过圆心O,另一边所在直线与半圆相交于点D,E,量出半径OC=5cm,弦DE=8cm,求直尺的宽.
22.
(12分)如图,以线段AB为直径的⊙O交线段AC于点E,点M是弧AE的中点,OM交AC于点D,∠BOE=60°,∠C=60°,BC=2.
(1)求证:BC是⊙O的切线;
(2)求MD的长度.
20.(12分)如图,△OAB的底边AB经过⊙O上的点C,且OA=OB,CA=CB,⊙O与OA、OB分别交于D,E两点.
(1)求证:AB是⊙O的切线.
(2)若D为OA的中点,阴影部分的面积为-,求⊙O的半径r.
21.
(12分)如图,在△ABC中,AB=AC,∠BAC=54°,以AB为直径的⊙O分别交AC,BC于点D,E,过点B作⊙O的切线,交AC的延长线于点F.
(1)求证:BE=CE;
(2)求∠CBF的度数;
若AB=6,求的长.
23.
(14分).如图,⊙O的半径为1,直线CD经过圆心O,交⊙O于C,D两点,直径AB⊥CD,点M是直线CD上异于点C,O,D的一个动点,AM所在的直线交于⊙O于点N,点P是直线CD上另一点,且PM=PN.
(1)当点M在⊙O内部,如图,试判断PN与⊙O的关系,并写出证明过程;
(2)当点M在⊙O外部,如图,其它条件不变时,(1)的结论是否还成立?请说明理由;
(3)当点M在⊙O外部,如图,∠AMO=15°,求图中阴影部分的面积.
参考答案
一.1.
C
2.B
3.
D
4.
B
5.
C
6.
C
7.
A
8.
B
9.
C
10.
C
二.11.
30°
12.
35
13.
14.
40°
15.
105°
16.
17.
4π
18.
99
三.19.
解:过点O作OM⊥DE于点M,连接OD.
∴DM=DE.
∵DE=8(cm)
∴DM=4(cm).
在Rt△ODM中,∵OD=OC=5(cm),
∴OM=.
∴直尺的宽度为3cm.
20.
解:(1)∵∠BOE=60°,
∴∠A=∠BOE=30°.
在△ABC中,∠C=60°,∠A=30°,
∴∠ABC=90°,即AB⊥BC,
∴BC是⊙O的切线.
∵点M是弧AE的中点,
∴OM⊥AE,
在Rt△ABC中,∵BC=2,∠A=30°,
∴AB=6,
∴OA=AB=3,
∴OD=OA=,
∴MD=.
21.(1)连接OC.
.∵OA=OB,CA=CB,
∴OC⊥AB,
∴AB是⊙O的切线.
连接CD.
∵D为OA的中点,OD=OC=r,
∴OA=2OC=2r,
∴∠A=30°,∠AOC=60°,AC=r.
∴∠AOB=120°,AB=2r.
∴S阴=S△AOB-S扇形ODE=AB×OC-=×2r×r-=(-)r2,
∴(-)r2=-
∴r2=1.
而r>0,
∴r=1.
22.
解:(1)连接AE,
∵AB是⊙O直径,
∴∠AEB=90°,即AE⊥BC,
∵AB=AC,
∴BE=CE.
(2)∵∠BAC=54°,AB=AC,
∴∠ABC=63°,
∵BF是⊙O切线,
∴∠ABF=90°,
∴∠CBF=∠ABF﹣∠ABC=27°.
(3)连接OD,
∵OA=OD,∠BAC=54°,
∴∠AOD=72°,
∵AB=6,
∴OA=3,
∴弧AD的长是
( http: / / www.21cnjy.com"
\o
"欢迎登陆21世纪教育网 )=.
23.
解:(1)PN与⊙O相切.
证明:连接ON,则∠ONA=∠OAN.
∵PM=PN,
∴∠PNM=∠PMN.
∵∠AMO=∠PMN,
∴∠PNM=∠AMO.
∴∠PNO=∠PNM+∠ONA=∠AMO+∠OAN=90°.
∴PN与⊙O相切.
(2)成立.
证明:连接ON,则∠ONA=∠OAN.
∵PM=PN,
∴∠PNM=∠PMN.
∴∠OMA+∠OAM=90°,
∴∠PNM+∠ONA=90°.
∴∠PNO=180°-90°=90°,
∴PN与⊙O相切.
(3)
解:连接ON,由(2)可知∠ONP=90°.
∵∠AMO=15°,PM=PN,
∴∠PNM=15°,∠OPN=30°,
∴∠PON=60°,∠AON=30°.
作NE⊥OD,垂足为点E,则NE=.
S阴影=S△AOC+S扇AON-S△CON
=OC OA+×π×12 CO NE
=×1×1+π-×1×
=+π-.
第6题图
第4题图
第9题图
第13题图
A
B
O
P
第15题图
第14题图
C
A
B
第18题图
(2)
第17题图
第16题图
第19题图
O
B
A
C
E
M
D
第21题图
第22题图
第20题图
第23题图
检测题
(时间:90分钟,满分120分)
班级
姓名
得分
一、选择题(每小题3分,共30分)
1.
三角形的外心是
( )
A.
三条中线的交点
B.
三个内角的角平分线的交点
C.
三条边的垂直平分线的交点
D.
三条高的交点
2.
Rt△ABC中,∠C=90°,AC=3
cm,BC=4
cm,以C为圆心,r为半径作圆,若圆C与直线AB相切,则r的值为
( )
A.
2
cm
B.
2.4
cm
C.
3
cm
D.
4
cm
3.
若P为半径长是6cm的⊙O内一点,OP=2cm,则过P点的最短的弦长为
( )
A.12cm
B.2cm
C.4cm
D.8cm
4.
如图,AB是⊙O的直径,∠AOC=110°,则∠D等于
( )
A.25°
B.35°
C.55°
D.70°
5.
如图,要拧开一个边长为a=6mm的正六边形螺帽,扳手张开的开口b至少为
(
)
A.
B.12
mm
C.
D.
6.
如图,AB为⊙O的直径,C为⊙O外一点,过点C作的⊙O切线,切点为B,连接AC交⊙O于D,∠C=38°.点E在AB右侧的半圆上运动(不与A、B重合),则∠AED的大小是
( )
A.19°
B.32°
C.
38°
D.76°
7.
直线AB与⊙O相切于B点,C是⊙O与OA的交点,点D是⊙O上的动点(D与B,C不重合),若∠A=40°,则∠BDC的度数是
( )
A.
25°或155°
B.
50°或155°
C.
25°或130°
D.
50°或130°
8.
如图,某厂生产横截面直径为7cm的圆柱形罐头,需将“蘑菇罐头”字样贴在罐头侧面.为了获得较佳视觉效果,字样在罐头侧面所形成的弧的所对的圆心角度数为90°,则“蘑菇罐头”字样的长度为
( )
A.
cm
B.
cm
C.
cm
D.
cm
9.
如图6,DC 是⊙O直径,弦AB⊥CD于F,连接BC,DB,则下列结论错误的是
( )
A.=
B.
AF=BF
C.
OF=CF
D.
∠DBC=90°
10.
小敏在作⊙O的内接正五边形时,先做了如下几个步骤:
(1)作⊙O的两条互相垂直的直径,再作OA的垂直平分线交OA于点M,如图1;
(2)以M为圆心,BM长为半径作圆弧,交CA于点D,连结BD,如图2.若⊙O的半径为1,则由以上作图得到的关于正五边形边长BD的等式是
(
)
A.
B.
C.
D.
二.填空题(每小题4分,共32分)
11.
如图,将直角三角板60°角的顶点放在圆心O上,斜边和一直角边分别与⊙O相交于A、B两点,P是优弧AB上任意一点(与A、B不重合),则∠APB=
.
12.
如图,AB是半圆O的直径,点P在AB的延长线上,PC切半圆O于点C,连接AC.若∠CPA=20°,则∠A=
°.
13.如图,点A、B、C、D都在⊙O上,∠ABC=90°,AD=3,CD=2,则⊙O的直径的长是_____.
14.
如图,海边有两座灯塔A、B,暗礁分布在经过A、B两点的弓形(弓形的弧是⊙O的一部分)区域内,∠AOB=80°,为了避免触礁,轮船P与A、B的张角∠APB的最大值为___°.
15.
如图,在△ABC中,AB=2,AC=,以A为圆心,1为半径的圆与边BC相切,则∠BAC的度数是___.
16.
如图,在Rt△ABC中,∠C=90°,AC=4,BC=2,分别以AC,BC为直径画半圆,则图中阴影部分的面积为___.(结果保留π)
17.如图,正六边形硬纸片ABCDEF在桌面上由图(1)的起始位置沿直线l不滑行地翻滚一周后到图(2)位置,若正六边形的边长为2cm,则正六边形的中心O运动的路程为_______cm.
18.如图,EB,EC是⊙O的两条切线,B,C是切点,A,D是⊙O上两点,如果∠E=46°,∠DCF=32°,则∠A的度数是_________度.
三.解答题(共58分)
19.
(10分)如图,将一个两边都带有刻度的直尺放在半圆形纸片上,使其一边经过圆心O,另一边所在直线与半圆相交于点D,E,量出半径OC=5cm,弦DE=8cm,求直尺的宽.
22.
(12分)如图,以线段AB为直径的⊙O交线段AC于点E,点M是弧AE的中点,OM交AC于点D,∠BOE=60°,∠C=60°,BC=2.
(1)求证:BC是⊙O的切线;
(2)求MD的长度.
20.(12分)如图,△OAB的底边AB经过⊙O上的点C,且OA=OB,CA=CB,⊙O与OA、OB分别交于D,E两点.
(1)求证:AB是⊙O的切线.
(2)若D为OA的中点,阴影部分的面积为-,求⊙O的半径r.
21.
(12分)如图,在△ABC中,AB=AC,∠BAC=54°,以AB为直径的⊙O分别交AC,BC于点D,E,过点B作⊙O的切线,交AC的延长线于点F.
(1)求证:BE=CE;
(2)求∠CBF的度数;
若AB=6,求的长.
23.
(14分).如图,⊙O的半径为1,直线CD经过圆心O,交⊙O于C,D两点,直径AB⊥CD,点M是直线CD上异于点C,O,D的一个动点,AM所在的直线交于⊙O于点N,点P是直线CD上另一点,且PM=PN.
(1)当点M在⊙O内部,如图,试判断PN与⊙O的关系,并写出证明过程;
(2)当点M在⊙O外部,如图,其它条件不变时,(1)的结论是否还成立?请说明理由;
(3)当点M在⊙O外部,如图,∠AMO=15°,求图中阴影部分的面积.
参考答案
一.1.
C
2.B
3.
D
4.
B
5.
C
6.
C
7.
A
8.
B
9.
C
10.
C
二.11.
30°
12.
35
13.
14.
40°
15.
105°
16.
17.
4π
18.
99
三.19.
解:过点O作OM⊥DE于点M,连接OD.
∴DM=DE.
∵DE=8(cm)
∴DM=4(cm).
在Rt△ODM中,∵OD=OC=5(cm),
∴OM=.
∴直尺的宽度为3cm.
20.
解:(1)∵∠BOE=60°,
∴∠A=∠BOE=30°.
在△ABC中,∠C=60°,∠A=30°,
∴∠ABC=90°,即AB⊥BC,
∴BC是⊙O的切线.
∵点M是弧AE的中点,
∴OM⊥AE,
在Rt△ABC中,∵BC=2,∠A=30°,
∴AB=6,
∴OA=AB=3,
∴OD=OA=,
∴MD=.
21.(1)连接OC.
.∵OA=OB,CA=CB,
∴OC⊥AB,
∴AB是⊙O的切线.
连接CD.
∵D为OA的中点,OD=OC=r,
∴OA=2OC=2r,
∴∠A=30°,∠AOC=60°,AC=r.
∴∠AOB=120°,AB=2r.
∴S阴=S△AOB-S扇形ODE=AB×OC-=×2r×r-=(-)r2,
∴(-)r2=-
∴r2=1.
而r>0,
∴r=1.
22.
解:(1)连接AE,
∵AB是⊙O直径,
∴∠AEB=90°,即AE⊥BC,
∵AB=AC,
∴BE=CE.
(2)∵∠BAC=54°,AB=AC,
∴∠ABC=63°,
∵BF是⊙O切线,
∴∠ABF=90°,
∴∠CBF=∠ABF﹣∠ABC=27°.
(3)连接OD,
∵OA=OD,∠BAC=54°,
∴∠AOD=72°,
∵AB=6,
∴OA=3,
∴弧AD的长是
( http: / / www.21cnjy.com"
\o
"欢迎登陆21世纪教育网 )=.
23.
解:(1)PN与⊙O相切.
证明:连接ON,则∠ONA=∠OAN.
∵PM=PN,
∴∠PNM=∠PMN.
∵∠AMO=∠PMN,
∴∠PNM=∠AMO.
∴∠PNO=∠PNM+∠ONA=∠AMO+∠OAN=90°.
∴PN与⊙O相切.
(2)成立.
证明:连接ON,则∠ONA=∠OAN.
∵PM=PN,
∴∠PNM=∠PMN.
∴∠OMA+∠OAM=90°,
∴∠PNM+∠ONA=90°.
∴∠PNO=180°-90°=90°,
∴PN与⊙O相切.
(3)
解:连接ON,由(2)可知∠ONP=90°.
∵∠AMO=15°,PM=PN,
∴∠PNM=15°,∠OPN=30°,
∴∠PON=60°,∠AON=30°.
作NE⊥OD,垂足为点E,则NE=.
S阴影=S△AOC+S扇AON-S△CON
=OC OA+×π×12 CO NE
=×1×1+π-×1×
=+π-.
第6题图
第4题图
第9题图
第13题图
A
B
O
P
第15题图
第14题图
C
A
B
第18题图
(2)
第17题图
第16题图
第19题图
O
B
A
C
E
M
D
第21题图
第22题图
第20题图
第23题图
