1.6完全平方公式同步练习(解析版)
文档属性
| 名称 | 1.6完全平方公式同步练习(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 102.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-20 09:02:28 | ||
图片预览

文档简介
1.6完全平方公式
同步练习
一、单选题
1、下列关系式中,正确的是(?? )
A、(a﹣b)2=a2﹣b2 B、(a+b)(a﹣b)=a2﹣b2 C、(a+b)2=a2+b2 D、(a+b)2=a2﹣2ab+b221·世纪*教育网
2、已知a+b=4,x+y=10,则a2+2ab+b2﹣x﹣y的值是(?? )
A、6 B、14 C、﹣6 D、4
3、已知a+b=3,ab=2,则a2+b2的值为(?? )
A、3 B、4 C、5 D、6
4、已知a+ =3,则a2+ 的值是(?? )
A、9 B、7 C、5 D、3
5、若(ax+3y)2=4x2﹣12xy+by2 ,则a,b的值分别为(?? )
A、2,9 B、2,﹣9 C、﹣2,9 D、﹣4,9
6、若关于x的二次三项式x2﹣ax+36是一个完全平方式,那么a的值是(?? )
A、12 B、±12 C、6 D、±6
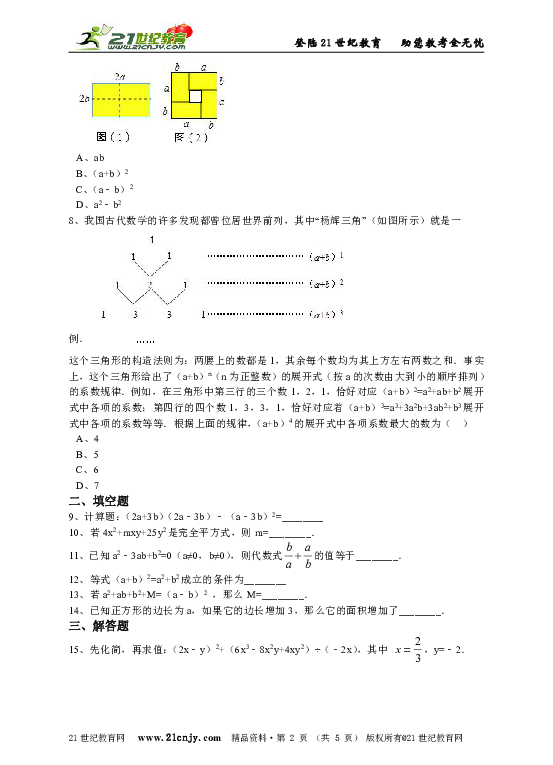
7、如图(1),是一个长为2a宽为2b(a>b)的矩形,用剪刀沿矩形的两条对角轴剪开,把它分成四个全等的小矩形,然后按图(2)拼成一个新的正方形,则中间空白部分的面积是(?? )【来源:21·世纪·教育·网】
A、ab? B、(a+b)2? C、(a﹣b)2? D、a2﹣b2
8、我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”(如图所示)就是一例. 这个三角形的构造法则为:两腰上的数都是1,其余每个数均为其上方左右两数之和.事实上,这个三角形给出了(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应(a+b)2=a2+ab+b2展开式中各项的系数;第四行的四个数1,3,3,1,恰好对应着(a+b)3=a3+3a2b+3ab2+b3展开式中各项的系数等等.根据上面的规律,(a+b)4的展开式中各项系数最大的数为(?? )
A、4 B、5 C、6 D、7
二、填空题
9、计算题:(2a+3b)(2a﹣3b)﹣(a﹣3b)2=________?
10、若4x2+mxy+25y2是完全平方式,则m=________.
11、已知a2﹣3ab+b2=0(a≠0,b≠0),则代数式的值等于________.
12、等式(a+b)2=a2+b2成立的条件为________
13、若a2+ab+b2+M=(a﹣b)2 ,那么M=________.
14、已知正方形的边长为a,如果它的边长增加3,那么它的面积增加了________.
三、解答题
15、先化简,再求值:(2x﹣y)2+(6x3﹣8x2y+4xy2)÷(﹣2x),其中 ,y=﹣2.
16、某大学进行绿地改造,原有一正方形绿地,现将它每边都增加3m,则面积增加了63m2 . 问:原绿地的边长为多少? www-2-1-cnjy-com
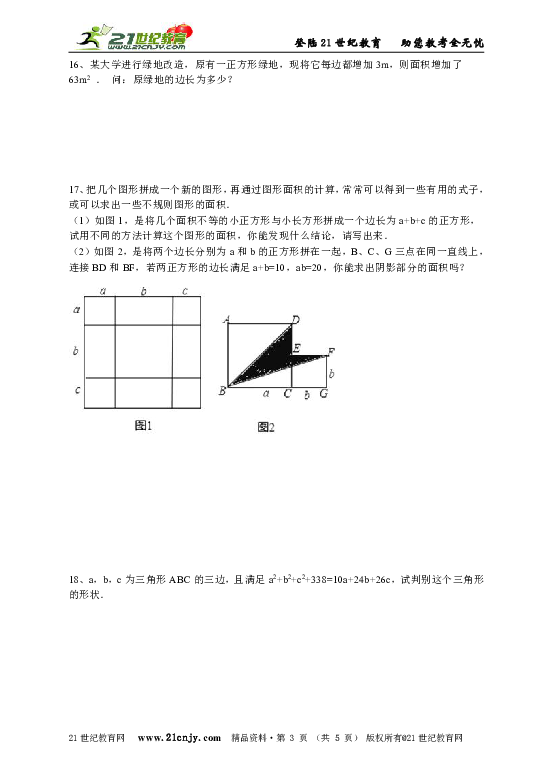
17、把几个图形拼成一个新的图形,再通过图形面积的计算,常常可以得到一些有用的式子,或可以求出一些不规则图形的面积. (1)如图1,是将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形,试用不同的方法计算这个图形的面积,你能发现什么结论,请写出来. (2)如图2,是将两个边长分别为a和b的正方形拼在一起,B、C、G三点在同一直线上,连接BD和BF,若两正方形的边长满足a+b=10,ab=20,你能求出阴影部分的面积吗? 2·1·c·n·j·y
18、a,b,c为三角形ABC的三边,且满足a2+b2+c2+338=10a+24b+26c,试判别这个三角形的形状. 2-1-c-n-j-y
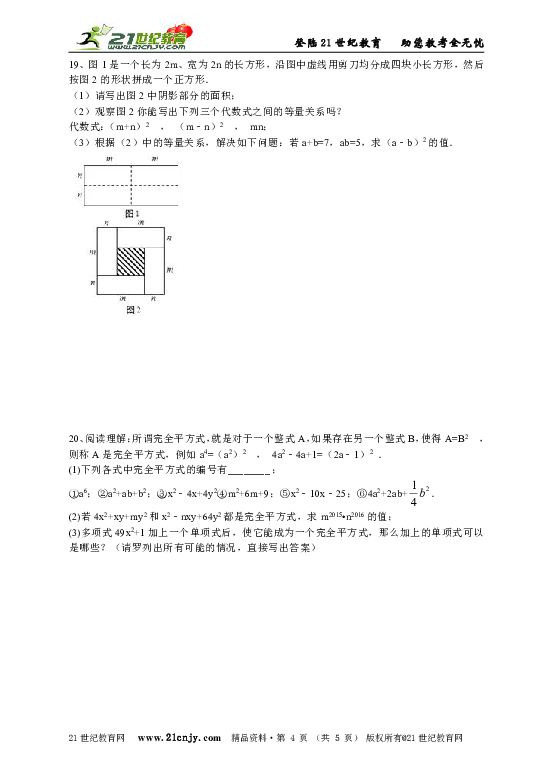
19、图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形. (1)请写出图2中阴影部分的面积; (2)观察图2你能写出下列三个代数式之间的等量关系吗? 代数式:(m+n)2 , (m﹣n)2 , mn; (3)根据(2)中的等量关系,解决如下问题:若a+b=7,ab=5,求(a﹣b)2的值. www.21-cn-jy.com
20、阅读理解:所谓完全平方式,就是对于一个整式A,如果存在另一个整式B,使得A=B2 , 则称A是完全平方式,例如a4=(a2)2 , 4a2﹣4a+1=(2a﹣1)2 .
(1)下列各式中完全平方式的编号有________?; ①a6;②a2+ab+b2;③x2﹣4x+4y2④m2+6m+9;⑤x2﹣10x﹣25;⑥4a2+2ab+.
(2)若4x2+xy+my2和x2﹣nxy+64y2都是完全平方式,求m2015?n2016的值;
(3)多项式49x2+1加上一个单项式后,使它能成为一个完全平方式,那么加上的单项式可以是哪些?(请罗列出所有可能的情况,直接写出答案) 21世纪教育网版权所有
答案解析
单选题
题号
1
2
3
4
5
6
7
8
答案
B
A
C
B
C
B
C
C
解析:
2、A 解:∵a+b=4,x+y=10, ∴a2+2ab+b2﹣x﹣y =(a+b)2﹣(x+y) =42﹣10 =6, 故选A. 3、C 解:∵a+b=3,ab=2, ∴a2+b2 =(a+b)2﹣2ab =32﹣2×2 =5, 故选C 4、B 解:∵a+ =3, ∴ , ∴ , ∴a2+ =7, 故选B. 5、C 解:∵(ax+3y)2=a2x2+6axy+9y2 , ∴a2x2+6axy+9y2=4x2﹣12xy+by2 , ∴6a=﹣12,b=9, 解得a=﹣2,b=9. 故选C. 6、B 解:∵x2﹣ax+36是一个完全平方式, ∴a=±12, 故选B 7、C 解:由题意可得,正方形的边长为(a+b), 故正方形的面积为(a+b)2 , 又∵原矩形的面积为4ab, ∴中间空的部分的面积=(a+b)2﹣4ab=(a﹣b)2 . 故选C. 8、C 解:根据“杨辉三角”规律得到(a+b)4的展开式中各项系数分别为1,4,6,4,1,即系数最大为6, 故选C 21教育网
二、填空题
9、3a2+6ab﹣18b2 解:原式=4a2﹣9b2﹣a2+6ab﹣9b2=3a2+6ab﹣18b2 . 故答案为:3a2+6ab﹣18b2 . 10、±20 解:根据题意得:△=m2﹣4×4×25=0, 解得:m=±20, 故答案是:±20. 11、3 解:∵a2﹣3ab+b2=0(a≠0,b≠0),∴a2+b2=3ab, ∴ + = = =3. 故答案为:3. 12、ab=0 解:∵(a+b)2=a2+2ab+b2 , ∴等式(a+b)2=a2+b2成立的条件为ab=0, 故答案为:ab=0. 13、﹣3ab 解:∵a2+ab+b2+M=(a﹣b)2=a2﹣2ab+b2 , ∴M=﹣3ab. 故答案为:﹣3ab. 14、6a+9 解:由题意得其面积增加的是(a+3)2﹣a2=6a+9. 故答案是:6a+9. 21cnjy.com
三、解答题
15、解:原式=4x2﹣4xy+y2﹣3x2+4xy﹣2y2=x2﹣y2 , 当x=,y=﹣2时,原式= ﹣4=﹣. 16、解:设原绿地的边长为xm, 则(x+3)2﹣x2=63, 解得;x=9, 答:原绿地的边长为9m 17、解(1)(a+b+c)2=a2+b2+c2+2ab+2bc+2ac (2)∵a+b=10,ab=20, ∴S阴影=a2+b2﹣(a+b)?b﹣a2=a2+b2﹣ab=(a+b)2﹣ab=×102﹣×20=50﹣30=20. 18、解:由a2+b2+c2+338=10a+24b+26c, 得:(a2﹣10a+25)+(b2﹣24b+144)+(c2﹣26c+169)=0, 即:(a﹣5)2+(b﹣12)2+(c﹣13)2=0, 由非负数的性质可得: , 解得 , ∵52+122=169=132 , 即a2+b2=c2 , ∴∠C=90°, 即三角形ABC为直角三角形. 19、解:(1)(m﹣n)2或(m+n)2﹣4mn; (2)(m﹣n)2=(m+n)2﹣4mn; (3)当a+b=7,ab=5时, (a﹣b)2 =(a+b)2﹣4ab =72﹣4×5 =49﹣20 =29. 20、(1)①④⑥21·cn·jy·com
(2)解:∵4x2+xy+my2和x2﹣mxy+64y2都是完全平方式, ∴m=,n=±16, 则原式=(×16)2015×16=16; (3)解:多项式49x2+1加上一个单项式后,使它能成为一个完全平方式,那么加上的单项式可以是14x,﹣14x,﹣1,﹣49x2 , .
同步练习
一、单选题
1、下列关系式中,正确的是(?? )
A、(a﹣b)2=a2﹣b2 B、(a+b)(a﹣b)=a2﹣b2 C、(a+b)2=a2+b2 D、(a+b)2=a2﹣2ab+b221·世纪*教育网
2、已知a+b=4,x+y=10,则a2+2ab+b2﹣x﹣y的值是(?? )
A、6 B、14 C、﹣6 D、4
3、已知a+b=3,ab=2,则a2+b2的值为(?? )
A、3 B、4 C、5 D、6
4、已知a+ =3,则a2+ 的值是(?? )
A、9 B、7 C、5 D、3
5、若(ax+3y)2=4x2﹣12xy+by2 ,则a,b的值分别为(?? )
A、2,9 B、2,﹣9 C、﹣2,9 D、﹣4,9
6、若关于x的二次三项式x2﹣ax+36是一个完全平方式,那么a的值是(?? )
A、12 B、±12 C、6 D、±6
7、如图(1),是一个长为2a宽为2b(a>b)的矩形,用剪刀沿矩形的两条对角轴剪开,把它分成四个全等的小矩形,然后按图(2)拼成一个新的正方形,则中间空白部分的面积是(?? )【来源:21·世纪·教育·网】
A、ab? B、(a+b)2? C、(a﹣b)2? D、a2﹣b2
8、我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”(如图所示)就是一例. 这个三角形的构造法则为:两腰上的数都是1,其余每个数均为其上方左右两数之和.事实上,这个三角形给出了(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应(a+b)2=a2+ab+b2展开式中各项的系数;第四行的四个数1,3,3,1,恰好对应着(a+b)3=a3+3a2b+3ab2+b3展开式中各项的系数等等.根据上面的规律,(a+b)4的展开式中各项系数最大的数为(?? )
A、4 B、5 C、6 D、7
二、填空题
9、计算题:(2a+3b)(2a﹣3b)﹣(a﹣3b)2=________?
10、若4x2+mxy+25y2是完全平方式,则m=________.
11、已知a2﹣3ab+b2=0(a≠0,b≠0),则代数式的值等于________.
12、等式(a+b)2=a2+b2成立的条件为________
13、若a2+ab+b2+M=(a﹣b)2 ,那么M=________.
14、已知正方形的边长为a,如果它的边长增加3,那么它的面积增加了________.
三、解答题
15、先化简,再求值:(2x﹣y)2+(6x3﹣8x2y+4xy2)÷(﹣2x),其中 ,y=﹣2.
16、某大学进行绿地改造,原有一正方形绿地,现将它每边都增加3m,则面积增加了63m2 . 问:原绿地的边长为多少? www-2-1-cnjy-com
17、把几个图形拼成一个新的图形,再通过图形面积的计算,常常可以得到一些有用的式子,或可以求出一些不规则图形的面积. (1)如图1,是将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形,试用不同的方法计算这个图形的面积,你能发现什么结论,请写出来. (2)如图2,是将两个边长分别为a和b的正方形拼在一起,B、C、G三点在同一直线上,连接BD和BF,若两正方形的边长满足a+b=10,ab=20,你能求出阴影部分的面积吗? 2·1·c·n·j·y
18、a,b,c为三角形ABC的三边,且满足a2+b2+c2+338=10a+24b+26c,试判别这个三角形的形状. 2-1-c-n-j-y
19、图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形. (1)请写出图2中阴影部分的面积; (2)观察图2你能写出下列三个代数式之间的等量关系吗? 代数式:(m+n)2 , (m﹣n)2 , mn; (3)根据(2)中的等量关系,解决如下问题:若a+b=7,ab=5,求(a﹣b)2的值. www.21-cn-jy.com
20、阅读理解:所谓完全平方式,就是对于一个整式A,如果存在另一个整式B,使得A=B2 , 则称A是完全平方式,例如a4=(a2)2 , 4a2﹣4a+1=(2a﹣1)2 .
(1)下列各式中完全平方式的编号有________?; ①a6;②a2+ab+b2;③x2﹣4x+4y2④m2+6m+9;⑤x2﹣10x﹣25;⑥4a2+2ab+.
(2)若4x2+xy+my2和x2﹣nxy+64y2都是完全平方式,求m2015?n2016的值;
(3)多项式49x2+1加上一个单项式后,使它能成为一个完全平方式,那么加上的单项式可以是哪些?(请罗列出所有可能的情况,直接写出答案) 21世纪教育网版权所有
答案解析
单选题
题号
1
2
3
4
5
6
7
8
答案
B
A
C
B
C
B
C
C
解析:
2、A 解:∵a+b=4,x+y=10, ∴a2+2ab+b2﹣x﹣y =(a+b)2﹣(x+y) =42﹣10 =6, 故选A. 3、C 解:∵a+b=3,ab=2, ∴a2+b2 =(a+b)2﹣2ab =32﹣2×2 =5, 故选C 4、B 解:∵a+ =3, ∴ , ∴ , ∴a2+ =7, 故选B. 5、C 解:∵(ax+3y)2=a2x2+6axy+9y2 , ∴a2x2+6axy+9y2=4x2﹣12xy+by2 , ∴6a=﹣12,b=9, 解得a=﹣2,b=9. 故选C. 6、B 解:∵x2﹣ax+36是一个完全平方式, ∴a=±12, 故选B 7、C 解:由题意可得,正方形的边长为(a+b), 故正方形的面积为(a+b)2 , 又∵原矩形的面积为4ab, ∴中间空的部分的面积=(a+b)2﹣4ab=(a﹣b)2 . 故选C. 8、C 解:根据“杨辉三角”规律得到(a+b)4的展开式中各项系数分别为1,4,6,4,1,即系数最大为6, 故选C 21教育网
二、填空题
9、3a2+6ab﹣18b2 解:原式=4a2﹣9b2﹣a2+6ab﹣9b2=3a2+6ab﹣18b2 . 故答案为:3a2+6ab﹣18b2 . 10、±20 解:根据题意得:△=m2﹣4×4×25=0, 解得:m=±20, 故答案是:±20. 11、3 解:∵a2﹣3ab+b2=0(a≠0,b≠0),∴a2+b2=3ab, ∴ + = = =3. 故答案为:3. 12、ab=0 解:∵(a+b)2=a2+2ab+b2 , ∴等式(a+b)2=a2+b2成立的条件为ab=0, 故答案为:ab=0. 13、﹣3ab 解:∵a2+ab+b2+M=(a﹣b)2=a2﹣2ab+b2 , ∴M=﹣3ab. 故答案为:﹣3ab. 14、6a+9 解:由题意得其面积增加的是(a+3)2﹣a2=6a+9. 故答案是:6a+9. 21cnjy.com
三、解答题
15、解:原式=4x2﹣4xy+y2﹣3x2+4xy﹣2y2=x2﹣y2 , 当x=,y=﹣2时,原式= ﹣4=﹣. 16、解:设原绿地的边长为xm, 则(x+3)2﹣x2=63, 解得;x=9, 答:原绿地的边长为9m 17、解(1)(a+b+c)2=a2+b2+c2+2ab+2bc+2ac (2)∵a+b=10,ab=20, ∴S阴影=a2+b2﹣(a+b)?b﹣a2=a2+b2﹣ab=(a+b)2﹣ab=×102﹣×20=50﹣30=20. 18、解:由a2+b2+c2+338=10a+24b+26c, 得:(a2﹣10a+25)+(b2﹣24b+144)+(c2﹣26c+169)=0, 即:(a﹣5)2+(b﹣12)2+(c﹣13)2=0, 由非负数的性质可得: , 解得 , ∵52+122=169=132 , 即a2+b2=c2 , ∴∠C=90°, 即三角形ABC为直角三角形. 19、解:(1)(m﹣n)2或(m+n)2﹣4mn; (2)(m﹣n)2=(m+n)2﹣4mn; (3)当a+b=7,ab=5时, (a﹣b)2 =(a+b)2﹣4ab =72﹣4×5 =49﹣20 =29. 20、(1)①④⑥21·cn·jy·com
(2)解:∵4x2+xy+my2和x2﹣mxy+64y2都是完全平方式, ∴m=,n=±16, 则原式=(×16)2015×16=16; (3)解:多项式49x2+1加上一个单项式后,使它能成为一个完全平方式,那么加上的单项式可以是14x,﹣14x,﹣1,﹣49x2 , .
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
