第1章 数列章末复习提升
图片预览




文档简介
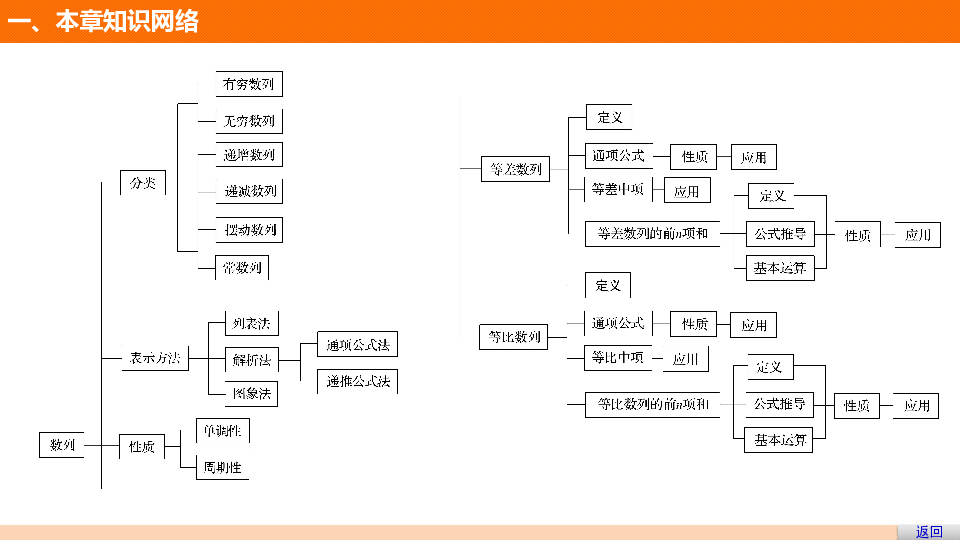
课件38张PPT。第一章 数 列章末复习提升一、本章知识网络二、知识要点归纳三、题型探究栏目索引四、思想方法总结一、本章知识网络返回 二、知识要点归纳1.求数列的通项
(1)数列前n项和Sn与通项an的关系:(2)当已知数列{an}中,满足an+1-an=f(n),且f(1)+f(2)+…+f(n)可求,则可用累加法求数列的通项an,常利用恒等式an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)(n≥2).(4)作新数列法:对由递推公式给出的数列,经过变形后化归成等差数列或等比数列来求通项.
(5)归纳、猜想、证明法.2.等差、等比数列的性质23.求数列的前n项和的基本方法
(1)公式法:利用等差数列或等比数列前n项和Sn公式;
(2)分组求和:把一个数列分成几个可以直接求和的数列;
(3)裂项(相消)法:有时把一个数列的通项公式分成两项差的形式,相加过程消去中间项,只剩有限项再求和;
(4)错位相减:适用于一个等差数列和一个等比数列对应项相乘构成的数列求和;
(5)倒序相加:例如等差数列前n项和公式的推导;
(6)并项求和法:适用于正负相间的数列.返回 三、题型探究题型一 数列的实际应用
例1 甲、乙两人连续6年对某县农村养鸡业规模进行调查,提供两个不同的信息图如图所示.甲调查表明:从第1年每个养鸡场出产1万只鸡上升到第6年平均每个鸡场出产2万只鸡,乙调查表明:由第1年养鸡场个数30个减少到第6年10个.请你根据提供的信息说明,求:
(1)第2年养鸡场的个数及全县出产鸡的总只数;解析答案解 由题干图可知,从第1年到第6年平均每个养鸡场出产的鸡只数成等差数列,记为数列{an},公差为d1,且a1=1,a6=2;从第1年到第6年的养鸡场个数也成等差数列,记为数列{bn},公差为d2,且b1=30,b6=10;从第1年到第6年全县出产鸡的总只数记为数列{cn},则cn=anbn.解析答案c2=a2b2=1.2×26=31.2.
所以第2年养鸡场的个数为26个,全县出产鸡的总只数是31.2万只.(2)到第6年这个县的养鸡业比第1年是扩大了还是缩小了?请说明理由;解 c6=a6b6=2×10=20所以到第6年这个县的养鸡业比第1年缩小了.解析答案(3)哪一年的规模最大?请说明理由.解 ∵an=1+(n-1)×0.2=0.2n+0.8,
bn=30+(n-1)×(-4)=-4n+34(1≤n≤6),
∴cn=anbn=(0.2n+0.8)(-4n+34)
=-0.8n2+3.6n+27.2(1≤n≤6).解析答案反思与感悟所以第2年的规模最大.解决与数列有关的应用题应注意以下几点:
(1)题目中用到的数列是等差数列还是等比数列.
(2)题目中要求的是数列的项还是和.
(3)所用的数列的首项是哪个?
(4)得出的结论是否符合实际.反思与感悟跟踪训练1 某企业的资金每一年都比上一年分红后的资金增加一倍,并且每年年底固定给股东们分红500万元.该企业2014年年底分红后的资金为1 000万元.
(1)求该企业2018年年底分红后的资金;解析答案解 设an为(2014+n)年年底分红后的资金,其中n∈N*,
则a1=2×1 000-500=1 500,
a2=2×1 500-500=2 500,
…,
an=2an-1-500(n≥2).
所以an-500=2(an-1-500)(n≥2),
即数列{an-500}是首项为a1-500=1 000,公比为2的等比数列.
所以an-500=1 000×2n-1,
所以an=1 000×2n-1+500.
a4=1 000×24-1+500=8 500,
所以该企业2018年年底分红后的资金为8 500万元.(2)求该企业从哪一年开始年底分红后的资金超过32 500万元.解 由an>32 500,即2n-1>32,得n>6,
所以该企业从2021年开始年底分红后的资金超过32 500万元.解析答案解析答案(1)求数列{an}的通项公式;解析答案∴a1=2λ-1.解析答案反思与感悟∵n∈N*,∴n=2 002,
故当n=2 002时,bn最大.反思与感悟反思与感悟数列是高中代数的重点内容之一,它始终处在知识的交汇点上,如数列与函数、方程、不等式等其他知识有较多交汇处.它包涵知识点多、思想丰富、综合性强,已成为近年高考的一大亮点.跟踪训练2 已知二次函数f(x)=x2-ax+a(x∈R)同时满足:①不等式f(x)≤0的解集有且只有一个元素;②在定义域内存在0<x1<x2,使得不等式f(x1)>f(x2)成立.设数列{an}的前n项和Sn=f(n).
(1)求f(x)的表达式;解析答案解 ∵f(x)≤0的解集有且只有一个元素,
∴Δ=a2-4a=0,∴a=0或a=4.
当a=4时,函数f(x)=x2-4x+4在(0,2)上递减,故存在0<x1<x2,使f(x1)>f(x2)成立;
而当a=0时,f(x)=x2在(0+∞)上递增,不合题意.
故a=4,f(x)=x2-4x+4.(2)求数列{an}的表达式.解 由(1)知,Sn=n2-4n+4.
当n≥2时,an=Sn-Sn-1
=(n2-4n+4)-[(n-1)2-4(n-1)+4]=2n-5,
当n=1时,a1=S1=1不适合上式,解析答案返回1.转化与化归思想求数列通项
由递推公式求通项公式,要求掌握的方法有两种,一种求法是先找出数列的前几项,通过观察、归纳得出,然后证明;另一种是通过变形转化为等差数列或等比数列,再采用公式求出. 四、思想方法总结例1 已知数列{an}满足an+1=2an+3×2n,a1=2,求数列{an}的通项公式.解 an+1=2an+3×2n两边除以2n+1,得解析答案跟踪训练1 已知数列{an}满足an+1=2an+3·5n,a1=6,求数列{an}的通项公式.解析答案解 设an+1+x·5n+1=2(an+x·5n) ①
将an+1=2an+3·5n代入①式,
得2an+3·5n+x·5n+1=2an+2x·5n,
等式两边消去2an,得3·5n+x·5n+1=2x·5n,
两边除以5n,得3+5x=2x,则x=-1,
代入①式得an+1-5n+1=2(an-5n) ②
由a1-51=6-5=1≠0及②式得,∴{an-5n}是以1为首项,2为公比的等比数列,
∴an-5n=1×2n-1=2n-1,
∴an=2n-1+5n(n∈N*).2.方程思想
在等差数列和等比数列中,通项公式an和前n项和公式Sn共涉及五个量:a1,an,n,d(q),Sn,其中首项a1和公差
d(公比q)为基本量,“知三求二”是指将已知条件转换成关于a1,an,n,d(q),Sn的方程组,通过方程的思想解出需要的量.例2 等差数列{an}各项均为正整数,a1=3,前n项和为Sn,等比数列{bn}中,b1=1且b2S2=64,{ban}是公比为64的等比数列,求{an},{bn}的通项公式.解析答案解 设{an}的公差为d,{bn}的公比为q,则d为正整数,an=3+(n-1)d,bn=qn-1.故an=2n+1,bn=8n-1.解析答案解 设数列{an}的公差为d,由题意得1.等差数列与等比数列是高中阶段学习的两种最基本的数列,也是高考中经常考查并且重点考查的内容之一,这类问题多从数列的本质入手,考查这两种基本数列的概念、基本性质、简单运算、通项公式、求和公式等问题.
2.数列求和的方法:一般的数列求和,应从通项入手,若无通项,先求通项,然后通过对通项变形,转化为与特殊数列有关或具备某种方法适用特点的形式,从而选择合适的方法求和.返回课堂小结本课结束更多精彩内容请登录:www.91taoke.com
(1)数列前n项和Sn与通项an的关系:(2)当已知数列{an}中,满足an+1-an=f(n),且f(1)+f(2)+…+f(n)可求,则可用累加法求数列的通项an,常利用恒等式an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)(n≥2).(4)作新数列法:对由递推公式给出的数列,经过变形后化归成等差数列或等比数列来求通项.
(5)归纳、猜想、证明法.2.等差、等比数列的性质23.求数列的前n项和的基本方法
(1)公式法:利用等差数列或等比数列前n项和Sn公式;
(2)分组求和:把一个数列分成几个可以直接求和的数列;
(3)裂项(相消)法:有时把一个数列的通项公式分成两项差的形式,相加过程消去中间项,只剩有限项再求和;
(4)错位相减:适用于一个等差数列和一个等比数列对应项相乘构成的数列求和;
(5)倒序相加:例如等差数列前n项和公式的推导;
(6)并项求和法:适用于正负相间的数列.返回 三、题型探究题型一 数列的实际应用
例1 甲、乙两人连续6年对某县农村养鸡业规模进行调查,提供两个不同的信息图如图所示.甲调查表明:从第1年每个养鸡场出产1万只鸡上升到第6年平均每个鸡场出产2万只鸡,乙调查表明:由第1年养鸡场个数30个减少到第6年10个.请你根据提供的信息说明,求:
(1)第2年养鸡场的个数及全县出产鸡的总只数;解析答案解 由题干图可知,从第1年到第6年平均每个养鸡场出产的鸡只数成等差数列,记为数列{an},公差为d1,且a1=1,a6=2;从第1年到第6年的养鸡场个数也成等差数列,记为数列{bn},公差为d2,且b1=30,b6=10;从第1年到第6年全县出产鸡的总只数记为数列{cn},则cn=anbn.解析答案c2=a2b2=1.2×26=31.2.
所以第2年养鸡场的个数为26个,全县出产鸡的总只数是31.2万只.(2)到第6年这个县的养鸡业比第1年是扩大了还是缩小了?请说明理由;解 c6=a6b6=2×10=20
bn=30+(n-1)×(-4)=-4n+34(1≤n≤6),
∴cn=anbn=(0.2n+0.8)(-4n+34)
=-0.8n2+3.6n+27.2(1≤n≤6).解析答案反思与感悟所以第2年的规模最大.解决与数列有关的应用题应注意以下几点:
(1)题目中用到的数列是等差数列还是等比数列.
(2)题目中要求的是数列的项还是和.
(3)所用的数列的首项是哪个?
(4)得出的结论是否符合实际.反思与感悟跟踪训练1 某企业的资金每一年都比上一年分红后的资金增加一倍,并且每年年底固定给股东们分红500万元.该企业2014年年底分红后的资金为1 000万元.
(1)求该企业2018年年底分红后的资金;解析答案解 设an为(2014+n)年年底分红后的资金,其中n∈N*,
则a1=2×1 000-500=1 500,
a2=2×1 500-500=2 500,
…,
an=2an-1-500(n≥2).
所以an-500=2(an-1-500)(n≥2),
即数列{an-500}是首项为a1-500=1 000,公比为2的等比数列.
所以an-500=1 000×2n-1,
所以an=1 000×2n-1+500.
a4=1 000×24-1+500=8 500,
所以该企业2018年年底分红后的资金为8 500万元.(2)求该企业从哪一年开始年底分红后的资金超过32 500万元.解 由an>32 500,即2n-1>32,得n>6,
所以该企业从2021年开始年底分红后的资金超过32 500万元.解析答案解析答案(1)求数列{an}的通项公式;解析答案∴a1=2λ-1.解析答案反思与感悟∵n∈N*,∴n=2 002,
故当n=2 002时,bn最大.反思与感悟反思与感悟数列是高中代数的重点内容之一,它始终处在知识的交汇点上,如数列与函数、方程、不等式等其他知识有较多交汇处.它包涵知识点多、思想丰富、综合性强,已成为近年高考的一大亮点.跟踪训练2 已知二次函数f(x)=x2-ax+a(x∈R)同时满足:①不等式f(x)≤0的解集有且只有一个元素;②在定义域内存在0<x1<x2,使得不等式f(x1)>f(x2)成立.设数列{an}的前n项和Sn=f(n).
(1)求f(x)的表达式;解析答案解 ∵f(x)≤0的解集有且只有一个元素,
∴Δ=a2-4a=0,∴a=0或a=4.
当a=4时,函数f(x)=x2-4x+4在(0,2)上递减,故存在0<x1<x2,使f(x1)>f(x2)成立;
而当a=0时,f(x)=x2在(0+∞)上递增,不合题意.
故a=4,f(x)=x2-4x+4.(2)求数列{an}的表达式.解 由(1)知,Sn=n2-4n+4.
当n≥2时,an=Sn-Sn-1
=(n2-4n+4)-[(n-1)2-4(n-1)+4]=2n-5,
当n=1时,a1=S1=1不适合上式,解析答案返回1.转化与化归思想求数列通项
由递推公式求通项公式,要求掌握的方法有两种,一种求法是先找出数列的前几项,通过观察、归纳得出,然后证明;另一种是通过变形转化为等差数列或等比数列,再采用公式求出. 四、思想方法总结例1 已知数列{an}满足an+1=2an+3×2n,a1=2,求数列{an}的通项公式.解 an+1=2an+3×2n两边除以2n+1,得解析答案跟踪训练1 已知数列{an}满足an+1=2an+3·5n,a1=6,求数列{an}的通项公式.解析答案解 设an+1+x·5n+1=2(an+x·5n) ①
将an+1=2an+3·5n代入①式,
得2an+3·5n+x·5n+1=2an+2x·5n,
等式两边消去2an,得3·5n+x·5n+1=2x·5n,
两边除以5n,得3+5x=2x,则x=-1,
代入①式得an+1-5n+1=2(an-5n) ②
由a1-51=6-5=1≠0及②式得,∴{an-5n}是以1为首项,2为公比的等比数列,
∴an-5n=1×2n-1=2n-1,
∴an=2n-1+5n(n∈N*).2.方程思想
在等差数列和等比数列中,通项公式an和前n项和公式Sn共涉及五个量:a1,an,n,d(q),Sn,其中首项a1和公差
d(公比q)为基本量,“知三求二”是指将已知条件转换成关于a1,an,n,d(q),Sn的方程组,通过方程的思想解出需要的量.例2 等差数列{an}各项均为正整数,a1=3,前n项和为Sn,等比数列{bn}中,b1=1且b2S2=64,{ban}是公比为64的等比数列,求{an},{bn}的通项公式.解析答案解 设{an}的公差为d,{bn}的公比为q,则d为正整数,an=3+(n-1)d,bn=qn-1.故an=2n+1,bn=8n-1.解析答案解 设数列{an}的公差为d,由题意得1.等差数列与等比数列是高中阶段学习的两种最基本的数列,也是高考中经常考查并且重点考查的内容之一,这类问题多从数列的本质入手,考查这两种基本数列的概念、基本性质、简单运算、通项公式、求和公式等问题.
2.数列求和的方法:一般的数列求和,应从通项入手,若无通项,先求通项,然后通过对通项变形,转化为与特殊数列有关或具备某种方法适用特点的形式,从而选择合适的方法求和.返回课堂小结本课结束更多精彩内容请登录:www.91taoke.com
