江西省宜春中学2017届高三3月月考数学(理)试题
文档属性
| 名称 | 江西省宜春中学2017届高三3月月考数学(理)试题 |
|
|
| 格式 | zip | ||
| 文件大小 | 272.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-20 00:00:00 | ||
图片预览




文档简介
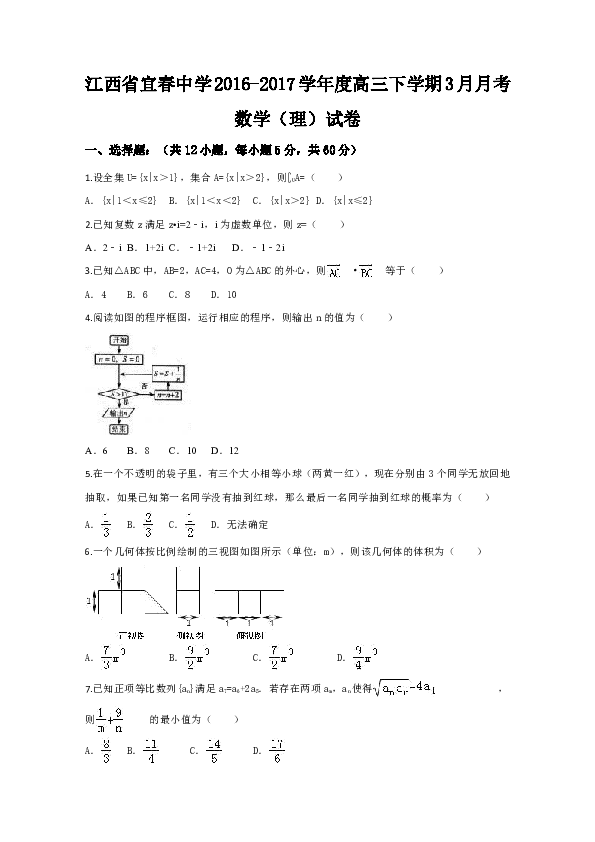
江西省宜春中学2016-2017学年度高三下学期3月月考数学(理)试卷
一、选择题:(共12小题,每小题5分,共60分)
1.设全集U={x|x>1},集合A={x|x>2},则 UA=( )
A.{x|1<x≤2}
B.{x|1<x<2}
C.{x|x>2}
D.{x|x≤2}
2.已知复数z满足z i=2﹣i,i为虚数单位,则z=( )
A.2﹣i
B.1+2i
C.﹣1+2i
D.﹣1﹣2i
3.已知△ABC中,AB=2,AC=4,O为△ABC的外心,则 等于( )
A.4
B.6
C.8
D.10
4.阅读如图的程序框图,运行相应的程序,则输出n的值为( )
( http: / / www.21cnjy.com )
A.6
B.8
C.10
D.12
5.在一个不透明的袋子里,有三个大小相等
( http: / / www.21cnjy.com )小球(两黄一红),现在分别由3个同学无放回地抽取,如果已知第一名同学没有抽到红球,那么最后一名同学抽到红球的概率为( )
A.
B.
C.
D.无法确定
6.一个几何体按比例绘制的三视图如图所示(单位:m),则该几何体的体积为( )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
A.
B.
C.
D.
7.已知正项等比数列{an}满足a7=a6+2a5.若存在两项am,an使得,则的最小值为( )
A.
B.
C.
D.
8.将函数y=sin(x+)cos(x+)的图象沿x轴向右平移个单位后,得到一个偶函数的图象,则φ的取值不可能是( )
A.
B.﹣
C.
D.
9.设m,n是两条不同的直线,α,β是两个不同的平面,下列命题是真命题的是( )
A.若m∥α,m∥β,则α∥β
B.若m∥α,α∥β,则m∥β
C.若,,则
D.若,,则
10.已知椭圆的焦点是F1(0,﹣),F2(0,),离心率e=,若点P在椭圆上,且=,则∠F1PF2的大小为( )
A.
B.
C.
D.
11.设函数f(x)=xsinx+cosx的图象在点(t,f(t))处切线的斜率为k,则函数k=g(t)的图象大致为( )
A.
( http: / / www.21cnjy.com )
B.
( http: / / www.21cnjy.com )
C.
( http: / / www.21cnjy.com )
D.
( http: / / www.21cnjy.com )
12.若圆x2+y2﹣4x﹣4y﹣10=0上至少有三个不同点到直线l:x﹣y+b=0的距离为,则b的取值范围是( )
A.[﹣2,2]
B.[﹣10,10]
C.(﹣∞,﹣10]∪[10,+∞)
D.(﹣∞,﹣2]∪[2,+∞)
二、填空题:(本大题共4小题,每小题5分,共20分)
13.已知向量,的夹角为,且|=1,,
|=
.
14.(x﹣)4(x﹣2)的展开式中,x2的系数为
.
15.已知等比数列{an}的各项均为正数,且满足:a1a7=4,则数列{log2an}的前7项之和为
.
16.设定义域为的函数,若关于的方程有三个不同的实数解,则____
三、解答题:(本题共6小题,共70分,解答过程应写出文字说明,证明过程或演算步骤)
17.在△ABC中,角A,B,C的对边分别为a,b,c,已知bcos2+acos2=c.
(Ⅰ)求证:a,c,b成等差数列;
(Ⅱ)若C=,△ABC的面积为2,求c.
18.如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,AB⊥AD,AB∥CD,CD=AD=2AB=2AP.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
(1)求证:平面PCD⊥平面PAD;
(2)在侧棱PC上是否存在点E,使得BE∥平面PAD,若存在,确定点E位置;若不存在,说明理由.
19.甲、乙、丙三人按下面的规则进行乒乓球比赛:第一局由甲、乙参加而丙轮空,以后每一局由前一局的获胜者与轮空者进行比赛,而前一局的失败者轮空.比赛按这种规则一直进行到其中一人连胜两局或打满6局时停止.设在每局中参赛者胜负的概率均为,且各局胜负相互独立.求:
(1)打满4局比赛还未停止的概率;
(2)比赛停止时已打局数ξ的分布列与期望E(ξ).
令Ak,Bk,Ck分别表示甲、乙、丙在第k局中获胜.
20.如图,射线OA,OB所在的直线的方向向量分别为,,点P在∠AOB内,PM⊥OA于M,PN⊥OB于N;
(1)若k=1,,求|OM|的值;
(2)若P(2,1),△OMP的面积为,求k的值;
(3)已知k为常数,M,N的中点为T,且S△MON=,当P变化时,求动点T轨迹方程.
( http: / / www.21cnjy.com )
21.已知函数f(x)=ax3﹣bex(a∈R,b∈R),且f(x)在x=0处的切线与x﹣y+3=0垂直.
(1)若函数f(x)在[,1]存在单调递增区间,求实数a的取值范围;
(2)若f′(x)有两个极值点x1,x2,且x1<x2,求a的取值范围;
(3)在第二问的前提下,证明:﹣<f′(x1)<﹣1.
22.选修4-1几何证明选讲如图,正方形A
( http: / / www.21cnjy.com )BCD边长为2,以D为圆心、DA为半径的圆弧与以BC为直径的半圆O交于点F,连结CF并延长交AB于点E.
(1)求证:AE=EB;
(2)求EFFC的值.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
23.
[选修4-4:坐标系与参数方程](共1小题,满分10分)
在直角坐标系xOy中,曲线C1的参数方程为(其中α为参数),以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4sinθ.
(Ⅰ)若A,B为曲线C1,C2的公共点,求直线AB的斜率;
(Ⅱ)若A,B分别为曲线C1,C2上的动点,当|AB|取最大值时,求△AOB的面积.
24.选修4-5不等式选讲
已知函数f(x)=|x﹣|﹣|2x+1|.
(Ⅰ)求f(x)的值域;
(Ⅱ)若f(x)的最大值时a,已知x,y,z均为正实数,且x+y+z=a,求证:
++≥1.
参考答案
1
2
3
4
5
6
7
8
9
10
11
12
A
D
B
B
C
C
B
C
C
D
A
A
13.3
14.16
15.7
16.11
17.解:(Ⅰ)证明:由正弦定理得:
即,
∴sinB+sinA+sinBcosA+cosBsinA=3sinC…
∴sinB+sinA+sin(A+B)=3sinC
∴sinB+sinA+sinC=3sinC…
∴sinB+sinA=2sinC
∴a+b=2c…
∴a,c,b成等差数列.…
(Ⅱ)
∴ab=8…
c2=a2+b2﹣2abcosC
=a2+b2﹣ab
=(a+b)2﹣3ab
=4c2﹣24.…
∴c2=8得…
18.【解答】(1)证明:∵PA⊥平面ABCD
∴PA⊥CD
①
又∵AB⊥AD,AB∥CD,
∴CD⊥AD
②
由①②可得
CD⊥平面PAD
又CD 平面PCD
∴平面PCD⊥平面PAD
(2)解:当点E是PC的中点时,BE∥平面PAD.
证明如下:设PD的中点为F,连接EF,AF
易得EF是△PCD的中位线
∴EF∥CD,EF=CD
由题设可得
AB∥CD,AF=CD
∴EF∥AB,EF=AB
∴四边形ABEF为平行四边形
∴BE∥AF
又BE 平面PAD,AF 平面PAD
∴BE∥平面PAD
19.
(1)由独立事件同时发生与互斥事件至少有一个发生的概率公式知,打满4局比赛还未停止
( http: / / www.21cnjy.com )
20.解:(1)因为,所以|OP|=,
因为OA的方程为y=x,即x﹣y=0,点P到直线的距离为=,
所以|OM|==;
(2)直线OA的方程为kx﹣y=0,P(2,1)到直线的距离为d=,
所以|OM|=,
所以△OMP的面积为××=,
所以;
(3)设M(x1,kx1),N(x2,﹣kx2),T(x,y),x1>0,x2>0,k>0,
设直线OA的倾斜角为α,则,
根据题意得
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
代入
化简得动点T轨迹方程为.
21.解:因为f'(x)=ax2﹣bex,所以f'(0)=﹣b=﹣1,所以b=1…
(1)由前可知,f'(x)=ax2﹣ex
根据题意:f'(x)>0在上有解,即ax2﹣ex>0在上有解
…
即在上有解,令,故只需
所以,所以,当时,g'(x)<0,所以g(x)在上单调递减,
所以g(x)min=g(1)=e,所以
a>e…
(2)令h(x)=f'(x),则h(x)=ax2﹣ex,所以h'(x)=2ax﹣ex
由题可知,h'(x)=0有两个根x1,x2,即2ax﹣ex=0有两个根x1,x2,
又x=0显然不是该方程的根,所以方程有两个根,…
设φ(x)=,则φ′(x)=,当x<0时,φ'(x)<0,φ(x)单调递减;
当0<x<1时,φ′(x)<0,φ(x)单调递减;当x>1时,φ′(x)>0,φ(x)单调递增.
故要使方程2a=有两个根,只需2a>φ(1)=e,即a>,
所以a的取值范围是(,+∞),
(3)由(2)得:0<x1<1<x2…
且由h'(x1)=0,得2ax1﹣=0,所以a=,x1∈(0,1)…
所以f′(x1)=h(x1)=a﹣=(﹣1),x1∈(0,1),
令r(t)=et(﹣1),(0<t<1),则r′(t)=et()<0,
r(t)在(0,1)上单调递减,
所以r(1)<r(t)<r(0),即﹣<f′(x1)<﹣1.…
22.【解答】(1)证明:由以D为圆心DA为半径作圆,
而ABCD为正方形,∴EA为圆D的切线
依据切割线定理,得EA2=EFEC…
另外圆O以BC为直径,∴EB是圆O的切线,
同样依据切割线定理得EB2=EFEC…
故AE=EB…
(2)解:连结BF,∵BC为圆O直径,
∴BF⊥EC
在RT△EBC中,有…
又在Rt△BCE中,
由射影定理得EFFC=BF2=.…
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
23.解:(Ⅰ)消去参数α得曲线C1的普通方程C1:x2+y2﹣2x=0.…(1)
将曲线C2:ρ=4sinθ化为直角坐标方程得x2+y2﹣4y=0.…(2)
由(1)﹣(2)得4y﹣2x=0,即为直线AB的方程,故直线AB的斜率为;
(Ⅱ)由C1:(x﹣1)2+y2=1知曲线C1是以C1(1,0)为圆心,半径为1的圆,
由C2:x2+(y﹣2)2=4知曲线C2:是以C2(0,2)为圆心,半径为2的圆.
∵|AB|≤|AC1|+|C1C2|+|BC2|,
∴当|AB|取最大值时,圆心C1,C2在直线AB上,
∴直线AB(即直线C1C2)的方程为:2x+y=2.
∵O到直线AB的距离为,
又此时|AB|=|C1C2|+1+2=3+,
∴△AOB的面积为.
24.(Ⅰ)解:函数f(x)=|x﹣|﹣|2x+1|=
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com ),
函数的图象如图所示,则函数的值域为(﹣∞,1];
( http: / / www.21cnjy.com )
(Ⅱ)证明:由题意x,y,z均为正实数,x+y+z=1,
由柯西不等式可得(x+y+z)(++)≥(y+z+z)2=1,
∴++≥1.
一、选择题:(共12小题,每小题5分,共60分)
1.设全集U={x|x>1},集合A={x|x>2},则 UA=( )
A.{x|1<x≤2}
B.{x|1<x<2}
C.{x|x>2}
D.{x|x≤2}
2.已知复数z满足z i=2﹣i,i为虚数单位,则z=( )
A.2﹣i
B.1+2i
C.﹣1+2i
D.﹣1﹣2i
3.已知△ABC中,AB=2,AC=4,O为△ABC的外心,则 等于( )
A.4
B.6
C.8
D.10
4.阅读如图的程序框图,运行相应的程序,则输出n的值为( )
( http: / / www.21cnjy.com )
A.6
B.8
C.10
D.12
5.在一个不透明的袋子里,有三个大小相等
( http: / / www.21cnjy.com )小球(两黄一红),现在分别由3个同学无放回地抽取,如果已知第一名同学没有抽到红球,那么最后一名同学抽到红球的概率为( )
A.
B.
C.
D.无法确定
6.一个几何体按比例绘制的三视图如图所示(单位:m),则该几何体的体积为( )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
A.
B.
C.
D.
7.已知正项等比数列{an}满足a7=a6+2a5.若存在两项am,an使得,则的最小值为( )
A.
B.
C.
D.
8.将函数y=sin(x+)cos(x+)的图象沿x轴向右平移个单位后,得到一个偶函数的图象,则φ的取值不可能是( )
A.
B.﹣
C.
D.
9.设m,n是两条不同的直线,α,β是两个不同的平面,下列命题是真命题的是( )
A.若m∥α,m∥β,则α∥β
B.若m∥α,α∥β,则m∥β
C.若,,则
D.若,,则
10.已知椭圆的焦点是F1(0,﹣),F2(0,),离心率e=,若点P在椭圆上,且=,则∠F1PF2的大小为( )
A.
B.
C.
D.
11.设函数f(x)=xsinx+cosx的图象在点(t,f(t))处切线的斜率为k,则函数k=g(t)的图象大致为( )
A.
( http: / / www.21cnjy.com )
B.
( http: / / www.21cnjy.com )
C.
( http: / / www.21cnjy.com )
D.
( http: / / www.21cnjy.com )
12.若圆x2+y2﹣4x﹣4y﹣10=0上至少有三个不同点到直线l:x﹣y+b=0的距离为,则b的取值范围是( )
A.[﹣2,2]
B.[﹣10,10]
C.(﹣∞,﹣10]∪[10,+∞)
D.(﹣∞,﹣2]∪[2,+∞)
二、填空题:(本大题共4小题,每小题5分,共20分)
13.已知向量,的夹角为,且|=1,,
|=
.
14.(x﹣)4(x﹣2)的展开式中,x2的系数为
.
15.已知等比数列{an}的各项均为正数,且满足:a1a7=4,则数列{log2an}的前7项之和为
.
16.设定义域为的函数,若关于的方程有三个不同的实数解,则____
三、解答题:(本题共6小题,共70分,解答过程应写出文字说明,证明过程或演算步骤)
17.在△ABC中,角A,B,C的对边分别为a,b,c,已知bcos2+acos2=c.
(Ⅰ)求证:a,c,b成等差数列;
(Ⅱ)若C=,△ABC的面积为2,求c.
18.如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,AB⊥AD,AB∥CD,CD=AD=2AB=2AP.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
(1)求证:平面PCD⊥平面PAD;
(2)在侧棱PC上是否存在点E,使得BE∥平面PAD,若存在,确定点E位置;若不存在,说明理由.
19.甲、乙、丙三人按下面的规则进行乒乓球比赛:第一局由甲、乙参加而丙轮空,以后每一局由前一局的获胜者与轮空者进行比赛,而前一局的失败者轮空.比赛按这种规则一直进行到其中一人连胜两局或打满6局时停止.设在每局中参赛者胜负的概率均为,且各局胜负相互独立.求:
(1)打满4局比赛还未停止的概率;
(2)比赛停止时已打局数ξ的分布列与期望E(ξ).
令Ak,Bk,Ck分别表示甲、乙、丙在第k局中获胜.
20.如图,射线OA,OB所在的直线的方向向量分别为,,点P在∠AOB内,PM⊥OA于M,PN⊥OB于N;
(1)若k=1,,求|OM|的值;
(2)若P(2,1),△OMP的面积为,求k的值;
(3)已知k为常数,M,N的中点为T,且S△MON=,当P变化时,求动点T轨迹方程.
( http: / / www.21cnjy.com )
21.已知函数f(x)=ax3﹣bex(a∈R,b∈R),且f(x)在x=0处的切线与x﹣y+3=0垂直.
(1)若函数f(x)在[,1]存在单调递增区间,求实数a的取值范围;
(2)若f′(x)有两个极值点x1,x2,且x1<x2,求a的取值范围;
(3)在第二问的前提下,证明:﹣<f′(x1)<﹣1.
22.选修4-1几何证明选讲如图,正方形A
( http: / / www.21cnjy.com )BCD边长为2,以D为圆心、DA为半径的圆弧与以BC为直径的半圆O交于点F,连结CF并延长交AB于点E.
(1)求证:AE=EB;
(2)求EFFC的值.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
23.
[选修4-4:坐标系与参数方程](共1小题,满分10分)
在直角坐标系xOy中,曲线C1的参数方程为(其中α为参数),以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4sinθ.
(Ⅰ)若A,B为曲线C1,C2的公共点,求直线AB的斜率;
(Ⅱ)若A,B分别为曲线C1,C2上的动点,当|AB|取最大值时,求△AOB的面积.
24.选修4-5不等式选讲
已知函数f(x)=|x﹣|﹣|2x+1|.
(Ⅰ)求f(x)的值域;
(Ⅱ)若f(x)的最大值时a,已知x,y,z均为正实数,且x+y+z=a,求证:
++≥1.
参考答案
1
2
3
4
5
6
7
8
9
10
11
12
A
D
B
B
C
C
B
C
C
D
A
A
13.3
14.16
15.7
16.11
17.解:(Ⅰ)证明:由正弦定理得:
即,
∴sinB+sinA+sinBcosA+cosBsinA=3sinC…
∴sinB+sinA+sin(A+B)=3sinC
∴sinB+sinA+sinC=3sinC…
∴sinB+sinA=2sinC
∴a+b=2c…
∴a,c,b成等差数列.…
(Ⅱ)
∴ab=8…
c2=a2+b2﹣2abcosC
=a2+b2﹣ab
=(a+b)2﹣3ab
=4c2﹣24.…
∴c2=8得…
18.【解答】(1)证明:∵PA⊥平面ABCD
∴PA⊥CD
①
又∵AB⊥AD,AB∥CD,
∴CD⊥AD
②
由①②可得
CD⊥平面PAD
又CD 平面PCD
∴平面PCD⊥平面PAD
(2)解:当点E是PC的中点时,BE∥平面PAD.
证明如下:设PD的中点为F,连接EF,AF
易得EF是△PCD的中位线
∴EF∥CD,EF=CD
由题设可得
AB∥CD,AF=CD
∴EF∥AB,EF=AB
∴四边形ABEF为平行四边形
∴BE∥AF
又BE 平面PAD,AF 平面PAD
∴BE∥平面PAD
19.
(1)由独立事件同时发生与互斥事件至少有一个发生的概率公式知,打满4局比赛还未停止
( http: / / www.21cnjy.com )
20.解:(1)因为,所以|OP|=,
因为OA的方程为y=x,即x﹣y=0,点P到直线的距离为=,
所以|OM|==;
(2)直线OA的方程为kx﹣y=0,P(2,1)到直线的距离为d=,
所以|OM|=,
所以△OMP的面积为××=,
所以;
(3)设M(x1,kx1),N(x2,﹣kx2),T(x,y),x1>0,x2>0,k>0,
设直线OA的倾斜角为α,则,
根据题意得
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
代入
化简得动点T轨迹方程为.
21.解:因为f'(x)=ax2﹣bex,所以f'(0)=﹣b=﹣1,所以b=1…
(1)由前可知,f'(x)=ax2﹣ex
根据题意:f'(x)>0在上有解,即ax2﹣ex>0在上有解
…
即在上有解,令,故只需
所以,所以,当时,g'(x)<0,所以g(x)在上单调递减,
所以g(x)min=g(1)=e,所以
a>e…
(2)令h(x)=f'(x),则h(x)=ax2﹣ex,所以h'(x)=2ax﹣ex
由题可知,h'(x)=0有两个根x1,x2,即2ax﹣ex=0有两个根x1,x2,
又x=0显然不是该方程的根,所以方程有两个根,…
设φ(x)=,则φ′(x)=,当x<0时,φ'(x)<0,φ(x)单调递减;
当0<x<1时,φ′(x)<0,φ(x)单调递减;当x>1时,φ′(x)>0,φ(x)单调递增.
故要使方程2a=有两个根,只需2a>φ(1)=e,即a>,
所以a的取值范围是(,+∞),
(3)由(2)得:0<x1<1<x2…
且由h'(x1)=0,得2ax1﹣=0,所以a=,x1∈(0,1)…
所以f′(x1)=h(x1)=a﹣=(﹣1),x1∈(0,1),
令r(t)=et(﹣1),(0<t<1),则r′(t)=et()<0,
r(t)在(0,1)上单调递减,
所以r(1)<r(t)<r(0),即﹣<f′(x1)<﹣1.…
22.【解答】(1)证明:由以D为圆心DA为半径作圆,
而ABCD为正方形,∴EA为圆D的切线
依据切割线定理,得EA2=EFEC…
另外圆O以BC为直径,∴EB是圆O的切线,
同样依据切割线定理得EB2=EFEC…
故AE=EB…
(2)解:连结BF,∵BC为圆O直径,
∴BF⊥EC
在RT△EBC中,有…
又在Rt△BCE中,
由射影定理得EFFC=BF2=.…
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
23.解:(Ⅰ)消去参数α得曲线C1的普通方程C1:x2+y2﹣2x=0.…(1)
将曲线C2:ρ=4sinθ化为直角坐标方程得x2+y2﹣4y=0.…(2)
由(1)﹣(2)得4y﹣2x=0,即为直线AB的方程,故直线AB的斜率为;
(Ⅱ)由C1:(x﹣1)2+y2=1知曲线C1是以C1(1,0)为圆心,半径为1的圆,
由C2:x2+(y﹣2)2=4知曲线C2:是以C2(0,2)为圆心,半径为2的圆.
∵|AB|≤|AC1|+|C1C2|+|BC2|,
∴当|AB|取最大值时,圆心C1,C2在直线AB上,
∴直线AB(即直线C1C2)的方程为:2x+y=2.
∵O到直线AB的距离为,
又此时|AB|=|C1C2|+1+2=3+,
∴△AOB的面积为.
24.(Ⅰ)解:函数f(x)=|x﹣|﹣|2x+1|=
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com ),
函数的图象如图所示,则函数的值域为(﹣∞,1];
( http: / / www.21cnjy.com )
(Ⅱ)证明:由题意x,y,z均为正实数,x+y+z=1,
由柯西不等式可得(x+y+z)(++)≥(y+z+z)2=1,
∴++≥1.
同课章节目录
