2.5 向量的应用

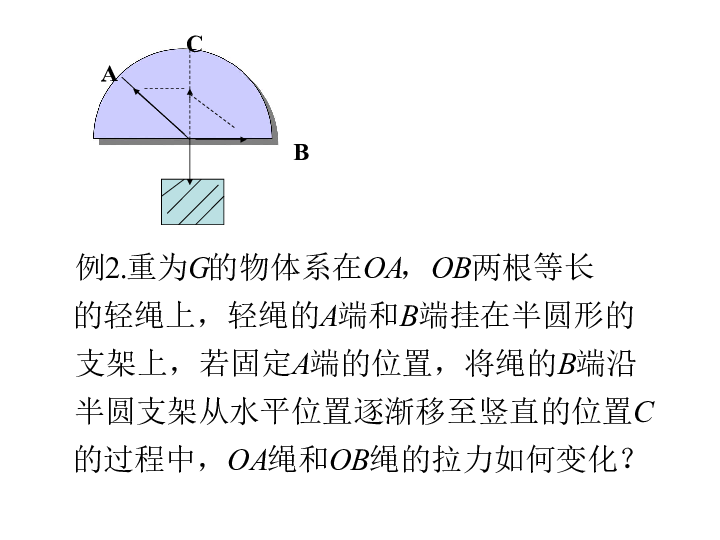
课件17张PPT。第2章 平面向量§2.5 向量的应用向量在物理中的应用举例ACB【思考】日常生活中,我们有时要用同样长的两根绳子挂一个物体(如图).如果绳子的最大拉力为F,物体受到的重力为G。你能否用向量的知识分析绳子受到的拉力F1的大小与两绳之间的夹角θ的关系？总结:用向量中的有关知识研究物理中的相关问题,步骤如下1.问题的转化,即把物理问题转化为数学问题.
2.模型的建立,即建立以向量为主题的数学模型.
3.参数的获得,即求出数学模型的有关解------理论参数值.
4.问题的答案,即回到问题的初始状态,解释相关的物理现象.平面几何中的向量方法 向量概念和运算，都有明确的物理背景和几何背景。当向量与平面坐标系结合以后，向量的运算就可以完全转化为“代数”的计算，这就为我们解决物理问题和几何研究带来极大的方便。
由于向量的线性运算和数量积运算具有鲜明的几何背景，平面几何的许多性质，如平移、全等、相似、长度、夹角都可以由向量的线性运算及数量积表示出来，因此，利用向量方法可以解决平面几何中的一些问题。问题：平行四边形是表示向量加法与减法的几何模型。如图，你能发现平行四边形对角线的长度与两条邻边长度之间的关系吗？猜想：1.长方形对角线的长度与两条邻边长度之间有何关系？2.类比猜想，平行四边形有相似关系吗？例1、证明平行四边形四边平方和等于两对角线平方和已知：平行四边形ABCD。
求证：解：设 ，则
分析：因为平行四边形对边平行且相
等，故设 其它线段对应向
量用它们表示。∴你能总结一下利用向量法解决平面几何问题的基本思路吗？（1）建立平面几何与向量的联系，用向量表示问题中涉及的几何元素，将平面几何问题转化为向量问题；
（2）通过向量运算，研究几何元素之间的关系，如距离、夹角等问题；
（3）把运算结果“翻译”成几何元素。用向量方法解决平面几何问题的“三步曲”：简述：形到向量 向量的运算 向量和数到形例2 如图，平行四边形ABCD中，点E、F分别是AD 、 DC边的中点，BE 、 BF分别与AC交于R 、 T两点，你能发现AR 、 RT 、TC之间的关系吗？猜想：
AR=RT=TC解：设 则由于 与 共线，故设又因为 共线，
所以设因为
所以线，故AT=RT=TC练习、证明直径所对的圆周角是直角分析：要证∠ACB=90°，只须证向
量 ，即 。解：设
则 ，
由此可得：即 ，∠ACB=90°思考：能否用向量
坐标形式证明？（1）建立平面几何与向量的联系，用向量表示问题中涉及的几何元素，将平面几何问题转化为向量问题；
（2）通过向量运算，研究几何元素之间的关系，如距离、夹角等问题；
（3）把运算结果“翻译”成几何元素。小结：用向量方法解决平面几何问题的“三步曲”：