4.5垂线同步练习
图片预览



文档简介
湘教版七年级下册数学4.5垂线同步练习
一、选择题(本大题共8小题)
1. 体育课上,老师测量跳远成绩的依据是( )
A.平行线间的距离相等 B.两点之间,线段最短
C.垂线段最短 D.两点确定一条直线
2. 已知直线AB,CB,l在同一平面内,若AB⊥l,垂足为B,CB⊥l,垂足也为B,则符合题意的图形可以是( )
A.B.C.D.
3. 如图所示,已知AC⊥BC,CD⊥AB,垂足分别是C,D,那么以下线段大小的比较必定成立的是( )
A.CD>AD B.AC<BC C.BC>BD D.CD<BD
4. 如图,直线l1∥l2,l3⊥l4,∠1=44°,那么∠2的度数( )
A. 46° B. 44° C. 36° D. 22°
5. 如图,直线a∥b,c⊥a,则c与b相交所形成的∠2度数为( )
A. 45° B.60° C. 90° D. 120°
6. 下列叙述中,正确的是( )
A.相等的两个角是对顶角
B.一条直线有只有一条垂线
C.从直线外一点到这条直线上的各点所连接的线段中,垂线段最短
D.一个角一定不等于它的余角
7. 如图,AB∥EF,CD⊥EF,∠BAC=50°,则∠ACD=( )
A. 120° B. 130° C. 140° D. 150°
8. 如图,直线a∥b,直线l与a相交于点P,与直线b相交于点Q,PM⊥l于点P,若∠1=50°,则∠2为( ).
A. 40° B. 30° C. 50° D. 60°
二、填空题(本大题共6小题)
9. 如图, 直线AB、CD相交于点E,EF⊥AB于E,若∠CEF=59°,则∠AED的度数为 .
10. 如图所示,直线∥.直线与直线,分别相交于点、点,,垂足为点,若,则= _________
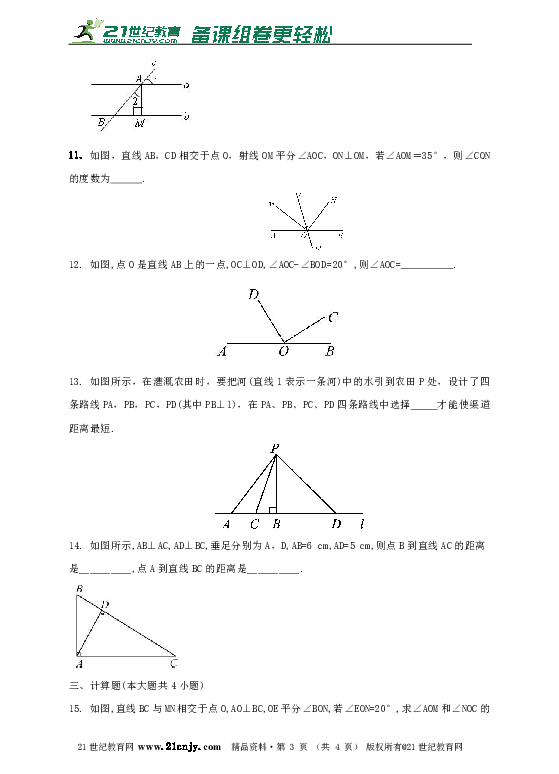
11. 如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON的度数为 .
12. 如图,点O是直线AB上的一点,OC⊥OD,∠AOC-∠BOD=20°,则∠AOC= .
13. 如图所示,在灌溉农田时,要把河(直线l表示一条河)中的水引到农田P处,设计了四条路线PA,PB,PC,PD(其中PB⊥l),在PA、PB、PC、PD四条路线中选择 才能使渠道距离最短.
14. 如图所示,AB⊥AC,AD⊥BC,垂足分别为A,D,AB=6 cm,AD=5 cm,则点B到直线AC的距离是__________,点A到直线BC的距离是__________.
三、计算题(本大题共4小题)
15. 如图,直线BC与MN相交于点O,AO⊥BC,OE平分∠BON,若∠EON=20°,求∠AOM和∠NOC的度数.
16. 如图所示,O为直线AB上一点,∠AOC=∠BOC,OC是∠AOD的平分线.
(1)求∠COD的度数;(2)判断OD与AB的位置关系,并说明理由.
17. 如图所示,直线AB,CD相交于点O,作∠DOE=∠BOD,OF平分∠AOE.
(1)判断OF与OD的位置关系;
(2)若∠AOC∶∠AOD=1∶5,求∠EOF的度数.
18. 如图所示,一辆汽车在直线形的公路AB上由A向B行驶,M,N分别是?位于公路AB两侧的村庄,设汽车行驶到P点位置时,离村庄M最近,行驶到Q点位置时,离村庄N最近,请你在AB上分别画出P,Q两点的位置.
参考答案:
一、选择题(本大题共8小题)
1. C
分析:此题为数学知识的应用,由实际出发,老师测量跳远成绩的依据是垂线段最短.
解:体育课上,老师测量跳远成绩的依据是垂线段最短.
故选:C.
2.C
分析:根据题意画出图形即可.
解:根据题意可得图形
,
故选:C.
3. C
分析:根据从直线外一点到这条直线上各点所连的线段中,垂线段最短进行分析.
解:A、CD与AD互相垂直,没有明确的大小关系,错误;
B、AC与BC互相垂直,没有明确的大小关系,错误;
C、BD是从直线CD外一点B所作的垂线段,根据垂线段最短定理,BC>BD,正确;
D、CD与BD互相垂直,没有明确的大小关系,错误,故选C.
4. A
分析:根据两直线平行,内错角相等可得∠3=∠1,再根据直角三角形两锐角互余列式计算即可得解
解:∵l1∥l2,
∴∠3=∠1=44°,
∵l3⊥l4,
∴∠2=90°﹣∠3=90°﹣44°=46°.
故选A.
5. C
分析:根据垂线的定义可得∠1=90°,再根据两直线平行,同位角相等可得∠2=∠1.
解:∵c⊥a,
∴∠1=90°,
∵a∥b,
∴∠2=∠1=90°.
故选C.
6. C
分析:根据对顶角的定义,垂线的性质,余角的定义作答.
解:A、直角都相等,但不一定是对顶角,故本选项错误;
B、一条直线有无数条垂线,故本选项错误;
C、从直线外一点到这条直线上的各点所连接的线段中,垂线段最短是对的,正确;
D、45°角等于它的余角,故本选项错误.
故选C.
7. C
分析: 如图,作辅助线;首先运用平行线的性质求出∠DGC的度数,借助三角形外角的性质求出∠ACD即可解决问题.
解:如图,延长AC交EF于点G;
∵AB∥EF,
∴∠DGC=∠BAC=50°;
∵CD⊥EF,
∴∠CDG=90°,
∴∠ACD=90°+50°=140°,
故选C.
8. A
分析:根据两直线平行,内错角相等,即可求得∠3=∠1,根据PM⊥l于点P,则∠MPQ=90°,即可求解.
解:∵直线a∥b,
∴∠3=∠1=50°,
又∵PM⊥l于点P,
∴∠MPQ=90°,
∴∠2=90°﹣∠3=90°﹣50°=40°.
故答案是:40.故选A。
二、填空题(本大题共6小题)
9. 分析:先根据垂直的定义求出∠ACE的度数,再根据平角等于180°列式计算即可得解.
解:∵EF⊥AB于E,∠CEF=59°,
∴∠ACE=90°-∠CEF=90°-59°=31°
∴∠AED=180°-∠ACE=180°-31°=149°.
故答案为:149°.
10. 分析:因为,所以∠ABM=∠1=58°.又因为AM⊥,所以∠2+∠ABM=90°,所以∠2=90°-58°=32°.
解答:32°
11. 分析:根据垂线和角平分线的概念可得。
解:∵射线OM平分∠AOC,∠AOM=35°,
∴∠MOC=35°,
∵ON⊥OM,
∴∠MON=90°,
∴∠CON=∠MON﹣∠MOC=90°﹣35°=55°.
12. 分析:主要考查你对余角,补角??等考点的理解。
解:∵OC⊥OD,
∴∠COD=90°,
∵∠AOD+∠COD+∠COB=∠AOB=180°,
∴∠AOD+∠COB=90°,①
∵∠AOC-∠BOD=20°,
即∠AOD+∠COD-∠COD-∠BOC=20°,
∴∠AOD-∠BOC=20°,②
联立①、②求得,
∠AOD=55°,∠BOC=35°,
∴∠AOC=∠COD+∠AOD=90°+55°=145°.
13. 分析:根据垂线段性质,点到直线的线段中垂线段最短可以得到解答.
解:∵垂线段最短,又∵PB⊥l
∴选PB。
14. 分析:考查了垂线段的知识点,注意垂直关系时解题关键。
解:根据图形可得点B到直线AC的距离是AB,为6cm,点A到直线BC的距离是AD,是5cm.
三、计算题(本大题共4小题)
15. 分析:要求∠AOM的度数,可先求它的余角.由已知∠EON=20°,结合角平分线的概念,即可求得∠BON.再根据对顶角相等即可求得;要求∠NOC的度数,根据邻补角的定义即可.
解:∵OE平分∠BON,
∴∠BON=2∠EON=2×20°=40°,
∴∠NOC=180°-∠BON=180°-40°=140°,
∠MOC=∠BON=40°,
∵AO⊥BC,
∴∠AOC=90°,
∴∠AOM=∠AOC-∠MOC=90°-40°=50°,
所以∠NOC=140°,∠AOM=50°.
16.分析:主要考查了垂线、角平分线等概念的应用,灵活把握角之间的关系即可。
解; 解:(1)∵∠AOC+∠BOC=180°,∠AOC=∠BOC,
∴∠BOC+∠BOC=180°,解得∠BOC=135°,
∴∠AOC=180°﹣∠BOC=180°﹣135°=45°,
∵OC平分∠AOD,
∴∠COD=∠AOC=45°.
(2)OD⊥AB.
理由:由(1)知∠AOC=∠COD=45°,
∴∠AOD=∠AC+∠COD=90°,
∴OD⊥AB(垂直定义).
17. 解:由题知∠BOD=∠AOC=28°(对顶角相等)
因为∠DOE=∠BOD
所以∠BOE=2∠BOD=56°
因为∠AOE+∠BOE=180°
所以∠AOE=124°
因为OF平分∠AOE
所以∠EOF=∠AOE=62°。
18. 分析:根据点到直线的距离垂线段最短可作图;本题主要考查了点到直线的距离垂线段最短的实际运用.利用尺规可作图,通过图形来分析题意可快捷的求解.
解:如图所示.
一、选择题(本大题共8小题)
1. 体育课上,老师测量跳远成绩的依据是( )
A.平行线间的距离相等 B.两点之间,线段最短
C.垂线段最短 D.两点确定一条直线
2. 已知直线AB,CB,l在同一平面内,若AB⊥l,垂足为B,CB⊥l,垂足也为B,则符合题意的图形可以是( )
A.B.C.D.
3. 如图所示,已知AC⊥BC,CD⊥AB,垂足分别是C,D,那么以下线段大小的比较必定成立的是( )
A.CD>AD B.AC<BC C.BC>BD D.CD<BD
4. 如图,直线l1∥l2,l3⊥l4,∠1=44°,那么∠2的度数( )
A. 46° B. 44° C. 36° D. 22°
5. 如图,直线a∥b,c⊥a,则c与b相交所形成的∠2度数为( )
A. 45° B.60° C. 90° D. 120°
6. 下列叙述中,正确的是( )
A.相等的两个角是对顶角
B.一条直线有只有一条垂线
C.从直线外一点到这条直线上的各点所连接的线段中,垂线段最短
D.一个角一定不等于它的余角
7. 如图,AB∥EF,CD⊥EF,∠BAC=50°,则∠ACD=( )
A. 120° B. 130° C. 140° D. 150°
8. 如图,直线a∥b,直线l与a相交于点P,与直线b相交于点Q,PM⊥l于点P,若∠1=50°,则∠2为( ).
A. 40° B. 30° C. 50° D. 60°
二、填空题(本大题共6小题)
9. 如图, 直线AB、CD相交于点E,EF⊥AB于E,若∠CEF=59°,则∠AED的度数为 .
10. 如图所示,直线∥.直线与直线,分别相交于点、点,,垂足为点,若,则= _________
11. 如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON的度数为 .
12. 如图,点O是直线AB上的一点,OC⊥OD,∠AOC-∠BOD=20°,则∠AOC= .
13. 如图所示,在灌溉农田时,要把河(直线l表示一条河)中的水引到农田P处,设计了四条路线PA,PB,PC,PD(其中PB⊥l),在PA、PB、PC、PD四条路线中选择 才能使渠道距离最短.
14. 如图所示,AB⊥AC,AD⊥BC,垂足分别为A,D,AB=6 cm,AD=5 cm,则点B到直线AC的距离是__________,点A到直线BC的距离是__________.
三、计算题(本大题共4小题)
15. 如图,直线BC与MN相交于点O,AO⊥BC,OE平分∠BON,若∠EON=20°,求∠AOM和∠NOC的度数.
16. 如图所示,O为直线AB上一点,∠AOC=∠BOC,OC是∠AOD的平分线.
(1)求∠COD的度数;(2)判断OD与AB的位置关系,并说明理由.
17. 如图所示,直线AB,CD相交于点O,作∠DOE=∠BOD,OF平分∠AOE.
(1)判断OF与OD的位置关系;
(2)若∠AOC∶∠AOD=1∶5,求∠EOF的度数.
18. 如图所示,一辆汽车在直线形的公路AB上由A向B行驶,M,N分别是?位于公路AB两侧的村庄,设汽车行驶到P点位置时,离村庄M最近,行驶到Q点位置时,离村庄N最近,请你在AB上分别画出P,Q两点的位置.
参考答案:
一、选择题(本大题共8小题)
1. C
分析:此题为数学知识的应用,由实际出发,老师测量跳远成绩的依据是垂线段最短.
解:体育课上,老师测量跳远成绩的依据是垂线段最短.
故选:C.
2.C
分析:根据题意画出图形即可.
解:根据题意可得图形
,
故选:C.
3. C
分析:根据从直线外一点到这条直线上各点所连的线段中,垂线段最短进行分析.
解:A、CD与AD互相垂直,没有明确的大小关系,错误;
B、AC与BC互相垂直,没有明确的大小关系,错误;
C、BD是从直线CD外一点B所作的垂线段,根据垂线段最短定理,BC>BD,正确;
D、CD与BD互相垂直,没有明确的大小关系,错误,故选C.
4. A
分析:根据两直线平行,内错角相等可得∠3=∠1,再根据直角三角形两锐角互余列式计算即可得解
解:∵l1∥l2,
∴∠3=∠1=44°,
∵l3⊥l4,
∴∠2=90°﹣∠3=90°﹣44°=46°.
故选A.
5. C
分析:根据垂线的定义可得∠1=90°,再根据两直线平行,同位角相等可得∠2=∠1.
解:∵c⊥a,
∴∠1=90°,
∵a∥b,
∴∠2=∠1=90°.
故选C.
6. C
分析:根据对顶角的定义,垂线的性质,余角的定义作答.
解:A、直角都相等,但不一定是对顶角,故本选项错误;
B、一条直线有无数条垂线,故本选项错误;
C、从直线外一点到这条直线上的各点所连接的线段中,垂线段最短是对的,正确;
D、45°角等于它的余角,故本选项错误.
故选C.
7. C
分析: 如图,作辅助线;首先运用平行线的性质求出∠DGC的度数,借助三角形外角的性质求出∠ACD即可解决问题.
解:如图,延长AC交EF于点G;
∵AB∥EF,
∴∠DGC=∠BAC=50°;
∵CD⊥EF,
∴∠CDG=90°,
∴∠ACD=90°+50°=140°,
故选C.
8. A
分析:根据两直线平行,内错角相等,即可求得∠3=∠1,根据PM⊥l于点P,则∠MPQ=90°,即可求解.
解:∵直线a∥b,
∴∠3=∠1=50°,
又∵PM⊥l于点P,
∴∠MPQ=90°,
∴∠2=90°﹣∠3=90°﹣50°=40°.
故答案是:40.故选A。
二、填空题(本大题共6小题)
9. 分析:先根据垂直的定义求出∠ACE的度数,再根据平角等于180°列式计算即可得解.
解:∵EF⊥AB于E,∠CEF=59°,
∴∠ACE=90°-∠CEF=90°-59°=31°
∴∠AED=180°-∠ACE=180°-31°=149°.
故答案为:149°.
10. 分析:因为,所以∠ABM=∠1=58°.又因为AM⊥,所以∠2+∠ABM=90°,所以∠2=90°-58°=32°.
解答:32°
11. 分析:根据垂线和角平分线的概念可得。
解:∵射线OM平分∠AOC,∠AOM=35°,
∴∠MOC=35°,
∵ON⊥OM,
∴∠MON=90°,
∴∠CON=∠MON﹣∠MOC=90°﹣35°=55°.
12. 分析:主要考查你对余角,补角??等考点的理解。
解:∵OC⊥OD,
∴∠COD=90°,
∵∠AOD+∠COD+∠COB=∠AOB=180°,
∴∠AOD+∠COB=90°,①
∵∠AOC-∠BOD=20°,
即∠AOD+∠COD-∠COD-∠BOC=20°,
∴∠AOD-∠BOC=20°,②
联立①、②求得,
∠AOD=55°,∠BOC=35°,
∴∠AOC=∠COD+∠AOD=90°+55°=145°.
13. 分析:根据垂线段性质,点到直线的线段中垂线段最短可以得到解答.
解:∵垂线段最短,又∵PB⊥l
∴选PB。
14. 分析:考查了垂线段的知识点,注意垂直关系时解题关键。
解:根据图形可得点B到直线AC的距离是AB,为6cm,点A到直线BC的距离是AD,是5cm.
三、计算题(本大题共4小题)
15. 分析:要求∠AOM的度数,可先求它的余角.由已知∠EON=20°,结合角平分线的概念,即可求得∠BON.再根据对顶角相等即可求得;要求∠NOC的度数,根据邻补角的定义即可.
解:∵OE平分∠BON,
∴∠BON=2∠EON=2×20°=40°,
∴∠NOC=180°-∠BON=180°-40°=140°,
∠MOC=∠BON=40°,
∵AO⊥BC,
∴∠AOC=90°,
∴∠AOM=∠AOC-∠MOC=90°-40°=50°,
所以∠NOC=140°,∠AOM=50°.
16.分析:主要考查了垂线、角平分线等概念的应用,灵活把握角之间的关系即可。
解; 解:(1)∵∠AOC+∠BOC=180°,∠AOC=∠BOC,
∴∠BOC+∠BOC=180°,解得∠BOC=135°,
∴∠AOC=180°﹣∠BOC=180°﹣135°=45°,
∵OC平分∠AOD,
∴∠COD=∠AOC=45°.
(2)OD⊥AB.
理由:由(1)知∠AOC=∠COD=45°,
∴∠AOD=∠AC+∠COD=90°,
∴OD⊥AB(垂直定义).
17. 解:由题知∠BOD=∠AOC=28°(对顶角相等)
因为∠DOE=∠BOD
所以∠BOE=2∠BOD=56°
因为∠AOE+∠BOE=180°
所以∠AOE=124°
因为OF平分∠AOE
所以∠EOF=∠AOE=62°。
18. 分析:根据点到直线的距离垂线段最短可作图;本题主要考查了点到直线的距离垂线段最短的实际运用.利用尺规可作图,通过图形来分析题意可快捷的求解.
解:如图所示.
