广东省河源市东江中学2016-2017学年高一(上)期末数学试卷(解析版)
文档属性
| 名称 | 广东省河源市东江中学2016-2017学年高一(上)期末数学试卷(解析版) |
|
|
| 格式 | zip | ||
| 文件大小 | 268.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-21 00:00:00 | ||
图片预览



文档简介
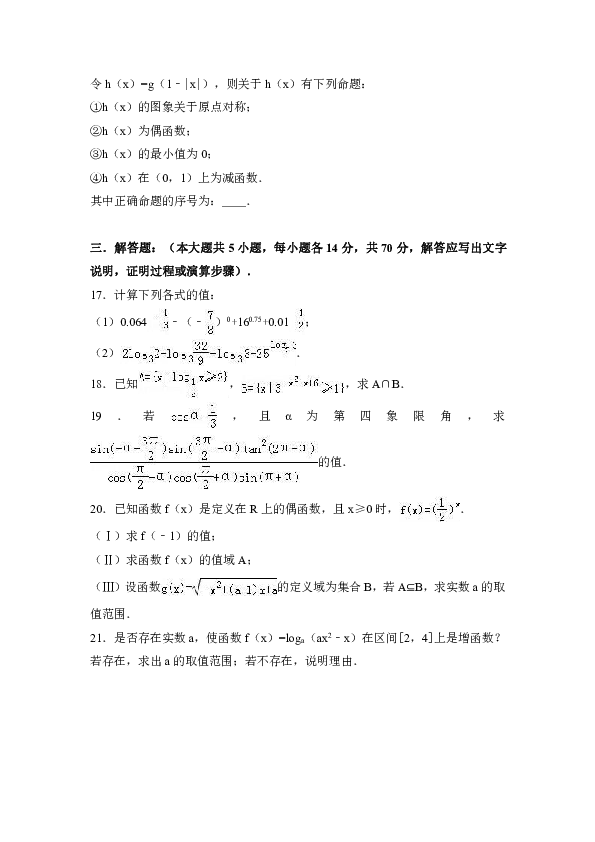
2016-2017学年广东省河源市东江中学高一(上)期末数学试卷
一.选择题:(本大题共12小题;每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.用列举法表示集合{(x,y)|},正确的是( )
A.(﹣1,1),(0,0)
B.{(﹣1,1),(0,0)}
C.{x=﹣1或0,y=1或0}
D.{﹣1,0,1}
2.函数f(x)=+lg(3x+1)的定义域是( )
A.(﹣,+∞)
B.(﹣,1)
C.(﹣,)
D.(﹣∞,﹣)
3.已知cosα=,角α是第二象限角,则tan(2π﹣α)等于( )
A.
B.﹣
C.
D.﹣
4.函数f(x)=2x+3x的零点所在的一个区间( )
A.(﹣2,﹣1)
B.(﹣1,0)
C.(0,1)
D.(1,2)
5.设函数f(x)=,则f(f(3))=( )
A.
B.3
C.
D.
6.已知,b=log23,c=1,d=3﹣0.5,那么( )
A.d<a<c<b
B.d<c<a<b
C.a<b<c<d
D.a<d<c<b
7.函数的图象是( )
A.
B.
C.
D.
8.已知函数y=x2﹣2x+3在闭区间[0,m]上有最大值3,最小值2,则m的取值范围是( )
A.[1,+∞)
B.[0,2]
C.[1,2]
D.(﹣∞,2]
9.给定函数①,②,③y=|x﹣1|,④y=2x+1,其中在区间(0,1)上单调递减的函数序号是( )
A.①②
B.②③
C.③④
D.①④
10.已知cos(+α)=﹣,则sin(α﹣)的值为( )
A.
B.﹣
C.
D.﹣
11.已知函数f(x)=单调递减,那么实数a的取值范围是( )
A.(0,1)
B.(0,)
C.[,)
D.[,1)
12.已知f(x)=2+log3x(1≤x≤9),则函数y=[f(x)]2+f(x2)的最大值为( )
A.6
B.13
C.22
D.33
二.填空题(本大题共4个小题,每小题5分,共20分)
13.cos(﹣π)+sin(﹣π)的值是 .
14.已知y=f(x)是奇函数,若g(x)=f(x)+2且g(1)=1,则g(﹣1)= .
15.若函数f(x)=ax﹣x﹣a(a>0,且a≠1)有两个零点,则实数a的取值范围是 .
16.已知函数f(x)=()x的图象与函数g(x)的图象关于直线y=x对称,令h(x)=g(1﹣|x|),则关于h(x)有下列命题:
①h(x)的图象关于原点对称;
②h(x)为偶函数;
③h(x)的最小值为0;
④h(x)在(0,1)上为减函数.
其中正确命题的序号为: .
三.解答题:(本大题共5小题,每小题各14分,共70分,解答应写出文字说明,证明过程或演算步骤).
17.计算下列各式的值:
(1)0.064﹣(﹣)0+160.75+0.01;
(2).
18.已知,,求A∩B.
19.若,且α为第四象限角,求的值.
20.已知函数f(x)是定义在R上的偶函数,且x≥0时,.
(Ⅰ)求f(﹣1)的值;
(Ⅱ)求函数f(x)的值域A;
(Ⅲ)设函数的定义域为集合B,若A B,求实数a的取值范围.
21.是否存在实数a,使函数f(x)=loga(ax2﹣x)在区间[2,4]上是增函数?若存在,求出a的取值范围;若不存在,说明理由.
2016-2017学年广东省河源市东江中学高一(上)期末数学试卷
参考答案与试题解析
一.选择题:(本大题共12小题;每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.用列举法表示集合{(x,y)|},正确的是( )
A.(﹣1,1),(0,0)
B.{(﹣1,1),(0,0)}
C.{x=﹣1或0,y=1或0}
D.{﹣1,0,1}
【考点】集合的表示法.
【分析】解方程组,能用列举法表示所求集合.
【解答】解:集合{(x,y)|}={(﹣1,1),(0,0)},
故选:B.
2.函数f(x)=+lg(3x+1)的定义域是( )
A.(﹣,+∞)
B.(﹣,1)
C.(﹣,)
D.(﹣∞,﹣)
【考点】对数函数的定义域;函数的定义域及其求法.
【分析】依题意可知要使函数有意义需要1﹣x>0且3x+1>0,进而可求得x的范围.
【解答】解:要使函数有意义需,
解得﹣<x<1.
故选B.
3.已知cosα=,角α是第二象限角,则tan(2π﹣α)等于( )
A.
B.﹣
C.
D.﹣
【考点】三角函数的化简求值;同角三角函数基本关系的运用.
【分析】由已知结合同角三角函数基本关系式求得sinα,再由诱导公式及同角三角函数的基本关系式求解.
【解答】解:∵cosα=,角α是第二象限角,
∴sinα=.
∴tan(2π﹣α)=﹣tanα=﹣.
故选:C.
4.函数f(x)=2x+3x的零点所在的一个区间( )
A.(﹣2,﹣1)
B.(﹣1,0)
C.(0,1)
D.(1,2)
【考点】函数零点的判定定理.
【分析】判断函数的单调性,利用f(﹣1)与f(0)函数值的大小,通过零点判定定理判断即可.
【解答】解:函数f(x)=2x+3x是增函数,
f(﹣1)=<0,f(0)=1+0=1>0,
可得f(﹣1)f(0)<0.
由零点判定定理可知:函数f(x)=2x+3x的零点所在的一个区间(﹣1,0).
故选:B.
5.设函数f(x)=,则f(f(3))=( )
A.
B.3
C.
D.
【考点】函数的值.
【分析】由条件求出f(3)=,结合函数解析式求出
f(f(3))=f()=+1,计算求得结果.
【解答】解:函数f(x)=,则f(3)=,
∴f(f(3))=f()=+1=,
故选D.
6.已知,b=log23,c=1,d=3﹣0.5,那么( )
A.d<a<c<b
B.d<c<a<b
C.a<b<c<d
D.a<d<c<b
【考点】不等式比较大小.
【分析】由函数y=,y=log2x和y=3x的单调性可得a<0,b>1,0<d<1,可得答案.
【解答】解:因为对数函数y=单调递减,故<=0;
同理因为对数函数y=log2x单调递增,故b=log23>log22=1;
由指数函数y=3x单调递增,故0<d=3﹣0.5<30=1,
综上可得a<d<c<b,
故选D
7.函数的图象是( )
A.
B.
C.
D.
【考点】幂函数的图象.
【分析】先找出函数图象上的特殊点(1,1),(8,2),(,),再判断函数的走向,结合图形,选出正确的答案.
【解答】解:函数图象上的特殊点(1,1),故排除A,D;
由特殊点(8,2),(,),可排除C.
故选B.
8.已知函数y=x2﹣2x+3在闭区间[0,m]上有最大值3,最小值2,则m的取值范围是( )
A.[1,+∞)
B.[0,2]
C.[1,2]
D.(﹣∞,2]
【考点】二次函数的性质.
【分析】本题利用数形结合法解决,作出函数f(x)的图象,如图所示,当x=1时,y最小,最小值是2,当x=2时,y=3,欲使函数f(x)=x2﹣2x+3在闭区间[0,m]上的上有最大值3,最小值2,则实数m的取值范围要大于等于1而小于等于2即可.
【解答】解:作出函数f(x)的图象,如图所示,
当x=1时,y最小,最小值是2,当x=2时,y=3,
函数f(x)=x2﹣2x+3在闭区间[0,m]上上有最大值3,最小值2,
则实数m的取值范围是[1,2].
故选:C
9.给定函数①,②,③y=|x﹣1|,④y=2x+1,其中在区间(0,1)上单调递减的函数序号是( )
A.①②
B.②③
C.③④
D.①④
【考点】函数单调性的判断与证明.
【分析】本题所给的四个函数分别是幂函数型,对数函数型,指数函数型,含绝对值函数型,在解答时需要熟悉这些函数类型的图象和性质;①为增函数,②为定义域上的减函数,③y=|x﹣1|有两个单调区间,一增区间一个减区间,④y=2x+1为增函数.
【解答】解:①是幂函数,其在(0,+∞)上即第一象限内为增函数,故此项不符合要求;
②中的函数是由函数向左平移1个单位长度得到的,因为原函数在(0,+∞)内为减函数,故此项符合要求;
③中的函数图象是由函数y=x﹣1的图象保留x轴上方,下方图象翻折到x轴上方而得到的,故由其图象可知该项符合要求;
④中的函数图象为指数函数,因其底数大于1,故其在R上单调递增,不合题意.
故选B.
10.已知cos(+α)=﹣,则sin(α﹣)的值为( )
A.
B.﹣
C.
D.﹣
【考点】两角和与差的正弦函数.
【分析】由条件利用诱导公式化简所给的三角函数式,可得结果.
【解答】解:∵cos(+α)=﹣,则sin(α﹣)=sin[﹣(+α)]=cos(+α)=﹣,
故选:B.
11.已知函数f(x)=单调递减,那么实数a的取值范围是( )
A.(0,1)
B.(0,)
C.[,)
D.[,1)
【考点】函数单调性的判断与证明.
【分析】根据指数函数与一次函数的单调性,列出不等式组求出a的取值范围.
【解答】解:函数f(x)=单调递减,
根据指数函数与一次函数的单调性知,
,
解得≤a<,
所以实数a的取值范围是[,).
故选:C.
12.已知f(x)=2+log3x(1≤x≤9),则函数y=[f(x)]2+f(x2)的最大值为( )
A.6
B.13
C.22
D.33
【考点】对数函数的值域与最值.
【分析】将f(x)=2+log3x(1≤x≤9)代入y=[f(x)]2+f(x2)中,整理化简为关于log3x的函数,利用换元法求最值.
【解答】解:y=[f(x)]2+f(x2)=(log3x)2+6log3x+6,
∵f(x)=2+log3x(1≤x≤9),
∴
∴y=[f(x)]2+f(x2)=(log3x)2+6log3x+6,的定义域是{x|1≤x≤3}.
令log3x=t,因为1≤x≤3,所以0≤t≤1,
则上式变为y=t2+6t+6,0≤t≤1,
y=t2+6t+6在[0,1]上是增函数
当t=1时,y取最大值13
故选B
二.填空题(本大题共4个小题,每小题5分,共20分)
13.cos(﹣π)+sin(﹣π)的值是 0 .
【考点】运用诱导公式化简求值.
【分析】由条件利用诱导公式进行化简所给的式子,可得结果.
【解答】解:cos(﹣π)+sin(﹣π)=cos(﹣)+sin(﹣)=cos﹣sin=﹣=0,
故答案为:0.
14.已知y=f(x)是奇函数,若g(x)=f(x)+2且g(1)=1,则g(﹣1)= 3 .
【考点】函数奇偶性的性质;函数的值.
【分析】由题意y=f(x)是奇函数,g(x)=f(x)+2得到g(x)+g(﹣x)=f(x)+2+f(﹣x)+2=4,再令x=1即可得到1+g(﹣1)=4,从而解出答案
【解答】解:由题意y=f(x)是奇函数,g(x)=f(x)+2
∴g(x)+g(﹣x)=f(x)+2+f(﹣x)+2=4
又g(1)=1
∴1+g(﹣1)=4,解得g(﹣1)=3
故答案为:3
15.若函数f(x)=ax﹣x﹣a(a>0,且a≠1)有两个零点,则实数a的取值范围是 (1,+∞) .
【考点】函数的零点.
【分析】根据题设条件,分别作出令g(x)=ax(a>0,且a≠1),h(x)=x+a,分0<a<1,a>1两种情况的图象,结合图象的交点坐标进行求解.
【解答】解:令g(x)=ax(a>0,且a≠1),h(x)=x+a,分0<a<1,a>1两种情况.
在同一坐标系中画出两个函数的图象,如图,若函数f(x)=ax﹣x﹣a有两个不同的零点,则函数g(x),h(x)的图象有两个不同的交点.根据画出的图象只有当a>1时符合题目要求.
故答案为:(1,+∞)
16.已知函数f(x)=()x的图象与函数g(x)的图象关于直线y=x对称,令h(x)=g(1﹣|x|),则关于h(x)有下列命题:
①h(x)的图象关于原点对称;
②h(x)为偶函数;
③h(x)的最小值为0;
④h(x)在(0,1)上为减函数.
其中正确命题的序号为: ②③ .
【考点】四种命题的真假关系;函数的最值及其几何意义;函数奇偶性的判断;奇偶函数图象的对称性.
【分析】根据题意画出h(x)的图象就一目了然.
【解答】解:根据题意可知g(x)=(x>0)
∴(1﹣|x|)>0
∴﹣1<x<1
∴函数h(x)的图象为
∴②③正确.
三.解答题:(本大题共5小题,每小题各14分,共70分,解答应写出文字说明,证明过程或演算步骤).
17.计算下列各式的值:
(1)0.064﹣(﹣)0+160.75+0.01;
(2).
【考点】根式与分数指数幂的互化及其化简运算;对数的运算性质.
【分析】(1)自己利用指数的运算法则,求出表达式的值即可.
(2)利用对数的运算法则求解即可.
【解答】解:(1)原式===;﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
(2)原式===log39﹣9=2﹣9=﹣7.﹣﹣﹣﹣
18.已知,,求A∩B.
【考点】交集及其运算.
【分析】根据对数以及指数的运算分别求出A、B,从而求出A∩B即可.
【解答】解:
={x|0<x≤},
={x|﹣2≤x≤3},
故A∩B={x|0<x≤}.
19.若,且α为第四象限角,求的值.
【考点】三角函数的化简求值.
【分析】利用三角函数的诱导公式化简,由,且α为第四象限角,利用同角三角函数间的基本关系求出sinα的值即可得答案.
【解答】解:
==,
∵,且α为第四象限角,
∴=.
∴==.
20.已知函数f(x)是定义在R上的偶函数,且x≥0时,.
(Ⅰ)求f(﹣1)的值;
(Ⅱ)求函数f(x)的值域A;
(Ⅲ)设函数的定义域为集合B,若A B,求实数a的取值范围.
【考点】偶函数;集合的包含关系判断及应用;函数的值域;函数的值.
【分析】(I)根据函数是偶函数,把﹣1转化到给出解析式的范围上,代入解析式可求.
(II)因为f(x)是定义在R上的偶函数,所以x≥0时函数值的取值集合就是函数f(x)的值域A,求出(x≥0)的取值集合即可.
(III)先写出x所要满足的一元二次不等式,因为A=(0,1] B,
法一:把不等式分解因式,很容易看出两根,一根为﹣1又B中含有正数,所以另一根一定大于﹣1得定义域B=[﹣1,a],得实数a的取值范围;
法二:设为函数,利用函数图象,(0,1]在图象与x轴的两交点之间,图象开中向上,x=0,x=1时对应的函数小于等于0,得不等式组,可求实数a的取值范围.
【解答】解:(I)∵函数f(x)是定义在R上的偶函数
∴f(﹣1)=f(1)
又x≥0时,
∴,即f(﹣1)=.
(II)由函数f(x)是定义在R上的偶函数,
可得函数f(x)的值域A即为
x≥0时,f(x)的取值范围,
当x≥0时,
故函数f(x)的值域A=(0,1].
(III)∵
定义域B={x|﹣x2+(a﹣1)x+a≥0}={x|x2﹣(a﹣1)x﹣a≤0}
方法一:由x2﹣(a﹣1)x﹣a≤0得(x﹣a)(x+1)≤0
∵A B∴B=[﹣1,a],且a≥1
∴实数a的取值范围是{a|a≥1}
方法二:设h(x)=x2﹣(a﹣1)x﹣a
A B当且仅当即
∴实数a的取值范围是{a|a≥1}
21.是否存在实数a,使函数f(x)=loga(ax2﹣x)在区间[2,4]上是增函数?若存在,求出a的取值范围;若不存在,说明理由.
【考点】复合函数的单调性.
【分析】设u(x)=ax2﹣x,显然二次函数u的对称轴为x=.分当a>1时和当0<a<1
两种情况,分别利用二次
函数的性质、复合函数的单调性、以及对数函数的定义域,求得a的范围,综合可得结论.
【解答】解:设u(x)=ax2﹣x,显然二次函数u的对称轴为x=.
①当a>1时,要使函数f(x)在[2,4]上为增函数,则u(x)=ax2﹣x
在[2,4]上为增函数,
故应有,解得
a>.…
综合可得,a>1.…
②当0<a<1
时,要使函数f(x)在[2,4]上为增函数,则u(x)=ax2﹣x
在[2,4]上为减函数,
应有,解得a∈ .…
综上,a>1时,函数f(x)=loga(ax2﹣x)在区间[2,4]上为增函数.…
2017年3月21日
一.选择题:(本大题共12小题;每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.用列举法表示集合{(x,y)|},正确的是( )
A.(﹣1,1),(0,0)
B.{(﹣1,1),(0,0)}
C.{x=﹣1或0,y=1或0}
D.{﹣1,0,1}
2.函数f(x)=+lg(3x+1)的定义域是( )
A.(﹣,+∞)
B.(﹣,1)
C.(﹣,)
D.(﹣∞,﹣)
3.已知cosα=,角α是第二象限角,则tan(2π﹣α)等于( )
A.
B.﹣
C.
D.﹣
4.函数f(x)=2x+3x的零点所在的一个区间( )
A.(﹣2,﹣1)
B.(﹣1,0)
C.(0,1)
D.(1,2)
5.设函数f(x)=,则f(f(3))=( )
A.
B.3
C.
D.
6.已知,b=log23,c=1,d=3﹣0.5,那么( )
A.d<a<c<b
B.d<c<a<b
C.a<b<c<d
D.a<d<c<b
7.函数的图象是( )
A.
B.
C.
D.
8.已知函数y=x2﹣2x+3在闭区间[0,m]上有最大值3,最小值2,则m的取值范围是( )
A.[1,+∞)
B.[0,2]
C.[1,2]
D.(﹣∞,2]
9.给定函数①,②,③y=|x﹣1|,④y=2x+1,其中在区间(0,1)上单调递减的函数序号是( )
A.①②
B.②③
C.③④
D.①④
10.已知cos(+α)=﹣,则sin(α﹣)的值为( )
A.
B.﹣
C.
D.﹣
11.已知函数f(x)=单调递减,那么实数a的取值范围是( )
A.(0,1)
B.(0,)
C.[,)
D.[,1)
12.已知f(x)=2+log3x(1≤x≤9),则函数y=[f(x)]2+f(x2)的最大值为( )
A.6
B.13
C.22
D.33
二.填空题(本大题共4个小题,每小题5分,共20分)
13.cos(﹣π)+sin(﹣π)的值是 .
14.已知y=f(x)是奇函数,若g(x)=f(x)+2且g(1)=1,则g(﹣1)= .
15.若函数f(x)=ax﹣x﹣a(a>0,且a≠1)有两个零点,则实数a的取值范围是 .
16.已知函数f(x)=()x的图象与函数g(x)的图象关于直线y=x对称,令h(x)=g(1﹣|x|),则关于h(x)有下列命题:
①h(x)的图象关于原点对称;
②h(x)为偶函数;
③h(x)的最小值为0;
④h(x)在(0,1)上为减函数.
其中正确命题的序号为: .
三.解答题:(本大题共5小题,每小题各14分,共70分,解答应写出文字说明,证明过程或演算步骤).
17.计算下列各式的值:
(1)0.064﹣(﹣)0+160.75+0.01;
(2).
18.已知,,求A∩B.
19.若,且α为第四象限角,求的值.
20.已知函数f(x)是定义在R上的偶函数,且x≥0时,.
(Ⅰ)求f(﹣1)的值;
(Ⅱ)求函数f(x)的值域A;
(Ⅲ)设函数的定义域为集合B,若A B,求实数a的取值范围.
21.是否存在实数a,使函数f(x)=loga(ax2﹣x)在区间[2,4]上是增函数?若存在,求出a的取值范围;若不存在,说明理由.
2016-2017学年广东省河源市东江中学高一(上)期末数学试卷
参考答案与试题解析
一.选择题:(本大题共12小题;每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.用列举法表示集合{(x,y)|},正确的是( )
A.(﹣1,1),(0,0)
B.{(﹣1,1),(0,0)}
C.{x=﹣1或0,y=1或0}
D.{﹣1,0,1}
【考点】集合的表示法.
【分析】解方程组,能用列举法表示所求集合.
【解答】解:集合{(x,y)|}={(﹣1,1),(0,0)},
故选:B.
2.函数f(x)=+lg(3x+1)的定义域是( )
A.(﹣,+∞)
B.(﹣,1)
C.(﹣,)
D.(﹣∞,﹣)
【考点】对数函数的定义域;函数的定义域及其求法.
【分析】依题意可知要使函数有意义需要1﹣x>0且3x+1>0,进而可求得x的范围.
【解答】解:要使函数有意义需,
解得﹣<x<1.
故选B.
3.已知cosα=,角α是第二象限角,则tan(2π﹣α)等于( )
A.
B.﹣
C.
D.﹣
【考点】三角函数的化简求值;同角三角函数基本关系的运用.
【分析】由已知结合同角三角函数基本关系式求得sinα,再由诱导公式及同角三角函数的基本关系式求解.
【解答】解:∵cosα=,角α是第二象限角,
∴sinα=.
∴tan(2π﹣α)=﹣tanα=﹣.
故选:C.
4.函数f(x)=2x+3x的零点所在的一个区间( )
A.(﹣2,﹣1)
B.(﹣1,0)
C.(0,1)
D.(1,2)
【考点】函数零点的判定定理.
【分析】判断函数的单调性,利用f(﹣1)与f(0)函数值的大小,通过零点判定定理判断即可.
【解答】解:函数f(x)=2x+3x是增函数,
f(﹣1)=<0,f(0)=1+0=1>0,
可得f(﹣1)f(0)<0.
由零点判定定理可知:函数f(x)=2x+3x的零点所在的一个区间(﹣1,0).
故选:B.
5.设函数f(x)=,则f(f(3))=( )
A.
B.3
C.
D.
【考点】函数的值.
【分析】由条件求出f(3)=,结合函数解析式求出
f(f(3))=f()=+1,计算求得结果.
【解答】解:函数f(x)=,则f(3)=,
∴f(f(3))=f()=+1=,
故选D.
6.已知,b=log23,c=1,d=3﹣0.5,那么( )
A.d<a<c<b
B.d<c<a<b
C.a<b<c<d
D.a<d<c<b
【考点】不等式比较大小.
【分析】由函数y=,y=log2x和y=3x的单调性可得a<0,b>1,0<d<1,可得答案.
【解答】解:因为对数函数y=单调递减,故<=0;
同理因为对数函数y=log2x单调递增,故b=log23>log22=1;
由指数函数y=3x单调递增,故0<d=3﹣0.5<30=1,
综上可得a<d<c<b,
故选D
7.函数的图象是( )
A.
B.
C.
D.
【考点】幂函数的图象.
【分析】先找出函数图象上的特殊点(1,1),(8,2),(,),再判断函数的走向,结合图形,选出正确的答案.
【解答】解:函数图象上的特殊点(1,1),故排除A,D;
由特殊点(8,2),(,),可排除C.
故选B.
8.已知函数y=x2﹣2x+3在闭区间[0,m]上有最大值3,最小值2,则m的取值范围是( )
A.[1,+∞)
B.[0,2]
C.[1,2]
D.(﹣∞,2]
【考点】二次函数的性质.
【分析】本题利用数形结合法解决,作出函数f(x)的图象,如图所示,当x=1时,y最小,最小值是2,当x=2时,y=3,欲使函数f(x)=x2﹣2x+3在闭区间[0,m]上的上有最大值3,最小值2,则实数m的取值范围要大于等于1而小于等于2即可.
【解答】解:作出函数f(x)的图象,如图所示,
当x=1时,y最小,最小值是2,当x=2时,y=3,
函数f(x)=x2﹣2x+3在闭区间[0,m]上上有最大值3,最小值2,
则实数m的取值范围是[1,2].
故选:C
9.给定函数①,②,③y=|x﹣1|,④y=2x+1,其中在区间(0,1)上单调递减的函数序号是( )
A.①②
B.②③
C.③④
D.①④
【考点】函数单调性的判断与证明.
【分析】本题所给的四个函数分别是幂函数型,对数函数型,指数函数型,含绝对值函数型,在解答时需要熟悉这些函数类型的图象和性质;①为增函数,②为定义域上的减函数,③y=|x﹣1|有两个单调区间,一增区间一个减区间,④y=2x+1为增函数.
【解答】解:①是幂函数,其在(0,+∞)上即第一象限内为增函数,故此项不符合要求;
②中的函数是由函数向左平移1个单位长度得到的,因为原函数在(0,+∞)内为减函数,故此项符合要求;
③中的函数图象是由函数y=x﹣1的图象保留x轴上方,下方图象翻折到x轴上方而得到的,故由其图象可知该项符合要求;
④中的函数图象为指数函数,因其底数大于1,故其在R上单调递增,不合题意.
故选B.
10.已知cos(+α)=﹣,则sin(α﹣)的值为( )
A.
B.﹣
C.
D.﹣
【考点】两角和与差的正弦函数.
【分析】由条件利用诱导公式化简所给的三角函数式,可得结果.
【解答】解:∵cos(+α)=﹣,则sin(α﹣)=sin[﹣(+α)]=cos(+α)=﹣,
故选:B.
11.已知函数f(x)=单调递减,那么实数a的取值范围是( )
A.(0,1)
B.(0,)
C.[,)
D.[,1)
【考点】函数单调性的判断与证明.
【分析】根据指数函数与一次函数的单调性,列出不等式组求出a的取值范围.
【解答】解:函数f(x)=单调递减,
根据指数函数与一次函数的单调性知,
,
解得≤a<,
所以实数a的取值范围是[,).
故选:C.
12.已知f(x)=2+log3x(1≤x≤9),则函数y=[f(x)]2+f(x2)的最大值为( )
A.6
B.13
C.22
D.33
【考点】对数函数的值域与最值.
【分析】将f(x)=2+log3x(1≤x≤9)代入y=[f(x)]2+f(x2)中,整理化简为关于log3x的函数,利用换元法求最值.
【解答】解:y=[f(x)]2+f(x2)=(log3x)2+6log3x+6,
∵f(x)=2+log3x(1≤x≤9),
∴
∴y=[f(x)]2+f(x2)=(log3x)2+6log3x+6,的定义域是{x|1≤x≤3}.
令log3x=t,因为1≤x≤3,所以0≤t≤1,
则上式变为y=t2+6t+6,0≤t≤1,
y=t2+6t+6在[0,1]上是增函数
当t=1时,y取最大值13
故选B
二.填空题(本大题共4个小题,每小题5分,共20分)
13.cos(﹣π)+sin(﹣π)的值是 0 .
【考点】运用诱导公式化简求值.
【分析】由条件利用诱导公式进行化简所给的式子,可得结果.
【解答】解:cos(﹣π)+sin(﹣π)=cos(﹣)+sin(﹣)=cos﹣sin=﹣=0,
故答案为:0.
14.已知y=f(x)是奇函数,若g(x)=f(x)+2且g(1)=1,则g(﹣1)= 3 .
【考点】函数奇偶性的性质;函数的值.
【分析】由题意y=f(x)是奇函数,g(x)=f(x)+2得到g(x)+g(﹣x)=f(x)+2+f(﹣x)+2=4,再令x=1即可得到1+g(﹣1)=4,从而解出答案
【解答】解:由题意y=f(x)是奇函数,g(x)=f(x)+2
∴g(x)+g(﹣x)=f(x)+2+f(﹣x)+2=4
又g(1)=1
∴1+g(﹣1)=4,解得g(﹣1)=3
故答案为:3
15.若函数f(x)=ax﹣x﹣a(a>0,且a≠1)有两个零点,则实数a的取值范围是 (1,+∞) .
【考点】函数的零点.
【分析】根据题设条件,分别作出令g(x)=ax(a>0,且a≠1),h(x)=x+a,分0<a<1,a>1两种情况的图象,结合图象的交点坐标进行求解.
【解答】解:令g(x)=ax(a>0,且a≠1),h(x)=x+a,分0<a<1,a>1两种情况.
在同一坐标系中画出两个函数的图象,如图,若函数f(x)=ax﹣x﹣a有两个不同的零点,则函数g(x),h(x)的图象有两个不同的交点.根据画出的图象只有当a>1时符合题目要求.
故答案为:(1,+∞)
16.已知函数f(x)=()x的图象与函数g(x)的图象关于直线y=x对称,令h(x)=g(1﹣|x|),则关于h(x)有下列命题:
①h(x)的图象关于原点对称;
②h(x)为偶函数;
③h(x)的最小值为0;
④h(x)在(0,1)上为减函数.
其中正确命题的序号为: ②③ .
【考点】四种命题的真假关系;函数的最值及其几何意义;函数奇偶性的判断;奇偶函数图象的对称性.
【分析】根据题意画出h(x)的图象就一目了然.
【解答】解:根据题意可知g(x)=(x>0)
∴(1﹣|x|)>0
∴﹣1<x<1
∴函数h(x)的图象为
∴②③正确.
三.解答题:(本大题共5小题,每小题各14分,共70分,解答应写出文字说明,证明过程或演算步骤).
17.计算下列各式的值:
(1)0.064﹣(﹣)0+160.75+0.01;
(2).
【考点】根式与分数指数幂的互化及其化简运算;对数的运算性质.
【分析】(1)自己利用指数的运算法则,求出表达式的值即可.
(2)利用对数的运算法则求解即可.
【解答】解:(1)原式===;﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
(2)原式===log39﹣9=2﹣9=﹣7.﹣﹣﹣﹣
18.已知,,求A∩B.
【考点】交集及其运算.
【分析】根据对数以及指数的运算分别求出A、B,从而求出A∩B即可.
【解答】解:
={x|0<x≤},
={x|﹣2≤x≤3},
故A∩B={x|0<x≤}.
19.若,且α为第四象限角,求的值.
【考点】三角函数的化简求值.
【分析】利用三角函数的诱导公式化简,由,且α为第四象限角,利用同角三角函数间的基本关系求出sinα的值即可得答案.
【解答】解:
==,
∵,且α为第四象限角,
∴=.
∴==.
20.已知函数f(x)是定义在R上的偶函数,且x≥0时,.
(Ⅰ)求f(﹣1)的值;
(Ⅱ)求函数f(x)的值域A;
(Ⅲ)设函数的定义域为集合B,若A B,求实数a的取值范围.
【考点】偶函数;集合的包含关系判断及应用;函数的值域;函数的值.
【分析】(I)根据函数是偶函数,把﹣1转化到给出解析式的范围上,代入解析式可求.
(II)因为f(x)是定义在R上的偶函数,所以x≥0时函数值的取值集合就是函数f(x)的值域A,求出(x≥0)的取值集合即可.
(III)先写出x所要满足的一元二次不等式,因为A=(0,1] B,
法一:把不等式分解因式,很容易看出两根,一根为﹣1又B中含有正数,所以另一根一定大于﹣1得定义域B=[﹣1,a],得实数a的取值范围;
法二:设为函数,利用函数图象,(0,1]在图象与x轴的两交点之间,图象开中向上,x=0,x=1时对应的函数小于等于0,得不等式组,可求实数a的取值范围.
【解答】解:(I)∵函数f(x)是定义在R上的偶函数
∴f(﹣1)=f(1)
又x≥0时,
∴,即f(﹣1)=.
(II)由函数f(x)是定义在R上的偶函数,
可得函数f(x)的值域A即为
x≥0时,f(x)的取值范围,
当x≥0时,
故函数f(x)的值域A=(0,1].
(III)∵
定义域B={x|﹣x2+(a﹣1)x+a≥0}={x|x2﹣(a﹣1)x﹣a≤0}
方法一:由x2﹣(a﹣1)x﹣a≤0得(x﹣a)(x+1)≤0
∵A B∴B=[﹣1,a],且a≥1
∴实数a的取值范围是{a|a≥1}
方法二:设h(x)=x2﹣(a﹣1)x﹣a
A B当且仅当即
∴实数a的取值范围是{a|a≥1}
21.是否存在实数a,使函数f(x)=loga(ax2﹣x)在区间[2,4]上是增函数?若存在,求出a的取值范围;若不存在,说明理由.
【考点】复合函数的单调性.
【分析】设u(x)=ax2﹣x,显然二次函数u的对称轴为x=.分当a>1时和当0<a<1
两种情况,分别利用二次
函数的性质、复合函数的单调性、以及对数函数的定义域,求得a的范围,综合可得结论.
【解答】解:设u(x)=ax2﹣x,显然二次函数u的对称轴为x=.
①当a>1时,要使函数f(x)在[2,4]上为增函数,则u(x)=ax2﹣x
在[2,4]上为增函数,
故应有,解得
a>.…
综合可得,a>1.…
②当0<a<1
时,要使函数f(x)在[2,4]上为增函数,则u(x)=ax2﹣x
在[2,4]上为减函数,
应有,解得a∈ .…
综上,a>1时,函数f(x)=loga(ax2﹣x)在区间[2,4]上为增函数.…
2017年3月21日
同课章节目录
