3.3公式法 同步练习
图片预览



文档简介
湘教版七年级下册数学3.3公式法同步练习
一、选择题(本大题共8小题)
1. 分解因式:16﹣x2=( )
A.(4﹣x)(4+x) B.(x﹣4)(x+4) C.(8+x)(8﹣x) D.(4﹣x)2
2. 下列多项式能用平方差公式因式分解的是( )
A. a2+(-b) 2; B. 5m2-20mn; C. -x2-y2; D. -x2+9;21*cnjy*com
3. 若x2+2(m-3)+16是完全平方式,则m的值为( )
A. -5; B. 7; C. -1; D. 7或-1;
4. 一个多项式分解因式的结果是,那么这个多项式是( )
A. B. C. D.
5. 下列因式分解正确的是( )
A.x3-x=x(x-1) B.x2-y2=(x-y)2
C.-4x2+9y2=(2x+3y)(2x-3y) D.x2+6x+9=(x+3) 2
6. 利用因式分解简便计算57×99+44×99-99正确的是( )
A.99×(57+44)=9 999 B.99×(57+44-1)=9 900
C.99×(57+44+1)=10 098 D.99×(57+44-99)=198
7. 某同学粗心大意,因式分解时,把等式x4-■=(x2+4)(x+2)(x-▲)中的两个数弄污了,则式子中的■,▲对应得一组数可以是( )2·1·c·n·j·y
A. 8,1; B.16,2; C.24,3; D. 64,8;
8. 多项式ax2﹣4ax﹣12a因式分解正确的是( )
A.a(x﹣6)(x+2) B.a(x﹣3)(x+4)C.a(x2﹣4x﹣12)D. a(x+6)(x﹣2)
二、填空题(本大题共5小题)
9. 已知,则= .
10. 把多项式9a3﹣ab2分解因式的结果是 .
11. 分解因式:(m+1)(m﹣9)+8m= .
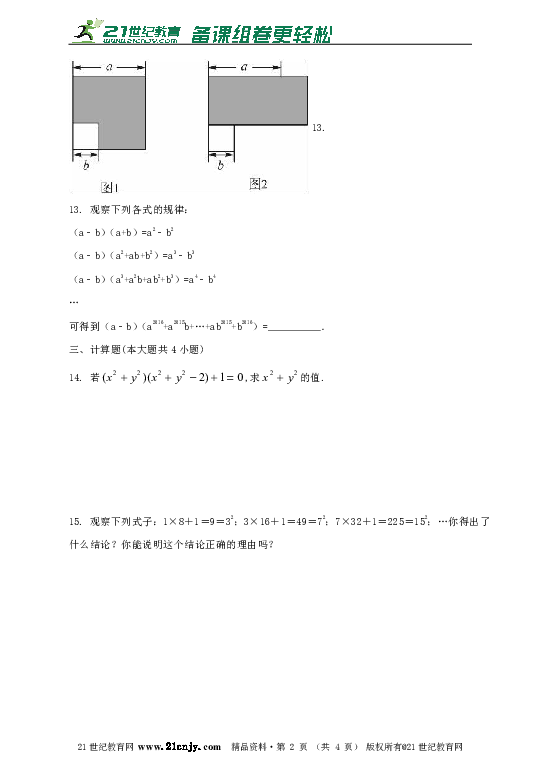
12. 如图,边长为a的正方形中有一个边长为b的小正方形,若将图1的阴影部分拼成一个长方形,如图2,比较图1和图2的阴影部分的面积,你能得到的公式是______.
13.
13. 观察下列各式的规律:
(a﹣b)(a+b)=a2﹣b2
(a﹣b)(a2+ab+b2)=a3﹣b3
(a﹣b)(a3+a2b+ab2+b3)=a4﹣b4
…
可得到(a﹣b)(a2016+a2015b+…+ab2015+b2016)= .
三、计算题(本大题共4小题)
14. 若,求的值.
15. 观察下列式子:1×8+1=9=32;3×16+1=49=72;7×32+1=225=152;…你得出了什么结论?你能说明这个结论正确的理由吗?【来源:21cnj*y.co*m】
16. 把一个边长为a米的正方形广场的四角处各留出一个边长为b(b<a)米的正方形用来修花坛,其余地方种草,问草坪的面积有多大?如果修建每平方米的草坪需要5元,请计算当a=92,b=4时,投资修此草坪需要多少钱?www-2-1-cnjy-com
17. 已知a2+b2+8a-6b+25=0,求(a+b)2 014的值.
18. 下面是某同学对多项式(a2-4a+2)(a2-4a+6)+4进行因式分解的过程.
解:设a2-4a=y
原式=(y+2)(y+6)+4(第一步)
=y2+8y+16(第二步)
=(y+4)2(第三步)
= (a2-4a+4)2(第四步)
请问:(1)该同学因式分解的结果是否彻底?________(填“彻底”或“不彻底”);
(2)若不彻底,请直接写出因式分解的最后结果________;
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
分析:根据因式分解的要求利用整体代替法解答简易。
参考答案:
一、选择题(本大题共8小题)
1. A
分析:直接利用平方差公式分解因式得出答案.
解:16﹣x2=(4﹣x)(4+x).
故选:A.
2. D
分析:利用平方差因式分解的方法.
解:A.a2+(-b)2=a2+b2,不能分解因式; B.5m2-20mn =5m(m-4n),用的是提公因式法,不是平方差公式;C.-x2-y2 =-(x2+y2),不能应用平方差公式; D.-x2+9=(3+x)(3-x),用的是平方差公式;故选D.21世纪教育网版权所有
3. D
分析:这里首末两项是x和4这两个数的平方,那么中间一项为加上或减去x和4积的2倍,故2(m-3)=±8,m=7或-1.21教育网
解:∵(x±4)2=x2±8x+16=x2+2(m-3)x+16,
∴2(m-3)=±8,
∴m=7或-1.故选D.
4. B
分析:根据因式分解是整式乘法的逆运算来解答即可.
解:= .故选B
5. D
分析:根据完全平方公式和平方差公式的结构特点,对各选项分析判断后利用排除法求解. 解:A、应为x3-x=x(x2-1)= x(x-1)(x+1),故本选项错误;21cnjy.com
B、应为x2-y2=(x-y)(x+y),故本选项错误;
C、应为-4x2+9y2=(2x+3y)(-2x+3y),故本选项错误;
D、x2+6x+9=(x+3) 2,是完全平方公式,正确;故选D.
6. B
分析:提取公因式99,计算后直接选取答案.
解:57×99+44×99-99,
=99×(57+44-1),(提公因式法)
=99×100,
=9 900.故选B.
7.B
分析:根据平方差公式计算解答即可。
解:由(x2+4)(x+2)(x-▲)得出▲=2,
则(x2+4)(x+2)(x-2)=(x2+4)(x2-4)=x4-16,则■=16.
故选B.
8. A
分析:首先提取公因式a,进而利用十字相乘法分解因式得出即可.
解: ax2﹣4ax﹣12a
=a(x2﹣4x﹣12)
=a(x﹣6)(x+2).故选A
二、填空题(本大题共5小题)
9.分析:原式利用完全平方公式及其绝对值的非负性来解答即可.
解:由已知可得,则=-2,= 3,a+b=1 .
10.分析:首先提取公因式9a,进而利用平方差公式法分解因式得出即可.
解:9a3﹣ab2
=a(9a2﹣b2)
=a(3a+b)(3a﹣b).
故答案为:a(3a+b)(3a﹣b).
11.分析:先利用多项式的乘法运算法则展开,合并同类项后再利用平方差公式分解因式即可.
解:(m+1)(m﹣9)+8m,
=m2﹣9m+m﹣9+8m,
=m2﹣9,
=(m+3)(m﹣3).
故答案为:(m+3)(m﹣3).
12. 13.
分析:根据题意分别求得图1与图2中阴影部分的面积,由两图形阴影面积相等,即可求得答案. 解:根据题意得: 图1中阴影部分的面积为:a2-b2; 图2中阴影部分的面积为:(a+b)(a-b). ∵两图形阴影面积相等, ∴可以得到的结论是:a2-b2=(a+b)(a-b). 故答案为:a2-b2=(a+b)(a-b).21·cn·jy·com
13. 观察下列各式的规律:
(a﹣b)(a+b)=a2﹣b2
(a﹣b)(a2+ab+b2)=a3﹣b3
(a﹣b)(a3+a2b+ab2+b3)=a4﹣b4
…
可得到(a﹣b)(a2016+a2015b+…+ab2015+b2016)= .
分析:根据已知等式,归纳总结得到一般性规律,写出所求式子结果即可.
解:(a﹣b)(a+b)=a2﹣b2;
(a﹣b)(a2+ab+b2)=a3﹣b3;
(a﹣b)(a3+a2b+ab2+b3)=a4﹣b4;
…
可得到(a﹣b)(a2016+a2015b+…+ab2015+b2016)=a2017﹣b2017,www.21-cn-jy.com
故答案为:a2017﹣b2017
三、计算题(本大题共4小题)
14. 分析:把(x2+y2)(x2+y2-2)+1化成(x2+y2)2-2(x2+y2)+1的形式,然后运用完全平方公式因式分解即可知答案.【来源:21·世纪·教育·网】
解:由已知得:
(x2+y2)2-2(x2+y2)+1=0
[(x2+y2)-1]2=0(完全平方公式)
∴x2+y2=1(只有0的平方为0)
15.分析:式子可以整理为:(21-1)×21+2+1=(22-1)2;
(22-1)×22+2+1=(23-1)2;
(23-1)×23+2+1=(24-1)2;
…
得到第n个式子的结论即可.
解: (2n-1)·2n+2+1=(2n+1-1)2.(2n-1)·2n+2+1=22n+2-2n+2+1=(2n+1)2-2×2n+1+1=(2n+1-1)2. 21·世纪*教育网
16.解:草坪的面积为a2-4b2(平方米).
当a=92,b=4时,草坪的面积为a2-4b2=(a+2b)(a-2b)=(92+8)×(92-8)=8 400(平方米).2-1-c-n-j-y
所以投资修此草坪需要的钱是8 400×5=42 000(元).
17. 已知a2+b2+8a-6b+25=0,求(a+b)2 014的值.
分析:对已知条件进行组合因式分解可得a、b的值,从而代入即可得到答案.
解:因为a2+b2+8a-6b+25=0,
所以(a2+8a+16)+(b2-6b+9)=0,(a+4)2+(b-3)2=0.
所以a=-4,b=3,(a+b)2 014=(-4+3)2 014=1.
18. 解:(1)不彻底
(2)(a-2)4
(3)设x2-2x=y,原式=y(y+2)+1=y2+2y+1=(y+1)2=(x2-2x+1)2=(x-1)4.
一、选择题(本大题共8小题)
1. 分解因式:16﹣x2=( )
A.(4﹣x)(4+x) B.(x﹣4)(x+4) C.(8+x)(8﹣x) D.(4﹣x)2
2. 下列多项式能用平方差公式因式分解的是( )
A. a2+(-b) 2; B. 5m2-20mn; C. -x2-y2; D. -x2+9;21*cnjy*com
3. 若x2+2(m-3)+16是完全平方式,则m的值为( )
A. -5; B. 7; C. -1; D. 7或-1;
4. 一个多项式分解因式的结果是,那么这个多项式是( )
A. B. C. D.
5. 下列因式分解正确的是( )
A.x3-x=x(x-1) B.x2-y2=(x-y)2
C.-4x2+9y2=(2x+3y)(2x-3y) D.x2+6x+9=(x+3) 2
6. 利用因式分解简便计算57×99+44×99-99正确的是( )
A.99×(57+44)=9 999 B.99×(57+44-1)=9 900
C.99×(57+44+1)=10 098 D.99×(57+44-99)=198
7. 某同学粗心大意,因式分解时,把等式x4-■=(x2+4)(x+2)(x-▲)中的两个数弄污了,则式子中的■,▲对应得一组数可以是( )2·1·c·n·j·y
A. 8,1; B.16,2; C.24,3; D. 64,8;
8. 多项式ax2﹣4ax﹣12a因式分解正确的是( )
A.a(x﹣6)(x+2) B.a(x﹣3)(x+4)C.a(x2﹣4x﹣12)D. a(x+6)(x﹣2)
二、填空题(本大题共5小题)
9. 已知,则= .
10. 把多项式9a3﹣ab2分解因式的结果是 .
11. 分解因式:(m+1)(m﹣9)+8m= .
12. 如图,边长为a的正方形中有一个边长为b的小正方形,若将图1的阴影部分拼成一个长方形,如图2,比较图1和图2的阴影部分的面积,你能得到的公式是______.
13.
13. 观察下列各式的规律:
(a﹣b)(a+b)=a2﹣b2
(a﹣b)(a2+ab+b2)=a3﹣b3
(a﹣b)(a3+a2b+ab2+b3)=a4﹣b4
…
可得到(a﹣b)(a2016+a2015b+…+ab2015+b2016)= .
三、计算题(本大题共4小题)
14. 若,求的值.
15. 观察下列式子:1×8+1=9=32;3×16+1=49=72;7×32+1=225=152;…你得出了什么结论?你能说明这个结论正确的理由吗?【来源:21cnj*y.co*m】
16. 把一个边长为a米的正方形广场的四角处各留出一个边长为b(b<a)米的正方形用来修花坛,其余地方种草,问草坪的面积有多大?如果修建每平方米的草坪需要5元,请计算当a=92,b=4时,投资修此草坪需要多少钱?www-2-1-cnjy-com
17. 已知a2+b2+8a-6b+25=0,求(a+b)2 014的值.
18. 下面是某同学对多项式(a2-4a+2)(a2-4a+6)+4进行因式分解的过程.
解:设a2-4a=y
原式=(y+2)(y+6)+4(第一步)
=y2+8y+16(第二步)
=(y+4)2(第三步)
= (a2-4a+4)2(第四步)
请问:(1)该同学因式分解的结果是否彻底?________(填“彻底”或“不彻底”);
(2)若不彻底,请直接写出因式分解的最后结果________;
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
分析:根据因式分解的要求利用整体代替法解答简易。
参考答案:
一、选择题(本大题共8小题)
1. A
分析:直接利用平方差公式分解因式得出答案.
解:16﹣x2=(4﹣x)(4+x).
故选:A.
2. D
分析:利用平方差因式分解的方法.
解:A.a2+(-b)2=a2+b2,不能分解因式; B.5m2-20mn =5m(m-4n),用的是提公因式法,不是平方差公式;C.-x2-y2 =-(x2+y2),不能应用平方差公式; D.-x2+9=(3+x)(3-x),用的是平方差公式;故选D.21世纪教育网版权所有
3. D
分析:这里首末两项是x和4这两个数的平方,那么中间一项为加上或减去x和4积的2倍,故2(m-3)=±8,m=7或-1.21教育网
解:∵(x±4)2=x2±8x+16=x2+2(m-3)x+16,
∴2(m-3)=±8,
∴m=7或-1.故选D.
4. B
分析:根据因式分解是整式乘法的逆运算来解答即可.
解:= .故选B
5. D
分析:根据完全平方公式和平方差公式的结构特点,对各选项分析判断后利用排除法求解. 解:A、应为x3-x=x(x2-1)= x(x-1)(x+1),故本选项错误;21cnjy.com
B、应为x2-y2=(x-y)(x+y),故本选项错误;
C、应为-4x2+9y2=(2x+3y)(-2x+3y),故本选项错误;
D、x2+6x+9=(x+3) 2,是完全平方公式,正确;故选D.
6. B
分析:提取公因式99,计算后直接选取答案.
解:57×99+44×99-99,
=99×(57+44-1),(提公因式法)
=99×100,
=9 900.故选B.
7.B
分析:根据平方差公式计算解答即可。
解:由(x2+4)(x+2)(x-▲)得出▲=2,
则(x2+4)(x+2)(x-2)=(x2+4)(x2-4)=x4-16,则■=16.
故选B.
8. A
分析:首先提取公因式a,进而利用十字相乘法分解因式得出即可.
解: ax2﹣4ax﹣12a
=a(x2﹣4x﹣12)
=a(x﹣6)(x+2).故选A
二、填空题(本大题共5小题)
9.分析:原式利用完全平方公式及其绝对值的非负性来解答即可.
解:由已知可得,则=-2,= 3,a+b=1 .
10.分析:首先提取公因式9a,进而利用平方差公式法分解因式得出即可.
解:9a3﹣ab2
=a(9a2﹣b2)
=a(3a+b)(3a﹣b).
故答案为:a(3a+b)(3a﹣b).
11.分析:先利用多项式的乘法运算法则展开,合并同类项后再利用平方差公式分解因式即可.
解:(m+1)(m﹣9)+8m,
=m2﹣9m+m﹣9+8m,
=m2﹣9,
=(m+3)(m﹣3).
故答案为:(m+3)(m﹣3).
12. 13.
分析:根据题意分别求得图1与图2中阴影部分的面积,由两图形阴影面积相等,即可求得答案. 解:根据题意得: 图1中阴影部分的面积为:a2-b2; 图2中阴影部分的面积为:(a+b)(a-b). ∵两图形阴影面积相等, ∴可以得到的结论是:a2-b2=(a+b)(a-b). 故答案为:a2-b2=(a+b)(a-b).21·cn·jy·com
13. 观察下列各式的规律:
(a﹣b)(a+b)=a2﹣b2
(a﹣b)(a2+ab+b2)=a3﹣b3
(a﹣b)(a3+a2b+ab2+b3)=a4﹣b4
…
可得到(a﹣b)(a2016+a2015b+…+ab2015+b2016)= .
分析:根据已知等式,归纳总结得到一般性规律,写出所求式子结果即可.
解:(a﹣b)(a+b)=a2﹣b2;
(a﹣b)(a2+ab+b2)=a3﹣b3;
(a﹣b)(a3+a2b+ab2+b3)=a4﹣b4;
…
可得到(a﹣b)(a2016+a2015b+…+ab2015+b2016)=a2017﹣b2017,www.21-cn-jy.com
故答案为:a2017﹣b2017
三、计算题(本大题共4小题)
14. 分析:把(x2+y2)(x2+y2-2)+1化成(x2+y2)2-2(x2+y2)+1的形式,然后运用完全平方公式因式分解即可知答案.【来源:21·世纪·教育·网】
解:由已知得:
(x2+y2)2-2(x2+y2)+1=0
[(x2+y2)-1]2=0(完全平方公式)
∴x2+y2=1(只有0的平方为0)
15.分析:式子可以整理为:(21-1)×21+2+1=(22-1)2;
(22-1)×22+2+1=(23-1)2;
(23-1)×23+2+1=(24-1)2;
…
得到第n个式子的结论即可.
解: (2n-1)·2n+2+1=(2n+1-1)2.(2n-1)·2n+2+1=22n+2-2n+2+1=(2n+1)2-2×2n+1+1=(2n+1-1)2. 21·世纪*教育网
16.解:草坪的面积为a2-4b2(平方米).
当a=92,b=4时,草坪的面积为a2-4b2=(a+2b)(a-2b)=(92+8)×(92-8)=8 400(平方米).2-1-c-n-j-y
所以投资修此草坪需要的钱是8 400×5=42 000(元).
17. 已知a2+b2+8a-6b+25=0,求(a+b)2 014的值.
分析:对已知条件进行组合因式分解可得a、b的值,从而代入即可得到答案.
解:因为a2+b2+8a-6b+25=0,
所以(a2+8a+16)+(b2-6b+9)=0,(a+4)2+(b-3)2=0.
所以a=-4,b=3,(a+b)2 014=(-4+3)2 014=1.
18. 解:(1)不彻底
(2)(a-2)4
(3)设x2-2x=y,原式=y(y+2)+1=y2+2y+1=(y+1)2=(x2-2x+1)2=(x-1)4.
