1.2 简单的逻辑联结词
图片预览




文档简介
课件26张PPT。第1章 常用逻辑用语1.2 简单的逻辑联结词1.了解联结词“且”“或”“非”的含义.
2.会用联结词“且”“或”“非”联结或改写某些数学命题,并判断新命题的真假.
3.通过学习,明白对条件的判定应该归结为判断命题的真假.学习目标知识梳理 自主学习题型探究 重点突破当堂检测 自查自纠栏目索引 知识梳理 自主学习知识点一 “p且q”答案 “p且q”就是用联结词“ ”把命题p和命题q联结起来,得到的新命题,
记作 .p∧qp∨q且或知识点二 “p或q” “p或q”就是用联结词“ ”把命题p和命题q联结起来,得到的新命题,
记作 .知识点三 命题的否定一般地,对一个命题p ,就得到一个新命题,记作非p,读作
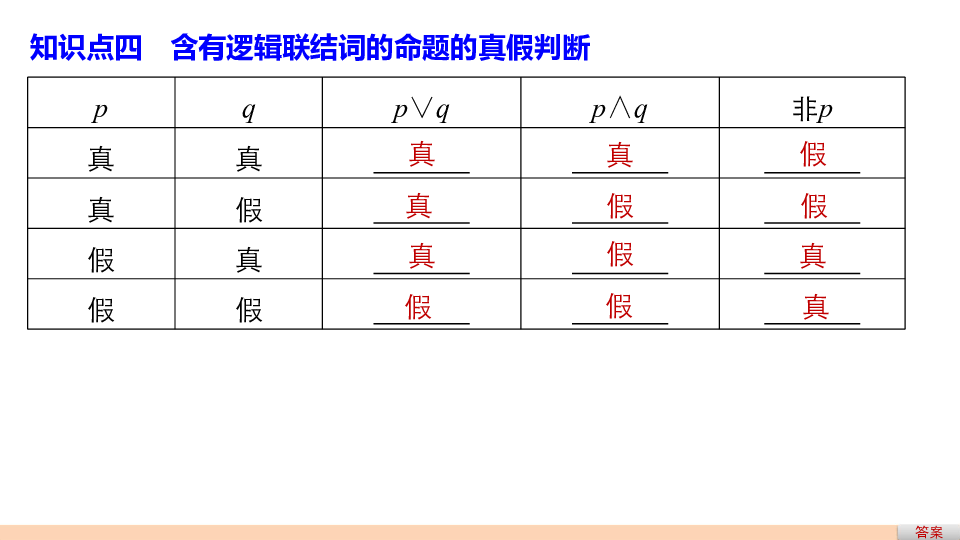
“ ”或“ ”.全盘否定非pp的否定答案知识点四 含有逻辑联结词的命题的真假判断真真真假真假假假假假真真思考 (1)逻辑联结词“或”与生活用语中的“或”的含义是否相同?答案答案 生活用语中的“或”表示不兼有,而在数学中所研究的“或”则表示可兼有但不一定必须兼有.(2)命题的否定与否命题有什么区别?答案 命题的否定只否定命题的结论,而否命题既否定命题的条件,又否定命题的结论.返回例1 分别写出下列命题构成的“p∧q”“p∨q”的形式,并判断它们的真假.
(1)p:函数y=3x2是偶函数,q:函数y=3x2是增函数; 题型探究 重点突破题型一 p∧q命题及p∨q命题解 p∧q:函数y=3x2是偶函数且是增函数;
∵p真,q假,∴p∧q为假.
p∨q:函数y=3x2是偶函数或是增函数;
∵p真,q假,∴p∨q为真.解析答案(2)p:三角形的外角等于与它不相邻的两个内角的和,q:三角形的外角大于与它不相邻的任何一个内角;解 p∧q:三角形的外角等于与它不相邻的两个内角的和且大于与它不相邻的任何一个内角;
∵p真,q真,∴p∧q为真.
p∨q:三角形的外角等于与它不相邻的两个内角的和或大于与它不相邻的任何一个内角;
∵p真,q真,∴p∨q为真.解析答案∵p真,q真,∴p∧q为真.解析答案反思与感悟∵p真,q真,∴p∨q为真.(4)p:方程x2+2x+1=0有两个相等的实数根,q:方程x2+2x+1=0两根的绝对值相等.解 p∧q:方程x2+2x+1=0有两个相等的实数根且两根的绝对值相等;
∵p真,q真,∴p∧q为真.
p∨q:方程x2+2x+1=0有两个相等的实数根或两根的绝对值相等;
∵p真,q真,∴p∨q为真.(1)判断p∧q形式的命题的真假,首先判断命题p与命题q的真假,然后根据真值表“一假则假,全真则真”进行判断.
(2)判断p∨q形式的命题的真假,首先判断命题p与命题q的真假,只要有一个为真,即可判定p∨q形式命题为真,而p与q均为假命题时,命题p∨q为假命题,可简记为:有真则真,全假为假.反思与感悟跟踪训练1 指出下列命题的构成形式及构成它们的简单命题:
(1)李明是男生且是高一学生.解析答案解 是“p且q”形式.
其中p:李明是男生;q:李明是高一学生.(2)方程2x2+1=0没有实数根.解 是“非p”形式.其中p:方程2x2+1=0有实根.(3)12能被3或4整除.解 是“p或q”形式.其中p:12能被3整除;q:12能被4整除.例2 写出下列命题的否定形式.
(1)面积相等的三角形都是全等三角形;题型二 非p命题解析答案反思与感悟解 面积相等的三角形不都是全等三角形.(2)若m2+n2=0,则实数m、n全为零;解 若m2+n2=0,则实数m、n不全为零.(3)若xy=0,则x=0或y=0.解 若xy=0,则x≠0且y≠0.非p是对命题p的全盘否定,对一些词语的正确否定是写非p的关键,如“都”的否定是“不都”,“至多两个”的反面是“至少三个”、“p∧q”的否定是“非p∨非q”等.反思与感悟跟踪训练2 写出下列命题的否定,并判断其真假.
(1)p:y = sin x 是周期函数;解 非p:y = sin x不是周期函数.命题p是真命题,非p是假命题;解析答案(2)p:3<2;解 非p:3≥2.命题p是假命题,非p是真命题;(3)p:空集是集合A的子集;解 非p:空集不是集合A的子集.命题p是真命题,非p是假命题;(4)p:5不是75的约数.解 非p:5是75的约数.命题p是假命题,非p是真命题.例3 已知命题p:方程x2+2ax+1=0有两个大于-1的实数根,命题q:关于x的不等式ax2-ax+1>0的解集为R,若“p∨q”与“非q”同时为真命题,求实数a的取值范围.题型三 p∨q、p∧ q 、非p命题的综合应用解析答案反思与感悟反思与感悟解 命题p:方程x2+2ax+1=0有两个大于-1的实数根,等价于命题q:关于x的不等式ax2-ax+1>0的解集为R,等价于a=0或所以0≤a<4.因为“p∨q”与“非q”同时为真命题,即p真且q假,故实数a的取值范围是(-∞,-1].由真值表可判断p∨q、p∧q、非p命题的真假,反之,由p∨q,p∧q,非p命题的真假也可判断p、q的真假情况.一般求满足p假成立的参数范围,应先求p真成立的参数的范围,再求其补集.反思与感悟跟踪训练3 已知命题p:方程x2+ax+1=0有两个不等的实根;命题q:方程4x2+2(a-4)x+1=0无实根,若“p或q”为真,“p且q”为假,求实数a的取值范围.解析答案解 ∵“p或q”为真,“p且q”为假,∴p与q一真一假,
由a2-4>0得a>2或a<-2.
由4(a-4)2-4×4<0得20”是“x2>0”的必要不充分条件,命题q:△ABC中,“A>B”是“sin A>sin B”的充要条件,则下列四个命题正确的是________.(填序号)
①p真q假 ②p∧q为真
③p∨q为假 ④p假q真解析答案解析 命题p假,命题q真.④123452.给出下列命题:
①2>1或1>3;
②方程x2-2x-4=0的判别式大于或等于0;
③25是6或5的倍数;
④集合A∩B是A的子集,且是A∪B的子集.
其中真命题的个数为________.解析答案12345解析 ①由于2>1是真命题,所以“2>1或1>3”是真命题;
②由于方程x2-2x-4=0的Δ=4+16>0,所以“方程x2-2x-4=0的判别式大于或等于0”是真命题;
③由于25是5的倍数,所以命题“25是6或5的倍数”是真命题;
④由于A∩B?A,A∩B?A∪B,所以命题“集合A∩B是A的子集,且是A∪B的子集”是真命题.答案 4123453.已知命题p1:函数y=2x-2-x在R上为增函数,
p2:函数y=2x+2-x在R上为减函数.
则在命题①p1∨p2,②p1∧p2,③(非p1)∨p2和④p1∧(非p2)中,为真命题的是________.解析 p1是真命题,则非p1为假命题;p2是假命题,则非p2为真命题;
∴①p1∨p2是真命题,②p1∧p2是假命题,
∴③(非p1)∨p2为假命题,④p1∧(非p2)为真命题.
∴为真命题的是①④.①④解析答案123454.已知命题p:1∈{x|(x+2)(x-3)<0},命题q:?={0},则下列判断正确的是________.
①p假q真 ②“p∨q”为真
③“p∧q”为真 ④“非p”为真解析 由(x+2)(x-3)<0得-2∵1∈(-2,3),∴p真.
∵?≠{0},∴q为假,
∴“p∨q”为真.②解析答案12345解析答案①p为真 ② 非 p为假 ③p∧q为假 ④p∨q为真③课堂小结1.正确理解逻辑联结词是解题的关键,日常用语中的“或”是两个中任选一个,不能都选,而逻辑联结词中的“或”是两个中至少选一个.
2.判断含逻辑联结词的命题的真假的步骤:
(1)逐一判断命题p,q的真假.
(2)根据“且”“或”的含义判断“p∧q”,“p∨q”的真假.
p∧q为真?p和q同时为真,
p∨q为真?p和q中至少一个为真.返回3.若命题p为真,则“非p”为假;若p为假,则“非p”为真,类比集合知识,“非p”就相当于集合p在全集U中的补集?Up.因此(非p)∧p为假,(非p)∨p为真.
4.命题的否定只否定结论,否命题既否定结论又否定条件,要注意区别.
2.会用联结词“且”“或”“非”联结或改写某些数学命题,并判断新命题的真假.
3.通过学习,明白对条件的判定应该归结为判断命题的真假.学习目标知识梳理 自主学习题型探究 重点突破当堂检测 自查自纠栏目索引 知识梳理 自主学习知识点一 “p且q”答案 “p且q”就是用联结词“ ”把命题p和命题q联结起来,得到的新命题,
记作 .p∧qp∨q且或知识点二 “p或q” “p或q”就是用联结词“ ”把命题p和命题q联结起来,得到的新命题,
记作 .知识点三 命题的否定一般地,对一个命题p ,就得到一个新命题,记作非p,读作
“ ”或“ ”.全盘否定非pp的否定答案知识点四 含有逻辑联结词的命题的真假判断真真真假真假假假假假真真思考 (1)逻辑联结词“或”与生活用语中的“或”的含义是否相同?答案答案 生活用语中的“或”表示不兼有,而在数学中所研究的“或”则表示可兼有但不一定必须兼有.(2)命题的否定与否命题有什么区别?答案 命题的否定只否定命题的结论,而否命题既否定命题的条件,又否定命题的结论.返回例1 分别写出下列命题构成的“p∧q”“p∨q”的形式,并判断它们的真假.
(1)p:函数y=3x2是偶函数,q:函数y=3x2是增函数; 题型探究 重点突破题型一 p∧q命题及p∨q命题解 p∧q:函数y=3x2是偶函数且是增函数;
∵p真,q假,∴p∧q为假.
p∨q:函数y=3x2是偶函数或是增函数;
∵p真,q假,∴p∨q为真.解析答案(2)p:三角形的外角等于与它不相邻的两个内角的和,q:三角形的外角大于与它不相邻的任何一个内角;解 p∧q:三角形的外角等于与它不相邻的两个内角的和且大于与它不相邻的任何一个内角;
∵p真,q真,∴p∧q为真.
p∨q:三角形的外角等于与它不相邻的两个内角的和或大于与它不相邻的任何一个内角;
∵p真,q真,∴p∨q为真.解析答案∵p真,q真,∴p∧q为真.解析答案反思与感悟∵p真,q真,∴p∨q为真.(4)p:方程x2+2x+1=0有两个相等的实数根,q:方程x2+2x+1=0两根的绝对值相等.解 p∧q:方程x2+2x+1=0有两个相等的实数根且两根的绝对值相等;
∵p真,q真,∴p∧q为真.
p∨q:方程x2+2x+1=0有两个相等的实数根或两根的绝对值相等;
∵p真,q真,∴p∨q为真.(1)判断p∧q形式的命题的真假,首先判断命题p与命题q的真假,然后根据真值表“一假则假,全真则真”进行判断.
(2)判断p∨q形式的命题的真假,首先判断命题p与命题q的真假,只要有一个为真,即可判定p∨q形式命题为真,而p与q均为假命题时,命题p∨q为假命题,可简记为:有真则真,全假为假.反思与感悟跟踪训练1 指出下列命题的构成形式及构成它们的简单命题:
(1)李明是男生且是高一学生.解析答案解 是“p且q”形式.
其中p:李明是男生;q:李明是高一学生.(2)方程2x2+1=0没有实数根.解 是“非p”形式.其中p:方程2x2+1=0有实根.(3)12能被3或4整除.解 是“p或q”形式.其中p:12能被3整除;q:12能被4整除.例2 写出下列命题的否定形式.
(1)面积相等的三角形都是全等三角形;题型二 非p命题解析答案反思与感悟解 面积相等的三角形不都是全等三角形.(2)若m2+n2=0,则实数m、n全为零;解 若m2+n2=0,则实数m、n不全为零.(3)若xy=0,则x=0或y=0.解 若xy=0,则x≠0且y≠0.非p是对命题p的全盘否定,对一些词语的正确否定是写非p的关键,如“都”的否定是“不都”,“至多两个”的反面是“至少三个”、“p∧q”的否定是“非p∨非q”等.反思与感悟跟踪训练2 写出下列命题的否定,并判断其真假.
(1)p:y = sin x 是周期函数;解 非p:y = sin x不是周期函数.命题p是真命题,非p是假命题;解析答案(2)p:3<2;解 非p:3≥2.命题p是假命题,非p是真命题;(3)p:空集是集合A的子集;解 非p:空集不是集合A的子集.命题p是真命题,非p是假命题;(4)p:5不是75的约数.解 非p:5是75的约数.命题p是假命题,非p是真命题.例3 已知命题p:方程x2+2ax+1=0有两个大于-1的实数根,命题q:关于x的不等式ax2-ax+1>0的解集为R,若“p∨q”与“非q”同时为真命题,求实数a的取值范围.题型三 p∨q、p∧ q 、非p命题的综合应用解析答案反思与感悟反思与感悟解 命题p:方程x2+2ax+1=0有两个大于-1的实数根,等价于命题q:关于x的不等式ax2-ax+1>0的解集为R,等价于a=0或所以0≤a<4.因为“p∨q”与“非q”同时为真命题,即p真且q假,故实数a的取值范围是(-∞,-1].由真值表可判断p∨q、p∧q、非p命题的真假,反之,由p∨q,p∧q,非p命题的真假也可判断p、q的真假情况.一般求满足p假成立的参数范围,应先求p真成立的参数的范围,再求其补集.反思与感悟跟踪训练3 已知命题p:方程x2+ax+1=0有两个不等的实根;命题q:方程4x2+2(a-4)x+1=0无实根,若“p或q”为真,“p且q”为假,求实数a的取值范围.解析答案解 ∵“p或q”为真,“p且q”为假,∴p与q一真一假,
由a2-4>0得a>2或a<-2.
由4(a-4)2-4×4<0得2
①p真q假 ②p∧q为真
③p∨q为假 ④p假q真解析答案解析 命题p假,命题q真.④123452.给出下列命题:
①2>1或1>3;
②方程x2-2x-4=0的判别式大于或等于0;
③25是6或5的倍数;
④集合A∩B是A的子集,且是A∪B的子集.
其中真命题的个数为________.解析答案12345解析 ①由于2>1是真命题,所以“2>1或1>3”是真命题;
②由于方程x2-2x-4=0的Δ=4+16>0,所以“方程x2-2x-4=0的判别式大于或等于0”是真命题;
③由于25是5的倍数,所以命题“25是6或5的倍数”是真命题;
④由于A∩B?A,A∩B?A∪B,所以命题“集合A∩B是A的子集,且是A∪B的子集”是真命题.答案 4123453.已知命题p1:函数y=2x-2-x在R上为增函数,
p2:函数y=2x+2-x在R上为减函数.
则在命题①p1∨p2,②p1∧p2,③(非p1)∨p2和④p1∧(非p2)中,为真命题的是________.解析 p1是真命题,则非p1为假命题;p2是假命题,则非p2为真命题;
∴①p1∨p2是真命题,②p1∧p2是假命题,
∴③(非p1)∨p2为假命题,④p1∧(非p2)为真命题.
∴为真命题的是①④.①④解析答案123454.已知命题p:1∈{x|(x+2)(x-3)<0},命题q:?={0},则下列判断正确的是________.
①p假q真 ②“p∨q”为真
③“p∧q”为真 ④“非p”为真解析 由(x+2)(x-3)<0得-2
∵?≠{0},∴q为假,
∴“p∨q”为真.②解析答案12345解析答案①p为真 ② 非 p为假 ③p∧q为假 ④p∨q为真③课堂小结1.正确理解逻辑联结词是解题的关键,日常用语中的“或”是两个中任选一个,不能都选,而逻辑联结词中的“或”是两个中至少选一个.
2.判断含逻辑联结词的命题的真假的步骤:
(1)逐一判断命题p,q的真假.
(2)根据“且”“或”的含义判断“p∧q”,“p∨q”的真假.
p∧q为真?p和q同时为真,
p∨q为真?p和q中至少一个为真.返回3.若命题p为真,则“非p”为假;若p为假,则“非p”为真,类比集合知识,“非p”就相当于集合p在全集U中的补集?Up.因此(非p)∧p为假,(非p)∨p为真.
4.命题的否定只否定结论,否命题既否定结论又否定条件,要注意区别.
