第2章 圆锥曲线与方程 章末复习提升
图片预览




文档简介
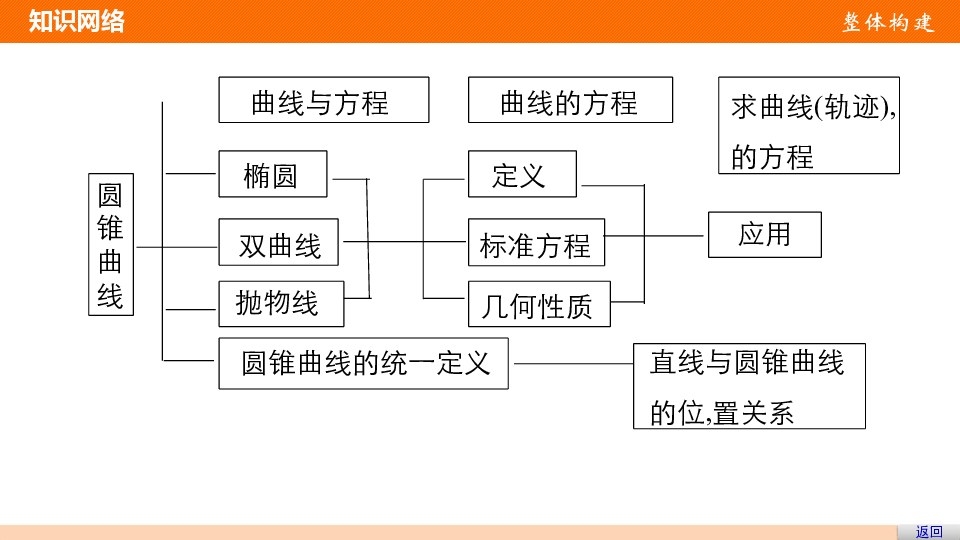
课件33张PPT。第2章 圆锥曲线与方程章末复习提升栏目索引知识网络 整体构建要点归纳 主干梳理方法总结 思想构建返回圆
锥
曲
线双曲线标准方程应用定义几何性质椭圆曲线与方程曲线的方程求曲线(轨迹),
的方程抛物线圆锥曲线的统一定义直线与圆锥曲线
的位,置关系 知识网络 整体构建1.椭圆、双曲线、抛物线的定义、标准方程、几何性质 要点归纳 主干梳理2.曲线与方程
(1)曲线与方程:如果曲线C上的点与一个二元方程的实数解建立了如下的关系:①曲线上点的坐标都是这个方程的解;②以这个方程的解为坐标的点都在曲线上,那么,这条曲线叫做方程的曲线,这个方程叫做曲线的方程.
(2)圆锥曲线的共同特征:圆锥曲线上的点到一个定点的距离与它到一条定直线的距离之比是定值e;当01时,圆锥曲线是双曲线;当e=1时,圆锥曲线是抛物线.
返回3.直线与圆锥曲线的位置关系
直线和圆锥曲线的位置关系有三种:相离、相切、相交.设直线l的方程为Ax+By+C=0,与圆锥曲线D的方程联立可得(消去y)ax2+bx+c=0(*).
(1)当a≠0时,若关于x的方程(*)的判别式Δ>0,则直线与圆锥曲线有两个不同交点;若Δ<0,则直线与圆锥曲线没有交点;若Δ=0,则直线与圆锥曲线相切.
(2)当a=0时,若方程(*)有解,则直线与圆锥曲线有一个交点.1.数形结合思想“数形结合”指的是在处理数学问题时,能够将抽象的数学语言与直观的几何图形有机结合起来思索,促使抽象思维和形象思维的和谐结合,通过对规范图形或示意图形的观察分析,化抽象为直观,化直观为精确,从而使问题得到解决.判断直线与圆锥曲线的位置关系、求最值等问题,可以结合图形,运用数形结合思想,化抽象为具体,使问题变得简单.
方法总结 思想构建 解析答案解析 如图所示, 由PF1=2PF2知P在双曲线的右支上,解析答案则PF1-PF2=2a,
又PF1=2PF2,
∴PF1=4a,PF2=2a,
在△F1PF2中,由余弦定理得∵0<∠F1PF2≤π,
且当点P是双曲线的顶点时,∠F1PF2=π,
∴-1≤cos∠F1PF2<1,答案 (1,3]解析答案跟踪训练1 抛物线y2=2px(p>0)上有A(x1,y1),B(x2,y2),C(x3,y3)三点,F是它的焦点,若AF,BF,CF成等差数列,则下列说法正确的是________.
①x1,x2,x3成等差数列
②y1,y2,y3成等差数列
③x1,x3,x2成等差数列
④y1,y3,y2成等差数列解析 如图,过A,B,C分别作准线的垂线,垂足分别为A′,B′,C′,由抛物线定义知:AF=AA′,BF=BB′,CF=CC′.
∵2BF=AF+CF,
∴2BB′=AA′+CC′.答案 ①分类讨论思想是指当所给的对象不能进行统一研究时,我们就需要对研究的对象进行分类,然后对每一类进行研究,得出每一类的结论,最后综合各类的结果得到整个问题的结果.如曲线方程中含有的参数的取值范围不同,对应的曲线也不同,这时要讨论字母的取值范围,有时焦点位置也要讨论,直线的斜率是否存在也需要讨论.2.分类讨论思想解析答案解析答案跟踪训练2 求适合下列条件的椭圆的标准方程.
(1)椭圆的长轴长是短轴长的2倍,且过点P(2,-6);由已知得a=2b. ①由①②得a2=148,b2=37或a2=52,b2=13.解 当焦点在x轴上时,∵椭圆过点P(3,0),∴a=3.∴b2=a2-c2=3.当焦点在y轴上时,∵椭圆过点P(3,0),∴b=3.解析答案圆锥曲线中的许多问题,若能运用函数与方程的思想去分析,则往往能较快地找到解题的突破口.用函数思想解决圆锥曲线中的有关定值、最值问题,最值问题是高中数学中常见的问题,在圆锥曲线问题中也不例外,而函数思想是解决最值问题最有利的武器.我们通常可用建立目标函数的方法解有关圆锥曲线的最值问题.
方程思想是从分析问题的数量关系入手,通过联想与类比,将问题中的条件转化为方程或方程组,然后通过解方程或方程组使问题获解,方程思想是高中数学中最基本、最重要的思想方法之一,在高考中占有非常重要的地位.在求圆锥曲线方程、直线与圆锥曲线的位置关系的问题中经常利用方程或方程组来解决.3.函数与方程思想解析答案例3 已知椭圆ax2+by2=1(a>0,b>0且a≠b)与直线x+y-1=0相交于A,B两点,C是AB的中点,求椭圆的方程.解 方法一 设A(x1,y1),B(x2,y2),代入椭圆方程并作差,得
a(x1+x2)(x1-x2)+b(y1+y2)(y1-y2)=0. ①直线x+y-1=0的斜率k=-1.∴|x2-x1|=2.
联立ax2+by2=1与x+y-1=0可得(a+b)x2-2bx+b-1=0.解析答案解析答案得(a+b)x2-2bx+b-1=0.设A(x1,y1),B(x2,y2),解析答案解析答案得a=3.34.化归与转化思想将所研究的对象在一定条件下转化并归结为另一种研究对象的思想方法称之为化归与转化思想.一般将有待解决的问题进行转化,使之成为大家熟悉的或容易解决的问题模式.转化与化归思想在圆锥曲线中经常应用,如把直线与圆锥曲线的位置关系问题转化为方程组的解的个数问题,把求参数的取值范围问题转化为解不等式(组)问题,把陌生的问题转化为熟悉的问题,需要注意转化的等价性.例4 已知点A(4,-2),F为抛物线y2=8x的焦点,点M在抛物线上移动,当MA+MF取最小值时,点M的坐标为________.解析答案解析 过点M作准线l的垂线,垂足为E,由抛物线定义知MF=ME.
当点M在抛物线上移动时,MF+MA的值在变化,
显然M移到M′,AM′∥Ox时,
A,M,E共线,此时ME+MA最小,解析答案(1)求点Q(x,y)的轨迹C的方程;解 由题意得,解析答案(2)设曲线C与直线y=kx+m相交于不同的两点M、N,又点A(0,-1),当AM=AN时,求实数m的取值范围.得(3k2+1)x2+6mkx+3(m2-1)=0,
由于直线与椭圆有两个不同的交点,
∴Δ>0,即m2<3k2+1. ①(ⅰ)当k≠0时,设弦MN的中点为P(xP,yP),xM、xN分别为点M、N的横坐标,解析答案又AM=AN,∴AP⊥MN.将②代入①得2m>m2,解得0∴AP⊥MN,m2<3k2+1即为m2<1,解得-12.圆锥曲线的标准方程是用代数方法研究圆锥曲线的几何性质的基础,对圆锥曲线标准方程的考查方式有两种:一是在解答题中作为试题的入口进行考查;二是在填空题中结合圆锥曲线的简单几何性质进行考查.
3.虽然考纲中没有直接要求关于直线与圆锥曲线相结合的知识,但直线与圆锥曲线是密不可分的,如双曲线的渐近线、抛物线的准线,圆锥曲线的对称轴等都是直线.考试不但不回避直线与圆锥曲线,而且在试题中进行重点考查,考查方式既可以是填空题,也可以是解答题.课堂小结4.考纲对曲线与方程的要求是“了解方程的曲线与曲线的方程的对应关系”,考试对曲线与方程的考查主要体现在以利用圆锥曲线的定义、待定系数法、直接法和代入法等方法求圆锥曲线的方程.
5.对圆锥曲线的考查是综合性的,这种综合性体现在圆锥曲线、直线、圆、平面向量、不等式等知识的相互交汇,对圆锥曲线的综合考查主要是在解答题中进行,一般以椭圆或者抛物线为依托,全面考查圆锥曲线与方程的求法、直线与圆锥曲线的位置关系,考查函数、方程、不等式、平面向量等在解决问题中的综合运用.返回
锥
曲
线双曲线标准方程应用定义几何性质椭圆曲线与方程曲线的方程求曲线(轨迹),
的方程抛物线圆锥曲线的统一定义直线与圆锥曲线
的位,置关系 知识网络 整体构建1.椭圆、双曲线、抛物线的定义、标准方程、几何性质 要点归纳 主干梳理2.曲线与方程
(1)曲线与方程:如果曲线C上的点与一个二元方程的实数解建立了如下的关系:①曲线上点的坐标都是这个方程的解;②以这个方程的解为坐标的点都在曲线上,那么,这条曲线叫做方程的曲线,这个方程叫做曲线的方程.
(2)圆锥曲线的共同特征:圆锥曲线上的点到一个定点的距离与它到一条定直线的距离之比是定值e;当0
返回3.直线与圆锥曲线的位置关系
直线和圆锥曲线的位置关系有三种:相离、相切、相交.设直线l的方程为Ax+By+C=0,与圆锥曲线D的方程联立可得(消去y)ax2+bx+c=0(*).
(1)当a≠0时,若关于x的方程(*)的判别式Δ>0,则直线与圆锥曲线有两个不同交点;若Δ<0,则直线与圆锥曲线没有交点;若Δ=0,则直线与圆锥曲线相切.
(2)当a=0时,若方程(*)有解,则直线与圆锥曲线有一个交点.1.数形结合思想“数形结合”指的是在处理数学问题时,能够将抽象的数学语言与直观的几何图形有机结合起来思索,促使抽象思维和形象思维的和谐结合,通过对规范图形或示意图形的观察分析,化抽象为直观,化直观为精确,从而使问题得到解决.判断直线与圆锥曲线的位置关系、求最值等问题,可以结合图形,运用数形结合思想,化抽象为具体,使问题变得简单.
方法总结 思想构建 解析答案解析 如图所示, 由PF1=2PF2知P在双曲线的右支上,解析答案则PF1-PF2=2a,
又PF1=2PF2,
∴PF1=4a,PF2=2a,
在△F1PF2中,由余弦定理得∵0<∠F1PF2≤π,
且当点P是双曲线的顶点时,∠F1PF2=π,
∴-1≤cos∠F1PF2<1,答案 (1,3]解析答案跟踪训练1 抛物线y2=2px(p>0)上有A(x1,y1),B(x2,y2),C(x3,y3)三点,F是它的焦点,若AF,BF,CF成等差数列,则下列说法正确的是________.
①x1,x2,x3成等差数列
②y1,y2,y3成等差数列
③x1,x3,x2成等差数列
④y1,y3,y2成等差数列解析 如图,过A,B,C分别作准线的垂线,垂足分别为A′,B′,C′,由抛物线定义知:AF=AA′,BF=BB′,CF=CC′.
∵2BF=AF+CF,
∴2BB′=AA′+CC′.答案 ①分类讨论思想是指当所给的对象不能进行统一研究时,我们就需要对研究的对象进行分类,然后对每一类进行研究,得出每一类的结论,最后综合各类的结果得到整个问题的结果.如曲线方程中含有的参数的取值范围不同,对应的曲线也不同,这时要讨论字母的取值范围,有时焦点位置也要讨论,直线的斜率是否存在也需要讨论.2.分类讨论思想解析答案解析答案跟踪训练2 求适合下列条件的椭圆的标准方程.
(1)椭圆的长轴长是短轴长的2倍,且过点P(2,-6);由已知得a=2b. ①由①②得a2=148,b2=37或a2=52,b2=13.解 当焦点在x轴上时,∵椭圆过点P(3,0),∴a=3.∴b2=a2-c2=3.当焦点在y轴上时,∵椭圆过点P(3,0),∴b=3.解析答案圆锥曲线中的许多问题,若能运用函数与方程的思想去分析,则往往能较快地找到解题的突破口.用函数思想解决圆锥曲线中的有关定值、最值问题,最值问题是高中数学中常见的问题,在圆锥曲线问题中也不例外,而函数思想是解决最值问题最有利的武器.我们通常可用建立目标函数的方法解有关圆锥曲线的最值问题.
方程思想是从分析问题的数量关系入手,通过联想与类比,将问题中的条件转化为方程或方程组,然后通过解方程或方程组使问题获解,方程思想是高中数学中最基本、最重要的思想方法之一,在高考中占有非常重要的地位.在求圆锥曲线方程、直线与圆锥曲线的位置关系的问题中经常利用方程或方程组来解决.3.函数与方程思想解析答案例3 已知椭圆ax2+by2=1(a>0,b>0且a≠b)与直线x+y-1=0相交于A,B两点,C是AB的中点,求椭圆的方程.解 方法一 设A(x1,y1),B(x2,y2),代入椭圆方程并作差,得
a(x1+x2)(x1-x2)+b(y1+y2)(y1-y2)=0. ①直线x+y-1=0的斜率k=-1.∴|x2-x1|=2.
联立ax2+by2=1与x+y-1=0可得(a+b)x2-2bx+b-1=0.解析答案解析答案得(a+b)x2-2bx+b-1=0.设A(x1,y1),B(x2,y2),解析答案解析答案得a=3.34.化归与转化思想将所研究的对象在一定条件下转化并归结为另一种研究对象的思想方法称之为化归与转化思想.一般将有待解决的问题进行转化,使之成为大家熟悉的或容易解决的问题模式.转化与化归思想在圆锥曲线中经常应用,如把直线与圆锥曲线的位置关系问题转化为方程组的解的个数问题,把求参数的取值范围问题转化为解不等式(组)问题,把陌生的问题转化为熟悉的问题,需要注意转化的等价性.例4 已知点A(4,-2),F为抛物线y2=8x的焦点,点M在抛物线上移动,当MA+MF取最小值时,点M的坐标为________.解析答案解析 过点M作准线l的垂线,垂足为E,由抛物线定义知MF=ME.
当点M在抛物线上移动时,MF+MA的值在变化,
显然M移到M′,AM′∥Ox时,
A,M,E共线,此时ME+MA最小,解析答案(1)求点Q(x,y)的轨迹C的方程;解 由题意得,解析答案(2)设曲线C与直线y=kx+m相交于不同的两点M、N,又点A(0,-1),当AM=AN时,求实数m的取值范围.得(3k2+1)x2+6mkx+3(m2-1)=0,
由于直线与椭圆有两个不同的交点,
∴Δ>0,即m2<3k2+1. ①(ⅰ)当k≠0时,设弦MN的中点为P(xP,yP),xM、xN分别为点M、N的横坐标,解析答案又AM=AN,∴AP⊥MN.将②代入①得2m>m2,解得0
3.虽然考纲中没有直接要求关于直线与圆锥曲线相结合的知识,但直线与圆锥曲线是密不可分的,如双曲线的渐近线、抛物线的准线,圆锥曲线的对称轴等都是直线.考试不但不回避直线与圆锥曲线,而且在试题中进行重点考查,考查方式既可以是填空题,也可以是解答题.课堂小结4.考纲对曲线与方程的要求是“了解方程的曲线与曲线的方程的对应关系”,考试对曲线与方程的考查主要体现在以利用圆锥曲线的定义、待定系数法、直接法和代入法等方法求圆锥曲线的方程.
5.对圆锥曲线的考查是综合性的,这种综合性体现在圆锥曲线、直线、圆、平面向量、不等式等知识的相互交汇,对圆锥曲线的综合考查主要是在解答题中进行,一般以椭圆或者抛物线为依托,全面考查圆锥曲线与方程的求法、直线与圆锥曲线的位置关系,考查函数、方程、不等式、平面向量等在解决问题中的综合运用.返回
