10.3.1 图形的旋转 同步练习
文档属性
| 名称 | 10.3.1 图形的旋转 同步练习 |  | |
| 格式 | zip | ||
| 文件大小 | 522.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-22 18:36:50 | ||
图片预览



文档简介
10.3.1 图形的旋转
核心笔记: 1.旋转的概念:在平面内,将一个图形绕一个定点沿某个方向转动一定的角度,像这样的运动称为旋转.这个定点称为旋转中心,转动的角称为旋转角.www.21-cn-jy.com
2.一个图形旋转后形成另一个图形.这两个图形中,能重合的点叫做对应点,能重合的线段叫做对应线段,能重合的角叫做对应角.
3.旋转三要素:①旋转中心;②旋转方向;③旋转角度.
基础训练
1.下列现象中是旋转的是( )
A.车轮在水平地面上滚动
B.火车车厢的直线运动
C.电梯的上下移动
D.汽车方向盘的转动
2.将图中的正方形图案绕中心旋转180°后,得到的图案是( )
3.用方块布料缝制一块挂毯,方块形成的花纹如图所示.应该选择给出的四块布料中的( )填在图中①的位置,才能使花纹保持原来的模式.21世纪教育网版权所有
4.如图,△ABC与△BDE都是等腰直角三角形,∠ACB和∠E都是直角,若△ABC经逆时针旋转后能与△DBE重合,则旋转中心是点 ,旋转的角度是 .?21cnjy.com
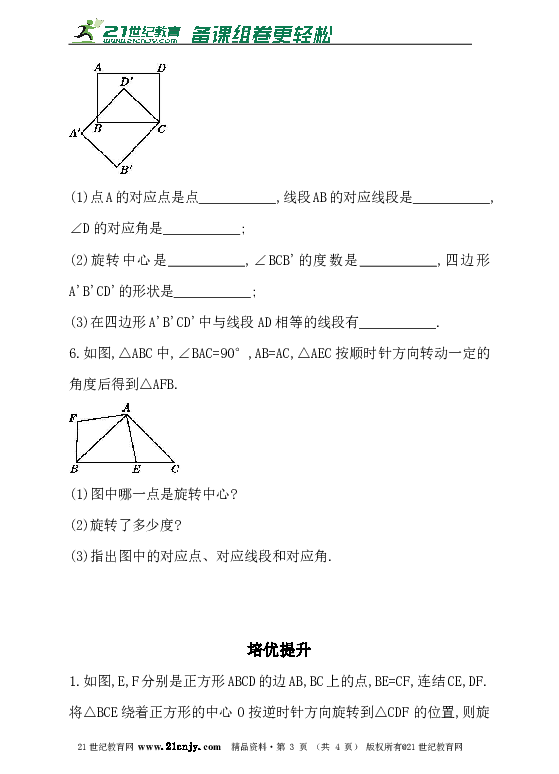
5.如图,长方形ABCD绕点C按逆时针方向旋转45°后得到图形A'B'CD'.请回答下列问题:
(1)点A的对应点是点___________,线段AB的对应线段是___________,∠D的对应角是___________;2·1·c·n·j·y
(2)旋转中心是___________,∠BCB'的度数是___________,四边形A'B'CD'的形状是___________;?【来源:21·世纪·教育·网】
(3)在四边形A'B'CD'中与线段AD相等的线段有___________.
6.如图,△ABC中,∠BAC=90°,AB=AC,△AEC按顺时针方向转动一定的角度后得到△AFB.21·世纪*教育网
(1)图中哪一点是旋转中心?
(2)旋转了多少度?
(3)指出图中的对应点、对应线段和对应角.
培优提升
1.如图,E,F分别是正方形ABCD的边AB,BC上的点,BE=CF,连结CE,DF.将△BCE绕着正方形的中心O按逆时针方向旋转到△CDF的位置,则旋转角是( )www-2-1-cnjy-com
A.45° B.60° C.90° D.120°
2.按图中第一、二行图形的变换规律,填入第三行“?”处的图形应是( )
3.如图,在直角三角形OAB中,∠AOB=30°,将△AOB绕点O逆时针旋转100°得到△A1OB1,则∠A1OB的度数为 .?2-1-c-n-j-y
4.如图,△ABC为等边三角形,D为△ABC内一点,△ABD经过旋转后到达△ACP的位置.
(1)旋转中心是______________;
(2)旋转的角度是______________度.?
5.如图,在方格纸中,△ABC的三个顶点和点P都在小方格的顶点上.以点C为旋转中心,将△ABC旋转,使点P落在旋转后的三角形内部,且旋转后的三角形的各顶点在小方格的顶点上.画出旋转后的三角形.
6.如图所示,正方形ABCD的边长为7,△ABE是由△ADF旋转得到的,已知AF=4.
(1)△ADF旋转得到△ABE的过程中,旋转中心为点 ,旋转角度为 .?
(2)求DE的长度.
7.如图,△ACD、△AEB都是等腰直角三角形,∠CAD=∠EAB=90°,∠BAC=30°,若△EAC逆时针旋转后能与△BAD重合.21*cnjy*com
(1)旋转中心是哪一点?
(2)旋转角为多少度?
(3)若BD=5 cm,求EC的长度.
8.钟表的分针匀速旋转一周需要60 min.
(1)经过18 min,分针和时针各旋转了多少度?
(2)从12时整开始计时,经过多少分,分针旋转的角度和时针旋转的角度第一次相差90°?
9.在正方形ABCD中,点E在BC上,点F在AB上,∠FDE=45°,△DEC按顺时针方向旋转一个角度后得到△DGA,如图所示.【来源:21cnj*y.co*m】
(1)哪一个点是旋转中心?旋转角是多少度?
(2)指出图中的对应线段和对应角.
(3)求∠GDF的度数.
参考答案
【基础训练】
1.【答案】D
解:在平面内,将一个图形绕一个定点沿着某个方向旋转一定的角度的图形变换叫做旋转.据此可得到答案.
2.【答案】C 3.【答案】D
4.【答案】B;45°
5.【答案】(1)A';A'B';∠D' (2)点C;45°;长方形
(3)A'D',B'C
分析:解题的关键是熟练掌握旋转的定义和性质.
6.解:(1)点A是旋转中心.
(2)∠BAC为旋转角,所以,旋转了90°.
(3)点A与点A,点C与点B,点E与点F是对应点,
线段AE与AF,线段AC与AB,线段EC与FB是对应线段,
∠CAE与∠BAF,∠ACE与∠ABF,∠AEC与∠AFB是对应角.
【培优提升】
1.【答案】C
解:如图,
连结AC,BD,AC与BD的交点即为旋转中心O.
根据旋转的性质知,点C与点D为对应点,则∠DOC就是旋转角.
∵四边形ABCD是正方形,
∴∠DOC=90°.
2.【答案】B
解:根据第一、二行图形的变换规律,将第三行第二个图形顺时针旋转90°,即可确定为B.
3.【答案】70°
4.【答案】(1)点A (2)60
5.解:如图所示.
6.解:(1)A;90°
(2)∵正方形ABCD的边长为7,△ABE是由△ADF旋转得到的,AF=4,
∴AE=AF=4,∴DE=AD-AE=7-4=3.
7.解:(1)∵△EAC逆时针旋转后能与△BAD重合,
A点为两三角形的公共顶点,∴旋转中心是A点.
(2)∵△EAC逆时针旋转后能与△BAD重合,
∴AE与AB为对应线段,
∵∠BAE=90°,
∴旋转角为90°.
(3)由题意知EC和BD是对应线段,根据旋转的性质可得EC=BD=5 cm.
8.解:(1)分针匀速旋转一周需60 min,因此经过18 min,
分针旋转的角度为×18=108°.时针旋转的角度为×18=9°.
(2)设经过x分,分针旋转的角度和时针旋转的角度第一次相差90°,则6x-0.5x=90,解得x==16.21教育网
所以经过16分,分针旋转的角度和时针旋转的角度第一次相差90°.
分析:解决此题需要掌握以下数据:分针匀速旋转一周需60 min,时针匀速旋转一周需12×60=720(min),所以分针每分钟旋转=6°,时针每分钟旋转=0.5°.21·cn·jy·com
9.解:(1)D点是旋转中心,旋转角是90°.
(2)对应线段是DE和DG,DC和DA,CE和AG.
对应角是∠CDE和∠ADG,∠C和∠DAG,∠DEC和∠G.
(3)∵∠FDE=45°,∠ADC=90°,
∴∠ADF+∠EDC=90°-45°=45°,
∵∠GDF=∠GDA+∠ADF,∠GDA=∠EDC,
∴∠GDF=∠EDC+∠ADF=45°.
分析:本题考查了旋转的性质,旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变.
核心笔记: 1.旋转的概念:在平面内,将一个图形绕一个定点沿某个方向转动一定的角度,像这样的运动称为旋转.这个定点称为旋转中心,转动的角称为旋转角.www.21-cn-jy.com
2.一个图形旋转后形成另一个图形.这两个图形中,能重合的点叫做对应点,能重合的线段叫做对应线段,能重合的角叫做对应角.
3.旋转三要素:①旋转中心;②旋转方向;③旋转角度.
基础训练
1.下列现象中是旋转的是( )
A.车轮在水平地面上滚动
B.火车车厢的直线运动
C.电梯的上下移动
D.汽车方向盘的转动
2.将图中的正方形图案绕中心旋转180°后,得到的图案是( )
3.用方块布料缝制一块挂毯,方块形成的花纹如图所示.应该选择给出的四块布料中的( )填在图中①的位置,才能使花纹保持原来的模式.21世纪教育网版权所有
4.如图,△ABC与△BDE都是等腰直角三角形,∠ACB和∠E都是直角,若△ABC经逆时针旋转后能与△DBE重合,则旋转中心是点 ,旋转的角度是 .?21cnjy.com
5.如图,长方形ABCD绕点C按逆时针方向旋转45°后得到图形A'B'CD'.请回答下列问题:
(1)点A的对应点是点___________,线段AB的对应线段是___________,∠D的对应角是___________;2·1·c·n·j·y
(2)旋转中心是___________,∠BCB'的度数是___________,四边形A'B'CD'的形状是___________;?【来源:21·世纪·教育·网】
(3)在四边形A'B'CD'中与线段AD相等的线段有___________.
6.如图,△ABC中,∠BAC=90°,AB=AC,△AEC按顺时针方向转动一定的角度后得到△AFB.21·世纪*教育网
(1)图中哪一点是旋转中心?
(2)旋转了多少度?
(3)指出图中的对应点、对应线段和对应角.
培优提升
1.如图,E,F分别是正方形ABCD的边AB,BC上的点,BE=CF,连结CE,DF.将△BCE绕着正方形的中心O按逆时针方向旋转到△CDF的位置,则旋转角是( )www-2-1-cnjy-com
A.45° B.60° C.90° D.120°
2.按图中第一、二行图形的变换规律,填入第三行“?”处的图形应是( )
3.如图,在直角三角形OAB中,∠AOB=30°,将△AOB绕点O逆时针旋转100°得到△A1OB1,则∠A1OB的度数为 .?2-1-c-n-j-y
4.如图,△ABC为等边三角形,D为△ABC内一点,△ABD经过旋转后到达△ACP的位置.
(1)旋转中心是______________;
(2)旋转的角度是______________度.?
5.如图,在方格纸中,△ABC的三个顶点和点P都在小方格的顶点上.以点C为旋转中心,将△ABC旋转,使点P落在旋转后的三角形内部,且旋转后的三角形的各顶点在小方格的顶点上.画出旋转后的三角形.
6.如图所示,正方形ABCD的边长为7,△ABE是由△ADF旋转得到的,已知AF=4.
(1)△ADF旋转得到△ABE的过程中,旋转中心为点 ,旋转角度为 .?
(2)求DE的长度.
7.如图,△ACD、△AEB都是等腰直角三角形,∠CAD=∠EAB=90°,∠BAC=30°,若△EAC逆时针旋转后能与△BAD重合.21*cnjy*com
(1)旋转中心是哪一点?
(2)旋转角为多少度?
(3)若BD=5 cm,求EC的长度.
8.钟表的分针匀速旋转一周需要60 min.
(1)经过18 min,分针和时针各旋转了多少度?
(2)从12时整开始计时,经过多少分,分针旋转的角度和时针旋转的角度第一次相差90°?
9.在正方形ABCD中,点E在BC上,点F在AB上,∠FDE=45°,△DEC按顺时针方向旋转一个角度后得到△DGA,如图所示.【来源:21cnj*y.co*m】
(1)哪一个点是旋转中心?旋转角是多少度?
(2)指出图中的对应线段和对应角.
(3)求∠GDF的度数.
参考答案
【基础训练】
1.【答案】D
解:在平面内,将一个图形绕一个定点沿着某个方向旋转一定的角度的图形变换叫做旋转.据此可得到答案.
2.【答案】C 3.【答案】D
4.【答案】B;45°
5.【答案】(1)A';A'B';∠D' (2)点C;45°;长方形
(3)A'D',B'C
分析:解题的关键是熟练掌握旋转的定义和性质.
6.解:(1)点A是旋转中心.
(2)∠BAC为旋转角,所以,旋转了90°.
(3)点A与点A,点C与点B,点E与点F是对应点,
线段AE与AF,线段AC与AB,线段EC与FB是对应线段,
∠CAE与∠BAF,∠ACE与∠ABF,∠AEC与∠AFB是对应角.
【培优提升】
1.【答案】C
解:如图,
连结AC,BD,AC与BD的交点即为旋转中心O.
根据旋转的性质知,点C与点D为对应点,则∠DOC就是旋转角.
∵四边形ABCD是正方形,
∴∠DOC=90°.
2.【答案】B
解:根据第一、二行图形的变换规律,将第三行第二个图形顺时针旋转90°,即可确定为B.
3.【答案】70°
4.【答案】(1)点A (2)60
5.解:如图所示.
6.解:(1)A;90°
(2)∵正方形ABCD的边长为7,△ABE是由△ADF旋转得到的,AF=4,
∴AE=AF=4,∴DE=AD-AE=7-4=3.
7.解:(1)∵△EAC逆时针旋转后能与△BAD重合,
A点为两三角形的公共顶点,∴旋转中心是A点.
(2)∵△EAC逆时针旋转后能与△BAD重合,
∴AE与AB为对应线段,
∵∠BAE=90°,
∴旋转角为90°.
(3)由题意知EC和BD是对应线段,根据旋转的性质可得EC=BD=5 cm.
8.解:(1)分针匀速旋转一周需60 min,因此经过18 min,
分针旋转的角度为×18=108°.时针旋转的角度为×18=9°.
(2)设经过x分,分针旋转的角度和时针旋转的角度第一次相差90°,则6x-0.5x=90,解得x==16.21教育网
所以经过16分,分针旋转的角度和时针旋转的角度第一次相差90°.
分析:解决此题需要掌握以下数据:分针匀速旋转一周需60 min,时针匀速旋转一周需12×60=720(min),所以分针每分钟旋转=6°,时针每分钟旋转=0.5°.21·cn·jy·com
9.解:(1)D点是旋转中心,旋转角是90°.
(2)对应线段是DE和DG,DC和DA,CE和AG.
对应角是∠CDE和∠ADG,∠C和∠DAG,∠DEC和∠G.
(3)∵∠FDE=45°,∠ADC=90°,
∴∠ADF+∠EDC=90°-45°=45°,
∵∠GDF=∠GDA+∠ADF,∠GDA=∠EDC,
∴∠GDF=∠EDC+∠ADF=45°.
分析:本题考查了旋转的性质,旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变.
