10.3.2 旋转的特征 同步练习
文档属性
| 名称 | 10.3.2 旋转的特征 同步练习 |

|
|
| 格式 | zip | ||
| 文件大小 | 470.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-22 18:39:50 | ||
图片预览


文档简介
10.3.2 旋转的特征
核心笔记: 1.旋转的特征:图形中每一点都绕着旋转中心按同一旋转方向旋转了同样大小的角度,对应点到旋转中心的距离相等,对应线段相等,对应角相等,图形的形状与大小不变.21cnjy.com
2.旋转作图的步骤:
(1)确定旋转中心及旋转方向、旋转角.
(2)找出表示图形的关键点.
(3)将图形的关键点与旋转中心连结起来,然后按旋转方向分别将它们旋转一个角度,得到各关键点的对应点.2·1·c·n·j·y
(4)按原图形的形状连结这些对应点,得到的图形就是旋转后的图形.
因此确定一个图形旋转后的图形所需条件是:①图形原来的位置;②旋转中心、方向;③旋转角的大小.
基础训练
1.下列说法中,错误的是( )
A.图形经过旋转后,对应线段、对应角都相等,并且对应线段平行
B.图形经过旋转后,对应点到旋转中心的距离相等
C.图形经过旋转后,图形的形状与大小都没有发生变化
D.旋转时,图形中的每一点都绕着旋转中心按同一旋转方向旋转
2.如图,将直角三角形ABC(其中∠B=35°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点C,A,B1在同一条直线上,那么旋转角等于( )【来源:21·世纪·教育·网】
A.55° B.70° C.125° D.145°
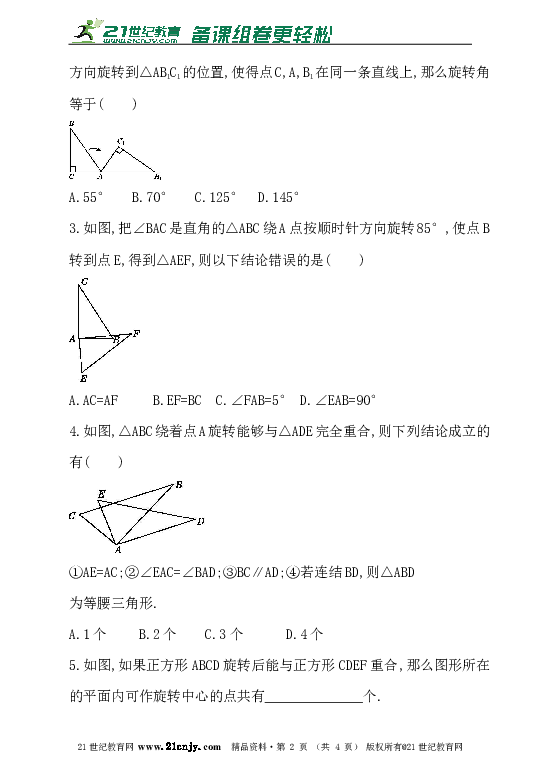
3.如图,把∠BAC是直角的△ABC绕A点按顺时针方向旋转85°,使点B转到点E,得到△AEF,则以下结论错误的是( )21·cn·jy·com
A.AC=AF B.EF=BC C.∠FAB=5° D.∠EAB=90°
4.如图,△ABC绕着点A旋转能够与△ADE完全重合,则下列结论成立的有( )
①AE=AC;②∠EAC=∠BAD;③BC∥AD;④若连结BD,则△ABD
为等腰三角形.
A.1个 B.2个 C.3个 D.4个
5.如图,如果正方形ABCD旋转后能与正方形CDEF重合,那么图形所在的平面内可作旋转中心的点共有______________个.21·世纪*教育网
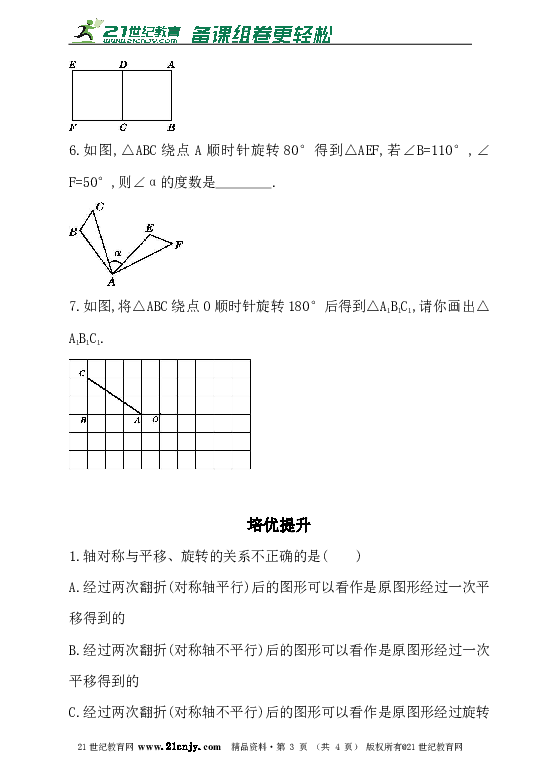
6.如图,△ABC绕点A顺时针旋转80°得到△AEF,若∠B=110°,∠F=50°,则∠α的度数是 .www-2-1-cnjy-com
7.如图,将△ABC绕点O顺时针旋转180°后得到△A1B1C1,请你画出△A1B1C1.
培优提升
1.轴对称与平移、旋转的关系不正确的是( )
A.经过两次翻折(对称轴平行)后的图形可以看作是原图形经过一次平移得到的
B.经过两次翻折(对称轴不平行)后的图形可以看作是原图形经过一次平移得到的
C.经过两次翻折(对称轴不平行)后的图形可以看作是原图形经过旋转得到的
D.经过几次翻折(对称轴有偶数条且平行)后的图形可以看作是经过一次平移得到的
2.如图所示,△ABC绕着点O按顺时针方向旋转90°之后到了△CDE的位置,下列说法不正确的是( )21教育网
A.线段AB与线段CD互相垂直 B.点C与点C是两个三角形的对应点
C.线段AC与线段CE互相垂直 D.线段BC与线段DE互相垂直
3.如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB'C'的位置,使得CC'∥AB,则∠BAB'等于( )
A.30° B.35° C.40° D.50°
4.如图,△AOB中,∠B=30°.将△AOB绕点O顺时针旋转52°得到△A'OB',边A'B'与边OB交于点C(A'不在OB上),则∠A'CO的度数为 .www.21-cn-jy.com
5.如图,在4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1,则旋转中心是点 .?21*cnjy*com
6.用等腰直角三角尺画∠AOB=45°,并将三角尺沿OB方向平移到如图所示的虚线处,然后将其绕点M按逆时针方向旋转22°,则三角尺的斜边与边OA的夹角α为____________.【来源:21cnj*y.co*m】
7.如图,在等腰直角三角形ABC中,AD为斜边上的高,点E,F分别在AB,AC上,△AED经过旋转到了△CFD的位置. 【出处:21教育名师】
(1)△BED和△AFD之间可以看成是经过怎样的变换得到的?
(2)AD与EF相交于点G,试判断∠AED与∠AGF的大小关系,并说明理由.
8.如图①,将一副直角三角尺放在同一条直线AB上,其中∠MNO=30°,∠OCD=45°.
(1)将图①中的三角尺OCD沿AB的方向平移,使得点O与点N重合,CD与MN相交于点E,如图②所示.求∠CEN的度数.2-1-c-n-j-y
(2)将图①中的三角尺OCD绕点O按顺时针方向旋转,使一边OD在∠MON的内部,如图③,且OD恰好平分∠MON,CD与MN相交于点E,求∠CEN的度数.【版权所有:21教育】
(3)将图①中的三角尺OCD绕点O按每秒15°的速度按顺时针方向旋转一周,在旋转的过程中,在第_________秒时,边CD恰好与边MN平行;在第_________秒时,边CD恰好与边MN垂直.(直接写出结果)?
参考答案
【基础训练】
1.【答案】A
2.【答案】C
解:∵∠B=35°,∠C=90°,∴∠BAC=90°-∠B=90°-35°=55°.∵点C,A,B1在同一条直线上,21教育名师原创作品
∴∠BAB1=180°-∠BAC=180°-55°=125°,∴旋转角等于125°.故选C.
3.【答案】D
解:根据旋转的性质可以得到:AC=AF,EF=BC,故A、B是正确的;∠FAB=∠CAB-∠CAF=21*cnjy*com
90°-85°=5°,故选项C正确;∠EAB是旋转角,是85°,故D错误.
4.【答案】C
5.【答案】3
解:如图所示,以点D为旋转中心,顺时针旋转90°,正方形ABCD能与正方形CDEF重合;以点C为旋转中心,逆时针旋转90°,正方形ABCD能与正方形CDEF重合;以CD的中点为旋转中心,顺(或逆)时针旋转180°,正方形ABCD能与正方形CDEF重合.所以图形所在的平面内可作旋转中心的点共有3个.
6.【答案】60°
解:∵△ABC绕点A顺时针旋转80°得到△AEF,∴∠C=∠F=50°,∠BAE=80°.∵∠B=110°,∴∠BAC=180°-∠B-∠C=180°-110°-50°=20°,∴∠α=80°-20°=60°.
7.解:如图所示.
【培优提升】
1.【答案】B
2.【答案】B
解:△ABC在旋转过程中,点A旋转到点C,点B旋转到点D,点C旋转到点E,因为△ABC旋转了90°,所以AC⊥CE,AB⊥CD,BC⊥DE.
3.【答案】A
解:∵△ABC绕点A旋转到△AB'C'的位置,
∴AC=AC',∠BAC=∠B'AC',∴∠AC'C=∠ACC'.∵CC'∥AB,∠CAB=75°,∴∠ACC'=∠CAB=75°,∴∠CAC'=180°-2∠ACC'=180°-2×75°=30°.∵∠BAB'=∠BAC-∠B'AC,∠CAC'=∠B'AC'-∠B'AC,∴∠BAB'=∠CAC'=30°.故选A.21世纪教育网版权所有
4.【答案】82°
解:∵△A'OB'是由△AOB绕点O顺时针旋转得到的,∠B=30°,∴∠B'=∠B=30°.∵△AOB绕点O顺时针旋转52°,∴∠BOB'=52°.∵∠A'CO是△B'OC的外角,∴∠A'CO=∠B'+∠BOB'=30°+52°=82°.
5.【答案】B
6.【答案】22°
7.解:(1)∵△AED经过旋转到了△CFD的位置,
∴DE=DF,AD=CD,AE=CF,∠EDF=∠ADC.
∵在等腰直角三角形ABC中,AD为斜边上的高,
∴AD=CD=BD,∠ADC=∠ADB=90°,AB=AC,
∴∠EDF=90°,BE=AF,
∴△AFD可以看成是由△BED绕点D按顺时针方向旋转90°得到的.
(2)∠AED=∠AGF.
理由:∵DF=DE,∠FDE=90°,
∴∠DFE=∠DEF=45°.
∵AB=AC,AD⊥BC,
∴∠BAD=∠CAD=45°.
∵∠AGF=∠DAE+∠AEG=45°+∠AEG,
∠AED=∠DEF+∠AEF=45°+∠AEG,
∴∠AED=∠AGF.
8.解:(1)在△CEN中,
∠CEN=180°-∠DCN-∠MNO
=180°-45°-30°
=105°.
(2)∵OD平分∠MON,
∴∠DON=∠MON=×90°=45°,
∴∠DON=∠D,
∴CD∥AB,
∴∠CEN=180°-∠MNO=180°-30°=150°.
(3)5或17;11或23
分析:本题考查了旋转的性质,三角形的内角和定理,三角形的一个外角等于与它不相邻的两个内角的和的性质,直角三角形的两个锐角互余的性质,熟记各性质并熟悉三角尺各角的度数是解题的关键.
核心笔记: 1.旋转的特征:图形中每一点都绕着旋转中心按同一旋转方向旋转了同样大小的角度,对应点到旋转中心的距离相等,对应线段相等,对应角相等,图形的形状与大小不变.21cnjy.com
2.旋转作图的步骤:
(1)确定旋转中心及旋转方向、旋转角.
(2)找出表示图形的关键点.
(3)将图形的关键点与旋转中心连结起来,然后按旋转方向分别将它们旋转一个角度,得到各关键点的对应点.2·1·c·n·j·y
(4)按原图形的形状连结这些对应点,得到的图形就是旋转后的图形.
因此确定一个图形旋转后的图形所需条件是:①图形原来的位置;②旋转中心、方向;③旋转角的大小.
基础训练
1.下列说法中,错误的是( )
A.图形经过旋转后,对应线段、对应角都相等,并且对应线段平行
B.图形经过旋转后,对应点到旋转中心的距离相等
C.图形经过旋转后,图形的形状与大小都没有发生变化
D.旋转时,图形中的每一点都绕着旋转中心按同一旋转方向旋转
2.如图,将直角三角形ABC(其中∠B=35°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点C,A,B1在同一条直线上,那么旋转角等于( )【来源:21·世纪·教育·网】
A.55° B.70° C.125° D.145°
3.如图,把∠BAC是直角的△ABC绕A点按顺时针方向旋转85°,使点B转到点E,得到△AEF,则以下结论错误的是( )21·cn·jy·com
A.AC=AF B.EF=BC C.∠FAB=5° D.∠EAB=90°
4.如图,△ABC绕着点A旋转能够与△ADE完全重合,则下列结论成立的有( )
①AE=AC;②∠EAC=∠BAD;③BC∥AD;④若连结BD,则△ABD
为等腰三角形.
A.1个 B.2个 C.3个 D.4个
5.如图,如果正方形ABCD旋转后能与正方形CDEF重合,那么图形所在的平面内可作旋转中心的点共有______________个.21·世纪*教育网
6.如图,△ABC绕点A顺时针旋转80°得到△AEF,若∠B=110°,∠F=50°,则∠α的度数是 .www-2-1-cnjy-com
7.如图,将△ABC绕点O顺时针旋转180°后得到△A1B1C1,请你画出△A1B1C1.
培优提升
1.轴对称与平移、旋转的关系不正确的是( )
A.经过两次翻折(对称轴平行)后的图形可以看作是原图形经过一次平移得到的
B.经过两次翻折(对称轴不平行)后的图形可以看作是原图形经过一次平移得到的
C.经过两次翻折(对称轴不平行)后的图形可以看作是原图形经过旋转得到的
D.经过几次翻折(对称轴有偶数条且平行)后的图形可以看作是经过一次平移得到的
2.如图所示,△ABC绕着点O按顺时针方向旋转90°之后到了△CDE的位置,下列说法不正确的是( )21教育网
A.线段AB与线段CD互相垂直 B.点C与点C是两个三角形的对应点
C.线段AC与线段CE互相垂直 D.线段BC与线段DE互相垂直
3.如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB'C'的位置,使得CC'∥AB,则∠BAB'等于( )
A.30° B.35° C.40° D.50°
4.如图,△AOB中,∠B=30°.将△AOB绕点O顺时针旋转52°得到△A'OB',边A'B'与边OB交于点C(A'不在OB上),则∠A'CO的度数为 .www.21-cn-jy.com
5.如图,在4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1,则旋转中心是点 .?21*cnjy*com
6.用等腰直角三角尺画∠AOB=45°,并将三角尺沿OB方向平移到如图所示的虚线处,然后将其绕点M按逆时针方向旋转22°,则三角尺的斜边与边OA的夹角α为____________.【来源:21cnj*y.co*m】
7.如图,在等腰直角三角形ABC中,AD为斜边上的高,点E,F分别在AB,AC上,△AED经过旋转到了△CFD的位置. 【出处:21教育名师】
(1)△BED和△AFD之间可以看成是经过怎样的变换得到的?
(2)AD与EF相交于点G,试判断∠AED与∠AGF的大小关系,并说明理由.
8.如图①,将一副直角三角尺放在同一条直线AB上,其中∠MNO=30°,∠OCD=45°.
(1)将图①中的三角尺OCD沿AB的方向平移,使得点O与点N重合,CD与MN相交于点E,如图②所示.求∠CEN的度数.2-1-c-n-j-y
(2)将图①中的三角尺OCD绕点O按顺时针方向旋转,使一边OD在∠MON的内部,如图③,且OD恰好平分∠MON,CD与MN相交于点E,求∠CEN的度数.【版权所有:21教育】
(3)将图①中的三角尺OCD绕点O按每秒15°的速度按顺时针方向旋转一周,在旋转的过程中,在第_________秒时,边CD恰好与边MN平行;在第_________秒时,边CD恰好与边MN垂直.(直接写出结果)?
参考答案
【基础训练】
1.【答案】A
2.【答案】C
解:∵∠B=35°,∠C=90°,∴∠BAC=90°-∠B=90°-35°=55°.∵点C,A,B1在同一条直线上,21教育名师原创作品
∴∠BAB1=180°-∠BAC=180°-55°=125°,∴旋转角等于125°.故选C.
3.【答案】D
解:根据旋转的性质可以得到:AC=AF,EF=BC,故A、B是正确的;∠FAB=∠CAB-∠CAF=21*cnjy*com
90°-85°=5°,故选项C正确;∠EAB是旋转角,是85°,故D错误.
4.【答案】C
5.【答案】3
解:如图所示,以点D为旋转中心,顺时针旋转90°,正方形ABCD能与正方形CDEF重合;以点C为旋转中心,逆时针旋转90°,正方形ABCD能与正方形CDEF重合;以CD的中点为旋转中心,顺(或逆)时针旋转180°,正方形ABCD能与正方形CDEF重合.所以图形所在的平面内可作旋转中心的点共有3个.
6.【答案】60°
解:∵△ABC绕点A顺时针旋转80°得到△AEF,∴∠C=∠F=50°,∠BAE=80°.∵∠B=110°,∴∠BAC=180°-∠B-∠C=180°-110°-50°=20°,∴∠α=80°-20°=60°.
7.解:如图所示.
【培优提升】
1.【答案】B
2.【答案】B
解:△ABC在旋转过程中,点A旋转到点C,点B旋转到点D,点C旋转到点E,因为△ABC旋转了90°,所以AC⊥CE,AB⊥CD,BC⊥DE.
3.【答案】A
解:∵△ABC绕点A旋转到△AB'C'的位置,
∴AC=AC',∠BAC=∠B'AC',∴∠AC'C=∠ACC'.∵CC'∥AB,∠CAB=75°,∴∠ACC'=∠CAB=75°,∴∠CAC'=180°-2∠ACC'=180°-2×75°=30°.∵∠BAB'=∠BAC-∠B'AC,∠CAC'=∠B'AC'-∠B'AC,∴∠BAB'=∠CAC'=30°.故选A.21世纪教育网版权所有
4.【答案】82°
解:∵△A'OB'是由△AOB绕点O顺时针旋转得到的,∠B=30°,∴∠B'=∠B=30°.∵△AOB绕点O顺时针旋转52°,∴∠BOB'=52°.∵∠A'CO是△B'OC的外角,∴∠A'CO=∠B'+∠BOB'=30°+52°=82°.
5.【答案】B
6.【答案】22°
7.解:(1)∵△AED经过旋转到了△CFD的位置,
∴DE=DF,AD=CD,AE=CF,∠EDF=∠ADC.
∵在等腰直角三角形ABC中,AD为斜边上的高,
∴AD=CD=BD,∠ADC=∠ADB=90°,AB=AC,
∴∠EDF=90°,BE=AF,
∴△AFD可以看成是由△BED绕点D按顺时针方向旋转90°得到的.
(2)∠AED=∠AGF.
理由:∵DF=DE,∠FDE=90°,
∴∠DFE=∠DEF=45°.
∵AB=AC,AD⊥BC,
∴∠BAD=∠CAD=45°.
∵∠AGF=∠DAE+∠AEG=45°+∠AEG,
∠AED=∠DEF+∠AEF=45°+∠AEG,
∴∠AED=∠AGF.
8.解:(1)在△CEN中,
∠CEN=180°-∠DCN-∠MNO
=180°-45°-30°
=105°.
(2)∵OD平分∠MON,
∴∠DON=∠MON=×90°=45°,
∴∠DON=∠D,
∴CD∥AB,
∴∠CEN=180°-∠MNO=180°-30°=150°.
(3)5或17;11或23
分析:本题考查了旋转的性质,三角形的内角和定理,三角形的一个外角等于与它不相邻的两个内角的和的性质,直角三角形的两个锐角互余的性质,熟记各性质并熟悉三角尺各角的度数是解题的关键.
