10.5 图形的全等 同步练习
图片预览



文档简介
10.5 图形的全等
核心笔记: 1.全等图形:能够完全重合的两个图形叫做全等图形.
2.全等多边形的有关概念:能够完全重合的两个多边形叫做全等多边形;两个全等的多边形,经过变换而重合,相互重合的顶点叫做对应顶点,相互重合的边叫做对应边,相互重合的角叫做对应角.
3.全等多边形的性质:全等多边形的对应边相等,对应角相等.
4.全等多边形的判定方法:边、角分别对应相等的两个多边形全等.
5.全等三角形:因为三角形是特殊的多边形,所以全等多边形的性质和判定方法在全等三角形中仍然适用.
(1)全等三角形的对应边、对应角分别相等.
(2)如果两个三角形的边、角分别对应相等,那么这两个三角形全等.
基础训练
1.下列说法中:
①能够完全重合的两个三角形是全等三角形;
②一个图形经过平移、轴对称、旋转这样的变换后,位置变化了,但形状、大小没有改变,即平移、轴对称、旋转这样的变换前后的两个图形是全等图形;【来源:21·世纪·教育·网】
③面积相等的两个三角形是全等三角形;
④全等三角形的周长相等;
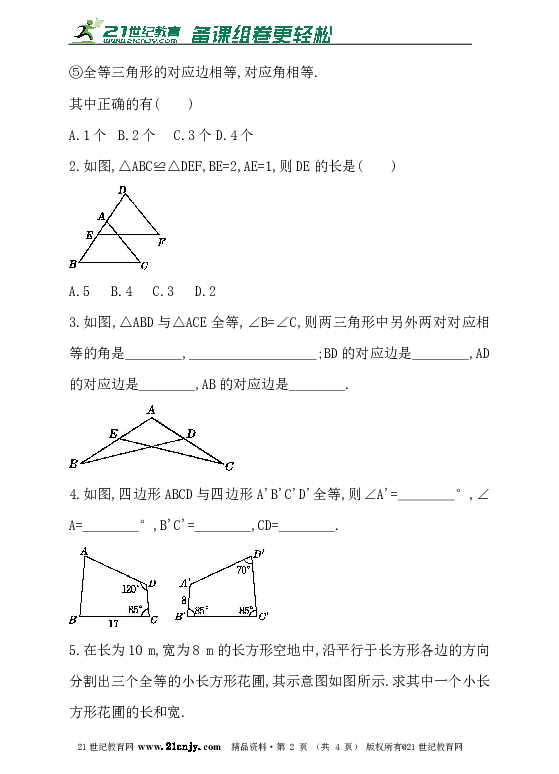
⑤全等三角形的对应边相等,对应角相等.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
2.如图,△ABC≌△DEF,BE=2,AE=1,则DE的长是( )
A.5 B.4 C.3 D.2
3.如图,△ABD与△ACE全等,∠B=∠C,则两三角形中另外两对对应相等的角是 , ;BD的对应边是 ,AD的对应边是 ,AB的对应边是 .21教育网
4.如图,四边形ABCD与四边形A'B'C'D'全等,则∠A'= °,∠A= °,B'C'= ,CD= .?www-2-1-cnjy-com
5.在长为10 m,宽为8 m的长方形空地中,沿平行于长方形各边的方向分割出三个全等的小长方形花圃,其示意图如图所示.求其中一个小长方形花圃的长和宽.【出处:21教育名师】
6.如图,△ABC≌△ADE,∠BAD=35°,∠D=55°,AD与BC交于点D,探究线段AD与BC的位置关系,并说明理由.21·世纪*教育网
培优提升
1.如图,四个图形中是全等图形的是( )
A.①和③ B.②和③ C.②和④ D.③和④
2.如图,△ABD≌△EBC,AB=5,BC=12,则DE的长为( )
A.5 B.6 C.7 D.8
3.如图,在△ABC中,D,E分别是边AC,BC上的点,若△ADB≌△EDB≌△EDC,则∠C的度数为( )2·1·c·n·j·y
A.15° B.20° C.25° D.30°
4.如图是由全等的图形组成的,其中AB=3 cm,CD=2AB,则AF=____________.
5.已知△DEF≌△ABC,AB=AC,且△ABC的周长为22 cm,BC=4 cm,则△DEF中最长的一条边的长为 .2-1-c-n-j-y
6.如图,△ABC≌△DEF,请根据图中提供的信息,写出x= .?
7.如图,△ABC≌△ADE,B点的对应点是D点,若∠BAD=100°,∠CAE=40°,则∠BAC的度数是 .21·cn·jy·com
8.如图,已知△ABF≌△DCE,E与F是对应点.
(1)△DCE可以看成是由△ABF通过怎样的运动得到的?
(2)试问AF,DE的位置关系如何?请说明你的理由.
9.如图,已知△ABC中,AB=AC=10厘米,BC=8厘米,点D为AB的中点,点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上以a厘米/秒的速度由C点向A点运动,设运动的时间为t秒.
(1)求CP的长;
(2)若以C,P,Q为顶点的三角形和以B,D,P为顶点的三角形全等,且∠B和∠C是对应角,求a的值.21世纪教育网版权所有
参考答案
【基础训练】
1.【答案】D
2.【答案】C
解:∵△ABC≌△DEF,∴DE=AB,∵BE=2,AE=1,∴DE=AB=BE+AE=2+1=3.故选C.【版权所有:21教育】
3.【答案】∠A=∠A;∠ADB=∠AEC;CE;AE;AC
4.【答案】120;70;17;8
解:根据全等图形能够完全重合且对应边、对应角分别相等可得出各角的度数.由题意得:∠A'=∠D=120°,∠A=∠D'=70°,B'C'=BC=17,CD=A'B'=8.21教育名师原创作品
5.解:∵三个小长方形全等,
∴它们的长均相等,宽也均相等.
设其中一个小长方形花圃的长为x m,宽为y m,由题图得解得则其中一个小长方形花圃的长和宽分别为4 m和2 m.
6.解:AD⊥BC.
理由如下:∵△ABC≌△ADE,∠D=55°,
∴∠B=∠D=55°,在△AOB中,∠AOB=180°-∠BAD-∠B=180°-35°-55°=90°,∴AD⊥BC.【来源:21cnj*y.co*m】
【培优提升】
1.【答案】C
解:能够完全重合的两个图形叫做全等图形,由此判断即可.
2.【答案】C
解:∵△ABD≌△EBC,AB=5,BC=12,∴BD=BC=12,BE=AB=5,∴DE=BD-BE=12-5=7.故选C.21*cnjy*com
3.【答案】D
解:∵△ADB≌△EDB≌△EDC,∴∠A=∠BED=∠CED,∠ABD=∠EBD=∠C.∵∠BED+∠CED=180°,∴∠A=∠BED=∠CED=90°.在△ABC中,∠C+2∠C+90°=180°,∴∠C=30°.故选D.21cnjy.com
4.【答案】27 cm
解:由全等图形的性质可知:AF=3AB+3CD=3AB+6AB=9AB=27 cm.
5.【答案】9 cm
解:∵△ABC的周长为22 cm,BC=4 cm,
∴AB=AC=×(22-4)=9(cm),∵△DEF≌△ABC,∴△DEF中最长的一条边的长为9 cm.21*cnjy*com
6.【答案】20
解:根据题意得EF=BC=20,即x=20.
7.【答案】70°
解:∵△ABC≌△ADE,
∴∠BAC=∠DAE,
∴∠BAC-∠CAE=∠DAE-∠CAE,
即∠BAE=∠DAC,
∵∠BAD=100°,∠CAE=40°,
∴∠BAE=(∠BAD-∠CAE)=×(100°-40°)=30°,
∴∠BAC=∠BAE+∠CAE=30°+40°=70°.
8.解:(1)△DCE可以看成是由△ABF沿BC方向平移,使F和E重合,然后再绕着E点顺(或逆)时针旋转180°得到的.(答案不唯一)
(2)AF∥DE.
理由:∵△ABF≌△DCE,
∴∠AFB=∠DEC,
∵∠AFB+∠AFE=180°,∠DEF+∠DEC=180°,
∴∠AFE=∠DEF,
∴AF∥DE.
9.解:(1)∵BP=3t厘米,BC=8厘米,
∴CP=(8-3t)厘米;
(2)①当BD=CP时,∵AB=10厘米,D为AB的中点,∴BD=5厘米,
∴5=8-3t,解得t=1,∵△BDP≌△CPQ,∴BP=CQ,即3×1=a×1,解得a=3;
②当BP=CP时,3t=8-3t,解得t=,∵△BDP≌△CQP,∴BD=CQ,即5=a×,解得a=,综上所述,a的值为3或.www.21-cn-jy.com
分析:本题考查了全等三角形的性质,(2)因为对应边不明确,所以要分情况讨论求解.
核心笔记: 1.全等图形:能够完全重合的两个图形叫做全等图形.
2.全等多边形的有关概念:能够完全重合的两个多边形叫做全等多边形;两个全等的多边形,经过变换而重合,相互重合的顶点叫做对应顶点,相互重合的边叫做对应边,相互重合的角叫做对应角.
3.全等多边形的性质:全等多边形的对应边相等,对应角相等.
4.全等多边形的判定方法:边、角分别对应相等的两个多边形全等.
5.全等三角形:因为三角形是特殊的多边形,所以全等多边形的性质和判定方法在全等三角形中仍然适用.
(1)全等三角形的对应边、对应角分别相等.
(2)如果两个三角形的边、角分别对应相等,那么这两个三角形全等.
基础训练
1.下列说法中:
①能够完全重合的两个三角形是全等三角形;
②一个图形经过平移、轴对称、旋转这样的变换后,位置变化了,但形状、大小没有改变,即平移、轴对称、旋转这样的变换前后的两个图形是全等图形;【来源:21·世纪·教育·网】
③面积相等的两个三角形是全等三角形;
④全等三角形的周长相等;
⑤全等三角形的对应边相等,对应角相等.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
2.如图,△ABC≌△DEF,BE=2,AE=1,则DE的长是( )
A.5 B.4 C.3 D.2
3.如图,△ABD与△ACE全等,∠B=∠C,则两三角形中另外两对对应相等的角是 , ;BD的对应边是 ,AD的对应边是 ,AB的对应边是 .21教育网
4.如图,四边形ABCD与四边形A'B'C'D'全等,则∠A'= °,∠A= °,B'C'= ,CD= .?www-2-1-cnjy-com
5.在长为10 m,宽为8 m的长方形空地中,沿平行于长方形各边的方向分割出三个全等的小长方形花圃,其示意图如图所示.求其中一个小长方形花圃的长和宽.【出处:21教育名师】
6.如图,△ABC≌△ADE,∠BAD=35°,∠D=55°,AD与BC交于点D,探究线段AD与BC的位置关系,并说明理由.21·世纪*教育网
培优提升
1.如图,四个图形中是全等图形的是( )
A.①和③ B.②和③ C.②和④ D.③和④
2.如图,△ABD≌△EBC,AB=5,BC=12,则DE的长为( )
A.5 B.6 C.7 D.8
3.如图,在△ABC中,D,E分别是边AC,BC上的点,若△ADB≌△EDB≌△EDC,则∠C的度数为( )2·1·c·n·j·y
A.15° B.20° C.25° D.30°
4.如图是由全等的图形组成的,其中AB=3 cm,CD=2AB,则AF=____________.
5.已知△DEF≌△ABC,AB=AC,且△ABC的周长为22 cm,BC=4 cm,则△DEF中最长的一条边的长为 .2-1-c-n-j-y
6.如图,△ABC≌△DEF,请根据图中提供的信息,写出x= .?
7.如图,△ABC≌△ADE,B点的对应点是D点,若∠BAD=100°,∠CAE=40°,则∠BAC的度数是 .21·cn·jy·com
8.如图,已知△ABF≌△DCE,E与F是对应点.
(1)△DCE可以看成是由△ABF通过怎样的运动得到的?
(2)试问AF,DE的位置关系如何?请说明你的理由.
9.如图,已知△ABC中,AB=AC=10厘米,BC=8厘米,点D为AB的中点,点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上以a厘米/秒的速度由C点向A点运动,设运动的时间为t秒.
(1)求CP的长;
(2)若以C,P,Q为顶点的三角形和以B,D,P为顶点的三角形全等,且∠B和∠C是对应角,求a的值.21世纪教育网版权所有
参考答案
【基础训练】
1.【答案】D
2.【答案】C
解:∵△ABC≌△DEF,∴DE=AB,∵BE=2,AE=1,∴DE=AB=BE+AE=2+1=3.故选C.【版权所有:21教育】
3.【答案】∠A=∠A;∠ADB=∠AEC;CE;AE;AC
4.【答案】120;70;17;8
解:根据全等图形能够完全重合且对应边、对应角分别相等可得出各角的度数.由题意得:∠A'=∠D=120°,∠A=∠D'=70°,B'C'=BC=17,CD=A'B'=8.21教育名师原创作品
5.解:∵三个小长方形全等,
∴它们的长均相等,宽也均相等.
设其中一个小长方形花圃的长为x m,宽为y m,由题图得解得则其中一个小长方形花圃的长和宽分别为4 m和2 m.
6.解:AD⊥BC.
理由如下:∵△ABC≌△ADE,∠D=55°,
∴∠B=∠D=55°,在△AOB中,∠AOB=180°-∠BAD-∠B=180°-35°-55°=90°,∴AD⊥BC.【来源:21cnj*y.co*m】
【培优提升】
1.【答案】C
解:能够完全重合的两个图形叫做全等图形,由此判断即可.
2.【答案】C
解:∵△ABD≌△EBC,AB=5,BC=12,∴BD=BC=12,BE=AB=5,∴DE=BD-BE=12-5=7.故选C.21*cnjy*com
3.【答案】D
解:∵△ADB≌△EDB≌△EDC,∴∠A=∠BED=∠CED,∠ABD=∠EBD=∠C.∵∠BED+∠CED=180°,∴∠A=∠BED=∠CED=90°.在△ABC中,∠C+2∠C+90°=180°,∴∠C=30°.故选D.21cnjy.com
4.【答案】27 cm
解:由全等图形的性质可知:AF=3AB+3CD=3AB+6AB=9AB=27 cm.
5.【答案】9 cm
解:∵△ABC的周长为22 cm,BC=4 cm,
∴AB=AC=×(22-4)=9(cm),∵△DEF≌△ABC,∴△DEF中最长的一条边的长为9 cm.21*cnjy*com
6.【答案】20
解:根据题意得EF=BC=20,即x=20.
7.【答案】70°
解:∵△ABC≌△ADE,
∴∠BAC=∠DAE,
∴∠BAC-∠CAE=∠DAE-∠CAE,
即∠BAE=∠DAC,
∵∠BAD=100°,∠CAE=40°,
∴∠BAE=(∠BAD-∠CAE)=×(100°-40°)=30°,
∴∠BAC=∠BAE+∠CAE=30°+40°=70°.
8.解:(1)△DCE可以看成是由△ABF沿BC方向平移,使F和E重合,然后再绕着E点顺(或逆)时针旋转180°得到的.(答案不唯一)
(2)AF∥DE.
理由:∵△ABF≌△DCE,
∴∠AFB=∠DEC,
∵∠AFB+∠AFE=180°,∠DEF+∠DEC=180°,
∴∠AFE=∠DEF,
∴AF∥DE.
9.解:(1)∵BP=3t厘米,BC=8厘米,
∴CP=(8-3t)厘米;
(2)①当BD=CP时,∵AB=10厘米,D为AB的中点,∴BD=5厘米,
∴5=8-3t,解得t=1,∵△BDP≌△CPQ,∴BP=CQ,即3×1=a×1,解得a=3;
②当BP=CP时,3t=8-3t,解得t=,∵△BDP≌△CQP,∴BD=CQ,即5=a×,解得a=,综上所述,a的值为3或.www.21-cn-jy.com
分析:本题考查了全等三角形的性质,(2)因为对应边不明确,所以要分情况讨论求解.
