7.2.2 垂线 同步练习

7.2.2 垂线
基础训练
1.下列说法正确的是(　　)
A.过一点有无数条直线与已知直线垂直
B.过一点有无数条直线与已知直线相交
C.垂线段就是一条竖直的线段
D.从直线外一点到已知直线的垂线段,叫做这个点到已知直线的距离
2.如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM.若∠AOM=35°,则∠CON的度数为(　　)2·1·c·n·j·y
A.35° B.45° C.55° D.65°
3.如图,AC⊥BC于点C,CD⊥AB于点D,DE⊥AC于点E,则图中垂线段有(　　)
A.5条 B.6条 C.7条 D.8条
4.如图,从书店到公路最近的是___________号路线,其中的数学道理是__________
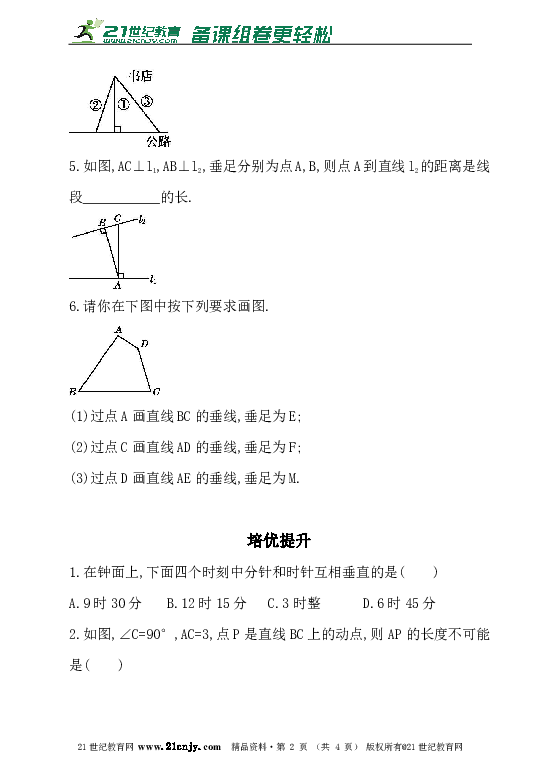
5.如图,AC⊥l1,AB⊥l2,垂足分别为点A,B,则点A到直线l2的距离是线段___________的长.21*cnjy*com
6.请你在下图中按下列要求画图.
(1)过点A画直线BC的垂线,垂足为E;
(2)过点C画直线AD的垂线,垂足为F;
(3)过点D画直线AE的垂线,垂足为M.
培优提升
1.在钟面上,下面四个时刻中分针和时针互相垂直的是(　　)
A.9时30分 B.12时15分 C.3时整 D.6时45分
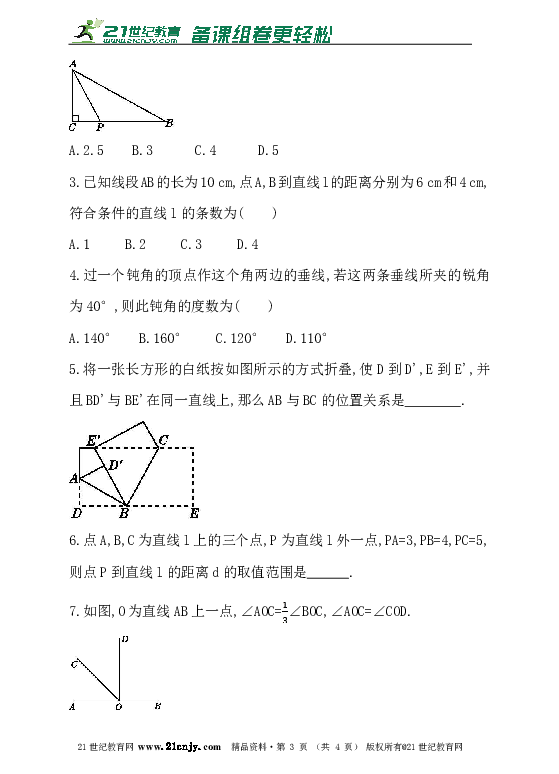
2.如图,∠C=90°,AC=3,点P是直线BC上的动点,则AP的长度不可能是(　　)
A.2.5 B.3 C.4 D.5
3.已知线段AB的长为10 cm,点A,B到直线l的距离分别为6 cm和4 cm,符合条件的直线l的条数为(　　)www-2-1-cnjy-com
A.1 B.2 C.3 D.4
4.过一个钝角的顶点作这个角两边的垂线,若这两条垂线所夹的锐角为40°,则此钝角的度数为(　　)
A.140° B.160° C.120° D.110°
5.将一张长方形的白纸按如图所示的方式折叠,使D到D',E到E',并且BD'与BE'在同一直线上,那么AB与BC的位置关系是________.
6.点A,B,C为直线l上的三个点,P为直线l外一点,PA=3,PB=4,PC=5,则点P到直线l的距离d的取值范围是______.21cnjy.com
7.如图,O为直线AB上一点,∠AOC=∠BOC,∠AOC=∠COD.
(1)求∠COD的度数;
(2)判断OD与AB的位置关系.
8.如图,在小河(河岸为a)的同侧有一个净化水厂A和村庄B,B村的生活用水要到小河中去取,饮用水要到净化水厂A去取.B村的村民怎样走到河边最近?怎样走到净化水厂最近?请你画出图形并说明理由.
9.已知OA⊥OB,垂足为O,∠AOC与∠BOC的度数比为1∶3,求∠AOC的度数.
参考答案
【基础训练】
1.【答案】B　 2.【答案】C
3.【答案】D　
解：本题易漏解,线段CD,CE分别是点C到直线AB,DE的垂线段;线段AD,AE,AC分别是点A到直线CD,DE,BC的垂线段;线段BD,BC分别是点B到直线CD,AC的垂线段;线段DE是点D到直线AC的垂线段.
4.【答案】①;直线外一点与直线上各点连接的所有线段中,垂线段最短
5.【答案】AB
6.解:如图所示.
【培优提升】
1.【答案】C　
解：钟面上相邻两个刻度间的角度是6°,3时整时,分针与时针所成的角为6°×15=90°,所以此时分针与时针互相垂直.21世纪教育网版权所有
2.【答案】A　
解：因为AC是点A到直线BC的垂线段,根据垂线段最短可知,线段AP的长度应该大于或等于线段AC的长度.所以AP的长度不可能是2.【答案】5.21·世纪*教育网
3.【答案】C　
解：遇到未给出图形的几何问题,常要结合题意画出示意图.此题易漏解而错选A或B.要求直线l的条数,画图时要全方位审视问题的条件,找出所有可能的情况,如图所示,l1,l2,l3均符合题意,所以选C.
4.【答案】A　
解：如图所示.∠AOB为已知钝角,OC⊥OB,OD⊥OA,∠COD=40°,易知∠AOC=∠BOD=90°-40°=50°,所以∠AOB=140°.www.21-cn-jy.com
5.【答案】AB⊥BC　
解：由题意知,∠ABD=∠ABD',∠EBC=∠E'BC,所以∠ABD'+∠E'BC=∠ABD+∠EBC=90°.所以AB⊥BC.21·cn·jy·com
6.【答案】0解：由于直线外一点与直线上各点连接的所有线段中,垂线段最短,所以PB,PC一定不是垂线段.
PA可能是点P到直线l的垂线段.所以07.解:(1)因为∠AOC=∠BOC(已知),
且∠AOC+∠BOC=180°(平角定义),
所以∠BOC+∠BOC=180°(等量代换).
所以∠BOC=135°.
所以∠AOC=45°.
又因为∠AOC=∠COD(已知),
所以∠COD=45°(等量代换).
(2)由(1)可知:∠AOC=45°,∠COD=45°,
所以∠AOD=∠AOC+∠COD=90°,
所以OD⊥AB(垂直的定义).
8.解:过B点作BC⊥a,垂足为C,连接AB,如图所示.B村的村民沿BC走到河边最近,理由:直线外一点与直线上各点连接的所有线段中,垂线段最短.B村的村民沿线段BA走到净化水厂A最近,理由:两点之间线段最短.21教育网
分析：本题运用了转化思想.如果把河岸a看作一条直线,把B村和净化水厂A各看作一个点,则到河边最近的问题可转化为垂线段最短问题,到净化水厂最近的问题可转化为两点之间线段最短的问题.
9.解:本题应分为两种情况进行讨论:(1)当射线OC在∠AOB的内部时,如图(1)所示.因为OA⊥OB,所以∠AOB=90°.又因为∠AOC与∠BOC的度数比为1∶3,所以∠AOC=90°×=22.5°.【来源：21·世纪·教育·网】
(2)当射线OC在∠AOB的外部时,如图(2)所示.因为OA⊥OB,所以∠AOB=90°.又因为∠AOC与∠BOC的度数比为1∶3,所以∠AOC与∠AOB的度数比为1∶2,所以∠AOC=90°×=45°.2-1-c-n-j-y
综上可知,∠AOC的度数为22.5°或45°.